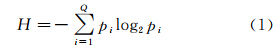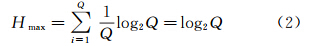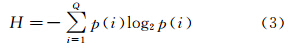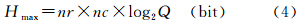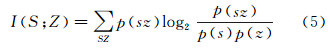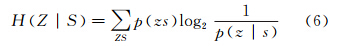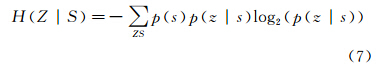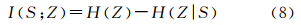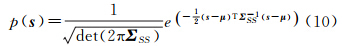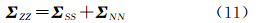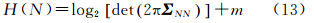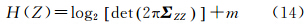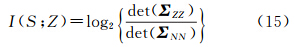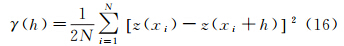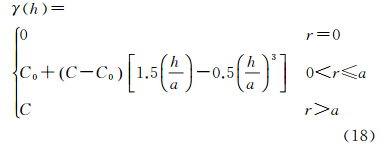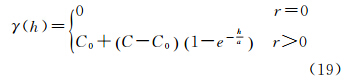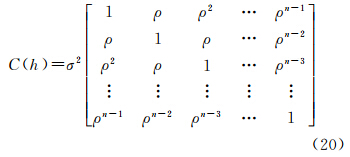1 引 言
在社会进步乃至日常生活中,遥感和地理信息系统(GIS)的作用日益凸显。然而,目前对于多源空间数据信息量的研究偏少,远没有达到以米计长度、以千克论质量、以安培量电流的定量程度[1],这与空间信息的重要地位极不相称。
估算与分析遥感影像的信息量是定量遥感的基础性工作,并有诸多应用:首先,作为综合指标,信息计量通常须考虑影像分辨率、信噪比、量测精度等因素,因而比传统的单一性指标(如分辨率等)更准确地度量其“信息”量而不是“数据”量,从而成为合理确定信息产业价格的重要参考指标;其次,信息熵量化了数据可压缩的极限,可用于指导数据压缩,更好地辨别、利用不同的压缩方法对于不同数据的适用性;另外,还可用于改善遥感影像处理方法,确定影像处理方法的性能,以提高处理方法的可靠性和效率。
经典信息论中[2],信息是可量测的数量,反映接受者从多个符号串辨识某一串符号的能力。作为对地面信息的记录,遥感影像获取、处理、存储和分发过程中,始终伴随着信息的传递和信息量的增减,因此,使用信息科学基础理论之一的信息论进行遥感影像信息量的度量和遥感影像质量的评价是适当的[3]。影像信息量的测度和指标包括空间分辨率、辐射分辨率、不同目标类型间的辐射对比度、所获取影像的最终应用等[4]。现有的影像信息度量的方法有的直接利用信息熵作为评价信息量的标准[5, 6],例如,文献[7]在处理遥感分类问题中,提出了基于信息熵的最优空间尺度选择方法;文献[8]在影像融合处理中,通过计算信息熵来确定遥感数据的最佳波段组合。
遥感影像的信息量取决于灰度量化等级、灰度噪声、空间分辨率、几何变形、邻元相关性、波段间相关性等因素[1]。现有研究中,学者们通常会分别考虑影响影像信息量的这些因素,并分别将其纳入信息量的计算中,例如,文献[9]讨论了信息量与信噪比的关系;文献[10]讨论了分辨率对信息量的影响;文献[11,12]讨论了相邻像元间相关性对信息量的影响。然而,这些影响因素之间存在相关性,简单地分别计算分析将导致结果欠精准,因为它们的综合影响不是单因素影响的简单相加,故不能单纯地将其分开来进行计算。
地统计学中的变异函数,也称为变差函数,可用来度量影像中的空间变异性。由传感器获得的度量结果(即数据)可理解为区域化变量的实现,故可以用变异函数来度量遥感影像的空间结构[13, 14]。变异函数可以描述某像素与其邻域的空间依赖关系,将半方差与空间间隔联系起来,提供了空间变异性的尺度和模式的无偏估计[15]。
本文采用信息论与地统计的方法,综合考虑邻元相关性和噪声等因素的影响,提出了遥感影像信息量上界的计算方法,并进行了试验验证。
2 方 法
2.1 信息熵与影像信息量
信息是个相当宽泛的概念,很难用一个简单的定义将其完全准确地把握。然而,对于任何一个概率分布,可以定义一个称为熵(entropy)的量,它的许多特性符合度量信息的直观要求[16, 17]。熵是随机变量的不确定性的一个度量,设有Q个可能的消息,其相应的概率分别为p1,p2,…,pQ,于是,平均信息量可用熵H进行计算,即
从熵的性质可知,当每个消息概率均为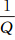 时,H有最大值,故最大的可能平均信息量为
时,H有最大值,故最大的可能平均信息量为
可以将这些概念应用到遥感影像上[18]。遥感影像的信息熵能够较好地反映遥感影像所表达信息的多少,它与遥感影像的灰度变化程度直接相关,信息熵就是遥感影像无序程度的度量[19]。设每一个像元的灰度级为一个消息,则一幅经过数字转换的数字图像可以看作为一组消息。假设一幅nr×nc的数字影像有Q个灰度级,p(i)表示第i级灰度值出现的概率,可近似地由灰度频率fi计算得到: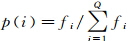 。则影像的熵(单像素)为
。则影像的熵(单像素)为
而此数字图像中总的信息量最多可达到(当每一灰度级等概出现时)
这个概念可以推广到互信息。互信息是在给定另一随机变量知识的条件下,原随机变量不确定度的缩减量[16]。考虑两个随机变量S和Z,它们的联合概率密度函数为p(sz),其边际概率密度函数分别为p(s)和p(z),将互信息定义为
互信息用来度量一个随机变量包含另一个随机变量的信息量,而熵恰好变成一个随机变量的自信息[16],同时,熵是平均不肯定性的定量描述,而熵差才是接收端获得的信息量,因此互信息是比熵更有意义的物理量[20]。
若信道不存在噪声,信道输出符号与输入符号将一一对应,于是接收到传递过来的符号后就能消除对发送信号的先验不肯定性。但实际的信道中总存在着噪声,它会导致接收到符号Z后对发送的符号仍有不肯定性,于是引入条件熵的概念,定义为
因而对于条件熵进一步推导可得
式中,S表示原始影像(即信号);N表示噪声。根据式(5)—式(7),容易推出信息熵、互信息、条件熵的关系,即因而,互信息I(S;Z)是在Z给定知识的条件下S的不确定度的缩减量。
在光学遥感系统中,附加在数据Z中的噪声N被认为是独立于信号的,并且是加性噪声[21],表示为Z=S+N。加性噪声即由发生源产生并叠加在图像信号上且与图像信号无关的噪声,通常可以由正态分布(高斯分布)表示为均值为零的随机过程,其概率密度函数可表示为
式中,ΣNN表示噪声N的协方差矩阵;det(ΣNN)表示噪声N的协方差矩阵的行列式。若假设影像信号亦服从正态分布,则影像概率密度函数为
式中,ΣSS表示信号S的协方差矩阵;det(ΣSS)表示S的协方差矩阵的行列式;μ为S的均值向量。由于影像与噪声相互独立,故数据Z的协方差为S与N的协方差之和为根据互信息的计算式(8)可得在加性噪声条件下的互信息为
本文参照文献[9]中对于信息量计算的结论,首先对H(N)进行推导,则有
式中,m表示自由度,即样本中独立或能自由变化的数据的个数。若假设Z服从正态分布,对H(Z)可以进行类比推导,H(Z)可表示为故影像的信息量(影像Z传递的关于信号S(即地表分布)的互信息)为
若Z的正态分布假设不成立,式(14)依然可以用于计算影像Z的信息熵的上限,因为同方差的随机分布中,正态分布的信息熵最大。因此,式(15)可用于影像的信息含量的上限值,或者视为影像Z作为传输信号S的信道的容量。
因而,计算影像信息量的问题转化为对于影像协方差矩阵和噪声协方差矩阵的计算问题。基于此考虑,由于地统计学中的变异函数可用来分析影像空间结构特征,量化特定影像的空间相关性,故有效解决协方差矩阵的计算问题,从而进行影像信息量的计算。
2.2 变异函数模型与影像的空间协方差
在地统计学中,变异函数是研究中非常重要的工具,它用来表示区域内区域化变量的相关关系和空间结构。对于遥感影像,变异函数可表示为[22, 23]
式中,z(xi)表示像素xi的灰度值;h表示距离间隔;N为点对个数。变异函数与像素xi的位置无关,只依赖于两个像素点之间的距离,因而变异函数可以测量间距为h时两个像素间的相关性与差异性。通常情况下,距离相近的点要比远离的点关系更为密切,像素间间距越大,其变异性越大,相似性越小。为了表征区域化变量在一定尺度上的空间变异和相关程度,通常有3个重要的参数:基台值、变程、块金值。基台值表示变异函数随着间距递增到一定程度时出现的平稳值,代表由于样本数据中存在空间相关性而引起的方差变化范围。变程是变异函数达到基台值时的样本间距,在变程距离范围内,样本点之间具有相关性,因此,在此范围内的插值才是有意义的。理论上当h=0时,变异函数的值应该等于0。但由于噪声等因素的影响,通常会使得在h很小时,变量值之间仍然存在差异,因而有了块金值的概念。本文中主要用块金值来衡量噪声的影响[24],它表示区域化变量在小于观测尺度时的非连续变异,此时的变异性在空间不存在相关关系。当h→0时,变异函数为
式中,σ2n为噪声方差;C0为块金值。因而在得到块金值后,即可对噪声方差进行评估,从而得到噪声的协方差矩阵,即式(15)中的分母部分。在地统计方法中,利用数学模型对已有的变异函数进行拟合是非常必要的[25, 26],因为本文不仅需要利用到块金值,同时还需要利用拟合后的模型的参数进行协方差函数的计算。本文主要用到球状模型和指数模型,因为这两个模型在所选定的拟合策略中,拟合效果是最好的。球状模型定义为
指数模型定义为
式中,C0为块金值;C为基台值;a为变程。协方差函数C(h)也可描述空间的变异性,遥感影像灰度具有一阶马尔科夫过程的统计特征,其协方差阵可描述为[1]
式中,σ2为影像方差;p为相邻像元间的自相关系数。地统计学中,协方差函数与变异函数的关系可表示为 式中,C(0)为区域化变量的方差,对于遥感影像来说,C(0)就是影像的方差。在得到拟合后的模型参数后,根据协方差函数所需的要素,即可得到此影像的协方差函数,从而有效地解决了式(15)中分子部分协方差矩阵的问题,因而使得影像信息量的问题迎刃而解。3 实例分析 3.1 试验区域和数据
试验区域位于湖北省武汉市,采用美国陆地探测卫星系统LandsatTM获取的影像,轨道号为P123R39,获取时间是2009年3月14日,影像被裁剪成200像素×200像素的大小,由于不同地物类型对于影像的信息量影响较大,故本文分别对城市、农田、山地3种不同的地物类型进行信息量的计算,如图 1所示。
 |
| 图 1 Landsat TM 影像 Fig. 1 Landsat TM images representing different land cover types |
Landsat TM影像的1—5波段和7波段参与影像信息量的计算,首先分别求取不同波段影像对应的变异函数,根据变异函数的具体性状选择合适的拟合模型对其进行拟合,得到相应的模型参数。根据变异函数与协方差矩阵的关系,分别得到影像的协方差矩阵和噪声的矩阵,从而得到影像的信息量。
3.3 试验结果分析
图 2分别描述波段1—5和波段7中,城市、农田、山地3种典型地物的变异函数曲线,本文根据点对数目作为权系数、最小二乘意义下进行加权拟合的策略,确定采用的拟合模型是套合结构,即结合块金模型时,指数模型或球状模型的自由组合结构。对于同一种地物类型,不同波段的变异函数曲线的变化性状是相似的,差别在于纵坐标的变化很大。综合3种地物类型来看,波段1—3变异函数的纵坐标偏小,波段4、波段5、波段7变异函数的纵坐标明显增加。当横坐标达到变程时,变异函数的纵坐标会相应增加到基值,并基本达到平稳状态,此时纵坐标的大小反映了影像方差的大小情况。图 2(a)—(f)中,城市的变异函数曲线的纵坐标值明显大于其他两种地物类型,其中第5波段城市影像的方差是最大的。图 2(d)中,农田的变异函数曲线的纵坐标明显大于其他两种地物类型,此波段农田影像的方差是最大的。由于变异函数在原点处的性状可以反映区域化变量的空间连续性,从图 2可以看出,城市的变异函数曲线变异程度增加得最快,农田和山地变化较缓慢,其中山地的空间连续性略优于农田,而城市的空间连续性最差,而这是由它们各自的空间结构和纹理特征决定的。根据拟合后的变异函数,可以得到拟合后套合模型的参数,用于进行协方差函数的计算。协方差函数的构成同样是由块金值、基值和变程3个因素决定,3种不同地物类型在模型的选择上,除了均含有块金模型外,对于城市本文选择指数模型与球状模型的组合,农田选择两个指数模型的组合,山地选择两个球状模型的组合,具体参数如表 1、表 2、表 3所示。
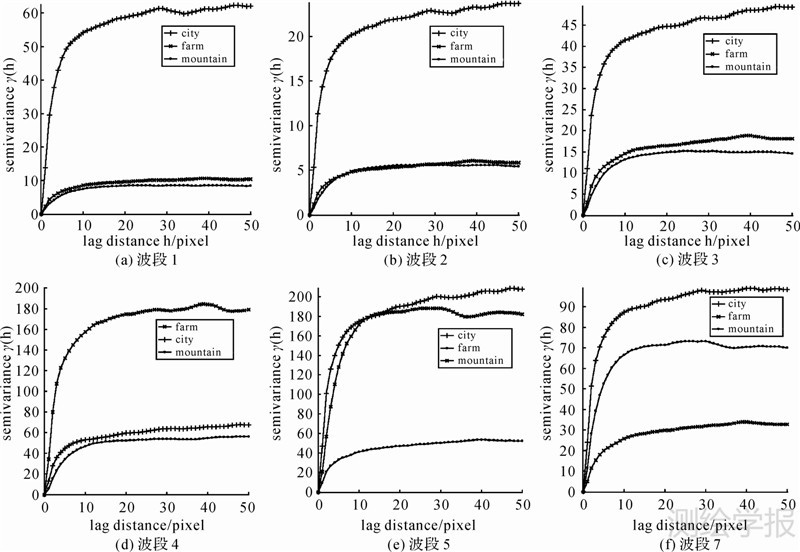 |
| 图 2 3种地物类型的变异函数曲线 Fig. 2 Variograms estimated from three different land cover types |
| 波段 | 块金模型 | 指数模型 | 球状模型 | ||
| 块金值 | 基台值 | 变程 | 基台值 | 变程 | |
| 1 | 0.28 | 26.16 | 25.01 | 35.32 | 4.46 |
| 2 | 0.45 | 8.82 | 33.73 | 14.21 | 4.61 |
| 3 | 0.14 | 17.01 | 48.20 | 31.06 | 4.85 |
| 4 | 0.25 | 46.41 | 7.40 | 26.13 | 90.12 |
| 5 | 0.18 | 155.41 | 6.81 | 59.29 | 72.81 |
| 7 | 0.17 | 40.44 | 5.18 | 47.96 | 19.22 |
| 波段 | 块金模型 | 指数模型 | 球状模型 | ||
| 块金值 | 基台值 | 变程 | 基台值 | 变程 | |
| 1 | 0.39 | 7.51 | 9.30 | 2.52 | 39.32 |
| 2 | 0.31 | 4.10 | 9.23 | 1.54 | 44.31 |
| 3 | 0.12 | 10.38 | 33.63 | 8.01 | 4.87 |
| 4 | 0.35 | 96.07 | 20.95 | 71.89 | 5.01 |
| 5 | 0.57 | 30.85 | 7.24 | 23.79 | 51.67 |
| 7 | 0.21 | 19.20 | 8.91 | 14.95 | 46.06 |
| 波段 | 块金模型 | 指数模型 | 球状模型 | ||
| 块金值 | 基台值 | 变程 | 基台值 | 变程 | |
| 1 | 0.23 | 4.36 | 6.88 | 3.51 | 22.12 |
| 2 | 0.11 | 2.95 | 6.92 | 2.55 | 19.67 |
| 3 | 0.15 | 8.56 | 7.10 | 6.30 | 20.12 |
| 4 | 0.63 | 28.05 | 24.29 | 26.94 | 8.54 |
| 5 | 0.96 | 85.60 | 15.24 | 95.63 | 6.94 |
| 7 | 0.35 | 38.42 | 5.40 | 32.97 | 15.08 |
根据协方差函数,可以得到3种不同地物类型影像的信息量。为了进一步说明相邻像元间的相关性给信息量带来的冗余,笔者分别计算了未考虑相关性和顾及相关性两种情况下的影像的信息量,如表 4、表 5所示。在这两种情况下,不同类型的地物的信息量均表现出很大差别,这也是本文针对不同地物类型分别进行影像信息量计算的原因。其中,从不同波段的角度来看,城市的信息量普遍大于农田和山地,而农田和山地的信息量有微小差别。城市和山地在第5波段的信息量最大,农田在第4波段的信息量最大。综合所有波段来看,城市的总信息量最大,农田和山地的总信息量较相似。试验结果表明,顾及影像空间相关性后的信息量度量结果较未考虑空间相关性的结果偏小,因为前者计算时扣除了相关性导致的冗余信息,结果更客观、准确,且能说明不同地物类型的地学特征。图 3更直观地展现了3种地物类型的信息量,城市所包含的大量信息量更加明显,这亦符合人们对于这3种地物类型的信息量的直观理解,由于城市这种地物类型纹理较细,变化较快,所以信息量会明显大于农田和山体这类纹理比较规则、变化比较慢的地物类型。
| 波段1 | 波段2 | 波段3 | 波段4 | 波段5 | 波段7 | 总信息量 | |
| 城市 | 4.91 | 3.46 | 4.56 | 5.13 | 6.88 | 5.85 | 30.78 |
| 农田 | 3.18 | 2.70 | 3.70 | 6.50 | 4.65 | 3.90 | 24.63 |
| 山地 | 3.06 | 2.48 | 3.98 | 4.45 | 6.15 | 4.83 | 24.96 |
| 波段1 | 波段2 | 波段3 | 波段4 | 波段5 | 波段7 | 总信息量 | |
| 城市 | 4.25/td> | 2.79 | 3.88 | 4.34 | 6.18 | 5.22 | 26.66 |
| 农田 | 2.50 | 1.96 | 2.86 | 5.74 | 3.86 | 3.00 | 19.94 |
| 山地 | 2.29 | 1.52 | 2.96 | 3.29 | 5.04 | 3.95 | 19.05 |
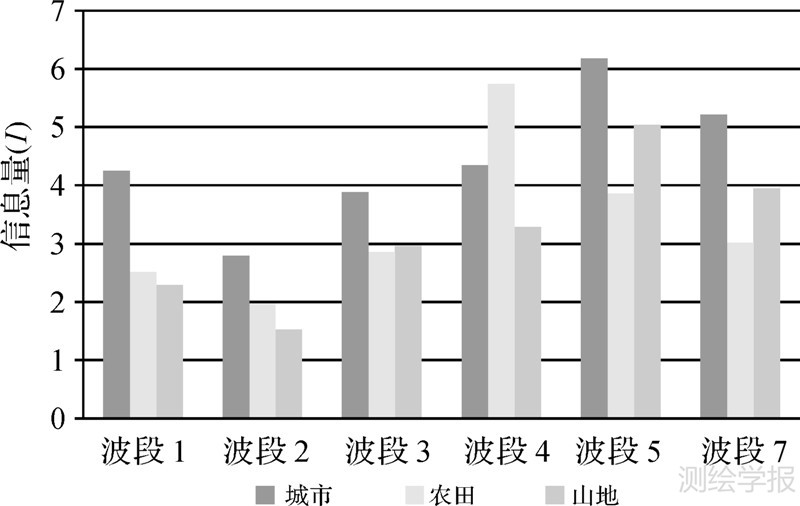 |
| 图 3 3种地物类型不同波段的信息量 Fig. 3 Information content estimated by three different land cover types in different bands |
对于影像的信息量大小与方差的关系,文献[9]已对其进行研究。其研究是在不考虑影像相关性的情况下,证明了影像的信息量与噪声存在正相关关系。而笔者更关心的问题在于利用式(15)后与仅利用式(1)的区别,即考虑空间相关性的基础上,如何解决影像信息量的度量问题。为了探寻其内在联系,基于Blacknell的理论基础,本文对影像信息量与方差的关系进行了拟合分析,如图 4所示,3种不同地物分别进行对数拟合的拟合度均大于90%,因而可以推断影像信息量与方差存在对数正相关关系,而不是完全独立的。基于此,笔者对影像信息量与方差的对数的关系进行进一步明确,如图 5所示,故结合表 1可以解释不同地物信息量的大小不同的原因。同时,根据拟合公式的系数可知,随着方差的增加,城市的信息量增加得最快,农田其次,而山地的信息量增加得最慢。
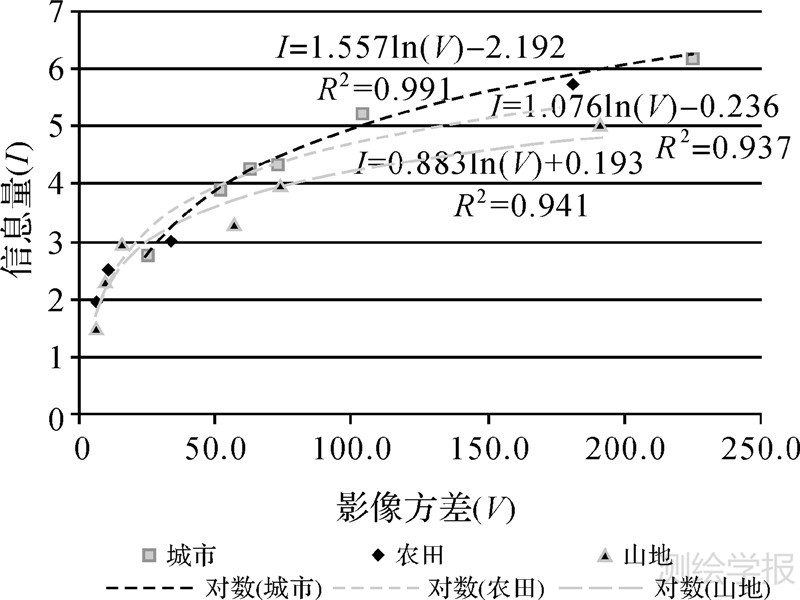 |
| 图 4 3种地物类型影像信息量与方差的关系图 Fig. 4 Relation between information content and variance for three different land cover types |
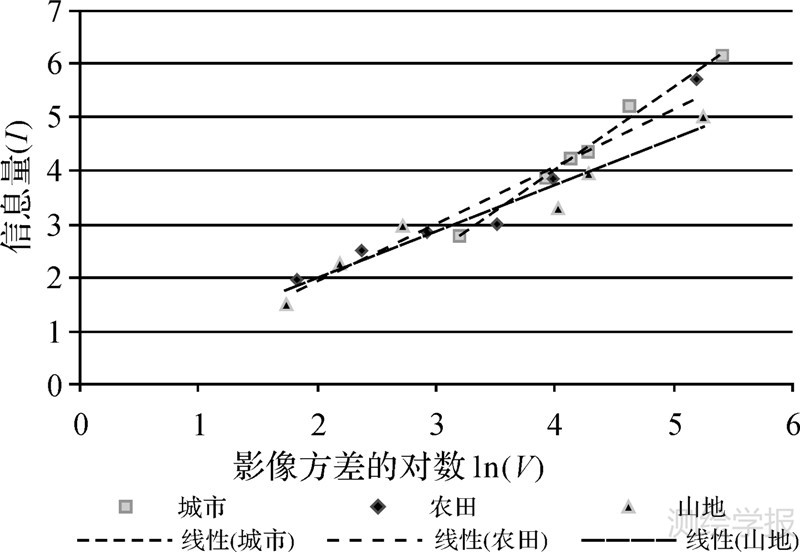 |
| 图 5 3种不同地物类型影像信息量与方差对数的关系图 Fig. 5 Relation between information content and logarithm of variance for three different land cover types |
本文采用了不同的拟合方法对影像的信息量进行拟合,如表 6所示,从各种拟合方法的拟合公式可以推断,影像方差与信息量确实存在着正相关关系。从可决系数可知,对数拟合的拟合效果在城市和山地这两种地物类型中明显优于其他拟合方法。对于农田来说,乘幂拟合的拟合效果略优于对数拟合,而对数拟合的效果优于其他两种拟合方法。根据本文所采用的数据,综合3种不同的地物类型,笔者认为可以推断影像方差与信息量存在对数正相关关系,而是否不同地物类型会导致方差与信息量存在不同的正相关关系,仍需大量数据进行探讨。
| 拟合方法 | 城市 | 农田 | 山地 | |
| 线性拟合 | 拟合公式 | I=0.015V+3.087 | I=0.020V+2.326 | I=0.016V+2.236 |
| 可决系数 | R=2=0.861 | R=2=0.943 | R=2=0.835 | |
| 对数拟合 | 拟合公式 | I=1.557ln(V)-2.192 | I=1.076ln(V)-0.236 | I=0.883ln(V)+0.193 |
| 可决系数 | R=2=0.991 | R=2=0.937 | R=2=0.941 | |
| 乘幂拟合 | 拟合公式 | I=0.928V0.360 | I=1.143V0.305 | I=1.096V0.294 |
| 可决系数 | R=2=0.973 | R=2=0.976 | R=2=0.902 | |
| 指数拟合 | 拟合公式 | I=3.201e0.003V | I=2.408e0.005V | I=2.220e0.005V |
| 可决系数 | R=2=0.763 | R=2=0.845 | R=2=0.680 |
本文提出了基于加性噪声环境的多光谱遥感影像的信息度量方法,以期解决考虑了噪声和空间相关性等影响遥感影像信息量的因素的不同地物类型的影像信息量。试验表明,城市含有最大的信息量,同时影像的信息量与影像方差呈对数正相关关系。考虑到城市含有道路、房屋等多种类型的复杂结构,而农田、山地的空间结构相对简单规则,因此随着方差的增加,农田和山地的信息量增加相对较慢。于是,可从遥感影像的信息论特性,解释遥感影像所要表达的信息的内涵,这也正是本文想要探讨影像信息量问题的原因。遥感影像信息量的计量,对于定量评价影像的质量起到关键作用,它使得用户在利用影像之前,对于影像的信息具有客观的认知。
致谢:感谢美国加州大学圣芭芭拉分校地理系的Phaedon Kyriakidis教授为本文提供理论指导。
| [1] | LIN Zongjian, ZHANG Yonghong. Measurement of Information and Uncertainty of Remote Sensing and GIS Data[J]. Geomatics and Information Science of Wuhan University, 2006, 31(7): 569-572. (林宗坚, 张永红. 遥感与地理信息系统数据的信息量及不确定性[J]. 武汉大学学报: 信息科学版, 2006, 31(7): 569-572.) |
| [2] | SHANNON C E. A Mathematical Theory of Communication[J]. Bell System Technical Journal, 1948, 27(3): 379-423. |
| [3] | WANG Zhanhong. A Research on the Metric Model for Remote Sensing Entropy and Quality[D]. Wuhan: Wuhan University, 2004. (王占宏. 遥感影像信息量及质量度量模型的研究[D]. 武汉: 武汉大学, 2004.) |
| [4] | NARAYANAN R M, PONNAPPAN S K, REICHENBACH S E. Effects of Uncorrelated and Correlated Noise on Image Information Content[J]. Geoscience and Remote Sensing Symposium, 2001, 4(7): 1898-1900. |
| [5] | CHEN Yan. Information-Theoretic Research on Information Contents in Remotely Sensed Images[D]. Wuhan; Wuhan University, 2010. (陈艳. 基于信息理论的遥感图像信息度量[D]. 武汉: 武汉大学, 2010.) |
| [6] | LIU Yanfang, LAN Zeying, LIU Yang, et al. Multi-scale Evaluation Method for Uncertainty of Remote Sensing Classification Based on Hybrid Entropy Model[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 82-87. (刘艳芳, 兰泽英, 刘洋, 等. 基于混合熵模型的遥感分类不确定性的多尺度评价方法研究[J]. 测绘学报, 2009, 38(1): 82-87.) |
| [7] | HAN Peng, GONG Jianya, LI Zhilin. A New Approach for Choice of Optimal Spatial Scale in Image Classification Based on Entropy[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 676-679. (韩鹏, 龚健雅, 李志林. 基于信息熵的遥感分类最优空间尺度选择方法[J]. 武汉大学学报: 信息科学版, 2008, 33(7): 676-679.) |
| [8] | XU Han, YAN Qin, XU Banlin, et al. The Best Band Selection and Quality Assessment of Multisource Remote Sensing Image Fusion[J]. Science of Surveying and Mapping, 2007, 32(3): 72-74. (许菡, 燕琴, 徐泮林, 等. 多源遥感影像融合最佳波段选择及质量评价研究[J]. 测绘科学, 2007, 32(3): 72-74.) |
| [9] | BLACKNELL D, OLIVER C J. Information Content of Coherent Images[J]. Journal of Physics D: Applied Physics, 1993, 26(9): 1364-1370. |
| [10] | NARAYANAN R M, DESETTY M K, REICHENBACH S E. Effect of Spatial Resolution on Information Content Characterization in Remote Sensing Imagery Based on Classification Accuracy[J]. International Journal of Remote Sensing, 2002, 23(3): 537-553. |
| [11] | AIAZZI B, BARONTI S, SANTURRI L, et al. Information-Theoretic Assessment of Multi-dimensional Signals[J]. Signal Processing, 2005, 85(5): 903-916. |
| [12] | RAZLIGHI Q R, KEHTARNAVAZ N, NOSRATINIA A. Computation of Image Spatial Entropy Using Quadrilateral Markov Random Field[J].IEEE Transactions on Image Processing, 2009, 18(12): 2629-2639. |
| [13] | WOODCOCK C E, STRAHLER A H, JUPP D L B. The Use of Variograms in Remote Sensing: I. Scene Models and Simulated Images[J]. Remote Sensing of Environment, 1988, 25(3): 323-348. |
| [14] | WOODCOCK C E, STRAHLER A H, JUPP D L B. The Use of Variograms in Remote Sensing: II. Real Digital Images[J]. Remote Sensing of Environment, 1988, 25(3): 349-379. |
| [15] | CURRAN P J. The Semivariogram in Remote Sensing—An Introduction[J]. Remote Sensing of Environment, 1988, 24(3): 493-507. |
| [16] | COVER T M, THOMAS J A. Elements of Information Theory[M]. 2nd ed.New York: John Wiley & Sons Inc., 2006. |
| [17] | FU Zuyun. Information Theory—Basic Theory and Application[M]. Beijing: Publishing House of Electronics Industry, 2001. (傅祖芸. 信息论——基础理论与应用[M]. 北京: 电子工业出版社, 2001.) |
| [18] | ZHANG Renlin. Penetration of Information Theory to Science of Surveying and Mapping[J]. Science of Surveying and Mapping, 1994(2): 28-31. (张仁霖. 信息论向测绘科学的渗透[J]. 测绘科学, 1994(2): 28-31.) |
| [19] | CHENG Jicheng, GUO Huadong, SHI Wenzhong, et al. The Undetermined Questions of Remote Sensing Data[M]. Beijing: Science Press, 2004. (承继成, 郭华东, 史文中, 等. 遥感数据的不确定性问题[M]. 北京: 科学出版社, 2004.) |
| [20] | TAO Chunkan, TAO Chunkuang. Optical Information Theory[M]. Beijing: Science Press, 2004. (陶纯堪, 陶纯匡. 光学信息论[M]. 北京: 科学出版社, 2004.) |
| [21] | CORNER B R, NARAYANAN R M, REICHENBACH S E. Noise Estimation in Remote Sensing Imagery Using Data Masking[J]. International Journal of Remote Sensing, 2003, 24(4): 689-702. |
| [22] | VANDER MEER F. Remote-sensing Image Analysis and Geostatistics[J]. International Journal of Remote Sensing, 2012, 33(18): 5644-5676. |
| [23] | ASMAT A, ATKINSON P M, FOODY G M. Geostatistically Estimated Image Noise is a Function of Variance in the Underlying Signal[J]. International Journal of Remote Sensing, 2010, 31(4): 1009-1025. |
| [24] | CURRANP J, DUNGAN J L. Estimation of Signal-to-Noise:A New Procedure Applied to AVIRIS Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1989, 27(5): 620-628. |
| [25] | CRESSIE N. Fitting Variogram Models by Weighted Least Squares[J]. Journal of the International Association for Mathematical Geology, 1985, 17(5): 563-586. |
| [26] | GRINGARTEN E, DEUTSCH C V. Variogram Interpretation and Modeling[J]. Mathematical Geology, 2001, 33(4): 507-534." |