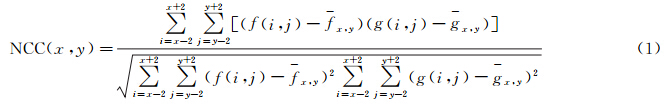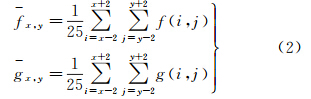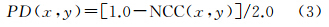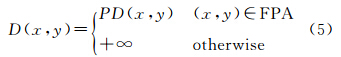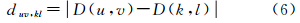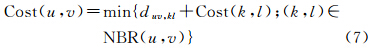2. 地球空间信息技术协同创新中心,湖北 武汉 430079;
3. 国家测绘地理信息局卫星测绘应用中心,北京 100830;
4. 浙江省地理信息中心,浙江 杭州 310012
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 100830, China;
4. Geomatics Center of Zhejiang Province, Hangzhou 310012, China
1 引 言
数字正射影像(DOM)作为国家空间基础设施的重要组成部分,是摄影测量与遥感基本数据产品-4D产品(DOM、DRG、DLG和DEM)的重要组成部分。正射影像镶嵌作为DOM生产的最后一个环节,其中接缝线选择与优化在数据生产过程中的很多情况下仍然需要辅以人工编辑,国内外关于这方面的研究工作一直没有间断[1, 2, 3]。文献[4]在差值影像上逐行确定接缝点搜索最优接缝线,但其基于单个像素的差异很难表达真实的投影差;文献[5, 6]利用GRASP算法进行镶嵌线的选择;文献[7]在待镶嵌影像重叠区使用立体匹配算法选择联结点,然后使用最短路径算法连接这些联结点形成接缝线,但其接缝线的质量依赖于匹配算法的可靠性;文献[8]分别将色彩、纹理及与重叠区垂直平分线的距离设计成蛇模型的两个内部能量和一个外部能量,然后初始化两条初始蛇线,通过蛇模型的演化得到最后优化的接缝线,但其得到的接缝线可能会收敛于局部最小值;文献[9, 10]提出基于蚁群算法的接缝线优化方法,但其接缝线优化质量受蚂蚁数量影响较大;文献[11]提出了一种形态学的方法,即尽量使接缝线沿着明显地物的边界行进,从而用地物的边界来掩盖接缝线两边地物的几何及辐射差异,但其生成接缝线质量依赖于分类边界的精确程度;文献[12]通过归一化相关系数衡量差异,然后通过一种迭代搜索的Dijkstra算法得到最小化的最大差异值,并将差异值大于此值的像素归并到禁止穿越区域,最后通过Dijkstra算法得到最终的优化接缝线;文献[13]在文献[12]的基础上,采用贪心法取代Dijkstra算法进行局部路径选择并改进了算法判定条件,但此类方法基于5×5局部区域对差异进行表达,很难完全反映建筑物等大投影差地物的真实差异;文献[1, 14, 15, 16, 17, 18, 19, 20]利用现有辅助数据(如DSM数据[1]、LiDAR数据[14, 15, 16, 17]及道路矢量数据[18, 19, 20])确定接缝线优先穿越区域或者禁止穿越区域,让接缝线行进在道路或者避免穿越建筑物,从而达到优化接缝线的目的,但此类方法需要辅助数据的支持;文献[21]提出一种基于均值漂移分割的接缝线优化方法,其算法使用重叠区分割后对象最小外接矩形的长作为阈值选择优先穿越区域,然后通过设置优先穿越区域中像素差异的权值,让最终的接缝线尽量行进在优先穿越区域中,但此算法效率较低。
传统方法大多基于单个像素或某个固定窗口大小的局部区域对重叠区差异进行表达,很难完全反映建筑物等大投影差地物的真实差异。本文旨在通过影像分割对重叠区差异表达进行改进。影像分割可以得到同质区域,统计同质区域中大差异像素所占区域像素总数的比例,并将其比例作为此区域的差异值,然后选择低差异值的区域作为接缝线优先穿越区域,从而尽量避免接缝线穿越投影差异大的区域。考虑到分割算法的效率,本文提出一种自适应标记分水岭分割的方法对接缝线进行优化。此方法首先通过对重叠区自适应标记分水岭分割所得区域的差异进行衡量,从而确定优先穿越区域,最后,在优先穿越区域中采用基于最小二叉堆的Dijktra算法进行接缝线优化。
2 原理及方法
在正射纠正的过程中,由于建筑物等地物不包括在DEM中,这些区域在正射纠正中没有得到正确的平面位置,形成了投影差[13]。由于左右影像拍摄的视角不同,其投影差也不一样,在左右影像上形成较大的差异,接缝线优化就是要使接缝线避免穿越这些差异较大的区域,所以接缝线优化包括两个关键的步骤:①重叠区差异表达;②路径搜索。重叠区差异表达是路径搜索的基础和前提,差异表达的效果直接影响优化后接缝线的质量。为了更好地对重叠区差异进行表达,本文将图像分割引入接缝线优化中。
本文提出的接缝线优化方法流程图如图 1所示,首先对左右影像重叠区进行自适应标记分水岭分割,然后分别计算左右影像每个区域的区域差异,接着分别在左右影像建立区域邻接矩阵,在此基础上分别确定左右影像的优先穿越区域,然后将左右影像的优先穿越区域进行求交处理,求出最终的优先穿越区域,最后在最终的优先穿越区域中基于最小二叉堆的Dijkstra最短路径算法得到最终优化的接缝线。
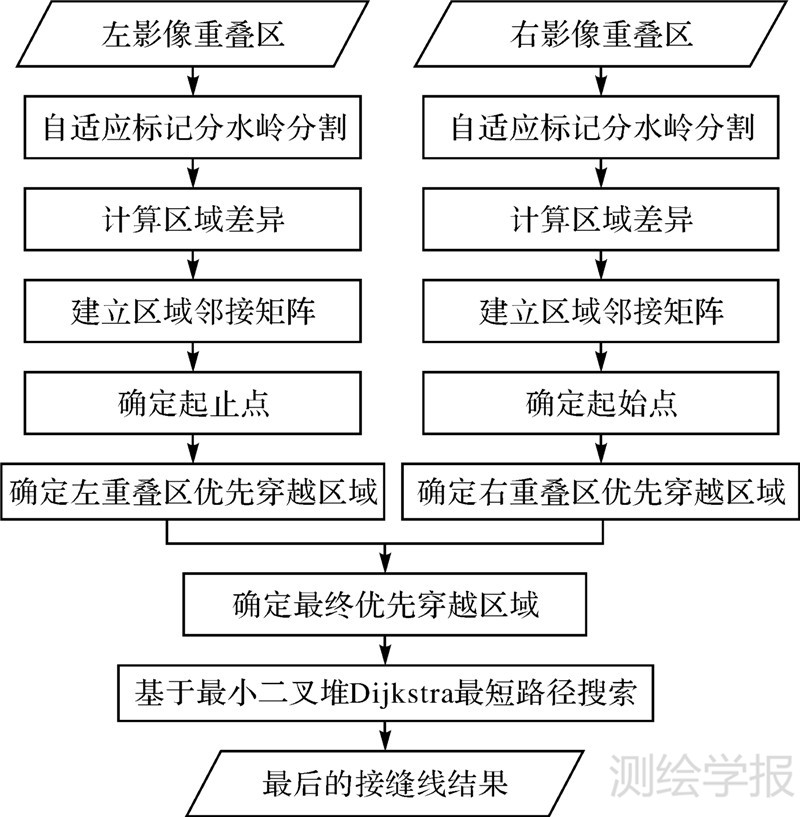 |
| 图 1 本文提出的接缝线优化方法流程图 Fig. 1 The flow of the proposed seamline optimization method |
分水岭分割是将图像想象成一个三维的空间,其中两维为图像的两个坐标,另一维为图像的灰度值。其基本思想如下:假设在每个区域最小值的位置上打一个小孔,让水以均匀的上升速率从小孔中涌出,从低到高淹没整个地形。当处在不同汇聚盆地中的水将要聚合在一起时,修建的大坝将阻止聚合。水将只能到达大坝的顶部处于水线之上的程度,这些大坝的边界对应于分水岭的分割线。分水岭算法通常会由于噪声和其他诸如梯度的局部不规则性的影响造成过度分割。一种用于控制过度分割的方法是以标记的概念为基础的,即标记分水岭算法。一个标记是属于一幅图像的连通分量,有与重要对象相联系的内部标记,还有与背景相联系的外部标记[22, 23, 24]。本文采取文献[25, 26]中的区域自适应的分水岭分割算法,此算法分为以下3个步骤。
(1) 区域自适应标记提取。首先采取Sobel算子提取梯度影像,对原始梯度影像进行梯度直方图统计,然后设置阈值α提取标记图像,由于单一的阈值难以满足不同区域分割的要求,对梯度图像进行高斯低通滤波去除高频信息,估计影像梯度的局部分布情况,用于调整分割阈值,即用一个尺度参数T乘以低通滤波后的梯度影像来调整分割阈值,从而得到最终的标记。
(2) 伪标记区域剔除。将备选标记像素进行聚类,剔除面积小于给定阈值A的伪标记区域。
(3) 快速标记分割。采用Meyer标记分水岭分割方法对待分割像素进行标记分割,得到最终分割结果[25, 26]。
该算法较好地解决了分水岭分割算法过分割的问题,能够很好地适应遥感影像复杂的地物分布特征,获得比较满意的分割结果。
2.2 基于区域差异确定优先穿越区域
对重叠区影像进行自适应标记分水岭分割后,需要衡量分割所得区域的差异。本文提出了一种区域差异衡量方法。首先,本文采用文献[12]中的归一化相关系数计算每个像素的差异,即在每个像素的5×5的邻域范围内计算,具体计算方法如式(1)和式(2)
式(1)和式(2)中,f(i,j)与g(i,j)分别为左右影像的像素值,对于多波段影像,取此像素所有波段的平均值作为此像素的值;f-x,y与g-x,y分别为左右影像5×5邻域内的像素平均值。因为NCC(x,y)取值在-1与1之间,需要使用式(3)将其取值转换到0至1之间,即为了提高计算效率,本文使用式(4)计算NCC(x,y)
衡量了像素差异PD(x,y)后,需要进一步衡量区域差异,定义像素差异值超过某阈值TH的点为大差异点,区域差异定义为区域内部大差异点所占区域像素总个数的百分比。基于区域差异确定优先穿越区域的目的是选择低差异的区域作为接缝线优先穿越区域。
接缝线优先穿越区域必须是由连通起止点的区域组成,这里的连通是指通过相邻关系查找可以从起点区域找到终点区域。而这样的区域组合不止一个,为了使选择的区域是差异尽可能小的区域,本文采取文献[12]中最小化最大的思想进行区域选择,即认为所有区域组合中差异最大值最小的组合是最优的区域组合,为了提高算法的效率,本文使用二分查找的策略,并且使用连通算法替换Dijkstra算法确定起止点是否连通,其具体流程如下。
(1) 确定起止区域:包含起始点的区域为起始区域,包含终止点的区域为终止区域。其中,左右影像边界的交点定义为起始点和终止点[12]。
(2) 首先将起始区域和终止区域去掉,然后对剩余区域差异从小到大排序,得数组SortRCR。令L等于0,R等于N-3,N为分割所得区域的个数。
(3) 令tRate=SortRCR[(L+R)/2],将区域差异不大于tRate的区域作为允许通过区域,其他区域作为禁止通过区域,根据区域拓扑关系判断起止点所在区域是否连通。
(4) 若步骤(3)中判断起止点所在区域连通,则令R=(L+R)/2,若不连通,则令L=(L+R)/2。
(5) 若R-L>1,则重复执行步骤(3)和步骤(4),直到R-L≤1,则停止循环,最小最大差异值MinMaxRate寻找完毕,即MinMaxRate=SortRCR[R]。区域差异不大于MinMaxRate的区域与起止区域共同组成了优先穿越区域。
如图 2所示,其中白色的圆点为起始点,黑色的圆点为终止点。图 2(a)为分割得到的区域示意图,其中颜色越深,其区域差异越大。图 2(b)为得到的优先穿越区域,其中白色的区域为优先穿越区域,黑色的区域为禁止穿越区域。
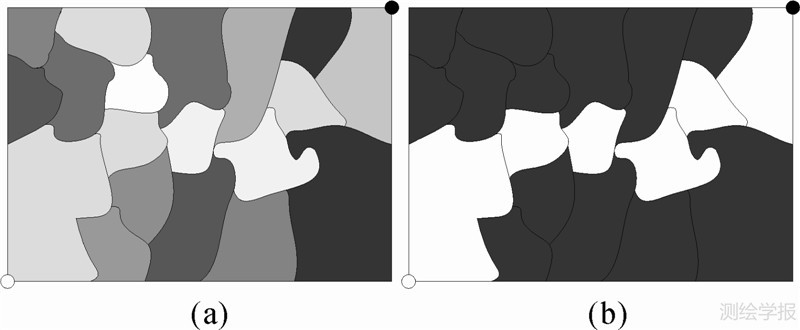 |
| 图 2 优先穿越区示意图 Fig. 2 The demonstration of preferred region |
由于左右重叠区影像存在差异,其分割结果不会相同,左右影像重叠区得到的优先穿越区域也会不同,设左右影像重叠区得到的优先穿越区域分别为PRegion1与PRegion2,最终的优先穿越区域PRegion为左右重叠区优先穿越区域的交集,即:PRegion=PRegion1∩PRegion2。
2.3 优先穿越区中接缝线优化
确定最终优先穿越区域(FPA)后,需要在FPA中对接缝线进行最终的优化,具体步骤如下。
(1) 对像素差异值(PD)进行调整,如式(5)所示
根据最终优先穿越区域对之前求出的像素差异值(PD)进行调整,即将FPA外像素的差异值设置为无穷大,而FPA内像素的差异值则保持不变。
(2) 定义相邻像素间的代价。与文献[21]相似,本文在使用Dijkstra最短路径算法时,为了使接缝线尽量不穿越代价大的点及区域,使用相邻像素差异值的绝对值作为相邻像素之间的代价,如式(6)所示
式中,(u,v)和(k,l)是相邻像素;D(u,v)和D(k,l)是像素点(u,v)和(k,l)处的差异值,计算方法如式(5)所示。(3) 定义Dijkstra最短路径算法最优判据。最短路径算法最优判据如式(7)所示
式中,NBR(u,v)为像素(u,v)相邻像素所组成的点集;Cost(u,v)和Cost(k,l)分别为起始点到像素(u,v)和(k,l)的全局最小差异之和。(4) 使用最小二叉堆对Dijkstra最短路径算法效率进行改进。Dijkstra最短路径算法解决的是非负权值图上单源最短路径问题,其复杂度较大。对于一个有V个顶点和E条边的非负权值图,Dijkstra最短路径算法的时间复杂度为Θ(|V|*|V|+|E|),其算法的总运行时间依赖于最小优先队列的实现,虽然使用斐波拉切堆实现最小优先队列能将其时间复杂度改善到Θ(|V|lg|V|+|E|),但是由于斐波拉切堆的常数因子和编程复杂性使其并不适用于实际应用[27]。考虑到所要解决接缝线优化问题是一个稀疏图的问题,其图的边数为8V,所以本文使用最小二叉堆实现最小优先队列,其时间复杂度为Θ((|V|+|E|)lg|V|)[27],由于E等于8V,即算法复杂度为Θ(9V|lg|V|),很大程度上提高了算法的效率。
3 试验结果与分析
本文所涉及算法均使用C++实现,其中影像读写的代码采用开源的GDAL(geospatial data abstraction library)库。试验中,使用C++编写了相应算法。试验环境为:Inter(R)Core i3,CPU 3.07GHZ,6.00GB内存,Windows 7.0。为了对本文算法进行验证,本文选择两组不同分辨率的高分辨率航空影像进行接缝线的优化试验。数据1为一组大城市中心城区的影像,重叠区影像大小为3030像素×2067像素,分辨率为0.5m;数据2为一组城市郊区的影像,重叠区影像大小为2687像素×4602像素,分辨率为0.2m。本文算法是在待拼接影像已经作了匀光处理的基础上对接缝线进行优化,如果左右影像辐射差异较大,会影响分割结果,进而影响接缝线优化的结果。对于这种情况,建议先作匀光处理,消除左右影像的辐射差异。自适应标记分水岭分割的效果与3个分割参数相关,文献[25, 26]中建议α一般取值0.3~0.5,T一般取值0.6~0.8,A取值为遥感影像上感兴趣地物的最小面积。试验中自适应标记分水岭分割中3个参数设置如下:α=0.4,T=0.65,A=15,大差异点的阈值TH=0.45。为了对比本文算法的效果,选择Dijkstra算法和Chon算法[12]与本文算法进行了比较。
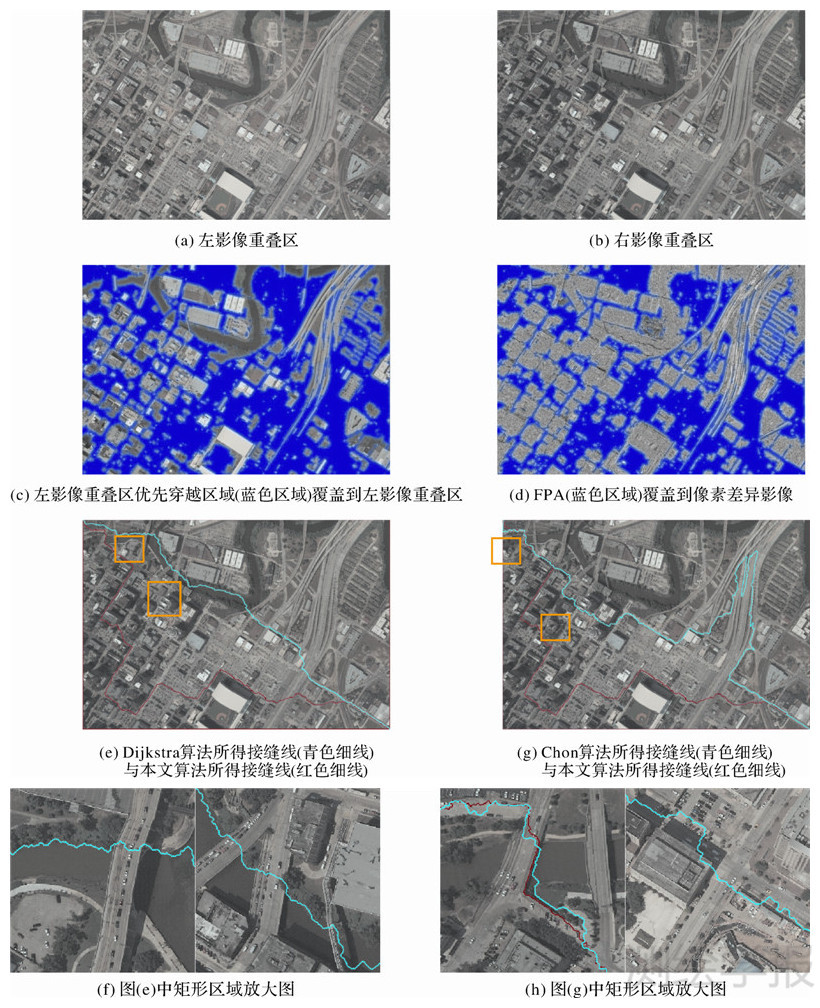
图 3与图 4分别展示了本文算法、Dijkstra算法及Chon算法在数据1与数据2上得到的接缝线及其对比图。图 3与图 4中图(a)和图(b)分别是左右影像重叠区图像。图(c)是左影像重叠区优先穿越区域(蓝色区域)覆盖到左影像重叠区上的效果图。图(d)是FPA(蓝色区域)覆盖到像素差异影像上的效果图。图(e)是Dijkstra算法所得接缝线与本文算法所得接缝线对比图,其中Dijkstra算法所得接缝线为青色细线表示,本文方法所得接缝线为红色细线表示。图(f)是图(e)中矩形区域放大图。图(g)是Chon算法所得接缝线与本文算法所得接缝线对比图,其中Chon算法所得接缝线为青色细线表示,本文方法所得接缝线为红色细线表示。图(h)是图(g)中矩形区域放大图。为了从直观上展示本文方法所得接缝线的拼接效果,图 5中(a)和(b)分别展示了在本文方法所得接缝线基础上的拼接效果图。
 |
| 图 3 数据1接缝线优化试验示意图 Fig. 3 Experiments of seamline optimization of data set one |
 |
| 图 4 数据2接缝线优化试验示意图 Fig. 4 Experiments of seamline optimization of data set two |
为了进一步从定量的角度对本文算法的效果与效率进行评价,本文采取接缝线上的像元个数、穿越高差明显地物个数以及处理时间3个指标对算法进行评价,并与Dijkstra算法和Chon算法进行了比较,比较结果如表 1所示。
图 3是本文算法、Dijkstra算法及Chon算法在数据1上所得接缝线的对比图。数据1分辨率为0.5m,是大城市中心城区的影像,重叠区域影像中高楼及桥梁(包括立交桥)比较多,这也是差异较大的地物类型,理想的接缝线就是要避免穿越这些地物类型。图 3(e)、图 3(f)、图 3(g)及图 3(h)表明,Dijkstra算法与Chon算法所得接缝线都穿越了差异较大的地物,其中Dijkstra算法穿越了5座桥梁,Chon算法穿越了1座桥梁和2座房屋;如图 3(c)、图 3(d)所示,由于本文算法在选择优先穿越区域时,已经将大部分差异较大的地物(如高楼、大型桥梁等)排除,然后在优先穿越区域中优化接缝线,其得到的接缝线没有穿越差异较大的地物,主要是在道路、广场及水域中行进,保证了拼接影像的质量。
图 4是本文算法、Dijkstra算法及Chon算法在数据2上所得接缝线的对比图。数据2分辨率为0.2m,是城市郊区的影像,重叠区域中包括农田、厂房、居民区、道路及裸地等地物类型。图 4(e)、图 4(f)、图 4(g)及图 4(h)表明,Dijkstra算法与Chon算法所得接缝线都穿越了差异较大的地物,其中Dijkstra算法穿越了1座大的房屋,Chon算法穿越了1座房屋和1堵围墙;如图 4(c)、图 4(d)所示,由于本文算法在选择优先穿越区域时,已经将大部分差异较大的地物(如厂房、居民楼等)排除,再在优先穿越区域中优化接缝线,其得到的接缝线没有穿越差异较大的地物,主要是在道路、平地及裸地中行进,保证了拼接影像的质量。
图 5展示了数据1和数据2基于本文方法获得接缝线拼接后的图像,拼接时采取接缝线左边重叠区像元取值左影像对应像元像素值,拼接线右边重叠区像元取值右影像对应像元像素值。为了更好地反映接缝线的质量,没有对接缝线附近像元做羽化处理。图 5表明,本文方法将大部分差异较大的地物排除在接缝线优先穿越区域外,其得到的接缝线主要沿着道路、广场、平地等差异较小的区域中行进,能得到质量较好的拼接影像。
 |
| 图 5 两组数据拼接示意图 Fig. 5 The mosaicked image of two data sets |
表 1表明,对于Dijkstra算法,其接缝线上的像素个数最少,即接缝线最短,但是其穿越的高差明显的地物个数也是最多,在数据1中穿越了5座桥梁,数据2中穿越了1座房屋;对于Chon算法,其接缝线上的像素个数最多,即接缝线最长,也穿越了高差明显的地物,在数据1中穿越了1座桥梁和2座房屋,数据2中穿越了1座房屋和1堵围墙;对于本文算法,其接缝线上的像素个数居于前两种方法之间,但是避开了穿越高差明显的地物,在两组试验中,本文方法均没有穿越高差明显的地物。对于处理效率而言,本文算法具有最高的效率,Dijkstra算法其次,Chon算法效率最低,Dijkstra算法处理时间是本文算法的61.34倍,Chon算法处理时间是本文算法的1850.53倍。
| 数据 | 方法 | 接缝线上 像素个数 | 穿越高差明显 地物个数 | 处理时 间/s |
| 数据1 | Dijkstra | 3992 | 5座桥梁 | 344.269 |
| Chon | 7388 | 1座桥梁和 2座房屋 | 14647.945 | |
| 本文方法 | 6282 | 无 | 14.227 | |
| 数据2 | Dijkstra | 6650 | 1座房屋 | 1296.745 |
| Chon | 11232 | 1座房屋和 1堵围墙 | 86015.554 | |
| 本文方法 | 7334 | 无 | 40.170 |
本文基于自适应分水岭分割算法提出了一种航空影像接缝线优化方法,该方法将图像分割引入接缝线优化中,使用自适应分水岭算法得到分割区域,然后统计区域差异,使用最小化最大差异思想确定接缝线优先穿越区域,从而将建筑物等差异较大的地物排除在优先穿越区域中,最后在优先穿越区域中得到最终的接缝线。与Dijkstra算法及Chon算法对比试验表明,本文方法在效果和效率上都优于这两种算法。
由于自适应分水岭算法的效果对本文算法所得的接缝线有一定的影响,即分割参数的设置对最终得到的接缝线有一定的影响,下一步需要研究如何根据影像内容自适应地确定分割参数,满足接缝线优化的应用需求。
| [1] | ZUO Zhiquan, ZHANG Zuxun, ZHANG Jianqing, et al. Seamlines Intelligent Detection in Large-scale Urban Orthoimage Mosaicking[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 84-89. (左志权, 张祖勋, 张剑清, 等. DSM辅助下城区大比例尺正射影像镶嵌线智能检测[J]. 测绘学报, 2011, 40(1): 84-89.) |
| [2] | ZHOU Qinghua, PAN Jun, LI Deren. Overview of Automatic Generation of Mosaicking Seamlines for Remote Sensing Images[J]. Remote Sensing for Land and Resources, 2013, 25(2): 1-7. (周清华, 潘俊, 李德仁. 遥感图像镶嵌接缝线自动生成方法综述[J]. 国土资源遥感, 2013, 25(2): 1-7.) |
| [3] | PAN Jun. Research on Automatic Color Consistency Processing and Generation of Seamline Network for Aerial Images[D]. Wuhan: Wuhan University, 2008. (潘俊. 正射影像全自动快速制作关键技术研究[D]. 武汉: 武汉大学, 2008.) |
| [4] | MILGRAM D L. Computer Methods for Creating Photomosaics[J]. IEEE Transactions on Computers, 1975, C-24(11): 1113-1119. |
| [5] | FERNANDEZ E, GARFINKEL R, ARBIOL R. Mosaicking of Aerial Photographic Maps via Seams Defined by Bottleneck Shortest Paths[J]. Operations Research, 1998, 46(3): 293-304. |
| [6] | FERNáNDEZ E, MARTí R. GRASP for Seam Drawing in Mosaicking of Aerial Photographic Maps[J]. Journal of Heuristics, 1999, 5(2): 181-197. |
| [7] | AFEK Y, BRAND A. Mosaicking of Orthorectified Aerial Images[J]. Photogrammetric Engineering & Remote Sensing, 1998, 64(2): 115-125. |
| [8] | KERSCHNER M. Seamline Detection in Colour Orthoimage Mosaicking by Use of Twin Snakes[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2001, 56(1): 53-64. |
| [9] | ZHANG Jiangqing, SUN Mingwei, ZHANG Zuxun. Automated Seamline Detection for Orthophoto Mosaicking Based on Ant Colony Algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 675-678. (张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 675-678.) |
| [10] | SUN Mingwei. Research on Key Technology of Automatic and Fast DOM Generation[D]. Wuhan: Wuhan University, 2009. (孙明伟. 正射影像全自动快速制作关键技术研究[D]. 武汉: 武汉大学, 2009.) |
| [11] | SOILLE P. Morphological Image Compositing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2006, 28(5): 673-683. |
| [12] | CHON J, KIM H, LIN C S. Seam-line Determination for Image Mosaicking: A Technique Minimizing the Maximum Local Mismatch and the Global Cost[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2010, 65(1): 86-92. |
| [13] | YUAN Xiuxiao, ZHONG Can. An Improvement of Minimizing Local Maximum Algorithm on Searching Seam Line for Orthoimage Mosaicking[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 199-204. (袁修孝, 钟灿. 一种改进的正射影像镶嵌线最小化最大搜索算法[J]. 测绘学报, 2012, 41(2): 199-204.) |
| [14] | MAH C, SUNJ. Intelligent Optimization of Seam-line Finding for Orthophoto Mosaicking with LiDAR Point Clouds[J]. Journal of Zhejiang University Science C, 2011, 12(5): 417-429. |
| [15] | SUN Jie. Research on Optimization of Ortho-image Mosaic Seamline in Airborne LiDAR System[J]. Computer Engineering and Applications, 2010, 46(18): 15-17. (孙杰. 机载LIDAR系统正射影像镶嵌线优化算法研究[J]. 计算机工程与应用, 2010, 46(18): 15-17.) |
| [16] | SUN Jie, MA Hongchao, TANG Xuan. Optimization of LiDAR System Ortho-image Mosaic Seam-line[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 325-328. (孙杰, 马洪超, 汤璇. 机载LiDAR正射影像镶嵌线智能优化研究[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 325-328.) |
| [17] | SUN Jie. Research on Key Issue of Airborne LiDAR Based True-orthophoto Production[D]. Wuhan: Wuhan University, 2011. (孙杰. 机载LiDAR点云数据辅助真正射影像制作关键技术研究[D]. 武汉: 武汉大学, 2011.) |
| [18] | WANG D L, WAN Y C, XIAO J H, et al. Aerial Image Mosaicking with the Aid of Vector Roads[J]. Photogrammetric Engineering & Remote Sensing, 2012, 78(11): 1141-1150. |
| [19] | WAN Y C, WANG D L, XIAO J H, et al. Tracking of Vector Roads for the Determination of Seams in Aerial Image Mosaics[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 328-332. |
| [20] | WAN Y C, WANG D L, XIAO J H, et al. Automatic Determination of Seamlines for Aerial Image Mosaicking Based on Vector Roads Alone[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2013, 76: 1-10. |
| [21] | PAN J, ZHOU Q H, WANG M. Seamline Determination Based on Segmentation for Urban Image Mosaicking[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(8): 1335-1339. |
| [22] | GONZALEZ R C, WOODS R E. Digital Image Processing[M]. 2nd ed. Upper Saddle River, NJ:Prentice Hall, 2002. |
| [23] | MEYER F, BEUCHER S. Morphological Segmentation[J]. Journal of Visual Communication and Image Representation, 1990, 1(1): 21-46. |
| [24] | VINCENT L, SOILLEP. Watersheds in Digital Spaces: An Efficient Algorithm Based on Immersion Simulations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1991, 13(6): 583-598. |
| [25] | WU Zhaocong, HU Zhongwen, OUYANG Qundong. A Regional Adaptive Segmentation Algorithm for Remote Sensing Image[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 293-296. (巫兆聪, 胡忠文, 欧阳群东. 一种区域自适应的遥感影像分水岭分割算法[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 293-296.) |
| [26] | LI D R, ZHANG G F, WU Z C, et al. An Edge Embedded Marker-based Watershed Algorithm for High Spatial Resolution Remote Sensing Image Segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(10): 2781-2787. |
| [27] | CORMENT H, LEISERSON C E, RIVEST R L, et al. Introduction to Algorithms[M]. 2nd ed. Cambridge: MIT Press,2001." |