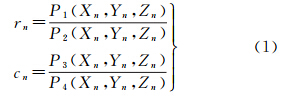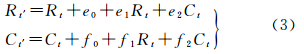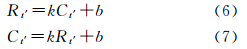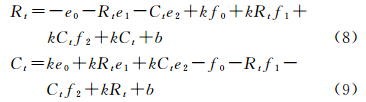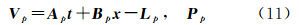2. 武汉大学地球空间信息技术协同创新中心,湖北 武汉 430079;
3. 武汉大学遥感信息工程学院,湖北 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
1 引 言
高分辨率卫星影像区域网平差是实现卫星影像精确几何定位的一种常用方法。目前,高分辨率卫星影像区域网平差以地面控制点作为控制条件,在求解卫星影像精确定向参数的同时,获得连接点的地面三维坐标。然而,随着地形图修测与更新、目标变化检测需求的不断增加,如何以地形图中大量存在的线特征作为控制条件,进行高分辨率卫星影像区域网平差,以实现卫星影像与地形图的精确配准,显得愈发重要。此外,随着国家基础地理信息库的不断完善,我国已经积累了大量的地形图数据,充分利用这些地形图中的线特征信息,可以有效减少甚至避免野外控制点的测量,具有非常重要的应用价值。
相比于点特征,利用线特征进行摄影测量数据处理时,物方直线在影像上对应的像方直线不要求完全可见,即物方和像方所对应直线的端点不要求是同名点[1]。近年来,针对线特征在摄影测量数据处理中的应用,已经开展了一系列的研究:文献[1]利用控制直线分别进行航空、卫星影像自动绝对定向,取得了像素级的定向精度[1];文献[2]研究了基于线特征的遥感影像与矢量图的匹配方法;文献[3]以直线特征作为配准基元,研究了多源卫星影像的自动配准方法;文献[4,5,6]同时利用点、线特征进行航空影像相对定向和空间后方交会;文献[7]研究了利用矢量地形图中直线特征进行航空影像几何定位的方法;文献[8]研究了直线特征约束的航空相机自检校光束法区域网平差方法;文献[9]研究了直线特征约束的高分辨率卫星影像绝对定向方法;文献[10,11]研究了点、线特征约束的高分辨率卫星影像区域网联合平差方法,并通过CBERS-2B影像验证了方法的可行性;文献[12]研究了直线特征约束的SPOT影像几何纠正方法,解决了控制点选取困难地区的SPOT影像几何纠正问题。
现有的直线特征约束的航空/卫星影像几何定位通常从传感器的成像机理出发,以共面条件作为几何约束,建立严格的几何模型,并实施影像几何定位。然而,对于高分辨率卫星影像而言,很多影像供应商(如GeoEye-1、IKONOS)只提供各景影像的有理多项式系数(rational polynomial coefficients,RPC),用于构建有理函数模型(rational function model,RFM),而不再提供构建影像严格几何模型所必需的传感器参数、姿轨数据等。因此,高分辨率卫星影像用户将难以从影像严格几何模型出发,实施直线特征约束的影像几何定位。鉴于此,本文以RFM作为影像几何处理模型,研究一种适用于影像用户的直线特征约束的区域网平差方法,以充分利用现有地形图中的直线特征作为控制条件,实现高分辨率卫星影像的精确几何定位。
2 区域网平差模型的建立
在进行直线特征约束的高分辨率卫星影像区域网平差时,控制直线为区域网平差提供地面控制条件,影像连接点为区域网平差提供影像之间的内部几何约束。因此,根据区域网平差所采用的几何特征的类型,直线特征约束的高分辨率卫星影像区域网平差模型可以分为两类:一类是基于点特征的区域网平差模型;另一类是基于直线特征的区域网平差模型。
2.1 基于点特征的区域网平差模型
就点特征而言,“RFM+仿射变换模型”通常被用作高分辨率卫星遥感影像区域网平差的数学模型[13, 14]。其中,RFM是一种通用的几何处理模型,具有优良的内插特性,且形式简单。利用RFM拟合高分辨率卫星影像的严格几何模型可以取得很高的拟合精度[15, 16, 17],可以用RFM代替严格几何模型进行影像几何纠正、正射影像制作和目标三维重建等[18, 19, 20]。因此,很多影像供应商已将RPC参数作为元数据的一部分提供给用户,以达到隐藏传感器核心参数的目的。
RFM的表达形式为[13]
式中,(Xn,Yn,Zn)和(rn,cn)分别为地面点坐标(X,Y,Z)和像点坐标(R,C)经平移和缩放后的正则化坐标;Pi(Xn,Yn,Zn)(i=1,2,3,4)是以X、Y和Z为自变量的三阶多项式。
以RFM作为影像几何处理模型,高分辨率卫星影像的区域网平差模型为
式中,(Ro,Co)和(Rs,Cs)分别为像点坐标的正则化平移参数和缩放系数;(e0,e1,e2,f0,f1,f2)为仿射变形参数,(e0+e1R+e2C,f0+f1R+f2C)即为像点坐标(R,C)的系统误差改正值。
2.2 基于直线特征的区域网平差模型
如图 1所示,线L为物方空间由已知控制点P1、P2确定的一条控制直线;线lP为像方空间由点p1、p2确定的直线(称之为“预测直线”),其中,点p1、p2分别为根据式(1)将地面点P1、P2投影至像方得到的投影点;线lT为物方直线L在像方空间的对应直线(称之为“观测直线”),点t为直线lT上的任意一个像点。
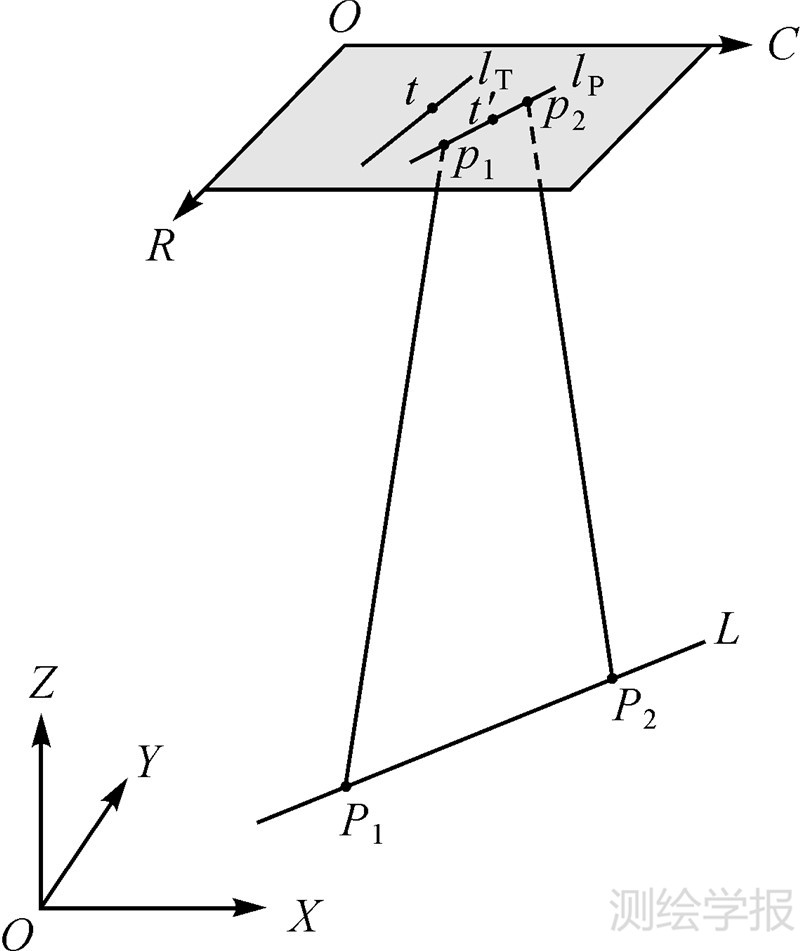 |
| 图 1 控制直线成像示意图 Fig. 1 Imaging sketch map of CSLs |
若RPC参数不包含误差,则观测直线lT与预测直线lP必然重合。依据这一原理,便可建立基于直线特征的高分辨率卫星影像区域网平差模型。
利用RFM拟合高分辨率卫星影像严格几何模型的拟合误差可以忽略不计,但由于受到卫星位置与姿态观测等误差的影响,直接利用由地形无关方案求解获得的RPC参数进行卫星影像几何定位,其定位结果仍包含明显的系统误差[13],即RPC参数包含系统误差。就图 1而言,RPC参数中的系统误差会导致直线lT偏离直线lP。因此,为了满足“观测直线lT与预测直线lP必然重合,即观测直线lT上的任意像点t位于直线lP上”这个几何约束条件,需要对直线lT上的像点t进行系统误差改正。
设点t′为像点t经系统误差改正得到的像点,则像点t′应位于直线lP上,而且像点t与t′的像平面坐标满足
式中,(Rt,Ct)、(Rt′,Ct′)分别为像点t与t′的像平面坐标。
对于像平面内的直线lP,可以采用点斜式、两点式、斜截式等数学表达式表示。为了便于推导基于直线特征的高分辨率卫星影像区域网平差模型,本文采用斜截式表示直线lP。同时,为了顾及直线斜率过大对区域网平差精度的影响,本文根据直线lP与像平面坐标系O-RC的C轴之间夹角的大小,将其分为两种情况分别进行处理:当直线lP与C轴之间的夹角θ满足-45°≤θ≤45°或者135°≤θ≤225°时,直线lP的表达式如式(4)所示
当45°<θ<135°和225°<θ<315°时,直线lP的表达式如式(5)所示 式(4)和式(5)中,k和b分别为直线lP的斜率和截距,可由像点p1、p2的像平面坐标计算获得。
由于像点t′位于直线lP上,因此像点t′应满足式(6)或者式(7),即
将式(3)分别代入式(6)和式(7),并整理可得
式(8)和式(9)即为基于直线特征的高分辨率卫星影像区域网平差模型。 3 区域网平差参数的求解
进行直线特征约束的高分辨率卫星影像区域网平差时,需要根据控制直线和影像连接点分别建立误差方程,并联立两类误差方程,以便求解出各景影像的仿射变形参数和各个影像连接点的地面三维坐标。
由2.2节可以看出,像点t是直线lT上的任意一个像点,而并非地面点P1、P2的对应像点。也就是说,根据控制直线建立观测方程(式(8)或式(9))时,只要求物方直线与像方直线相对应,而无须物方直线上的地面点与像方直线上的像点一一对应。
理论上讲,根据直线lT上的每一个像点坐标观测值都可以建立一个观测方程。但是,就同一条直线而言,增加观测方程的数量并不能有效解决法方程的秩亏问题[21, 22]。因此,本文仅利用同一条直线上的两个像点坐标观测值建立观测方程,区域网平差参数求解的具体过程如下:
(1) 针对每一条控制直线L,根据式(1)将直线L上两个已知控制点P1、P2分别投影至像方,得到投影点p1、p2,并根据投影点的像平面坐标计算直线lP的斜率k和截距b;
(2) 依据式(8)或式(9),利用直线lT上两个像点t1、t2的像平面坐标观测值(Rt1,Ct1)、(Rt2,Ct2)建立误差方程
式中,t=[Δe0Δe1Δe2Δf0Δf1Δf2]T为仿射变形参数的改正数;Pl为像点t1、t2的坐标观测值的权矩阵;对于式(8),Al=
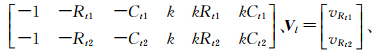 、Ll=
、Ll=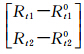 ;对于式(9),Vl=
;对于式(9),Vl=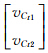 、Al=
、Al=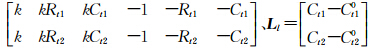 。
。(3) 对于每一个影像连接点p(Rp,Cp),根据式(2)建立误差方程
式中,Vp=
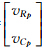 ;x=[ΔXΔYΔZ]T;Lp=
;x=[ΔXΔYΔZ]T;Lp=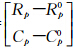 ;Ap=
;Ap=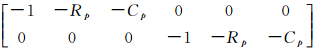 ;
Bp=
;
Bp=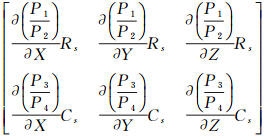 ;Pp为影像连接点坐标观测值的权矩阵。
;Pp为影像连接点坐标观测值的权矩阵。(4) 联立式(10)和式(11),并根据最小二乘平差原理求解未知数t、x,可得
4 试验结果与分析 4.1 试验设计本节分别利用覆盖美国圣迭戈试验区的两景IKONOS影像、美国斯波坎试验区的两景QuickBird影像和法国普罗旺斯试验区的两景SPOT-5影像进行试验验证,各试验区的基本参数如表 1所示。受试验条件的限制,笔者未能获得国内或者国外覆盖同一试验区的高分辨率卫星影像和地形图数据,因而采用Google Earth代替圣迭戈、斯波坎和普罗旺斯试验区的地形图,以验证本文方法的正确性和可行性。试验区内的控制直线与检查点均由人工在Google Earth上量测获得,控制直线均匀分布于影像覆盖区域的周边与中心,如图 2所示。就控制直线而言,先从Google Earth上量测直线特征的两个端点的地面三维坐标,再在卫星影像上量测同名直线的两个像点的像平面坐标。需要说明的是,Google Earth上直线特征的两个端点并不需要与卫星影像上同名直线的两个像点一一对应。
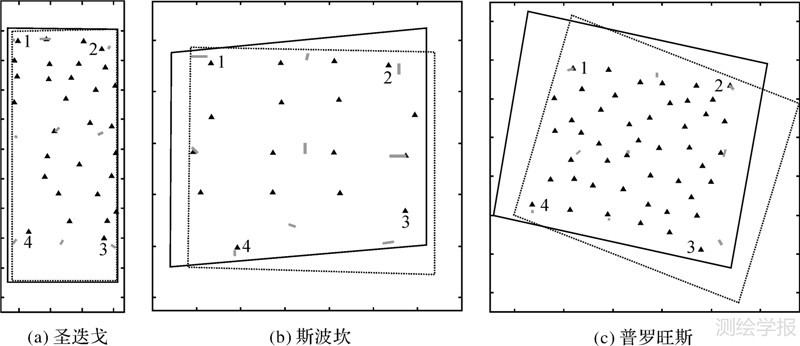 |
| 图 2 各试验区内控制点与控制直线的分布 Fig. 2 Distributions of GCPs and CSLs in each empirical area |
| 试验区 | 影像类型 | 获取时间 | 影像大小/(像素×像素) | 高程范围/m | 控制直线数/条 | 控制点数/个 |
| 圣迭戈 | IKONOS | 2000-02-07 | 19 039×6645 | 3~134 | 9 | 30 |
| 2000-02-07 | 19 038×6193 | |||||
| 斯波坎 | QuickBird | 2002-08-28 | 12 000×12 000 | 577~728 | 9 | 17 |
| 2002-08-28 | 12 000×12 000 | |||||
| 普罗旺斯 | SPOT-5 | 2002-08-15 | 12 000×12 000 | 5~296 | 9 | 47 |
| 2002-08-18 | 12 000×12 000 |
为了分析控制直线的数量与分布对高分辨率卫星影像区域网平差精度的影响,本节设计了5种控制直线布设方案,如图 3所示。根据第3节中的具体流程,在不同的控制直线布设方案下,利用Google Earth上量测的控制直线分别进行高分辨率卫星影像区域网平差,获得各景影像的仿射变形参数和各个检查点的地面三维坐标,并根据检查点在Google Earth上的量测坐标统计获得检查点的最大残差和中误差,列于表 2。
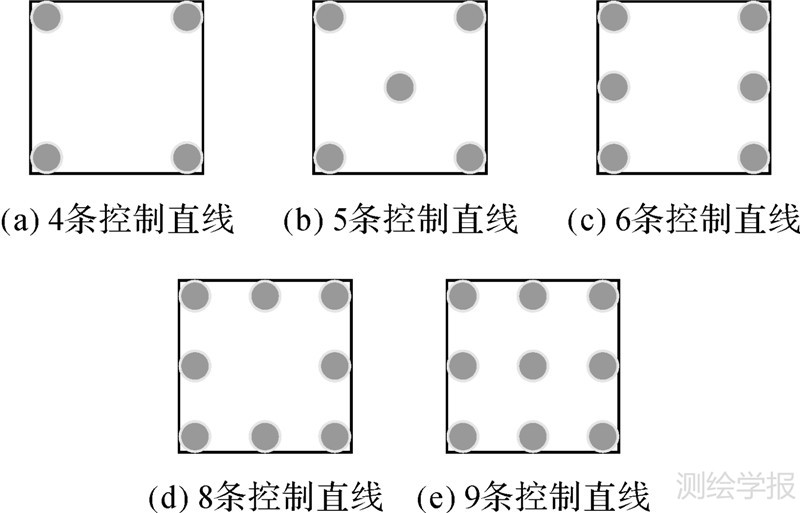 |
| 图 3 控制直线的布设方案 Fig. 3 Layout scenarios of CSLs |
| 试验区 | 控制直线 数量 | 检查 点数 | 最大残差/m | 中误差/m | ||||||
| X | Y | 平面 | Z | X | Y | 平面 | Z | |||
| 圣迭戈 | 4 | 30 | -10.989 | -15.219 | 16.545 | -17.327 | 6.736 | 7.789 | 10.298 | 9.532 |
| 5 | 30 | -3.821 | -2.571 | 4.312 | 3.305 | 1.628 | 1.357 | 2.119 | 1.764 | |
| 6 | 30 | 2.106 | 2.466 | 3.050 | 2.405 | 1.063 | 1.224 | 1.621 | 1.202 | |
| 8 | 30 | -1.236 | -1.334 | 1.348 | 1.445 | 0.562 | 0.649 | 0.859 | 0.683 | |
| 9 | 30 | -1.196 | -1.436 | 1.441 | 1.505 | 0.559 | 0.700 | 0.896 | 0.710 | |
| 斯波坎 | 4 | 17 | 3.836 | -1.828 | 4.029 | -2.641 | 1.912 | 0.925 | 2.124 | 1.233 |
| 5 | 17 | 6.080 | -2.792 | 6.527 | -2.966 | 2.967 | 1.476 | 3.314 | 1.300 | |
| 6 | 17 | -0.576 | 1.237 | 1.285 | -0.677 | 0.399 | 0.645 | 0.758 | 0.327 | |
| 8 | 17 | -0.625 | 1.136 | 1.149 | -0.923 | 0.314 | 0.527 | 0.614 | 0.445 | |
| 9 | 17 | 0.784 | 1.120 | 1.124 | -0.784 | 0.374 | 0.502 | 0.627 | 0.386 | |
| 普罗旺斯 | 4 | 47 | 147.041 | 158.273 | 216.036 | -170.319 | 81.468 | 73.916 | 110.003 | 90.166 |
| 5 | 47 | 183.513 | 201.086 | 272.236 | -213.306 | 100.488 | 96.292 | 139.176 | 113.173 | |
| 6 | 47 | 9.042 | -13.007 | 13.601 | 8.202 | 4.791 | 6.125 | 7.776 | 3.679 | |
| 8 | 47 | 6.743 | -7.960 | 8.370 | -8.396 | 3.136 | 3.946 | 5.041 | 3.380 | |
| 9 | 47 | 6.234 | -6.612 | 7.993 | -8.813 | 2.941 | 3.841 | 4.838 | 3.409 | |
分析表 2中的试验结果可以看出:
(1) 在有4条控制直线的情况下,各试验区影像区域网平差并没有达到预期的精度。以覆盖圣迭戈试验区的IKONOS影像为例,区域网平差获得的平面与高程精度仅分别达到10.298m、9.532m。理论上讲,以3条控制直线作为地面控制条件,即可精确求解出各景影像的仿射变形参数(e0,e1,e2,f0,f1,f2)。但是,在控制直线较少的情况下,求解出的(e0,e1,e2,f0,f1,f2)与其真值之间容易出现较大的偏差。究其原因就在于,在建立基于直线特征的卫星影像区域网平差模型时,仅要求图 1中的观测直线lT与预测直线lP必须重合,而无法约束这两条直线上的对应像点必须重合。在此前提下,利用较少的控制直线进行影像区域网平差时,直线lT与直线lP之间容易沿直线方向产生偏移,从而引起整体性的仿射变形,使得求解出的(e0,e1,e2,f0,f1,f2)偏离其真值。同样以圣迭戈试验区为例,令直线lT经系统误差改正后的直线为l′T,直线l′T与直线lP之间的重合误差(即式(10)中的Ll)如图 4所示,偏移量如图 5所示。从图 4、图 5中可以看出,利用4条控制直线进行影像区域网平差时,虽然直线l′T与直线lP之间的重合误差优于0.5像素,但由于缺少对应像点的重合约束,直线l′T与直线lP之间仍产生了偏移,最大偏移量高达约25像素。因此,求解出的(e0,e1,e2,f0,f1,f2)仍存在较大的误差,从而导致圣迭戈试验区影像的区域网平差结果仍含有明显的系统误差,如图 6(a)所示。
 |
| 图 4 直线重合误差 Fig. 4 Coinciding errors between straight lines |
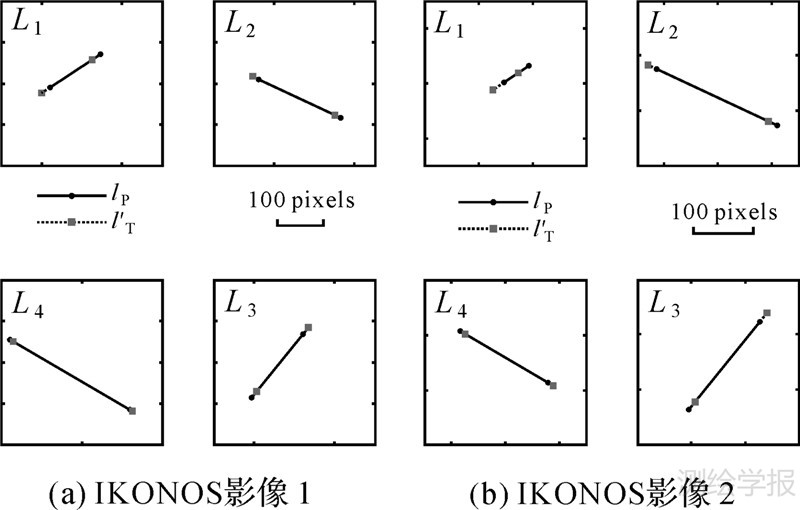 |
| 图 5 直线偏移量 Fig. 5 Offsets between straight lines |
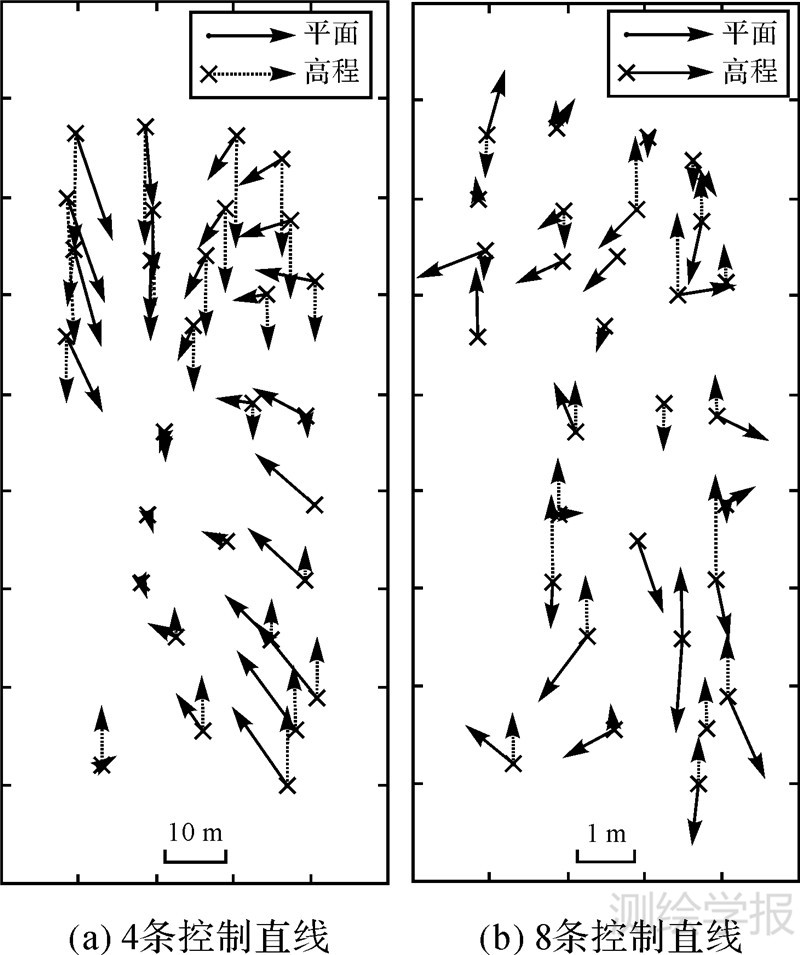 |
| 图 6 圣迭戈试验区检查点残差分布图 Fig. 6 Residual error distribution of the check points in San Diego area |
(2) 当控制直线的数量增加至5条或者6条时,亦不能很好地解决直线l′T与直线lP之间的偏移问题,各试验区影像的区域网平差结果仍存在较大的误差。同样以圣迭戈试验区为例,区域网平差获得的平面和高程精度分别为1.621m和1.202m,而相比于利用9条控制直线获得的区域网平差精度,仍分别存在0.725m和0.492m的偏差。
(3) 随着控制直线数量的进一步增加,影像区域网平差精度也在逐步改善。当控制直线的数量增加至8条,即沿影像覆盖区域的周边布设8条控制直线时,各试验区影像的区域网平差精度趋于稳定。也就是说,增加控制直线的数量可以在保证直线l′T与直线lP之间重合度的同时,改善两者之间的偏移情况,从而减小各景影像仿射变形参数与其真值之间的偏差,提高高分辨率卫星影像的区域网平差精度。就圣迭戈试验区而言,区域网平差获得的平面和高程精度均优于1个像素,而且区域网平差结果不再包含系统误差,如图 4(b)所示。而对于斯波坎试验区和普罗旺斯试验区,亦取得了优于1个像素的区域网平差精度。
综上可以看出,本文提出的直线特征约束的高分辨率卫星影像区域网平差方法是正确可行的,而为了有效解决观测直线与预测直线之间的偏移问题,获得最佳的高分辨率卫星影像区域网平差精度,需要在影像覆盖区域的周边布设8条及以上控制直线。
4.3 控制直线长度对区域网平差精度的影响
本节在4.2节各试验区中8条控制直线的基础上,分别利用5组不同长度的控制直线进行高分辨率卫星影像区域网平差,以便分析控制直线长度对区域网平差精度的影响。受文章篇幅的限制,本节只列出了圣迭戈试验区的区域网平差结果,如表 3所示。
从表 3中的试验结果可以看出,控制直线长度对影像区域网平差精度的影响很小。当控制直线的长度由[20, 30]像素增加至[140, 150]像素时,区域网平差后的平面和高程精度差异仅分别为0.030m和0.037m,这也为本文方法的顺利实施提供了便利条件。
| 控制直线 数量 | 控制直线长度 /像素 | 检查 点数 | 最大残差/m | 中误差/m | ||||||
| X | Y | 平面 | Z | X | Y | 平面 | Z | |||
| 8 | [20,30] | 30 | -1.437 | -1.124 | 1.666 | -1.037 | 0.663 | 0.598 | 0.893 | 0.570 |
| 8 | [50,60] | 30 | -1.268 | -1.179 | 1.569 | 1.433 | 0.598 | 0.590 | 0.839 | 0.645 |
| 8 | [80,90] | 30 | -1.337 | -1.140 | 1.480 | 1.266 | 0.628 | 0.581 | 0.855 | 0.595 |
| 8 | [110,120] | 30 | -1.220 | -1.296 | 1.484 | 1.361 | 0.577 | 0.619 | 0.846 | 0.677 |
| 8 | [140,150] | 30 | -1.301 | -1.253 | 1.319 | 1.275 | 0.562 | 0.655 | 0.863 | 0.607 |
为了便于比较分析,本节在各个试验区的4角分别选取了一个地面控制点,并进行基于控制点的高分辨率卫星影像区域网平差。地面控制点的分布如图 2中1—4号点所示,影像区域网平差结果列于表 4。
| 试验区 | 控制 点数 | 检查 点数 | 最大残差/m | 中误差/m | ||||||
| X | Y | 平面 | Z | X | Y | 平面 | Z | |||
| 圣迭戈 | 4 | 26 | -1.237 | -1.308 | 1.800 | 1.477 | 0.593 | 0.634 | 0.868 | 0.708 |
| 斯波坎 | 4 | 13 | 0.749 | -0.880 | 0.941 | 0.754 | 0.419 | 0.515 | 0.664 | 0.446 |
| 普罗旺斯 | 4 | 43 | -7.058 | 10.065 | 10.066 | 8.970 | 3.154 | 4.556 | 5.541 | 3.584 |
对比表 2和表 4中的试验结果可以看出,以控制直线作为地面控制条件和以控制点作为地面控制条件所获得的影像区域网平差精度基本一致。就数量而言,4个地面控制点即可满足影像区域网平差的需求,而为了消除观测直线与预测直线之间偏移的影响,需要8条控制直线才能够精确求解出各景影像的仿射变形参数,从而实现高分辨率卫星影像的精确几何定位。但是在卫星影像所覆盖的地面范围内,从现有地形图上获取沿影像覆盖区域周边分布的8条控制直线并非难事,特别是在城市地区。另外,相比于点特征,从现有地形图上获取直线特征具有更高的可操作性和可靠性,这也为直线特征约束的高分辨率卫星影像区域网平差提供了可行性。
5 结束语
本文以“像方观测直线与像方预测直线必须重合”作为几何约束条件,提出了一种直线特征约束的高分辨率卫星影像区域网平差方法,该方法可以用于解决地形图修测与更新、目标变化检测时的影像几何定位问题。同基于控制点的卫星影像区域网平差方法相比,本文方法的最大优势在于:在建立基于直线特征的影像区域网平差模型时,只需要物方直线与像方直线相对应,而无须直线上的点一一对应。试验结果表明,本文方法可以充分利用现有地形图中的线特征作为控制条件,在沿影像覆盖区域周边布设8条控制直线的情况下,可以获得与基于控制点的影像区域网平差相一致的精度。此外,本文方法也可以同时利用现有的控制点与控制直线条件,联合求解卫星影像的仿射变形参数和连接点的地面三维坐标,实现卫星影像的精确几何定位。由于受试验数据的限制,文中的控制直线与检查点的地面三维坐标均从Google Earth上量测获得,本文方法的正确性与可行性仍需要利用大量真实的地形图数据进行进一步的验证,而且控制直线的方向对本文方法的影响亦有待于进一步研究。
| [1] | ZHANG Zuxun, ZHANG Hongwei, ZHANG Jianqing. Automatic Absolute Orientation of Remote Sense Image by Line Photogrammetry[J]. Journal of Image and Graphics, 2005, 10(2): 213-217. (张祖勋, 张宏伟, 张剑清. 基于直线特征的遥感影像自动绝对定向[J]. 中国图象图形学报, 2005, 10(2): 213-217.) |
| [2] | LIN Yi, ZHANG Shaoming, CHEN Yingying. Line Feature-based Matching between Imagery and Vector Map[J]. Journal of Tongji University: Natural Science, 2010, 38(4): 598-603. (林怡, 张绍明, 陈映鹰. 基于线特征的影像与矢量的匹配[J]. 同济大学学报: 自然科学版, 2010, 38(4): 598-603.) |
| [3] | HABIB A F, ALRUZOUQ R I. Line-based Modified Iterated Hough Transform for Automatic Registration of Multi-source Imagery[J]. The Photogrammetric Record, 2004, 19(105): 5-21. |
| [4] | ZHANG Yongjun, HU Binghua, ZHANG Jianqing. Relative Orientation Based on Multiple Conjugate Features[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 194-199. (张永军, 胡丙华, 张剑清. 基于多种同名特征的相对定向方法研究[J]. 测绘学报, 2011, 40(2): 194-199.) |
| [5] | FU Zhongliang, ZHOU Fan, YU Zhiqiang. A Space Resection Synthesized the Multiple Features[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 827-834. (付仲良, 周凡, 俞志强. 综合多种特征的后方交会法[J]. 测绘学报, 2014, 43(8): 827-834.) |
| [6] | HABIB A F, LIN H T, MORGAN M. Autonomous Space Resection Using Point-and Line-based Representation of Free-form Control Linear Features[J]. The Photogrammetric Record, 2003, 18(103): 244-258. |
| [7] | KARJALAIN M, HYYPPÄ J, KUITTINEN R. Determination of Exterior Orientation Using Linear Features from Vector Maps[J]. The Photogrammetric Record, 2006, 21(116): 329-341. |
| [8] | HABIB A F, MORGAN M, LEE Y R. Bundle Adjustment with Self-Calibration Using Straight Lines[J]. The Photogrammetric Record, 2002, 17(100): 635-650. |
| [9] | TOMMASELLI A M G, MEDEIROS N G. Determination of the Indirect Orientation of Orbital Pushbroom Images Using Control Straight Lines[J]. The Photogrammetric Record, 2010, 25(130): 159-179. |
| [10] | JUNIOR J M, TOMMASELLI A M G. Exterior Orientation of CBERS-2B Imagery Using Multi-Feature Control and Orbital Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 79: 219-225. |
| [11] | TOMMASELLI A M G,JUNIOR J M. Bundle Block Adjustment of CBERS-2B HRC Imagery Combining Control Points and Lines[J]. Photogrammetrie-Fernerkundung-Geoinformation, 2012, 2012(2): 129-139. |
| [12] | SHAO Yongshe, LI Jing, ZHANG Shaoming, et al. Rectification Methods Based on Line Features for SPOT Imagery[J]. Journal of Tongji University: Natural Science, 2010, 38(8): 1249-1254. (邵永社, 李晶, 张绍明, 等. 基于线特征的SPOT影像几何纠正方法[J]. 同济大学学报: 自然科学版, 2010, 38(8): 1249-1254.) |
| [13] | YUAN Xiuxiao,CAO Jinshan. Theory and Method of Precise Object Positioning of High-resolution Satellite Imagery[M]. Beijing: Science Press, 2012. (袁修孝, 曹金山. 高分辨率卫星遥感影像精确对地目标定位理论与方法[M]. 北京: 科学出版社, 2012.) |
| [14] | LIU Jun, ZHANG Yongsheng, WANG Donghong.Precise Positioning of High Spatial Resolution Images Based on RPC Models[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 30-34. (刘军, 张永生, 王冬红. 基于RPC模型的高分辨率卫星影像精确定位[J]. 测绘学报, 2006, 35(1): 30-34.) |
| [15] | GRODECKI J, DIAL G. IKONOS Geometric Accuracy[C]//Proceedings of ISPRS Working Groups on High Resolution Mapping from Space 2001.Hanover:[s.n.], 2001(on CD-ROM). |
| [16] | ROBERTSON B C. Rigorous Geometric Modeling and Correction of QuickBird Imagery[C]//Proceedings of International Geoscience and Remote Sensing Symposium.Toulouse: IEEE, 2003(on CD-ROM). |
| [17] | YUAN Xiuxiao, LIN Xianyong. A Method for Solving Rational Polynomial Coefficients Based on Ridge Estimation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1130-1133. (袁修孝, 林先勇. 基于岭估计的有理多项式参数求解方法[J]. 武汉大学学报: 信息科学版, 2008, 33(11): 1130-1133.) |
| [18] | TAO C V, HU Y, JIANG W. Photogrammetric Exploitation of IKONOS Imagery for Mapping Applications[J]. International Journal of Remote Sensing, 2004, 25(14): 2833-2853. |
| [19] | FRASER C S, DIAL G, GRODECKI J. Sensor Orientation[JP] via RPCs[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 182-194. |
| [20] | TAO C V, HU Y. 3D Reconstruction Methods Based on the Rational Function Model[J]. Photogrammetric Engineering & Remote Sensing, 2002, 68(7): 705-714. |
| [21] | SCHENK T. From Point-based to Feature-based Aerial[JP] Triangulation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 58(5-6): 315-329. |
| [22] | ZHANG Zuxun, ZHANG Yongjun, ZHANG Jianging, [JP]et al. Photogrammetric Modeling of Linear Features with Generalized Point Photogrammetry[J]. Photogrammetric Engineering & Remote Sensing, 2007, 74(9): 1119-1127." |