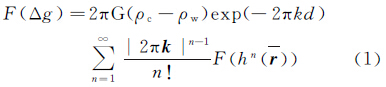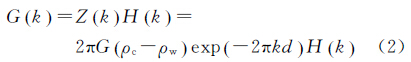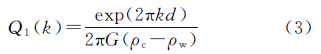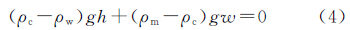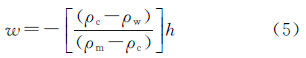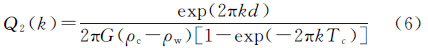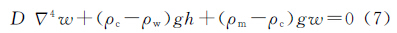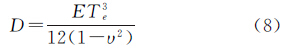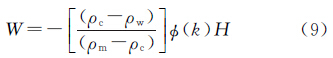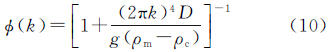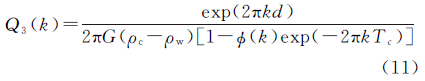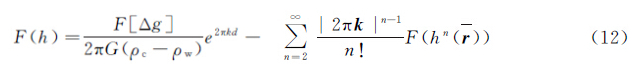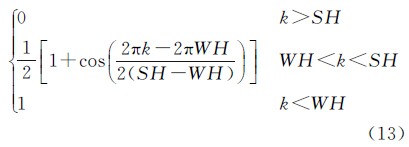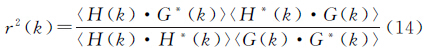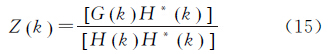2. 信息工程大学地理空间信息学院,河南 郑州 450001;
3. 西安测绘研究,陕西 西安 710054;
4. 地理信息工程国家重点实验室, 陕西 西安 710054
2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Stake Key Laboratory of Geo-information Engineering, Xi'an 710054, China
1 引 言
利用卫星测高技术,可以反演获得高精度的海面重力异常[1, 2]。重力异常综合反映了地下各物性的界面起伏与岩性的不均匀变化,由其反演出的界面变化有助于地质勘探、水准面精化和水下导航等方面的研究[3, 4, 5]。海洋空间重力异常和深度数据在一定波段内具有高度相关性[6],两者的频谱关系可通过“导纳”来描述。导纳应用于重力异常的实践始于20世纪70年代,文献[7]导出了基于傅里叶变换的频率域重力异常正演公式,提出了计算由于非线性和不均匀质体层引起场元扰动的新方法。文献[8]将之推广成迭代形式并做了二维计算,引入了不稳定的向下延拓因子并设计了低通滤波器以保证迭代计算的收敛,这种做法在消除高频震荡的同时对有效信号产生一定的抑制作用,因而会造成反演精度的下降。文献[9]采用交叉谱技术,对皇帝海山链的重力和海底地形剖面进行了计算,对未补偿导纳函数和顾及Airy补偿的导纳函数进行了简要介绍并推导出了顾及挠曲补偿的导纳函数,该函数可以通过海山链的海底地形预测出海面重力变化的大小,预测精度达到15×10-5m/s2。文献[10]在Parker公式和Watts 3个板块理论模型的基础上避开了关于构造补偿的假设,根据海域内重力和海底地形之间的变化关系推估海底地形,但其缺陷在于低估了复杂地形和较高海山的峰值,故不适用于判定导航时的危险区域。文献[11]综合利用卫星测高重力异常、船测水深、ETOPO5模型和GMT海岸线数据建立了南海海底地形模型,该模型以ETOPO5模型为基础,尝试通过频谱关系改善精度,但是效果并不明显。文献[12]给出了海底地形起伏与垂直重力梯度异常之间的导纳函数关系,联合船测海深和垂直重力梯度异常构建了全球海底地形模型。
皇帝海山链位于北太平洋,该海域存在间断的海底山、环礁、浅滩、海隆和暗礁,是国内外地球物理学家们开展板块模型研究的热点区域[13, 14, 15],他们对该海域地质构造的一系列研究为导纳法反演海底地形提供了一定的理论和技术支持。本文以该海域为研究对象,对重力异常和海底地形的相关性进行了分析,采用均衡响应函数法得到了皇帝海山链的平均地壳厚度和有效弹性厚度参数,采用移去恢复方法,得到了顾及挠曲补偿的导纳方法和未补偿导纳方法推估的皇帝海山链海底地形模型。基于上述方法,前人在不同海域已经成功实现了海底地形反演,然而对于其中涉及的物理参数求取、截断波长选择、滤波器设计以及不同方法反演的海深模型精度比较等均未详细说明,本文对上述问题进行了详细阐述并给出了反演模型的精度评定结果。常密度的三维密度界面反演方法在本文中也有试算,但由于是浅海区域,迭代计算未对结果有较大改善,不作为研究重点。
2 基本理论 2.1 导纳理论“导纳”描述了重力异常和地形的频谱关系,导纳函数具有线性、各向同性和空间不变性。1973年,Parker将快速傅里叶变换引入位场理论,大大提高了密度界面反演的计算速度[7]。该公式基于未补偿的海深模型,令G为地球引力常数;ρc为海底洋壳密度;ρw为海水密度;d为平均海深,则在频域内重力异常和海底地形的关系可以表示为
式中,k为(kx,ky)=(1/λx,1/λy),(kx,ky)和(λx,λy)为x和y方向的频率和波长;F为傅里叶变换;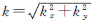 为圆频率。
为圆频率。当海底地形负荷的波长小于地壳的弹性厚度时,式(1)中的第1项起主要作用,它仅取决于平均海深,此时重力异常和海底地形之间是线性关系,公式为
式中,G(k)和H(k)分别为重力异常和水深的傅里叶变换,Z1(k)为导纳函数。Z1(k)中的2πG(ρc-ρw)是布格常数,exp(-2πkd)是向上延拓(从海底到海面)因子,对式(2)进行逆变换,可以通过卫星测高重力异常计算海底地形,在频率域内该导纳函数为
式(3)为未考虑补偿模型的导纳函数关系式。研究表明,大尺度的海底地形特征都可以用地壳均衡补偿理论[16]来解释,该理论描述了海底地形、地下质体层和重力异常的关系。挠曲均衡是Airy提出的均衡理论的广义形式[17],根据该理论,海底地形浮于密度较大的流体岩浆上面,海山越高沉下去越深,挠曲模型则考虑了岩石圈的弹性力,引进区域补偿代替局部补偿,将地形质量作为一种加在不断裂而有弹性的地壳层上的负荷。挠曲理论最早由Barrel于1914年提出,后人将该理论应用于实践并不断完善[18, 19, 20, 21, 22]。
根据Airy模型,海山和地形起伏造成的海底过剩质量反映在莫霍面上表现为“补偿根”的出现,令h为地形高,补偿根厚度为w,由漂浮的平衡条件为
式中,ρm为莫霍面下的地幔密度;g为重力加速度。由式(4)可得利用式(2)和式(4)得到由于h和w引起的重力异常变化,在频率域上求解,得到顾及Airy补偿的导纳函数表达式为
式中,Tc为平均地壳厚度。挠曲均衡理论考虑到了岩石圈弹性力对莫霍面形变w的抵制作用,抵制力用挠曲刚度D表示,形变方程为 式中,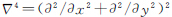 ;D为岩石圈的挠曲刚度,它与岩石圈的有效弹性厚度Te有关,即
式中,υ为岩石圈的泊松比;E为弹性模量。对其进行傅里叶变换,即
式中,ψ(k)表达式为
式中,g为平均重力加速度,结合式(7)、式(9)和式(10)可得
;D为岩石圈的挠曲刚度,它与岩石圈的有效弹性厚度Te有关,即
式中,υ为岩石圈的泊松比;E为弹性模量。对其进行傅里叶变换,即
式中,ψ(k)表达式为
式中,g为平均重力加速度,结合式(7)、式(9)和式(10)可得
当D=0时,挠曲导纳模型变为Airy导纳模型(式(6))。文献[8]提出,将Parker公式的级数展开后提出第1项,可以写成迭代形式,即
式(12)为常密度模型下的三维位场反演公式,迭代计算时首先令h(0)=0,Δg为由海底地形变化所引起的重力异常值,根据式(12)第1项推出h(1)(&rtilde;),然后代入式(12)右端,继而得到h(2)(&rtilde;),依次类推,直到h(n)(&rtilde;)和h(n-1)(&rtilde;)之差小于给定阈值,便得到最终的海底地形。
由式(3)、式(6)、式(11)、式(12)可以看出,导纳函数和地幔密度、海底洋壳密度、地壳密度、地壳厚度、岩石圈挠曲刚度、有效弹性厚度相关。
2.2 滤波器设计受向下延拓因子e(2πkd0)的影响,模型的高频分量很不稳定,有必要采用低通滤波进行处理。本文采用文献[8]设计的余弦低通滤波器得到了良好效果,即
式中,WH为低通波数;SH为高截断波数。 2.3 重力和海底地形的相关分析当已知某海域的重力异常和海底地形时,就可以采用时间序列的分析技术对两者关系进行研究[23]。频率域内,重力异常和海底地形相关估计r的最小二乘解为
式中,G(k)为重力异常的傅里叶变换;H(k)为海底地形的傅里叶变换;*为复数共轭;〈〉表示括号内两项谱乘积的实部在(k1-Δk≤k≤ki+Δk)环带内的均值。图 1示出了重力异常和海底地形的相关关系,不难看出,在20~300 km波长范围内重力异常和海底地形的相关系数最高。波长小于20 km,两者相关性很弱,这是因为,受向上延拓因素影响,重力异常的信号—噪声比很小,所谓信号是指海底地形变化对海面重力异常造成的影响量大小,用该波长段的数据反演海底地形是不“安全”的。同时,在长波段受均衡改正影响,海底地形变化不会对重力异常作出任何贡献,长波段地形的反演通常对船测水深控制点建立格网模型,采用低通滤波进行处理。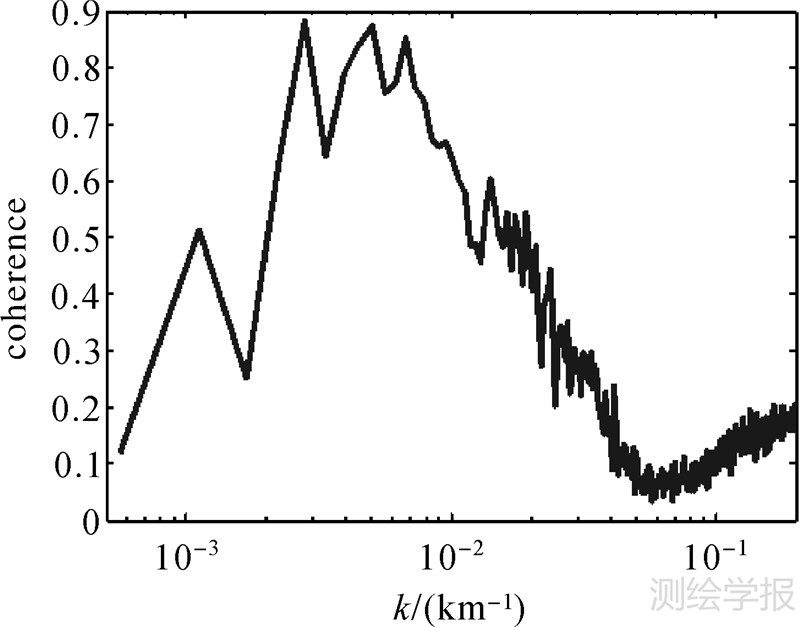 |
| 图 1 重力异常和海底地形的相关关系 Fig. 1 Coherence between gravity anomaly and bathymetry |
研究范围位于162°E—178°E,32°N—48°N之间,本文使用的船测水深数据来源于美国地球物理中心(NGDC)。NGDC拥有自21世纪50年代以来不同时期的海洋深度测绘数据,如图 2所示,图中红色的点为水深控制点,共计58 483个,将其格网化后经滤波处理得到反演海深模型的长波项,图中黄色的点为检核点,共计8355个,用来评估精度,控制点和检核点不重合。空间重力异常来自于丹麦科技大学空间中心1′分辨率的DTU10模型,如图 3所示,经与实测重力异常比较,两者差异的均值为0.39×10-5m/s2,标准差为3.82×10-5m/s2,最大值为36.89×10-5m/s2,船测水深控制点的重力异常由该模型插值得到。作为比较,本文也使用到了NGDC于2008年发布的1′分辨率的全球地形数据(ETOPO1)模型,该模型中的海洋深度数据来源于日本海洋地理数据中心(JOC)、美国地球物理中心(NGDC)、里海环境计划(CEP)和地中海科学委员会(CIESM)等组织,上述组织将不同海域的船载多波束测深数据格网化为不同分辨率大小的模型或将海洋等深模型数字化,而后提供给NGDC,NGDC根据需要对其统一编辑和评价,数据采用WGS-84坐标系统,各组织的数据提供情况如表 1所示。
 |
| 图 2 船测航迹分布 Fig. 2 Distribution of shipborne tracks |
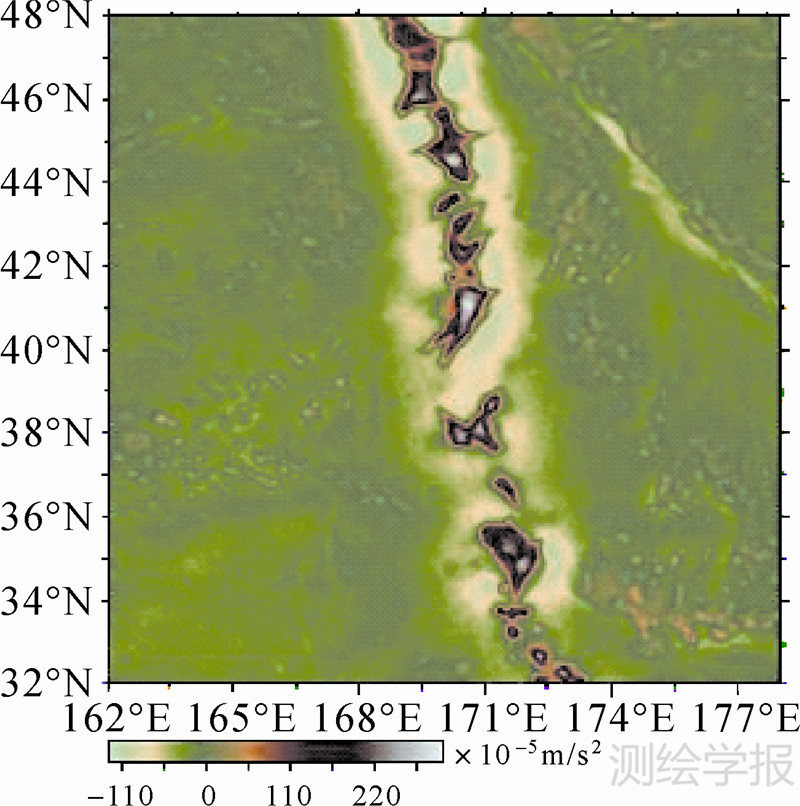 |
| 图 3 测高自由空间重力异常 Fig. 3 Altimetry-derived gravity anomalies |
| 来源 | 年份 | 数据类型 | 分辨率 | 坐标系 |
| JODC | 水深测量数据的格网化结果 | 0.5 km | WGS-84 | |
| NGDC | 2006 | 多波束测深数据的格网化结果 | 7″ | WGS-84 |
| CEP | 1999 | 等深模型数字化 | 1′ | WGS-84 |
| CIESM | 2005 | 多波束测深数据的格网化结果 | 0.5 km | WGS-84 |
挠曲导纳模型需要顾及地壳厚度和有效弹性厚度参数,采用均衡响应函数法,将船测水深格网化作为初始的水深模型,将DTU10作为初始的重力异常模型。重力异常和海底地形的观测导纳函数估计公式为
参数的确定需要重点考虑低频部分。经计算,皇帝海山链的地壳厚度参数为13 km,有效弹性厚度参数为13 km。
4 反演计算Airy模型是挠曲模型的特殊形式,本文不采用Airy导纳模型进行反演计算。三维位场理论经多次迭代试算得到的海深模型与初始模型差别不大,与未补偿导纳方法的反演结果相近,也不作为研究重点。本文采用未补偿导纳模型和顾及挠曲补偿的导纳模型两种方式反演海底地形。需要注意的是,针对重力异常卷积和反卷积计算涉及的边沿效应问题,在实际计算中需向四周扩展2°的面积范围,而后截断处理。
4.1 海深模型的反演重力异常仅包含了海底地形一定波段范围内的信息量,采用移去恢复程序建立海底地形模型,步骤如下。
(1) 截断波长的选择。考虑到重力异常和海底地形的相关性以及导纳函数呈线性的频段,采用未补偿导纳模型计算时设定截断波长为15~120 km;根据2.3节的相关性分析,采用挠曲导纳模型理论计算时设定截断波长为15~200 km,地壳厚度参数为13 km,岩石圈有效弹性厚度参数为13 km。
(2) 将研究海域船测水深控制点数据格网化,采用高斯滤波函数分别得到200 km和120 km长波截断下的参考海深模型,参考海深模型均值即为平均海深d。
(3) 将参考重力异常模型从观测重力异常模型中移去得到小于200 km和120 km波长的残余重力异常模型,由于残余重力异常模型的高频分量存在噪声影响,因而采用15 km波长的高斯函数进滤波处理。
(4) 将波长范围在15~200 km的残余重力异常模型采用顾及挠曲导纳模型的方法进行计算,得到波长在15~200 km范围的残余水深;将波长范围在15~120 km的残余重力异常模型采用未补偿导纳模型的方法进行计算,得到波长在15~120 km范围的残余水深。
(5) 将不同波长段的残余水深与相应的参考水深叠加,得到顾及不同导纳模型的皇帝海山链的海底地形。为方便统计,将顾及挠曲补偿的海深模型称为模型1,将采用未补偿导纳反演的海深模型称为模型2。
图 4示出了皇帝海山链的两个反演海深模型和ETOPO1模型,可以看出,在39°N、174°E附近,反演海深模型显示出了一条沿东北走向的海隆地形,该海隆地形在ETOPO1模型中未出现。图 5示出了两个反演海深模型和ETOPO1模型之差。可以看出,本文反演的两个海深模型差别不大,但与ETOPO1模型存在较大差别,其最大差值甚至高达1600 m左右,出现较大差值的海域大多分布有海山和海隆。
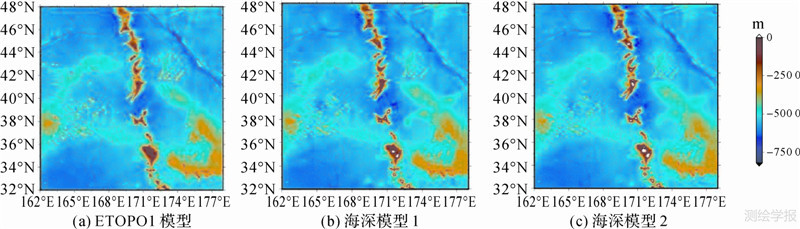 |
| 图 4 海底地形模型 Fig. 4 The bathymetry models |
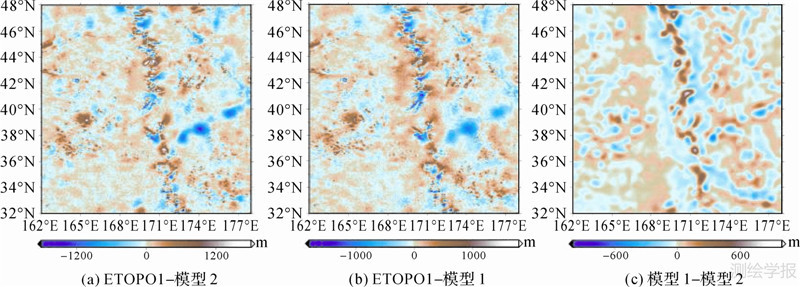 |
| 图 5 模型之间的差异 Fig. 5 The differences between models |
4.1节采用带通滤波移去恢复,最终得到15 km尺度的平均格网模型,对反演模型的精度估计并非采用全频带的实测海深模型去评价,原因在于并不存在如此多的实测海深数据去构建出一个完整的模型,相反,正是由于实测海深数据的稀少性,笔者才得以尝试通过海面重力异常反演出具备足够精细尺度的深度格网模型。如上文所述,本文采用了8355个离散的船测检核点对模型精度进行评估。
将3个海深模型在船测检核点上插值计算,得到插值水深与实际水深之较差。表 2示出了3个海深模型的检核比较统计结果,可以看出,本文反演的两个海深模型相对精度在6%左右,略低于ETOPO1模型;顾及挠曲补偿的海深模型精度低于未补偿导纳方法反演的海深模型。
| 模型 | Min/m | Max/m | Mean/m | STD/m | 相对精度 /(%) |
| ETOPO1 | -4 281.8 | 4 624.9 | 13.2 | 269.1 | 5.1 |
| 模型1 | -3 753.7 | 5 105.3 | 29.4 | 358.9 | 6.8 |
| 模型2 | -3 537.1 | 4 921.8 | 21.0 | 326.4 | 6.2 |
图 6(a)展示出了海深模型1的船测点较差结果统计直方图,图 6(b)在船测检核点位置示出了相对精度的绝对值统计结果。可以看出,大部分海域的相对精度较高,但在海山链以及两侧海隆区,点位相对精度较差。图 6(c)示出了较差结果、相对精度与海深的关系,较差结果没有呈现出明显的水深层分布特征,深海地区反演结果的相对精度明显好于水深浅于3000 m的海域。
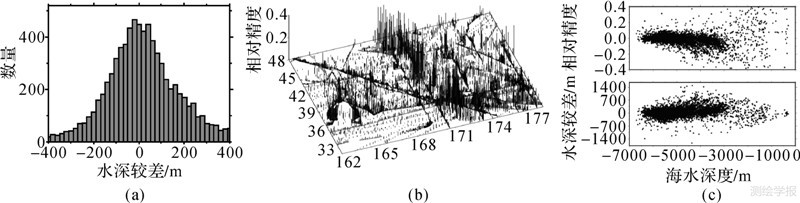 |
| 图 6 海深模型1的精度评估 Fig. 6 Precision estimation of bathymetry model one |
图 7以同样方式示出了海深模型2的船测检核点精度统计信息,与模型1情况基本一致,且略优于海深模型1。
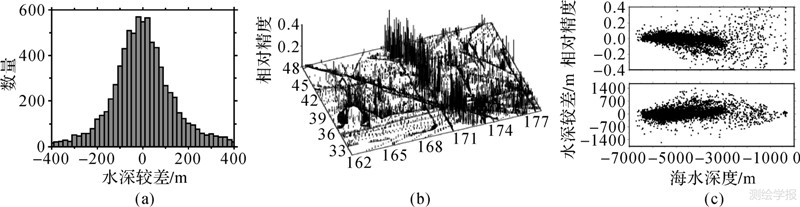 |
| 图 7 海深模型2的精度评估 Fig. 7 Precision estimation of bathymetry model two |
本文将相对精度大于40%的点定为粗差,为了分析粗差产生的原因,有必要单独研究。图 8(a)、(b)分别示出了模型1和模型2的粗差点分布,模型1产生粗差点229个,占总数的2.7%,模型2产生粗差点185个,占总数的2.2%。可以看出,粗差点主要集中在海山链沿线,说明由于该部分海域地形起伏变化剧烈,对反演模型精度造成了很大影响。
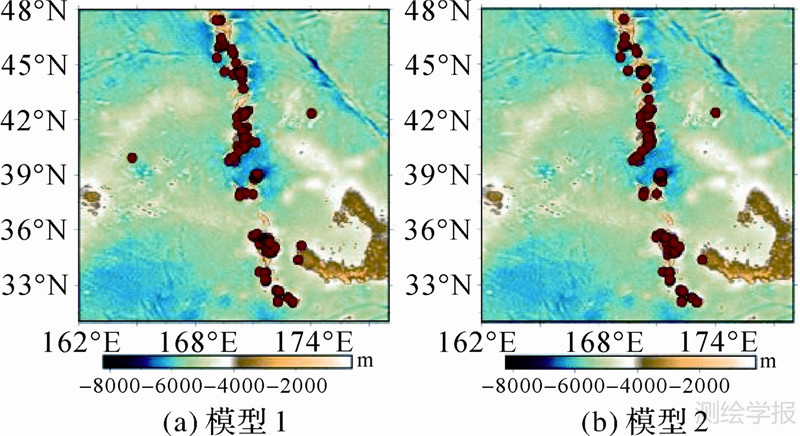 |
| 图 8 粗差点分布 Fig. 8 The distribution of gross error points |
由上文可知,ETOPO1模型中未显现的海底地形起伏在本文反演模型中有清晰的显示,但本文的反演模型精度略低于ETOPO1模型。对反演模型精度造成影响的来源主要有3个方面:①部分用作检核的船测点质量不高,但使用时难以完全去除。②浅海地区重力异常受噪声影响,反演质量下降。③重力异常的导纳理论存在自身局限。这种局限性主要体现为:首先,由于需要一定数量的船测水深或先验模型获取海深长波项,因此长波项精度受先验模型精度、船测点数量分布等的影响较大;其次,参与导纳计算的地壳厚度、有效弹性厚度等参数仅为区域平均值,难以与局部海域做到严密吻合。图 9展示出了采用挠曲模型得到的残余海深和残余重力异常在空间域内的关系图,反映出两者具有良好的线性关系,但实际上海底地形复杂多变,其在空间域内和重力异常并非是完全严密的线性关系。针对上述情况,文献[10]将短波船测水深和短波重力异常之比定义为比例因子,使用移去恢复法将短波项和长波项叠加得到海底地形,受船测点数量和分布限制,能否有效提高精度还有待进一步研究。
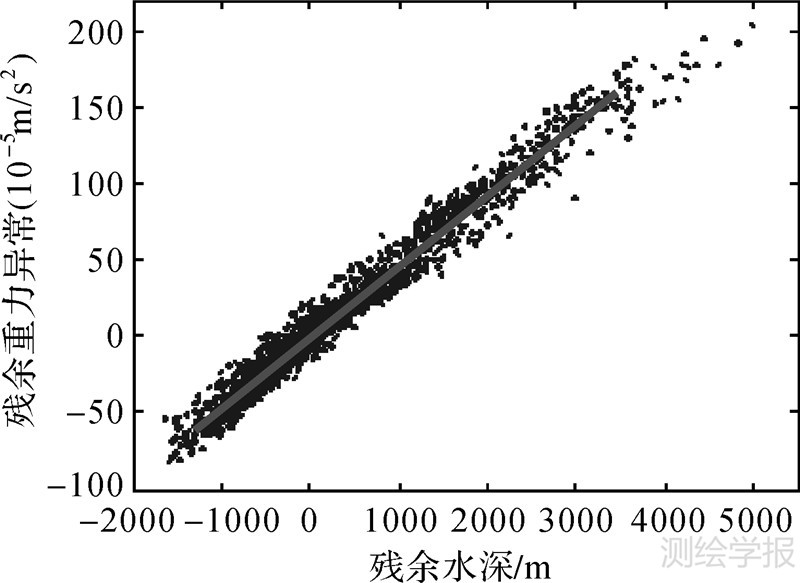 |
| 图 9 空间域内残余重力异常残余海深的关系 Fig. 9 The relationship between the residual depth and residual gravity anomalies in space domain |
根据重力异常的导纳理论,本文采用未补偿的导纳方法和顾及挠曲补偿的导纳方法反演了皇帝海山链的海底地形模型,并进行了精度评价,得到以下初步结论。
(1) 海底地形和重力异常在20~300 km波长范围内相关系数较高,采用顾及挠曲补偿的导纳方法,能够实现15~200 km左右波长范围的地形反演,对计算海深模型长波项所需的离散船测控制点分布、波长间距和数量要求不高;未补偿的导纳方法能够实现15~120 km左右波长范围的地形反演,由于长波项截断波长较小,对离散船测水深控制点的分布、波长间距和数量要求较高。
(2) 顾及挠曲补偿的导纳方法涉及诸如地壳厚度和有效弹性厚度等参数的求取,通常使用计算得到的区域平均值作为代替,对反演结果会产生一定影响,且反演出的模型精度略低于未补偿导纳海深模型。
(3) 本文反演的两个海深模型在深海地区的相对精度优于浅海海域,相对精度下降的主要原因在于海山链和海隆的存在,经ETOPO1模型比较和检核点精度统计,其中的绝大部分粗差分布于海山链沿线。
(4) 采用重力异常的导纳理论反演海底地形能够刻画出ETOPO1模型中未显现的海底地形细节,但反演精度受其自身局限的影响,下一步将结合文献[10]方法,开展进一步研究。
| [1] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 179-184. (黄谟涛, 翟国君, 管铮, 等. 利用卫星测高数据反演海洋重力异常研究[J]. 测绘学报, 2001, 30(2): 179-184.) |
| [2] | LI Jiancheng, NING Jinsheng, CHEN Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/Poseidon, ERS2 and Geosat Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 197-202. (李建成, 宁津生, 陈俊勇, 等. 联合TOPEX/Poseidon, ERS2和Geosat卫星测高资料确定中国近海重力异常[J]. 测绘学报, 2001, 30(3): 197-202.) |
| [3] | LI Shanshan, WU Xiaoping, ZHANG Chuanding, et al. Regional Quasi-geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly's Gradient Term[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 510-516. (李姗姗, 吴晓平, 张传定, 等. 顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J]. 测绘学报, 2012, 41(4): 510-516.) |
| [4] | WANG Hubiao, WANG Yong, XU Daxin, et al. Distribution of Navigation Value about Vertical Gradient and Its Navigability Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 364-369. (王虎彪, 王勇, 许大欣, 等. 重力垂直梯度导航值特征分布与可导航性分析[J]. 测绘学报, 2010, 39(4): 364-369.) |
| [5] | ZENG Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005. (曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005.) |
| [6] | SIEMENS C W. On Determining the Depth of the Sea Without the Use of the Sounding-Line[J]. Philosophical Transactions of the Royal Society of London, 1876, 166: 671-692. |
| [7] | PARKER R L. The Rapid Calculation of Potential Anomalies[J]. Journal of the Royal Astronomical Society, 1973, 31(4): 447-455. |
| [8] | OLDENBURG D W. The Inversion and Interpretation of Gravity Anomalies[J]. Geophysics, 1974, 39(4): 526-536. |
| [9] | WATTS A B. An Analysis of Isostasy in the World's Oceans: 1. Hawaiian-Emperor Seamount Chain[J]. Journal of Geophysical Research, 1978, 83(B12): 5989-6004. |
| [10] | SMITH W H F, SANDWELL D T. Bathymetric Prediction from Dense Satellite Altimetry and Sparse Shipboard Bathymetry[J]. Journal of Geophysical Research, 1994, 99(B11): 21803-21824. |
| [11] | HWANG C. A Bathymetric Model for the South China Sea from Satellite Altimetry and Depth Data[J]. Marine Geodesy, 1999, 22(1): 37-51. |
| [12] | HU Minzhang, LI Jiancheng, XING Lelin. Global Bathymetry Model Predicted from Vertical Gravity Gradient Anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 556-565. (胡敏章, 李建成, 邢乐林. 由垂直重力梯度异常反演全球海底地形模型[J]. 测绘学报, 2014, 43(6): 559-565.) |
| [13] | MOORE J G. Relationship Between Subsidence and Volcanic Load, Hawaii[J]. Bulletin Volcanologique, 1970, 34(2): 562-576. |
| [14] | WATTS A B. On Geoid Heights Derived from Geos 3 Altimeter Data Along the Hawaiian-Emperor Seamount Chain[J]. Journal of Geophysical Research, 1979, 84(B8): 3817-3826. |
| [15] | SUZANNE N L, SANDWELL D T, SMITH W H F. Three-Dimensional Estimation of Elastic Thickness under the Louisville Ridge[J]. Journal of Geophysical Research, 2000, 105(B6): 13239-13252. |
| [16] | HEISKANEN W A, VENING MEINESZ F A. The Earth and Its Gravity Field[M]. New York: McGraw-Hill, 1958. |
| [17] | AIRY G B. On the Computation of the Effect of the Attraction of Mountain-Masses, as Disturbing the Apparent Astronomical Latitude of Stations in Geodetic Surveys[J]. Philosophical Transactions of the Royal Society of London, 1855, 145: 101-104. |
| [18] | BARRALL J. The Strength of the Earth's Crust[J]. The Journal of Geology, 1914, 22(5): 441-468. |
| [19] | VENING MEINESZ F A. Gravity over the Hawaiian Archipelago and over the Madeira Area: Conclusions about the Earth's Crust[M]. [S.l.]: Proc Kon Ned Akad Wetensia, 1941. |
| [20] | GUNN R. A Quantitative Study of Isobaric Equilibrium and Gravity Anomalies in the Hawaiian Islands[J]. Journal of the Franklin Institute, 1943, 236(4): 373-390. |
| [21] | WALCOTT R I. Flexure of the Lithosphere at Hawaii[J]. Tectonophysics, 1970, 9(5): 435-446. |
| [22] | WATTS A B, Bodine J H, Ribe N M. Observations of Flexure and the Geological Evolution of the Pacific Ocean Basin[J]. Nature, 1980, 283(5747): 532-537. |
| [23] | LEWIS B T R, DORMAN L M. Experimental Isostasy: 2. An Isostatic Model for the USA Derived from Gravity and Topographic Data[J]. Journal of Geophysical Research, 1970, 75(17): 3367-3386. |