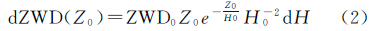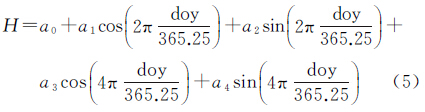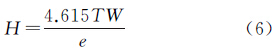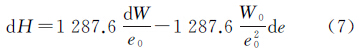2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079;
3. 地球空间信息技术协同创新中心,湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
1 引 言
水汽是地球大气中一种非常活跃多变的组分,它的含量虽然不多,但在一系列时空尺度的大气过程中发挥着关键作用。水汽的分布与流动直接与降水、旱涝灾害等密切相关;水汽的平流和大气环流所带来的潜热是地球南北半球能量平衡的关键因素[1];水汽也是地球大气中最丰富的温室气体,大气中水汽含量的变化对于气候变化有着重要影响[2]。另外,水汽也是能量传播的介质,能够吸收、折射多波段的电磁波[3],会对卫星导航定位[4]和SAR成像产生重要影响[5]。
水汽主要集中在低大气层,对流层中的水汽约占总水汽含量的99%,高度在2 km以下的水汽约占总水汽含量的一半左右[7]。水汽在大气中的含量较少(0~4%),却是大气中最活跃多变的成分,也是最难以描述的气象参数之一[8]。水汽标高是反映对流层水汽垂直分布特征的一个重要参量,其物理意义是在假定水汽密度在垂直方向遵循指数分布的前提下,水汽密度(水汽压、比湿)减少为原值的36.7%(1/e)时所需要的高度增量[9, 10]。在此定义下,水汽标高亦即指数函数随高度的递减系数(见式(1)),当水汽标高已知时,水汽的垂直分布也就知道了,因此水汽标高是反映水汽垂直分布的一个重要参量。文献[9, 11]分别于1977年和1981年利用探空数据统计了意大利Po Valley地区水汽标高的变化信息,指出该地区水汽标高的变化介于1.68~1.92 km之间,并且有冬季大、夏季小的特征。文献[12]利用新疆地区12个探空站10 a的气象资料,得到该地区的平均水汽标高为2.17 km。文献[7]利用微波辐射计4 a中晴天的观测数据分析了合肥地区标高的季节变化和日变化特征[7]。
在笔者之前的工作中,为了准确地对全球导航卫星系统信号穿越对流层时的天顶湿延迟(zenith wet delay,ZWD)进行高程改正,在假定ZWD在垂直方向遵循指数变化的情况下,需要将水汽标高的倒数作为高程改正系数[13]。在对流层层析模型的垂直约束构建中,也需要水汽标高来表征和约束湿折射率(水汽密度)的垂直分布[14, 15, 16]。为了解决上述问题中对水汽标高的需要,本文首先对水汽标高的时间序列进行了频谱分析,然后根据水汽标高的时间特性构建了适合表达水汽标高的数学模型。为了顾及水汽标高的地理差异,在全球范围内以1°×1°的分辨率拟合了模型系数,最终构建了一个全球适用的水汽标高经验模型,并对模型进行了检验。该模型所给出的值实质上是水汽密度(或湿折射率亦或天顶湿延迟)在天顶方向遵循指数分布规律假定时的垂直递减率(式(1)中的H),反映了水汽的垂直分布情况,这对于气象学研究是有重要意义的。同时,该模型也可用于构建层析湿折射率时的垂直约束和天顶对流层湿延迟的高程改正。
2 水汽标高的计算 式中,ρz是相对地表z高度处的水汽密度; ρ0是地表水汽密度; H为水汽标高。类似的,GNSS信号的天顶湿延迟以及无线电信号的湿折射率也可以用式(1)的形式进行表达,仅需将式中的水汽密度换为天顶湿延迟或湿折射率。为了说明水汽标高误差对天顶湿延迟改正的影响,将式(1)对水汽标高求偏导,并将水汽密度换作天顶湿延迟,可得 式中,ZWD0为地表的天顶湿延迟;Z0为相对地表的高度;H0为水汽标高的近似值。假设ZWD0为200 mm、Z0为0.5 km、H0为2 km,则按照式(2),1 km的水汽标高误差可引起19.5 mm的ZWD估计误差,而且这些数值假设还是相对保守的,所以水汽标高的精度对于一些模型的天顶湿延迟的高程改正具有重要作用。根据文献[7]中的表述,水汽标高H可如下计算 式中,H是水汽标高,单位是km;W是指贯穿整层大气层的单位面积的垂直柱体中的水汽总量,单位为g/cm2;ρ0的单位是g/m3。ρ0可以通过以下公式计算 式中,e为地面水汽压(Pa);T为混合气体的绝对温度(K);Rv=0.461 5 J/(k·g),为水汽比的气体常数[17]。ECMWF可以在全球范围内以不高于0.125°×0.125°的分辨率提供多种气象参数,其中包括大气可降水量、露点温度和温度,这些数据可供我们计算地表水汽密度和水汽标高。文献[18—19]提供了精确的饱和水汽压计算公式,将露点温度带入Wexler公式即可得到水汽压。将ECMWF的大气可降水量化为以g/cm2为单位,露点温度换算为以Pa为单位的水汽压,就可以根据式(4)和式(3)计算水汽标高。
3 水汽标高的时间特性及GSH模型构建为了研究水汽标高的时间特性,利用第2节中的方法计算了全球1°×1°格网点上共计64 442个点上从2006年至2012年共计7年的水汽标高,并利用傅里叶变换的方法对水汽标高进行了频谱分析。图 1显示了部分点上的水汽标高时间序列以及傅里叶变换后得到的功率-周期图。图 1中绿色的点为图中对应位置上2006—2012年根据ECMWF数据计算的水汽标高,红色的线是对计算的水汽标高进行的函数拟合。
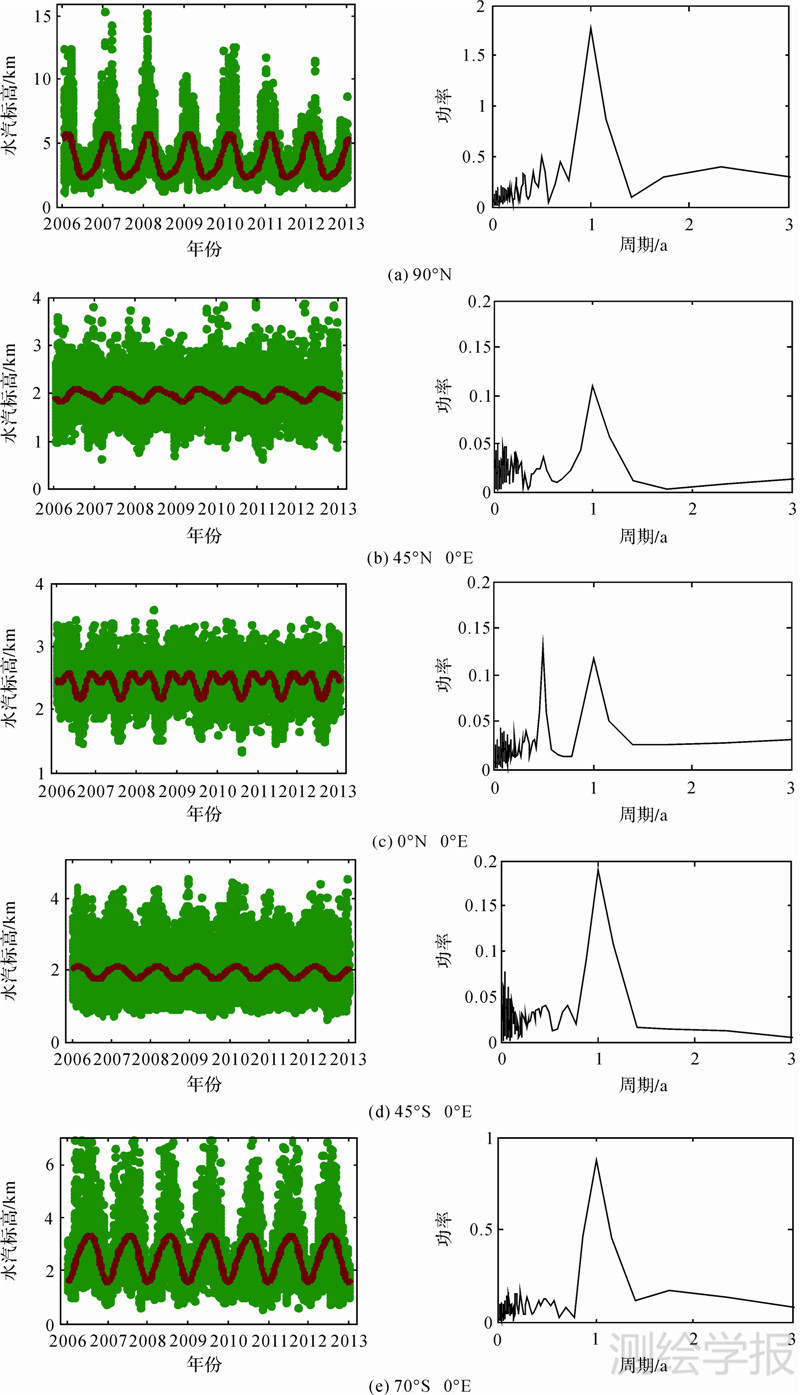 |
| 图 1 部分地点2006—2012年水汽标高的时间序列及功率—周期图 Fig. 1 Plots of time series of water vapor scale height and power versus period at some places during 2006 to 2012 |
由图 1可以看出水汽标高整体都呈现出一定的周期特性,以年周期和半年周期最为强烈。但不同地点又呈现出不同的周期特性,有的地区年周期特性显著,而半年周期特性很弱,而另外一些地方半年周期与年周期同样显著,甚至超越了年周期。为了同时兼顾水汽标高的年周期和半年周期特性,利用式(5)的三角函数来表达水汽标高的时间变化
式中,H为水汽标高;doy为年积日;a0、a1、a2、a3、a4为模型系数。需要说明的是,虽然在一些地区水汽标高只有微弱的半年周期特性甚至没有,但式(5)依然能够描述该地区的水汽标高,这是因为当水汽标高的半年周期特性很弱时,利用实测数据拟合式(5)时,系数a3和a4就会变得很小,甚至为0,此时式(5)自动退化为仅包含年周期特性的三角函数。该方法也常见于其他气象参数的建模,如全球气压温度模型GPT2[20]、加权平均温度模型[21]、对流层延迟改正模型[22, 23]等。将同一地点上多年的水汽标高观测值和对应的时间带入式(5),就可以将式(5)转换成以水汽标高为观测值,a0、a1、a2、a3、a4为未知数的线性方程,进而利用最小二乘法就可以解算得到a0、a1、a2、a3、a4。由于水汽变化较快,并且存在地理差异(这点可以从图 1中不同地点的水汽标高对比看出),因此式(5)需要针对特定的地点来拟合模型系数。为了在全球范围内构建水汽标高模型,利用ECMWF提供的2006—2012年的大气可降水量、露点温度和温度数据在1°×1°的格网点上分别拟合了式(5)的系数a0、a1、a2、a3、a4,进而建立了根据年积日计算水汽标高的全球水汽标高模型GSH。GSH模型以格网形式提供了全球1°分辨率的a0、a1、a2、a3、a4。在使用模型时需输入测站经纬度和观测的年积日,模型首先根据经纬度找出与测站最邻近的4个格网点,并根据这4个格网点上的a0、a1、a2、a3、a4计算得到4个水汽标高值,然后利用双线性内插得到测站位置处的水汽标高。 4 GSH模型的检验由于目前并没有全球适用的水汽标高模型,因此本文无法进行对比检验,只能利用2010年的无线电探空数据和2013年的ECMWF数据对GSH模型检验进行外符合检验。文中以无线电探空数据和ECMWF数据为参考值,首先在每一个探空站或每一个ECMWF格网点根据式(3)计算出水汽标高的值,这里称作观测值;然后利用GSH模型计算出测站或格网点对应位置对应时刻的模型值;最后利用模型值减去观测值得到二者的差值,计算每个站点或格网点上所有差值的偏差和均方根误差。将偏差和均方根误差作为评价模型精度和稳定性的指标,对模型的精度和稳定性进行分析讨论。
首先利用全球均匀分布的320个无线电探空站2010年全年的探空数据对GSH模型进行检验,探空高度小于15 km的数据被删除,统计了模型在每个探空站的偏差和均方根误差。结果显示GSH模型具有-0.19 km的偏差和1.81 km的均方根误差。图 2显示了探空站的分布以及GSH模型在各个站上的偏差和均方根误差。
 |
| 图 2 全球320个无线电探空站的分布及GSH模型在各个站上的偏差和均方根误差 Fig. 2 Global distribution of the 320 radiosonde stations and bias and RMSE of the GSH model at these stations |
由图 2可以看出GSH模型的精度分布呈现出局部集中,整体杂乱的特点,这主要是因为水汽变化很快,而水汽标高的变化更快,因此只有水汽变化特征比较接近的局部区域才能获得比较接近的精度。为了说明这一点,将式(3)和式(4)合并得到
以ECMWF 2012年的月平均数据计算得到的全球平均大气可降水量为1.8 g/cm2,平均地表温度为279 K,平均水汽压为1200 Pa,平均水汽标高为2.04 km。对式(6)进行全微分,根据误差传播率,很容易发现水汽标高受温度影响很小(即使误差10 K,对H的影响也不超过0.1 km),因此这里直接把温度固定为279 K。不考虑温度变化将式(6)全微分可得
式中,e0和W0为水汽压和大气可降水量的近似值。由于地球附近的水汽压变化很大,即使同一地点在不同时间也可以从几十帕变化到几千帕,故式(7)中第1项的影响明显要比第2项的大。当水汽压过小时,式(7)中第1项的系数就会很大,dH会变得对dW非常敏感。此时若水汽压为400 Pa,1 g/cm2的大气可降水量误差就可以引起超过3 km的水汽标高误差。因此水汽标高计算公式本身的精度受大气可降水量精度影响很大,水汽标高计算值本身就难以确保稳定的精度,进而导致GSH模型的精度也存在变化较大的现象。随后,利用ECMWF 2013年全年的大气可降水量数据、地表露点温度数据和地表温度数据计算了全球1°×1°格网点上的水汽标高,并将2013年的水汽标高作为参考值对GSH模型进行检验。图 3给出了模型值相对参考值的精度分布信息。
 |
| 图 3 利用2013年的ECMWF数据对GSH模型检验的精度分布信息 Fig. 3 Accuracy of the GSH model with respect to the ECMWF data in 2013 |
实际上,图 3并没有包含全部的64 442个点,有285个点的精度信息并没有显示。因为在这285个点上GSH模型计算的水汽标高值超过20 km,通常水汽一般分布在15 km以下的高度,20 km以上基本可以认为没有水汽,因此水汽标高出现在20 km以上本身就是不合理的。如前面所述,水汽标高对于大气可降水量非常敏感,大气可降水量的误差会被放大数倍甚至数十倍后引入水汽标高。再者,式(3)和式(4)是在假定水汽密度随高度呈指数递减的前提下推导出来,而实际中水汽密度并非严格遵循上述规律,式(1)仅是种近似表达。因此,计算公式的不严谨、测量本身难以避免的误差以及水汽标高对自变量的高度敏感性导致了水汽标高难以有很准确的计算值,而利用经验模型来拟合上述计算值必然也不会很完美,因此GSH模型在部分地区出现了超出实际情况的值。就图 3的整体情况来看,GSH模型基本在全球大部分地区取得了比较稳定的精度,除了南极地区、俄罗斯东北部等小部分地区,统计结果也显示GSH模型在全球范围内具有0.04 km的平均偏差和1.52 km的均方根误差。
图 2和图 3显示了GSH模型精度的地理分布,但从图 1可以看出水汽标高的季节性变化很大,因此有必要对GSH模型精度的季节性变化进行检验。这里利用2013年全年的ECMWF1°×1°的数据对GSH模型进行季节性检验。由于南北半球季节相反,在南半球和北半球分别进行检验,统计了GSH模型在每个月的偏差和均方根误差,结果如图 4所示。
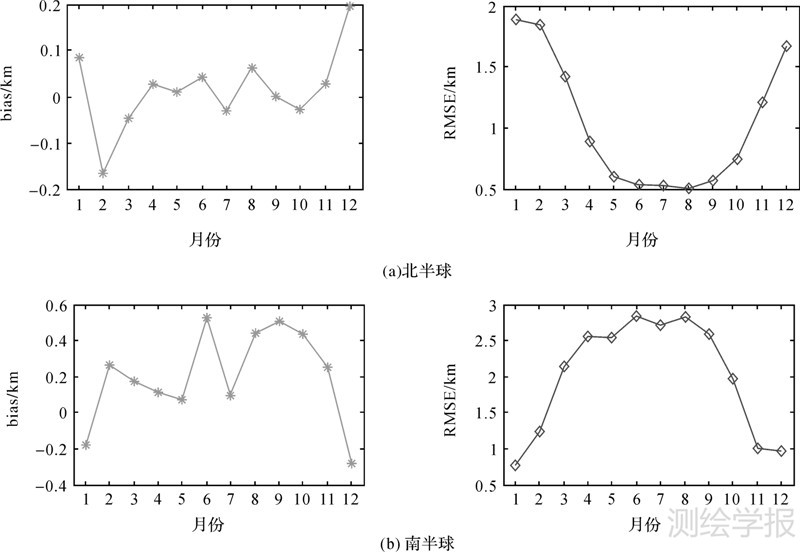 |
| 图 4 利用2013年的ECMWF数据对GSH模型进行的季节性检验 Fig. 4 Seasonal test results of GSH model with respect to the ECMWF data in 2013 |
从图 4可以看出,GSH模型的偏差和均方根误差在南半球要略大于北半球。在2013年的12个月份中,偏差的绝对值都不超过0.6 km,均方根误差的量值都不超过3 km。在北半球GSH模型的均方根误差在5—9月份很小,这是因为在这些月份中,北半球处于一年中温度最高的季节,由于地表水分蒸发强烈,在低大气层集中了大量的水汽,按照水汽标高的定义,此时的水汽标高将会下移,该现象可以从图 1的第一幅图显著看出。水汽标高的量值减少有利于模型获得较小的绝对误差,因此GSH模型在北半球的5—9月份出现了最小均方根误差。在北半球的冬春季节,由于蒸发效应减少,大气中的水汽变得稀疏,水汽标高将会上移,水汽标高的量值变大使得模型容易产生了较大的均方根误差。在南半球,GSH模型的精度在5—9月份产生了最大误差,在年初和年终出现了最小误差,与北半球的情况相反,这主要是南北半球季节相反导致的,在南半球年中时水汽标高的量值最大,而年初和年终时水汽标高很小,而水汽标高量值越大是容易引发较大的绝对误差的。
5 结 论水汽标高是一个反映水汽垂直分布特征的参数,也是GNSS天顶湿延迟高程改正、GNSS水汽层析中的一个辅助参数。本文在水汽时间序列呈现出年周期和半年周期特性的基础上,利用余弦函数来表达水汽标高的时变规律,进而构建了以经纬度和年积日为参数的GSH模型。经无线电探空数据和ECMWF数据的检验,GSH模型整体表现比较稳定,相对于无线电探空数据,GSH模型具有-0.19 km的偏差和1.81 km的均方根误差;相对于ECMWF数据,GSH模型具有0.04 km的偏差和1.52 km的均方根误差。
由于式(1)不能严格表达水汽的实际变化特征,进而得到的水汽标高计算公式不精确以及水汽标高对大气可降水量的高度敏感性和气象元素测量误差的存在,水汽标高的计算本身容易产生误差,进而导致构建的模型也会存在一定的误差,这是GSH模型在小部分地区出现异常情况的根本原因。
本文首次构建了一个全球水汽标高模型,出发点是为GNSS对流层天顶湿延迟改正以及GNSS水汽层析服务,但它本身也可为气象应用研究提供了水汽标高的参考值,相对于全球使用一个相同的水汽标高(~2 km)更具参考价值。
致谢:感谢ECMWF提供的气象数据以及IGRA提供的无线电探空数据。
| [1] | BEVIS M, BUSINGER S, HERRING TA, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801. |
| [2] | JACOB D. The Role of Water Vapour in the Atmosphere.A Short Overview from a Climate Modeller's Point of View[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(6-8): 523-527. |
| [3] | CHEN Junyong. On the Error Analysis for the Remote Sensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(2): 113-118. (陈俊勇. 地基GPS遥感大气水汽含量的误差分析[J]. 测绘学报, 1998, 27(2): 113-118.) |
| [4] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Extracting Precise Atmospheric Propaganda Delays from Multiple Reference Station GPS Networks[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 523-528. (张宝成, 欧吉坤, 袁运斌, 等. 多参考站GPS网提取精密大气延迟[J]. 测绘学报, 2012, 41(4): 523-528.) |
| [5] | QIAN Chuang, HE Changyong, LIU Hui. Regional Precise Troposphere Delay Modeling Based on Spherical Cap Harmonic Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 248-256. (钱闯, 何畅勇, 刘晖. 基于球冠谐分析的区域精密对流层建模[J]. 测绘学报, 2014, 43(3): 248-256.) |
| [6] | KOU Leilei, XIANG Maosheng. Effect of Temporal Variation of Atmospheric Refraction on Geosynchronous Circular SAR Focusing Performance[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 917-923. (寇蕾蕾, 向茂生. 大气折射率时间变化对地球同步轨道圆迹SAR聚焦性能的影响[J]. 测绘学报, 2014, 43(9): 917-923.) |
| [7] | LI Chao, WEI Heli, WANG Zhenzhu, et al. Statistical Study on the Scale Height of Atmospheric Water Vapor in Hefei Region[J]. Journal of Atmospheric and Environmental Optics, 2008, 3(2): 115-120. (李超, 魏合理, 王珍珠, 等. 合肥地区大气水汽标高变化特征的统计研究[J]. 大气与环境光学学报, 2008, 3(2): 115-120.) |
| [8] | ROCKEN C, VAN HOVE T, WARE R. Near Real-time GPS Sensing of Atmospheric Water Vapor[J]. Geophysical Research Letters, 1997, 24(24): 3221-3224. |
| [9] | TOMASI C. Determination of the Total Precipitable Water by Varying the Intercept in Reitan's Relationship[J]. Journal of Applied Meteorology, 1981, 20(9): 1058-1069. |
| [10] | REITAN C H. Surface Dew Point and Water Vapor Aloft[J]. Journal of Applied Meteorology, 1963, 2(6): 776-779. |
| [11] | TOMASI C. Precipitable Water Vapor in Atmospheres Characterized by Temperature Inversions[J]. Journal of Applied Meteorology, 1977, 16(3): 237-243. |
| [12] | ZHANG Xuewen. The Vertical Distribution Law of Vapor Pressure in Xinjiang, China[J]. Bimonthly of Xinjiang Meteorology, 2002, 25(4): 1-2, 14. (张学文. 新疆水汽压力的铅直分布规律[J]. 新疆气象, 2002, 25(4): 1-2, 14.) |
| [13] | SCHVLER T. The TropGrid2 Standard Tropospheric Correction Model[J]. GPS Solutions, 2014, 18(1): 123-131. |
| [14] | YU Shengjie, LIU Lintao, LIANG Xinghui. Influence Analysis of Constraint Conditions on GPS Water Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 492-496. (于胜杰, 柳林涛, 梁星辉. 约束条件对GPS水汽层析解算的影响分析[J]. 测绘学报, 2010, 39(5): 492-496.) |
| [15] | FLORES A, RUFFINI G, RIUS A. 4D Tropospheric [JP]Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae, 2000, 18(2): 223-234. |
| [16] | FLORES A, DE ARELLANO J V G, GRADINARSKY L P,[JP] et al. Tomography of the Lower Troposphere Using a Small Dense Network of GPS Receivers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(2): 439-447. |
| [17] | DAVIS J L, HERRING T A, SHAPIRO I I, et al. Geodesy[JP] by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1593-1607. |
| [18] | WEXLER A. Vapor Pressure Formulation [JP]for Water in the[JP] Range 0 to 100°C: A Revision[J]. Journal of Research of the National Bureau of Standards-A: Physics and Chemistry, 1976, 80A(5-6): 775-785. |
| [19] | WEXLER A. Vapor Pressure Formulation for Ice[J]. Journal[JP] of Research of the National Bureau of Standards-A: Physics and Chemistry, 1977, 81A(1): 5-20. |
| [20] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. [JP]GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073. |
| [21] | YAO Y B, ZHANG B, XU C Q, et al. Improved One-multi-parameter Models that Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperaturein Ground-based GPS Meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282. |
| [22] | LI W, YUAN Y B, OU J K, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132-2139. |
| [23] | YAO Yibin, HE Changyong, ZHANG Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227. (姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227.) |