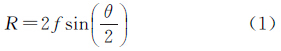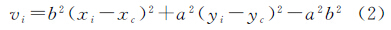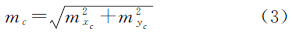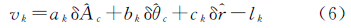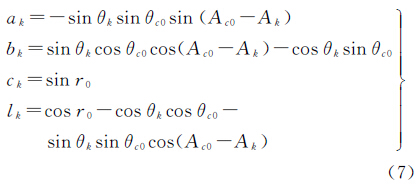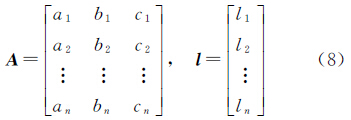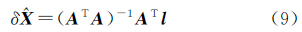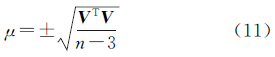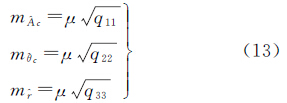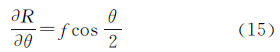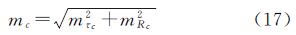2. 信息工程大学地理空间信息学院，河南 郑州 450001;
3. 郑州大学水利与环境学院，河南 郑州 450001
2. College of Geographic Spatial Information, Information Engineering University, Zhengzhou 450001, China;
3. College of Water Conservancy & Environmental Engineering, Zhengzhou University, Zhengzhou 450001, China
1 引 言
太阳敏感器是一种通过观测太阳方向矢量确定载体姿态的传感器，在航空航天领域应用极其广泛。美国勇气号和机遇号火星车上均搭载有高精度的太阳敏感器，用于确定车体的绝对航向，从而改正IMU随时间漂移带来的航向误差[1, 2, 3]。近地航天器上普遍搭载有太阳敏感器，用于航天器初始姿态的快速捕获[4]。太阳图像质心提取是利用太阳敏感器进行天文导航的关键技术之一，图像质心提取的精度直接决定了太阳敏感器的观测精度，进而影响载体的姿态确定精度。因此，如何精确、快速地提取太阳图像质心是近些年的研究热点。
太阳图像质心提取算法主要分灰度质心法和拟合法两类。灰度质心法包括固定阈值的灰度质心法[5]，基于直方图阈值分割的灰度质心法[6]，基于Otsu阈值分割的灰度质心法[7]等。拟合法首先采用边缘检测算法提取太阳图像的边缘点，然后采用最小二乘法对边缘点进行圆拟合，圆心即为太阳图像的质心。拟合法的关键是如何实现高精度的太阳图像边缘检测，文献[8]提出采用Sobel算子进行太阳图像边缘的粗检测，然后采用Zernike矩进行亚像素重定位，最后拟合圆心作为图像质心。其对实测太阳图像的处理结果显示，算法质心提取精度达到0.08 pixels。事实上，亚像素边缘检测算法很多，包括梯度法、插值法、拟合法、频谱分析法、矩法等几类[9, 10, 11, 12, 13, 14, 15]，均可应用于太阳图像边缘检测。此外，文献[16—17]分别针对电子经纬仪测日、测月定向问题，提出了基于水平角和高度角观测量的太阳视面中心拟合算法和月球视面中心拟合算法，用于确定太阳质心位置。虽然观测仪器及基本观测量不同，但算法原理仍值得借鉴。
灰度质心法要求太阳图像均匀、对称，且受噪声的影响严重[18]，在处理退化的太阳图像时误差较大，诸多文献研究表明拟合法的精度要好于灰度质心法[8]。太阳敏感器的视场普遍较大，从几十度到180°不等[19]。大视场的太阳敏感器投影模型比较特殊，而且视场边缘的畸变较大，会造成成像形变。当太阳在视场边缘成像时，太阳图像不再是圆形，此时仍然采用圆拟合的方法提取图像质心显然不再合适。
本文首先研究太阳在超大视场太阳敏感器中的成像形状，提出图像平面内的椭圆拟合算法，在一定程度上解决了非圆形太阳图像质心提取的问题。然后提出球面圆拟合算法，在物方空间确定真实太阳的质心位置。最后采用实测数据，对圆、椭圆和球面圆拟合算法进行比较，结果表明在一定的观测条件下，两种新算法具有更高的质心提取精度。
2 太阳投影原理常用的超大视场镜头的投影模型主要有4种：等立体角投影、等距投影、体视投影和正交投影[20]。本文采用尼康公司生产的AF DX Fisheye-Nikkor鱼眼镜头(标称焦距为10.5 mm，视场为180°)，采用美国Apogee仪器公司生产的Alta U9000 CCD，二者组合构建了鱼眼相机，即太阳敏感器。该镜头采用等立体角投影模型，投影成像公式为
式中，f为焦距；θ为物方半视场角；R为像点至像主点的极距。取太阳的物方角半径为16′，太阳质心的方位角A=45°，半视场角θ=0~89°，模拟不同半视场角对应的太阳边缘点，不考虑畸变影响，按等距投影模型将太阳的边缘点投影到像平面。图 1给出了焦距f=10.5 mm时，不同半视场角处太阳边缘点的理想成像形状。
 |
| 图 1 等立体角投影下太阳的理想成像形状 Fig. 1 Sun’s perfect image shape under solid angle projection |
由图 1及等立体角投影公式可知，当半视场角θ=0时，太阳图像为正圆。此后，随着半视角的增大，太阳越来越接近视场的边缘，此时太阳逐渐演化了“椭圆形”图像。太阳的半视场角越大，太阳图像的“椭圆性”越明显。
事实上，太阳在视场边缘的成像并非理想的椭圆，只是近似椭圆。根据圆锥曲线的定义可知，当平面与圆锥面相切，且平面既不与圆锥的母线垂直也不与其平行时，平面与圆锥面的交线才为椭圆。因此，当且仅当镜头为小孔成像投影模型时，太阳边缘经过投影后才可能形成圆锥曲面，与像平面相交后形成标准的椭圆形成像。若相机的镜头采用小孔成像投影，当物方半视场角达到90°，即成像视场达到180°时，要求CCD的物理尺寸为无限大，因此小孔成像投影一般不用于超大视场成像。
考虑到太阳的角半径仅为16′，其上下边缘的角距差也只有32′，因此基本可以认为等立体角投影获取的视场边缘太阳图像为椭圆形。图 2、图 3分别为采用本文的鱼眼相机拍摄半视场角分别为70°和84°(即仰角20°和6°)太阳获得的图像，并采用Sobel+Zernike矩算法进行亚像素边缘检测。算法的基本思想是：首先采用Sobel算子对太阳图像进行像素级的边缘粗检测，然后对每一个像素级边缘点5×5或7×7邻域的像素灰度值与模板进行卷积运算得到Zernike矩，最后实现边缘的亚像素精确定位[8]。本文采用中科院沈阳自动化研究所高世一推导的7×7 Zernike矩模板系数[13]。两幅太阳图像的亚像素边缘检测效果如图 2所示，均类似于椭圆形。
 |
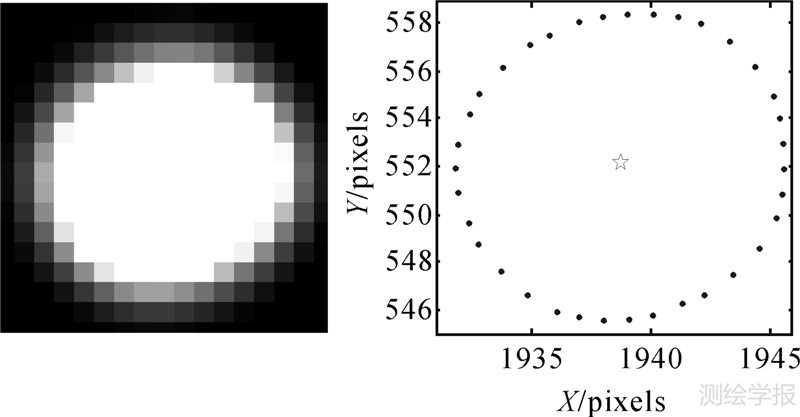| 图 2 太阳70°半视场角图像及其亚像素边缘检测结果 Fig. 2 A real image of the sun of 70° half angle of view and the result of subpixel edge detection |
 |
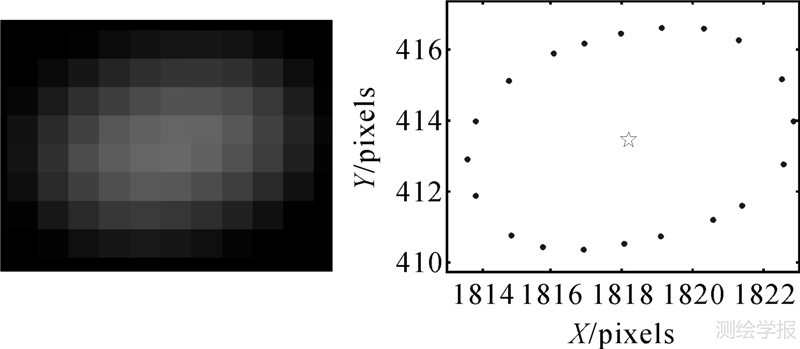| 图 3 太阳84°半视场角图像及其亚像素边缘检测结果 Fig. 3 A real image of the sun of 84° half angle of view and the result of subpixel edge detection |
从形状上来看，实际拍摄的太阳图像与模拟的太阳图像有一定的差别，原因可能是仿真计算没有考虑镜头畸变、成像色散等实际因素对太阳成像的影响。此外，镜头的制作加工也很难使成像为严格的等立体角投影模型。
事实上，根据不同投影的定义可知，只有在体视投影模型下，太阳的图像才为理想的正圆。在其他投影模型下，太阳的图像为近似椭圆。因此，采用圆拟合的算法提取太阳图像质心在理论上是不严密的。
3 像面椭圆拟合算法太阳在等立体角投影、等距投影和正交投影模型下的图像均为近似椭圆，因此可以尝试采用椭圆拟合的方法提取太阳图像的质心。设采用亚像素边缘检测算法得到太阳图像边缘点坐标序列为(x1,y1)、(x2,y2)、…、(xn,yn)，根据最小二乘法，在像平面拟合椭圆的误差方程为
式中，(xc,yc)为待估圆心坐标;a、b为待估的椭圆长、短半轴。
给定待估参数的近似值，对误差方程进行线性化，即可求解圆心坐标参数。根据残差序列估计圆心坐标的中误差mxc和myc，则圆心(即质心)位置中误差计算公式为
mc可作为衡量太阳图像质心提取的内符合精度指标。 4 球面圆拟合算法
由于太阳图像只是近似椭圆，直接在像平面采用椭圆拟合算法仍然不严密。受文献[16—17]的启发，本节将根据相机镜头的投影和畸变模型，将太阳图像的边缘点映射到物方空间，获取真实太阳边缘点的方位角和半视场角，并在物方空间进行球面圆拟合，确定太阳的质心位置。
如图 4所示，Z为相机的主光轴与天球的交点，Ek为真实太阳的某一边缘点在天球上的投影，C为真实太阳的质心在天球上的投影，它们构成了球面三角形。边缘点Ek的方位角和半视场角分别为Ak和θk，太阳质心C的方位角和半视场角分别为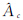
和
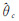，太阳的视半径为
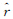。根据球面三角形边的余弦公式可得[21]
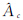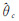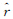,,)为未知参数，构建误差方程
 |
| 图 4 球面三角形 Fig. 4 Spherical triangle |
给定参数近似值X0=[Ac0θc0r0]T，对误差方程线性化
式中 假设有n个等精度的边缘点数据，则可构建n个误差方程，不妨令 根据最小二乘法可得 未知参数的估值为 单位权中误差μ及未知参数的权逆阵
表示为
故未知参数的精度估计公式为
实际计算中，上述过程需要迭代，一般只需2~3次迭代即可使结果收敛到0.1″以内。
根据投影模型，将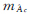
映射到像平面，即为质心位置的切向中误差
将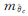
映射到像平面，即为质心位置的径向中误差
质心位置的中误差为
mc即为球面圆拟合算法的内符合精度指标。
下面总结给出采用球面圆拟合算法提取太阳图像质心的步骤：
(1) 采用Sobel+Zernike算法精确检测太阳图像的亚像素边缘坐标，其中Zernike矩的计算采用文献[13]提供的7×7模板。
(2) 根据相机的投影和畸变模型，将亚像素边缘点映射到物方空间，得到物方空间太阳边缘点在相机坐标系下的方位角和半视场角。其中相机参数采用恒星法检校技术获取，相机检校模型采用文献[20]提出的基于半视场角约束的等立体角投影多项式畸变模型。
(3) 采用球面圆拟合算法，拟合物方空间太阳质心的方位角和半视场角。
(4) 再次根据相机的投影和畸变模型，将物方空间太阳质心的方位角和半视场角映射到像平面，获取太阳图像质心坐标，并进行精度估计。
需要说明的是，在实际应用中，直接参与导航解算的观测量为物方空间太阳质心的方位角和半视场角，因此球面圆拟合算法并不需要进行第(4)步的计算，第(4)步的计算只是为了评价算法的精度。
从理论上讲，本节提出的球面圆拟合算法不再需要考虑太阳图像形状。无论太阳图像形状为圆、椭圆或者是近似椭圆，将其映射到物方空间后，其形状均为球面圆，球面圆拟合算法更为严谨。
5 算例分析2014-10-14在郑州地区利用本文的鱼眼相机对太阳进行长时间的跟踪观测，期间天气状况良好，相机全程保持静止不动，分两个时段进行：第1个时段观测起止时间(北京UTC)约为10:07—16:25，太阳的半视场角变化范围大约为42°~73.6°，设置较低的采样率获取了108幅太阳图像；第2个时段观测起止时间约为16:25—17:23，太阳的半视场角变化范围大约为73.6°~84°，设置较高的采样率获取了312幅太阳图像。因此，本次试验共获取了420幅太阳图像。试验中，相机拍摄太阳的极限半视场角只能达到84°，当太阳的半视场角进一步增大时，太阳接近于地平面，光照极弱，加之滤光片的减光作用，无法成像。
首先采用固定阈值对太阳图像进行分割，然后利用Sobel+Zernike矩算法检测太阳图像的亚像素边缘，最后分别采用以下3种算法提取太阳图像质心：①圆拟合算法；②椭圆拟合算法；③球面圆拟合算法。3种算法的质心位置中误差mc(即内符合精度)随半视场角的变化如图 5所示。
 |
| 图 5 质心位置中误差随半视场角的变化图 Fig. 5 Mean square errors of the centroids varies with the half angle of view |
图 5显示出两个重要的交叉点，分别大约发生在半视场角70°和80.3°。当太阳的半视场角小于70°时，3种算法的平均内符合精度分别为0.042 pixels、0.043 pixels和0.171 pixels，椭圆拟合算法的内符合精度略优于圆拟合算法，球面圆拟合算法的精度最差。随着半视场角的增大，椭圆拟合算法和圆拟合算法的内符合精度比较稳定，而球面圆拟合算法的内符合精度不断衰减。
当太阳的半视场角大于70°时，圆拟合算法和椭圆拟合算法的内符合精度迅速衰减，而球面圆拟合算法的内符合精度开始不断提高。椭圆拟合算法的内符合精度总是优于圆拟合算法，而且半视场角越大，这种优势越明显。椭圆拟合算法与球面圆拟合算法存在一个交叉点，大约发生在半视场角80.3°。当半视场角小于80.3°时，椭圆拟合算法的内符合精度要明显优于球面圆拟合算法；当半视场角大于80.3°时，球面圆拟合算法的内符合精度要明显优于椭圆拟合算法。由此可以说明，球面圆拟合算法更适合处理半视场角大于80.3°的太阳图像，而椭圆拟合算法更适合处理半视场角70°~80.3°的太阳图像。
将数据分为3段，第1段为半视场角小于70°的太阳图像，共计99张；第2段为半视场角大于70°小于80.3°的太阳图像，共计201张；第3段为半视场角大于80.3°的太阳图像，共计120张。采用16次多项式对3种算法的3段太阳图像质心轨迹分别进行拟合，拟合轨迹均平滑，统计残差的标准差进一步评价3种算法的精度，结果如表 1所示。
| 像素 | ||||
| 图幅号 | 半视场角 | 圆拟合算法 | 椭圆 拟合算法 | 球面圆 拟合算法 |
| 1—99 | 42°~70° | 0.055 | 0.055 | 0.065 |
| 100—300 | 70°~80.3° | 0.021 | 0.018 | 0.027 |
| 301—420 | 80.3°~84° | 0.034 | 0.027 | 0.022 |
由表 1可知，当太阳的半视场角为42°~70°时，圆和椭圆拟合算法要明显好于球面圆拟合算法；当太阳的半视场角为70°~80.3°时，椭圆拟合算法要好于圆和球面圆拟合算法；当太阳的半视场角为80.3°~84°时，球面圆拟合算法要好于圆和椭圆拟合算法。考虑到半视场角越小，太阳的圆形性越强，因此对于半视场角小于42°的太阳图像，建议采用圆拟合算法即可。此外，半视场角大于70°的太阳图像与半视场角小于70°的太阳图像相比，具有更好的拟合精度。分析原因，可能是因为后320幅图像跟踪观测时长仅为1 h，而前100幅图像的跟踪观测时长达到6 h。跟踪观测时间越长，太阳图像质心轨迹越长，多项式模型越难逼近其轨迹，导致拟合后的残差越大。
图 5出现80.3°这一拐点，可能是由畸变模型误差和太阳图像的椭圆性两个因素共同决定的。其中畸变模型误差是指所采用的畸变参数及模型不能准确描述真是畸变情况所产生的误差。当太阳的半视场角小于80.3°时，由于畸变较小，此时太阳图像的椭圆性较好，直接采用椭圆拟合算法精度较好。此时若采用球面圆拟合算法，不可避免地会引入畸变模型误差，进而影响球面圆拟合算法的精度。当太阳的半视场角大于80.3°时，畸变增大到一定程度后，太阳图像的椭圆性变差，从而影响椭圆拟合算法精度。此时采用球面圆拟合算法虽然会引入畸变模型误差，但大部分畸变已得到有效校正，因此球面圆拟合算法精度更好。
此外，本文在Matlab2010环境下统计了420张太阳图像质心提取耗费的时间。其中亚像素边缘检测总共耗时大约93.3 s，单幅太阳图像平均耗时0.222 1 s。圆拟合算法运算总时间为0.136 4 s，单幅太阳图像平均耗时0.328 ms；椭圆拟合算法运算总时间为0.144 6 s，单幅太阳图像平均耗时0.348 ms；球面圆圆拟合算法运算总时间为0.219 6 s，单幅太阳图像平均耗时0.528 ms。球面圆拟合算法的运算时间分别为圆和椭圆拟合算法的1.6倍和1.5倍。太阳图像质心提取的绝大部分的耗费在亚像素边缘检测上，占总时间的99.7%。考虑到球面圆拟合算法对单幅太阳图像的运算时间小于1 ms，因此，在权衡算法的精度和时间的关系时，基本可以忽略球面圆拟合算法的复杂性。
6 结 论根据实测数据的计算和分析结果，可以总结出3种太阳图像质心提取算法的适用范围：当太阳的半视场角小于70°时，建议采用圆拟合算法；当太阳的半视场角介于70°和80.3°时，建议采用椭圆拟合算法；当太阳的半视场角大于80.3°时，建议采用球面圆拟合算法。需要说明的是，上述结论只适用于本文采用的等立体角投影模型的鱼眼相机。对于其他不同种类的鱼眼相机，由于投影、畸变、成像色散等因素不同，可能会有不同的结论，但本文提供的分析方法是通用的。
在摄影测量领域，圆形目标的图像质心提取是经常遇到的问题。例如，近景摄影测量中经常采用的回光标志，航空摄影测量中的油罐、粮仓等均为圆形目标，本文提出的算法均可能适用。
| [1] | TREBI-OLLENNU A, HUNTSBERGER T, CHENG Y, et al. Design and Analysis of a Sun Sensor for Planetary Rover Absolute Heading Detection[J]. IEEE Transactions on Robotics and Automation, 2002, 17(6): 939-947. |
| [2] | D'AMARIO L A. Mars Exploration Rovers Navigation Results[J]. The Journal of the Astronautical Sciences, 2006, 54(2): 129-173. |
| [3] | FURGALE P, ENRIGHT J, BARFOOT T. Sun Sensor Navigation for Planetary Rovers: Theory and Field Testing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1631-1647. |
| [4] | JIA Chuanliang. Research on Digital Sun Sensor[D]. Harbin: Harbin Institute of Technology, 2007. (贾传良. 数字式太阳敏感器研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.) |
| [5] | ZHAN Y H, ZHENG Y, ZHANG C. Celestial Positioning with CCD Observing the Sun[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin: Springer, 2013: 697-706. |
| [6] | KROTKOV E, HEBERT M, BUFFA M, et al. Stereo Driving and Position Estimation for Autonomous Planetary Rovers[C]//Proceedings of IARP Workshop on Robotics in Space. Montreal, Canada: [s.n.], 1994. |
| [7] | LI Jianguo. Technical Research on Lunar Rover Position and Attitude Determination[D]. Beijing: Beijing University of Technology, 2007. (李建国. 月球车位姿确定技术研究[D]. 北京: 北京工业大学, 2007.) |
| [8] | YANG Peng, XIE Li, LIU Jilin. Zernike Moment Based High-accuracy Sun Image Centroid Algorithm[J]. Journal of Astronautics, 2011, 32(9): 1963-1970. (杨鹏, 谢立, 刘济林. 基于Zernike矩的高精度太阳图像质心提取算法[J]. 宇航学报, 2011, 32(9): 1963-1970.) |
| [9] | CHEN Xiaowei, XU Zhaohui, GUO Haitao, et al. Universal Sub-pixel Edge Detection Algorithm Based on Extremal Gradient[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 500-507. (陈小卫, 徐朝辉, 郭海涛, 等. 利用极值梯度的通用亚像素边缘检测方法[J]. 测绘学报, 2014, 43(5): 500-507.) |
| [10] | HERMOSILLA T, BERMEJO E, BALAGUER A, et al. Non-linear Fourth-order Image Interpolation for Subpixel Edge Detection and Localization[J]. Image and Vision Computing, 2008, 26(9): 1240-1248. |
| [11] | LI Zhe, DING Zhenliang, YUAN Feng. Subpixel Algorithm Based on Level Interpolation and Least Squares Fitting[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2008, 32(5): 615-618. (李喆, 丁振良, 袁峰. 基于分层插值和最小二乘拟合的亚像素细分算法[J]. 南京理工大学学报: 自然科学版, 2008, 32(5): 615-618.) |
| [12] | WU Guiping, XIAO Pengfeng, FENG Xuezhi, et al. A Method of Edge Feature Detection from High-resolution Remote Sensing Images Based on Frequency Spectrum Zone Energy[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 587-591. (吴桂平, 肖鹏峰, 冯学智, 等. 一种基于频谱段能量的高分辨率遥感图像边缘特征检测方法[J]. 测绘学报, 2011, 40(5): 587-591.) |
| [13] | GAO Shiyi, ZHAO Mingyang, ZHANG Lei, et al. Improved Algorithm about Subpixel Edge Detection of Image Based on Zernike Orthogonal Moments[J]. Acta Automatica Sinica, 2008, 34(9): 1163-1168. (高世一, 赵明扬, 张雷, 等. 基于Zernike正交矩的图像亚像素边缘检测算法改进[J]. 自动化学报, 2008, 34(9): 1163-1168.) |
| [14] | BIN T J, LEI A, CUI J W, et al. Subpixel Edge Location Based on Orthogonal Fourier-Mellin Moments[J]. Image and Vision Computing, 2008, 26(4): 563-569. |
| [15] | ZHANG K, CHEN H Q, LIANG Q W, et al. Subpixel Edge Detection Algorithm Based on Pseudo-Zernike Moments[C]//Proceedings of the International Society for Optical Engineering. Dalian, China: SPIE, 2010. |
| [16] | ZHAN Yinhu, ZHANG Chao, TANG Jiaxiang. A New Method of Fast Orientation by Surveying the Sun[J]. Geomatics Technology and Equipment, 2012, 14(2): 3-6. (詹银虎, 张超, 唐家祥. 一种新的测日快速定向方法[J]. 测绘技术装备, 2012, 14(2): 3-6.) |
| [17] | ZHAN Yinhu, ZHANG Chao, ZHENG Yong, et al. A Fitting Algorithm of the Apparent Moon Center and Its' Application on Fast Orientation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 353-358. (詹银虎, 张超, 郑勇, 等. 月球视面中心拟合算法及其在测月快速定向中的应用[J]. 测绘学报, 2012, 41(3): 353-358.) |
| [18] | ARES J, ARINES J. Influence of Thresholding on Centroid Statistics: Full Analytical Description[J]. Applied Optics, 2004, 43(31): 5796-5805. |
| [19] | HE Li, HU Yihua. Principium and Technology Development Tendency of Sun Sensors[J]. Electronic Components & Materials, 2006, 25(9): 5-7. (何丽, 胡以华. 太阳敏感器的原理与技术发展趋势[J]. 电子元件与材料, 2006, 25(9): 5-7.) |
| [20] | YUAN Yulei. Research on Fish-eye Camera Stellar Calibration Technology[D]. Zhengzhou: Information Engineering University, 2012. (原玉磊. 鱼眼相机恒星法检校技术研究[D]. 郑州: 信息工程大学, 2012.) |
| [21] | YU Feng, XIONG Zhi, QU Qiang. Multiple Circle Intersection-based Celestial Positioning and Integrated Navigation Algorithm[J]. Journal of Astronautics, 2011, 32(1): 88-92. (郁丰, 熊智, 屈蔷. 基于多圆交汇的天文定位与组合导航方法[J]. 宇航学报, 2011, 32(1): 88-92.) |