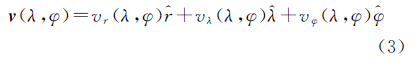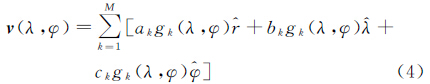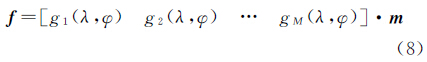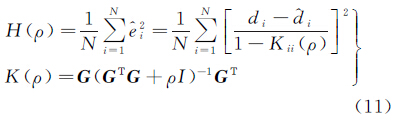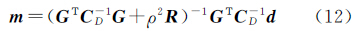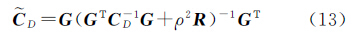2. 中国测绘科学研究院,北京 100830;
3. 深圳市勘察测绘院有限公司,广东 深圳 518028;
4. 国家基础地理信息中心,北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. Shenzhen Geotechnical Investigation and Surveying Institute Co.Ltd., Shenzhen 518028, China;
4. National Geomatics Center of China, Beijing 100830, China
1 引 言
2000国家大地坐标系(China Geodetic Coordinate System 2000,CGCS2000)于2008年7月1日开始作为我国法定的大地坐标系,CGCS2000采用ITRF97框架,2000.0历元[1, 2, 3]。在使用时,不同历元下的坐标转换到CGCS2000坐标系,需要进行框架和历元的转换,而历元转换则需要速度场模型。
GNSS、VLBI、DORIS和SLR等空间大地测量技术的发展极大地推动了速度场和板块运动的研究[3, 4, 5],中国地壳运动观测网络工程(简称“网络工程”)为研究中国大陆地壳运动速度场提供了丰富的数据[6]。速度场研究方面,文献[7]采用欧拉矢量法研究了中国大陆速度场,并给出了相关结果;文献[8]采用基于欧拉矢量的自适应拟合推估模型对中国大陆速度场进行解算,该方法可以顾及位移场的整体变化趋势和局部运动特征,提高水平运动速度场的计算精度;还有多面函数拟合法等方法[9, 10, 11],但是这些方法都不能对速度信号进行多尺度分析。
小波分析是目前多尺度分析的主要方法,球面小波分析技术把小波理论从无限空间的应用转移到球面有限空间。球面小波具有空间和频率局部化的能力,大尺度主要体现信号的低频信息,而小尺度对信号的局部特征更敏锐,主要体现信号的高频信息[12]。目前球面小波分析方法已经在重力场、磁场和温度场等领域中得到了运用[12, 13, 14]。文献[15]采用球面小波分析方法,利用GPS观测数据对美国南加利福尼亚州速度场进行了研究。
本文介绍了DOG(difference of Gauss)球面小波函数的性质[16],并利用“网络工程”的GPS观测数据,采用球面小波分析方法对中国大陆水平方向速度场进行了建模分析。
2 速度场的球面小波模型速度场球面小波模型的构建可简化为3个部分:①进行球面剖分,获得在球面近似均匀分布的离散格点,结合观测站点的位置,对离散格点进行取舍,选择球面小波函数,得到小波框架;②用小波框架表示站点速度;③求解模型待定系数,进行多尺度分析。
2.1 DOG球面小波DOG球面小波的函数表达式[16]为
式中,X为球面小波的中心极,且X∈S(球面);γ为中心极X(λ,φ)和球面上点X′(λ′,φ′)之间的夹角;(λ,φ)和(λ′,φ′)为点的经纬度;a=2-q,q为尺度,q=0,1,2,…;α>1,用于调节函数形状;λξ是以ξ、γ为变量的函数。图 1显示了以北极为中心极,q=3时,不同α所对应的球面小波函数图形,图 2显示了它们沿子午线的剖面。由图 1、图 2可以看出,球面小波函数的幅值随α、q的增大而增大;函数的空间支撑(以函数中心极为中心,函数ψX,a(X′)=0的最小解γ为半径的内部区域)随α的增大而增大,随q的增大而减小[15]。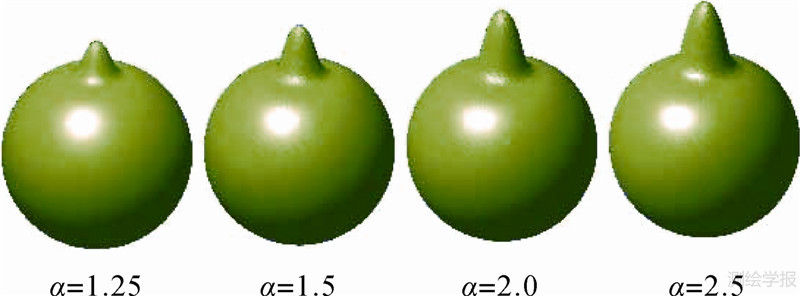 |
| 图 1 尺度相同(q=3)时不同α对应的球面小波 Fig. 1 DOG spherical wavelets centered at the north pole with q=3 and different α |
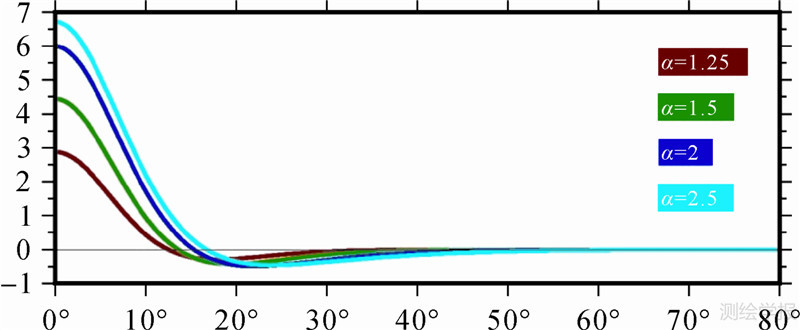 |
| 图 2 尺度相同(q=3)时不同α的球面小波函数沿子午线变化 Fig. 2 Different spherical wavelets’ changes along the meridian while q=3 |
 |
| 图 3 α=1.25时不同尺度球面小波函数的球谐系数 Fig. 3 Corresponding spectra of wavelets in different qwhile α=1.25 |
球面小波框架由一系列球面小波函数组成,函数之间可以是线性相关的,相对于基而言,它在表示信号时更加灵活,小波框架可通过对位置和尺度进行离散化得到[12]。通过对正二十面体进行球面三角剖分,可以获得在球面上近似均匀分布的球面三角格网[12, 18],剖分的层次和球面小波函数的尺度相对应,如图 4所示,不同的q对应于不同的尺度。
 |
| 图 4 正二十面体不同尺度的三角剖分 Fig. 4 Spherical triangle subdivision based on icosahedron |
将q=0,1,2,…,qmax球面剖分得到的格网点作为中心极,并定义不同尺度的球面小波函数,构成球面小波框架F
式中,X(q,j)为球面小波中心极;q为尺度;j为格点序号;Gq为球面格点的集合;a=2-q;X′含义同前。球面格点数随剖分层次呈指数增长,这将影响计算速度,因此对框架F的简化显得尤为重要。根据站点分布来选取框架可以减少框架中函数的数目,使模型变得更加实用[15]。简化过程如下:
(1) 去除“空间支撑”内部少于3个站点的框架函数,获得模型可用的最小尺度qmax;对于区域内任一点,若q对应的空间支撑内多于3个站点,则认为该点可用q尺度。
(2) 根据站点分布区域范围,求取“半径”L,L=2S/π,其中S为站点分布区域的球面面积(根据站点的最大、最小经纬度确定球面上4个点,将这4个点围成的区域按2个球面三角形的面积计算得到),根据L确定可用的最大尺度qmin,使得该尺度所对应的球面小波的空间支撑小于2L。
按该简化方法,站点分布范围越大qmin越小,站点密度越大则qmax越大。
2.3 球面小波表示站点速度的方法观测站点的速度可用沿东、北及垂直3个方向的速度来表示,站点(λ,φ)的速度v(λ,φ)表示为
式中,&rcirc;为垂直方向;&λcirc;为东方向;&φcirc;为北方向。由式(2)所得F作为估计速度场的框架,将速度场用小波函数表示为
式中,M为框架函数个数;gk(λ,φ)为第k个小波函数;ak、bk和ck分别为3个不同方向上的待定系数。对于给定的N个观测站点(λi,φi)(i=1,2,…,N),观测方程可写为 式中,nri、nλi和nφi为噪声。将观测方程(5)写为如下的矩阵形式
式中,f=[f1f2…fN]T;fi=[vrivλivφi]T;n=[nrinλinφi]为噪声;m为ak、bk和ck组成的模型向量,其求解方法详见2.4节。G的展开式为 式中,(λi,φi)为观测站点坐标;N为观测站点个数;M为框架函数个数。求得m后,区域内任一站点(λ,φ)的速度可由式(8)计算
均方根误差计算公式为
式中,Vi、&Vcirc;i分别为站点的模型值和观测值;t为点数量。 2.4 正则化问题与模型向量的求解通过离散化球面小波函数的位置和尺度的方式获取的小波框架可能存在冗余,采用该框架表示速度场将导致不唯一的解,另外观测误差以及数据分布不规则,将产生病态问题[13, 16]。对于速度场的球面小波模型,通过正则化方法[19],可以求解模型向量m,公式为
式中,d为已知站点上的速度值;CD为观测值的方差阵;Rkk′为正则化矩阵元素;S表示球面;ρ为正则化参数。正则化的目的是克服模型中线性方程组存在的病态问题,也有助于解决框架内球面小波函数之间不完全正交的问题[15]。正则化参数ρ采用交叉验证法(ordinary cross-validation,OCV,又称“留一交叉验证法”)求解[20, 21, 22, 23],首先去除一个观测点的数据,计算待求参数,然后计算该点的观测值与模型估值之差êi,继而选出最优的正则化参数。
OCV方法选择正则化参数的函数式可以表示为[15]
式中,di为第i个站点的观测值;&dcirc;i为模型使用所有观测数据时第i个站点对应的估值。当H(ρ)取最小值时,对应的ρ为选定的正则化参数。模型向量m的解可表示为
后验协方差计算公式[24]为
3 中国大陆GPS站点的球面小波分析采用“网络工程”跨度长达10年(1999—2009年)的GPS观测数据,其中包括基准网站点34个,基本网站点56个和区域网站点,共1068个。采用GAMIT/GLOBK(V10.35)软件,获得站点在ITRF2005框架下的东方向和北方向的速度值VE、VN。速度场在东、北和垂直3个方向的建模方法是一致的,由于垂直方向速度解算精度较差,只对东方向和北方向进行分析。
中国大陆GPS速度场的旋转趋势性非常明显,通常将欧拉旋转量作为趋势项。文中对VE、VN采用全局欧拉矢量法求解欧拉向量[6],得到旋转速率为0.28°/Ma,欧拉极为(43.27°N,87.31°W)。将VE、VN与采用全局欧拉矢量法获得的速度值之差称为剩余速度场V′E、V′N,作为球面小波模型建模数据,欧拉旋转速度作为速度场的趋势项。
选定站点的分布区域范围为(73°E—135°E,17°N—55°N),采用DOG球面小波,参数α=1.25,按框架简化方法,求出其球面面积,得到区域半径L约为5400km。当q=0时,其空间支撑为9167km<2L=10800km,可取qmin=0。当q=10尺度,球面小波空间支撑内至少包含3个站点的格点数为0,因此可取qmax=9,qmax的分布如图 5所示。
 |
| 图 5 区域内可用qmax分布 Fig. 5 Distribution of maximum q |
鉴于速度场趋势项已采用全局欧拉矢量法分离,取最大尺度qmin=2。因为可用小尺度q=8、9的区域极少,取模型最小尺度qmax=7,即算例中使用的模型尺度q为=2~7。需要说明的是,2.2节中框架函数选择方法只能初步选出适用尺度范围,更合适的建模尺度可根据qmax的分布及建模数据的实际情况做相应的调整。经计算共包括2050个框架函数,此时模型构建的方程组存在病态问题和秩亏问题。通过选择合适的正则化矩阵,将秩亏问题转化为满秩问题,获得稳定的解。
建模时首先采用模型对数据预处理,求取站点残差,并剔除站点残差大于3倍中误差的站点17个。采用剩下的站点数据作为建模数据,按式(11),求出V′E、V′N的正则化参数均为492,正则化参数的变化如图 6所示。
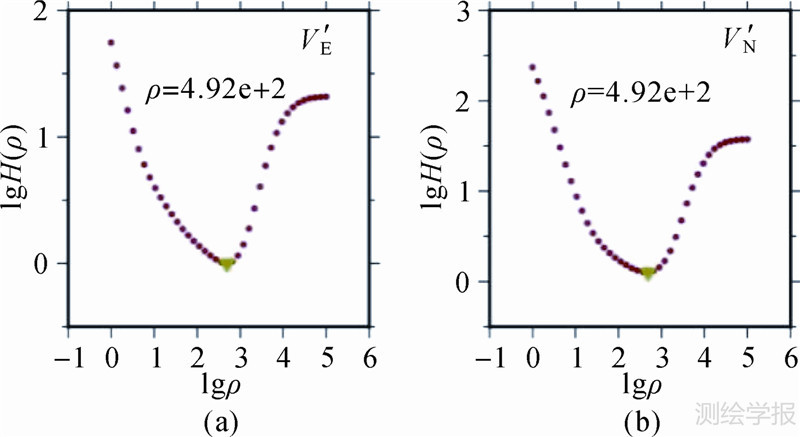 |
| 图 6 正则化参数 Fig. 6 Selection of regularization parameter |
按式(12)分别计算出V′E、V′NN的模型向量,按式(8)可估算站点的模型速度。模型中大尺度主要表征速度场的主要信息,小尺度主要刻画细节信息。随着大尺度与更多小尺度组合,模型对速度场体现出不断逼近的过程。当模型尺度q=2~7时,建模站点东方向、北方向的估计均方差分别为0.55mm/a、0.71mm/a。
按式(8)对速度场进行等间距格网内插,得到内插值在各个尺度的分量如图 7和图 8所示。图 7(a)、(b)为速度场模型在尺度q=2~5的分量,表示的是速度场的大尺度特征;图 7(c)、(d)为速度场模型值,即速度场的大尺度分量与局部细节特征之和。由图 7可以看出,中国大陆西南地区的相对运动较其他地区更大,大陆北部和南部分别存在向西和向东的相对性运动,大陆西部及东北部存在向北的运动,南部及西南部分地区存在向南的相对性运动特征。
 |
| 图 7 剩余速度场的球面小波模型多尺度估计 Fig. 7 The large-scale features of the residual velocity field |
 |
| 图 8 剩余速度场的细节特征 Fig. 8 The detail features of the residual velocity field |
速度场的小尺度分析必须要有足够密度的站点才能进行。图 8(a)、(b)和(c)、(d)分别表示模型在尺度q=6和q=7的分量,是速度场的细节特征。结合图 5,尺度q=6和q=7只有在部分区域可用,所以图 8(a)—(d)中只有在尺度q=6和q=7可用区域才有意义。从图 8中可以看出,在尺度q=6,西部地区存在东西向的相对运动,西南地区存在南北向的相对运动,具有明显的运动特征;而在尺度q=7,除西南局部地区存在明显的南北向的相对运动特征,其他区域在该尺度的分量主要呈点状不规则分布,表明在该尺度上无明显的运动特征。速度场的变化与地学运动(地震、局部重力变化等)存在联系,进一步的解释有待作更多分析。
GPS速度场的估值为剩余速度场的球面小波模型值与欧拉旋转速度之和,如图 9所示。由图 9(a)可以看出,中国大陆存在整体的向东运动趋势,由图 9(b)可以看出,西部主要是沿北方向的运动,而中部和东部主要为沿南方向的运动。东方向速度平均值为28.3mm/a,局部最大值为50.7mm/a;北方向速度绝对值的平均值为9.0mm/a,局部最大值为25.9mm/a。
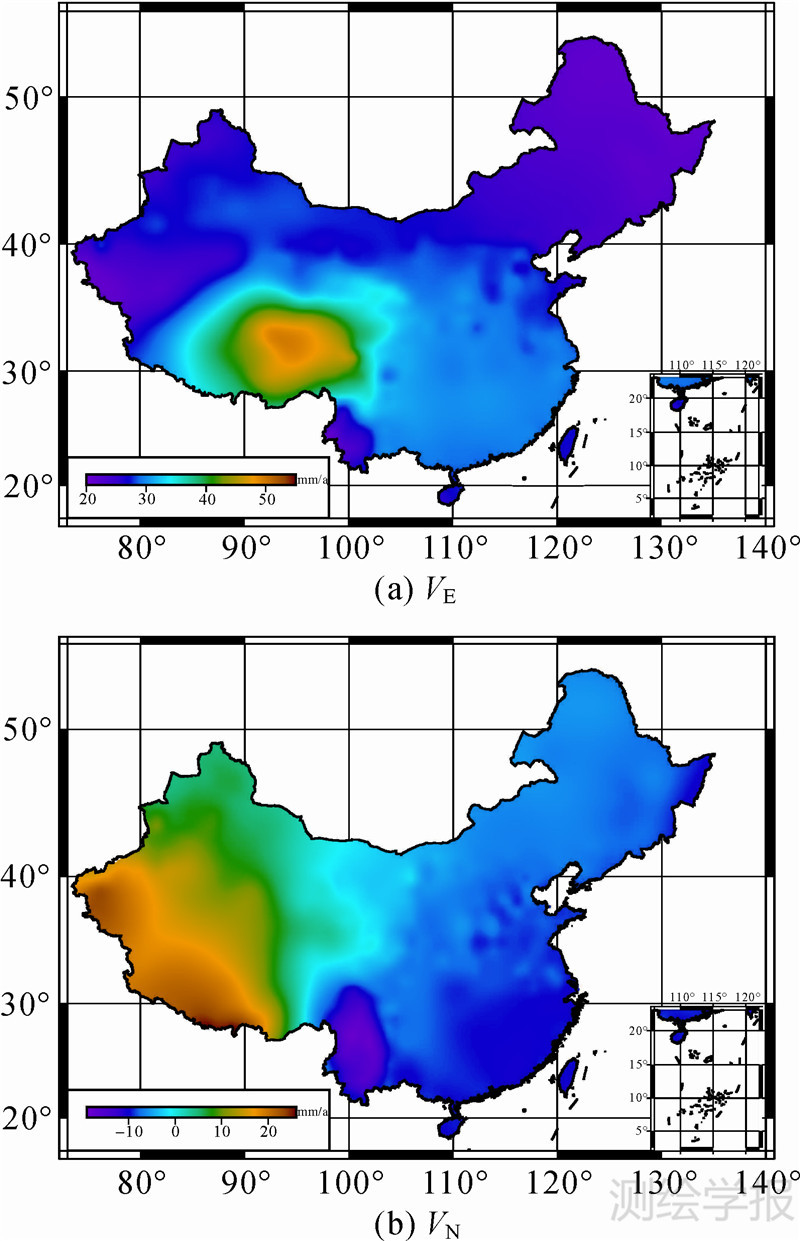 |
| 图 9 GPS速度场模型值 Fig. 9 The model value of GPS velocity fields |
为了检核模型的精度,在站点稠密和稀疏区域分别随机选取80个站点,将其从建模站点中剔除,作为模型外部检核点。测试站点如图 10(a)所示,红色为稠密区域外部检核站点,绿色为稀疏区域外部检核站点;图 10(b)为站点分布稠密处的外部检核误差;图 10(c)为站点分布稀疏处的外部检核误差。稠密和稀疏区域外部检核站点在东方向、北方向的估计均方差分别为±0.95mm/a、±0.97mm/a和±1.32mm/a、±1.30mm/a,两种方案外部检核统计结果见表 1。稠密区域的外部检核误差在-3~5mm/a,绝大部分在-1~1mm/a;稀疏区域外部检核误差波动相对较大,个别误差达到±10mm/a,这跟剔除站点时设置的阀值和站点分布有关。虽然剔除了部分粗差点,当外检核站点在数据稀疏的区域时(包括检核站点处于边沿区域),建模站点将更加稀疏,导致对模型缺乏足够的约束,出现个别外部检核误差较大的情况。这也说明使用时需要注意模型在站点稀疏区域(站点分布边沿)的精度较差的情况。
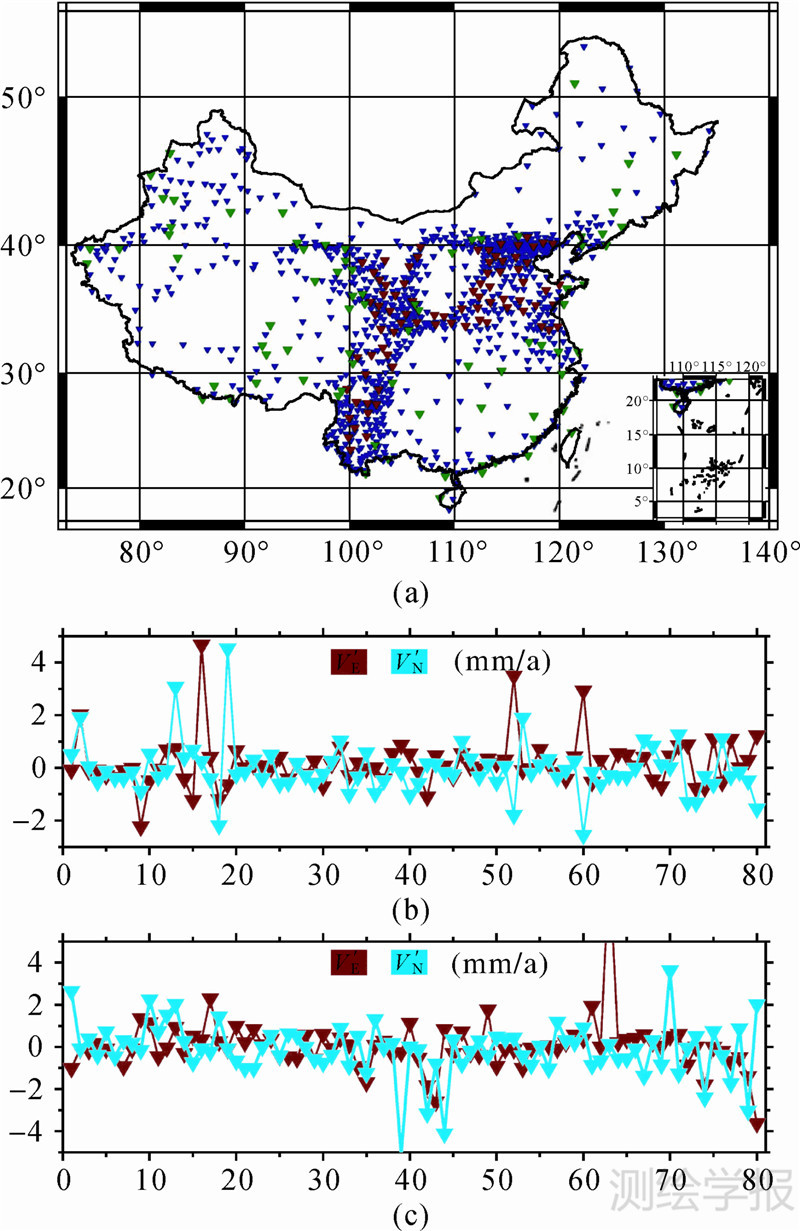 |
| 图 10 检核站点及其精度 Fig. 10 Distribution of stations and precision estimation |
采用全局欧拉矢量法只能顾及大陆的整体性运动趋势,不能反映局部范围的细节性运动。而多尺度估计方法对速度场具有很好的适用性,既可以刻画出大尺度特征,也可以表征小尺度运动。采用欧拉矢量法对速度场进行预处理,对剩余速度场采用球面小波模型,所获得的速度场模型精度较高。
| mm/a | |||||
| 方向 | 最大值 | 最小值 | 平均值 | 均方差 | |
| 稠密 | 东 | 4.67 | -2.23 | 0.19 | 0.95 |
| 区域 | 北 | 4.53 | -2.55 | -0.04 | 0.97 |
| 稀疏 | 东 | 8.68 | -3.62 | -0.06 | 1.32 |
| 区域 | 北 | 3.63 | -5.13 | 0.13 | 1.30 |
GPS速度场的球面小波模型按站点密度自适应确定可用的尺度,实现不同区域不同分辨率的分析。按框架简化方法,模型强调多个站点对速度场的共同作用,可以减小个别站点误差对模型精度的影响。
站点分布密度是影响多尺度分析的主要因素,对速度场模型的精度也有影响。另外,当计算范围大、已知站点较多时,将出现计算速度慢、占用内存大的情况,会对使用造成不便,此时区域分解算法可以有效地解决这类问题。
| [1] | CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS80 and WGS-84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 189-194. (程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS80和WGS-84的比较[J]. 测绘学报, 2009, 38(3): 189-194.) | http://www.cnki.com.cn/Article/CJFDTOTAL-CHXB200903000.htm
| [2] | CHENG Pengfei, CHENG Yingyan, WEN Hanjiang, et al. The User Guide of China Geodetic Coordinate System 2000[M]. Beijing: Surveying and Mapping Press, 2008. (程鹏飞, 成英燕, 文汉江, 等. 2000国家大地坐标系实用宝典[M]. 北京: 测绘出版社, 2008.) |
| [3] | CHENG Pengfei, CHENG Yingyan, BEI Jinzhong, et al. CGCS2000 Plate Motion Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 159-167. (程鹏飞, 程英燕, 秘金钟, 等. CGCS2000板块模型构建[J]. 测绘学报, 2013, 42(2): 159-167.) |
| [4] | LI Qiang, YOU Xinzhao, YANG Shaomin, et al. A Precise Velocity Field of Tectonic Deformation in China as Inferred from Intensive GPS Observations[J]. Science China: Earth Sciences, 2012, 55(5): 695-698. (李强, 游新兆, 杨少敏, 等. 中国大陆构造变形高精度大密度 GPS 监测——现今速度场[J]. 中国科学: 地球科学, 2012, 42(5): 629-632.) |
| [5] | CHENG Pengfei, WANG Hua, CHENG Yingyan, et al. The Trend of the APRGP Velocity Field and Plates Movement Derived from GPS Data[J]. Science China Physics, Mechanics & Astronomy, 2010, 53(4): 767-772. |
| [6] | NIU Zhijun, MA Zongjin, CHEN Xinlian, et al. Crustal Movement Observation Network of China[J]. Journal of Geodesy and Geodyanmics, 2002, 22(3): 88-93. (牛之俊, 马宗晋, 陈鑫连, 等. 中国地壳运动观测网络[J]. 大地测量与地球动力学, 2002, 22(3): 88-93.) |
| [7] | WEI Ziqing, LIU Guangming, WU Fumei. China Geodetic Coordinate System 2000: Velocity Field in Mainland China[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410. (魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系——中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410.) |
| [8] | YANG Yuanxi, ZENG Anmin, WU Fumei. Horizontal Crustal Movement in China Fitted by Adaptive Collocation with Embedded Euler Vector[J]. Science China: Earth Sciences, 2011, 54(12): 1822-1829. (杨元喜, 曾安敏, 吴富梅. 基于欧拉矢量的中国大陆地壳水平运动自适应拟合推估模型[J]. 中国科学: 地球科学, 2011, 41(8): 1116-1125.) |
| [9] | LIU Jingnan, YAO Yibin, SHI Chuang. Method for Establishing the Speed Field Model of Crustal Movement in China[J]. Geomatics and Information Science of Wuhan University, 2002, 27(4): 331-336. (刘经南, 姚宜斌, 施闯. 中国地壳运动整体速度场模型的建立方法研究[J]. 武汉大学学报: 信息科学版, 2002, 27(4): 331-336.) |
| [10] | JIANG Zhihao, ZHANG Peng, BEI Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471-476. (蒋志浩, 张鹏, 秘金钟, 等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J]. 测绘学报, 2009, 38(6): 471-476.) |
| [11] | WU Fumei, LIU Guangming, WEI Ziqing. Velocity Field Model of CGCS2000 Based on Euler Vector of Local Area[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 432-435. (吴富梅, 刘光明, 魏子卿. 利用局域欧拉矢量法建立CGCS2000速度场模型[J]. )武汉大学学报: 信息科学版, 2012, 37(4): 432-435. |
| [12] | CHAMBODUT A, PANET I, MANDEA M, et al. Wavelet Frames: An Alternative to Spherical Harmonic Representation of Potential Fields[J]. Geophysical Journal International, 2005, 163(3): 875-899. |
| [13] | PANET I, KUROISHI Y, HOLSCHNEIDER M. Wavelet Modelling of the Gravity Field by Domain Decomposition Methods: An Example over Japan[J]. Geophysical Journal International, 2011, 184(1): 203-219. |
| [14] | OH H S, KIM D. SpherWave: An R Package for Analyzing Scattered Spherical Data by Spherical Wavelets[J]. R News, 2007, 7(3): 2-7. |
| [15] | TAPE C, MUSé P, SIMONS M, et al. Multiscale Estimation of GPS Velocity Fields[J]. Geophysical Journal International, 2009, 179(2): 945-971. |
| [16] | BOGDANOVA I, VANDERGHEYNST P, ANTOINE J P, et al. Stereographic Wavelet Frames on the Sphere[J]. Applied and Computational Harmonic Analysis, 2005, 19(2): 223-252. |
| [17] | HEISKANEN W A, MORITZ H. Physical Geology[M]. LU Fukang, HU Guoli, Trans. Beijing: Surveying and Mapping Press, 1979. (海斯卡涅, 莫里斯. 物理大地测量学[M]. 卢福康, 胡国理, 译. 北京: 测绘出版社, 1979.) |
| [18] | ZHANG Shengmao, WU Jianping, ZHOU Kesong, et al. Spherical Triangle Subdivision and Analysis Based on Polyhedron[J]. Computer Engineering and Applications, 2008, 44(9): 16-19. (张胜茂, 吴健平, 周科松. 基于正多面体的球面三角剖分与分析[J]. 计算机工程与应用, 2008, 44(9): 16-19.) |
| [19] | HANSEN P C. Rank-deficient and Discrete Ill-posed Problems[M]. Philadephia: SIAM, 1998. |
| [20] | SHAO Jun. Linear Model Selection by Cross-validation[J]. Journal of the American Statistical Association,1993, 88(422): 486-494. |
| [21] | SHAO Jun. An Asymptotic Theory for Linear Model Selection[J]. Statistica Sinica,1997, 7(2): 221-264. |
| [22] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223. |
| [23] | WEISBERG S. Applied Linear Regression[M]. 5th ed. Hoboken: Wiley,2005. |
| [24] | TARANTOLA A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Philadephia: SIAM, 2005. |