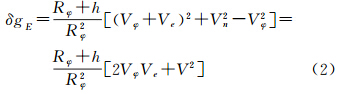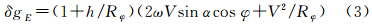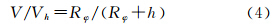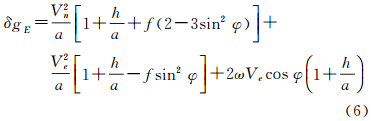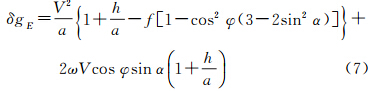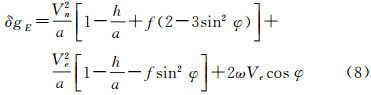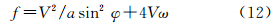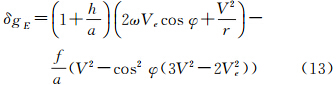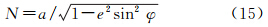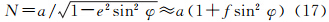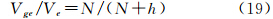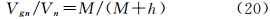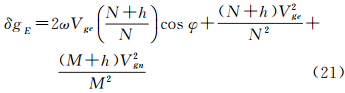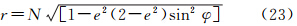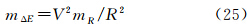2. 武汉大学测绘学院,湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
1 引 言
厄特弗斯(EÖtvÖs)改正是航空重力测量最重要的改正项之一。它是由于测量载体相对地球运动,使重力测量仪器受到附加的离心力作用而增加的一项改正,是车载、船载、机载等运动模式下的重力测量都必须顾及的共同改正项[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]。由于车载和船载测量速度较低,一般使用球近似公式计算厄特弗斯改正就能满足实用要求[4, 10]。因此,对于车载和船载重力测量,厄特弗斯改正计算公式在使用上并不存在异议。但在航空重力测量中,由于飞机速度可达300~500 km/h甚至更高,厄特弗斯改正计算公式的近似程度将直接影响到重力测量成果的质量,因此必须对此问题给予高度重视。由于历史上多种主客观的原因,在使用航空重力测量厄特弗斯改正公式问题上国内外至今仍未取得完全一致,近期出版的著作和发表的论文甚至作业标准仍在引用早期的近似公式[11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]。我国航空重力测量作业部门在使用厄特弗斯改正公式时也出现比较明显的引用错误,在一定程度上影响了航空重力测量成果的质量。针对此情况,本文全面分析比较了不同时期、不同形式厄特弗斯改正公式在数值上的差异,指出了我国目前使用近似公式存在的问题和统一使用严密公式的必要性,供实际作业部门参考。
2 不同形式厄特弗斯改正公式来源与分析 2.1 Thompson(1960)公式在运动载体上实施重力测量会产生厄特弗斯效应,最早是由匈牙利科学家EÖtvÖs于1919年发现并加以推证的。EÖtvÖs当年给出的球近似改正公式在船载重力测量中一直沿用至今,其公式形式为[4]
式中,δgE为厄特弗斯改正数;ω为地球自转角速度;V为载体运动速度;α为载体运动方位角;φ为测点大地纬度;R为地球平均半径。1958年以后,国际上陆续开展了航空重力测量试验,文献[5]最先推出针对航空重力测量的厄特弗斯改正公式,其形式为式中,Rφ为地球椭球在纬度φ处的向径;Vφ为由地球自转引起的地球表面上纬度φ处的切线速度;V为飞机速度在地球表面的投影;Ve为V的东向分量;Vn为V的北向分量;h代表飞机相对平均海面高度。将Vφ=Rφωcos φ和Ve=Vsinα代入式(2)得
不难看出,Thompson公式仍为球近似公式,与传统使用的海面船测重力改正公式(1)相比,其前面增加了乘系数(1+h/Rφ),它的意义相当于把飞机速度在地球表面上的投影值V转换为飞行高度上的速度。在Thompson公式发表后的一个时期内,国际上诸多文献都一致将该公式作为标准公式使用[6, 7, 8, 9]。我国早期的文献[1, 2, 19],包括近期出版的文献[20],也都一直引用该公式讨论航空重力测量数据归算问题。这里需要指出的是,Thompson公式中的V值代表的是飞机速度在地球表面的投影,即地面(或地表)速度(ground speed)[5],而不是通常理解的飞行高度上的速度Vh。我国相关引用文献几乎都忽略了以上两种速度之间的差异[1, 2, 19, 20],有的文献将地面速度理解为飞机相对地球的速度[2]。实际上,在球近似下,V和Vh之间存在如下简单的联系
按照原Thompson公式的推导思路,不难推出使用飞行高度上的速度Vh表示的另一形式的Thompson公式
由于飞行高度h相对Rφ是个很小的量,因此V和Vh之间的差异也不大,但在高精度测量要求中必须对它们加以区别。至于Thompson当年为什么要用地面速度而不直接用飞行高空速度,是由当时的测速技术条件所决定的,因为当时比较成熟的测速手段是地面摄影(ground photograph)和多普勒雷达(Doppler radar)技术[22],两种技术都能直接给出飞机的地面速度。
2.2 Harlan(1968)公式针对Thompson公式球近似可能带来不可忽视的误差影响,1968年,Harlan从几何学出发,推出了两组分别对应于地表速度和飞行高空速度、顾及地球椭球扁率的厄特弗斯改正公式[11],其形式为:
当V代表地表速度时,有
当V代表飞行高空速度时,有
式(6)-(9)中,a代表地球椭球长半轴;f为椭球扁率;其他符号意义同前。Harlan公式发表后,在国内外学术界得到了普遍认可并在实践中得到了广泛应用[3, 11, 12, 13, 14, 15, 16, 17, 18, 21]。但在这些大量的引用文献中,不乏有由于作者可能的疏忽而造成的引用错误。其中,文献[15]在引用时将式(7)右端第2项h/a前的“+”误写为“-”号;文献[16]引用的公式为
文中同时注明公式中的V值代表地表速度,且显然,式(10)存在多处错误:①右端第1项分母中的括号部分应该位于分子;②公式中的V值代表的应该是飞行高空速度;③f代表的应该是椭球扁率而不是式(11)所示的表达式。另外,文献[17]在引用式(9)时,也误将式中的f值理解为
令人更为遗憾的是,我国学者和作业规程在引用Harlan公式时也出现了理解上的偏差,文献[3]和文献[21]的引用公式为
显然,式(13)只是式(7)的简单变形体,两者应当是等价的,即式(13)中出现的地心向径r应该是a。上述两个文献之所以都把a写成r,可能是受到文献[11]中译本出现排版错误的误导[23]。另外,式(13)所对应的V值代表的应该是地表速度,而文献[3]和[21]都误将其标明为飞行高空速度。美国Micro-g LaCoste生产的TAGS型航空重力仪在数据处理软件中,也同样使用式(7)作为航空重力测量厄特弗斯改正计算模型[24],笔者经比对分析发现,软件中同样存在直接使用飞行高空速度替代地表速度的问题。上述引用错误不仅在理论上是不严密的,在实际应用中也会引起较大的数值偏差。因此,应当及时加以纠正。
2.3 严密计算公式由前面的分析得知,最早发表的Thompson公式只是一个球近似公式,后来发表的Harlan公式也只是一个顾及椭球扁率一阶项影响的近似公式。实际上,前面提及的一些重要文献在推演航空重力测量数学模型过程中,已经给出了厄特弗斯改正的严密计算公式[3, 14, 17, 25],其形式为
式中,V代表飞行高空速度;N和M分别代表地球椭球卯酉圈和子午圈曲率半径,其计算式分别为 式中,e为椭球第一偏心率,e2=2f-f2;其他符号含义同前。式(14)的具体推导过程见文献[3]。由式(14)知,当近似取N≈M≈R(即球近似)时,式(14)就转变为前面的Thompson公式,即式(5),如果近似取
将其代入式(14),作幂级数展开并取至椭球扁率一阶项,则不难得到以飞行高空速度表示的Harlan公式,即式(8)和式(9),其推导过程从略。
假如用Vg表示飞行高空速度V在地球表面的投影,Vge和Vgn分别表示Ve和Vn的投影,根据关系式
将其代入式(14),则可得到以地表速度表示的厄特弗斯改正严密计算式同样,如果将近似式(17)和式(18)代入式(21),则可得到以地表速度表示、顾及椭球扁率一阶项的Harlan公式,即式(6)和式(7)。
至此,笔者已经理清了Thompson公式、Harlan公式与严密计算公式之间的关系,同时给出了从严密公式推导Harlan公式的技术途径,其结果与Harlan从几何学角度出发推导结果是等价的[22]。但这里必须指出的是,前面所指的严密公式其实也只是相对地球视为旋转椭球而言的,即统一把椭球法线作为重力加速度的投影线处理。而实际上重力传感器感应的应该是重力加速度在重力垂线方向上的投影,法线和垂线的差异即垂线偏差对厄特弗斯改正的影响大小,取决于测量区域重力场的复杂程度。文献[22]认为,由于垂线偏差量值一般不超过30″,因此该项影响可以忽略不计。文献[26]则通过估算认为,当垂线偏差变化率超过1″/km时,该项影响可达几个mGal(1 mGal=1×10-5m/s2)甚至几十个mGal。由于篇幅所限,本文暂不涉及此问题的讨论。
在实际应用中,除了部分学者仍习惯于引用Harlan公式外,个别学者和机构在引用严密公式(14)时,往往又作了近似处理。文献[27]和[28]把N和M都近似取为地球平均半径R,即回归到简单的Thompson公式;文献[29]则是把(N+h)和(M+h)都近似取为地面计算点的地心向径r,即使用式(22)和式(23)
为了估算曲率半径近似误差对厄特弗斯改正计算结果的影响,取厄特弗斯改正球近似公式的第2项进行讨论
对上式求微分并写成中误差形式得
式中,mR代表球半径误差;mΔE代表由mR引起的厄特弗斯改正误差。取R=6371km;V=500km/h,可得到表 1的估算结果。
| mR/km | 1 | 5 | 10 | 15 | 20 | 30 |
| mΔE/mGal | 0.05 | 0.24 | 0.48 | 0.71 | 0.95 | 1.43 |
由表 1计算结果可以看出,在高精度测量要求条件下,大于5 km的曲率半径误差对厄特弗斯改正计算结果的影响都是不可忽略的。而由椭球大地测量学得知,从赤道到两极,卯酉圈曲率半径N的变化幅度接近22 km,子午圈曲率半径M的变化幅度达64 km,地球椭球平均半径R与N的互差范围为7~28 km,R与M的互差范围为-36~28 km。由此可见,任何对曲率半径作近似处理的做法都是不可取的。
3 不同形式厄特弗斯改正公式数值差异分析 3.1 模拟数值比对分析为了准确掌握不同形式厄特弗斯改正公式在数值上的差异大小,这里选择严密公式(14)作为基准,分别计算Thompson公式(3)和式(5)、Harlan公式(7)和式(9)、我国作业规范采用的公式(13)及俄罗斯生产设备GT-1A采用的公式(22)与基准值的差异。其中,为了说明引用错误可能带来的误差大小,各计算式中的V统一直接采用飞行高度上的速度,并取飞行高度h=3000 m,V=500 km/h;同时采用2000国家大地坐标系(CGCS2000)定义的地球椭球参数[30],即
a=6 378 137.0 m
R=6 371 008.771 4 m
f=1/298.257 222 101
ω=7.292 115×10-5rad/s
e2=0.006 694 380 022 90
不同纬度测点相对于不同航向角上的计算比对结果分列于表 2-表 4。
| mGal | ||||||||
| α/(°) | 0 | 45 | 90 | 135 | 180 | 225 | 270 | 315 |
| 式(14) | 304 | 1736 | 2328 | 1736 | 304 | -1129 | -1723 | -1129 |
| 式(14)-式(3) | 1.41 | -0.28 | -1.58 | -0.28 | 1.41 | 1.07 | 0.33 | 1.07 |
| 式(14)-式(5) | 1.70 | 0.68 | -0.34 | 0.68 | 1.70 | 0.68 | -0.34 | 0.68 |
| 式(14)-式(7) | -0.28 | -0.95 | -1.24 | -0.95 | -0.28 | 0.39 | 0.67 | 0.39 |
| 式(14)-式(9) | 0.01 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 |
| 式(14)-式(13) | -0.13 | -0.81 | -1.09 | -0.81 | -0.13 | 0.54 | 0.81 | 0.54 |
| 式(14)-式(22) | 1.89 | 0.88 | -0.14 | 0.88 | 1.89 | 0.88 | -0.14 | 0.88 |
| mGal | ||||||||
| α/(°) | 0 | 45 | 90 | 135 | 180 | 225 | 270 | 315 |
| 式(14) | 303 | 1315 | 1734 | 1314 | 303 | -710 | -1131 | -710 |
| 式(14)-式(3) | -0.11 | -1.10 | -1.80 | -1.10 | -0.11 | -0.14 | -0.45 | -0.14 |
| 式(14)-式(5) | 0.17 | -0.34 | -0.84 | -0.34 | 0.17 | -0.34 | -0.84 | -0.34 |
| 式(14)-式(7) | -0.28 | -0.76 | -0.96 | -0.76 | -0.28 | 0.19 | 0.39 | 0.19 |
| 式(14)-式(9) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 式(14)-式(13) | -0.64 | -1.12 | -1.32 | -1.12 | -0.64 | -0.17 | 0.03 | -0.17 |
| 式(14)-式(22) | -0.14 | -0.65 | -1.15 | -0.65 | -0.14 | -0.65 | -1.15 | -0.65 |
| mGal | ||||||||
| α/(°) | 0 | 45 | 90 | 135 | 180 | 225 | 270 | 315 |
| 式(14) | 301 | 326 | 337 | 326 | 301 | 276 | 266 | 276 |
| 式(14)-式(3) | -1.64 | -1.65 | -1.65 | -1.65 | -1.64 | -1.62 | -1.62 | -1.62 |
| 式(14)-式(5) | -1.35 | -1.35 | -1.35 | -1.35 | -1.35 | -1.35 | -1.35 | -1.35 |
| 式(14)-式(7) | -0.28 | -0.30 | -0.30 | -0.30 | -0.28 | -0.27 | -0.27 | -0.27 |
| 式(14)-式(9) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 式(14)-式(13) | -1.16 | -1.17 | -1.17 | -1.17 | -1.16 | -1.15 | -1.14 | -1.15 |
| 式(14)-式(22) | -2.17 | -2.17 | -2.17 | -2.17 | -2.17 | -2.17 | -2.17 | -2.17 |
由前面的分析得知,式(5)、式(9)和式(22)与严密公式(14)的差异主要源于曲率半径的近似处理。式(3)和式(5)、式(7)和式(9)原本是等价的,但在实际引用中,往往出现飞行高空速度和地表速度混淆使用的情况,由此引起了额外的误差。由表 2-表 4的计算结果可以看出,基于球近似的Thompson公式(3)和式(5),误差量值接近2 mGal;基于曲率半径顾及椭球扁率一阶项影响的Harlan公式(7)和式(9),误差量值不超过0.1 mGal,但当出现飞行高空速度和地表速度混淆使用时,其带来的计算误差可达1 mGal;式(13)没有严格区分飞行高空速度和地表速度,同时误用地心向径r代替地球椭球长半轴a,由此引起的计算误差超过1 mGal;式(22)忽略飞行高度同时对曲率半径作近似处理,其误差量值超过2 mGal。
对于区域性的航空重力测量,由于在单一测线上的飞行速度、航向和航高都基本保持稳定,测点纬度变化范围也相当有限。因此,以上由于各种原因引起的计算偏差一般都具有系统性误差特征,它们对测量成果质量的影响不可忽视。此外,目前国际上航空重力测量的精度已达1~3 mGal[14, 18, 27],如果不顾及以上计算偏差的影响,势必限制测量成果精度的进一步改善。因为在测量学科领域,通常要求理论模型的计算精度应该比仪器观测量精度高出1个数量级甚至更高。表 2-表 4的计算结果对应于飞行速度V=500 km/h,如果飞行速度降低到300 km/h甚至更小,则表中所列各类误差都将相应减小。
3.2 实测数据比对分析2012年,笔者所在单位在南海某海域开展了多种形式的航空重力测量飞行试验,其中包括使用多台套重力仪在东-西、南-北、西北-东南等特定方向上开展重复测线飞行试验。测线长度东-西向约240 km,南-北向约200 km,西北-东南向约350 km,测量期间飞行高度约1500 m,飞行速度约400 km/h。对重复测线试验数据进行分析比对后发现,所有同向飞行的重复测线观测数据内符合精度都很高,与仪器厂家标称的测量精度基本相符。但对向(或称正反向)飞行数据的比对情况有所不同,除南-北向外,东-西向和西北-东南向重复测线的对向观测数据比对结果都显示,两者之间存在比较明显的系统性偏差。经进一步分析研究后确认,除了某些环节上的测量环境效应改正还不够完善外,厄特弗斯改正公式使用不当也是造成出现上述现象的主要原因。为了突出说明后者的影响,这里单独列出两型仪器(美国公司生产的TAGS型和LCR Ⅱ型)分别使用Harlan公式(7)和我国作业规范公式(13),计算厄特弗斯改正的对向飞行数据比对结果(统一采用飞行高度上的速度)。其中,每一方向都给出3组计算结果,分别对应于正向和反向飞行使用近似厄特弗斯改正公式带来的误差统计,以及正向与反向互差带来的累积误差统计,具体见表 5和表 6。
| mGal | ||||||
| 测线方向 | 最大 | 最小 | 平均 | 均方根 | 测点数 | |
| 东-西 | 正向 | -0.502 | -0.521 | -0.510 | 0.510 | 1931 |
| 反向 | 0.291 | 0.287 | 0.289 | 0.289 | ||
| 互差 | -0.791 | -0.810 | -0.799 | 0.799 | ||
| 西北-东南 | 正向 | 0.212 | 0.197 | 0.206 | 0.206 | 2848 |
| 反向 | -0.376 | -0.444 | -0.393 | 0.393 | ||
| 互差 | 0.609 | 0.585 | 0.599 | 0.599 | ||
| 南-北 | 正向 | -0.072 | -0.082 | -0.077 | 0.077 | 1411 |
| 反向 | -0.099 | -0.112 | -0.105 | 0.105 | ||
| 互差 | 0.036 | 0.021 | 0.028 | 0.029 | ||
| mGal | ||||||
| 测线方向 | 最大 | 最小 | 平均 | 均方根 | 测点数 | |
| 东-西 | 正向 | -0.509 | -0.529 | -0.517 | 0.518 | 1931 |
| 反向 | 0.285 | 0.281 | 0.283 | 0.283 | ||
| 互差 | -0.792 | -0.812 | -0.801 | 0.801 | ||
| 西北-东南 | 正向 | 0.208 | 0.182 | 0.196 | 0.196 | 2848 |
| 反向 | -0.391 | -0.462 | -0.401 | 0.401 | ||
| 互差 | 0.607 | 0.585 | 0.597 | 0.597 | ||
| 南-北 | 正向 | -0.075 | -0.092 | -0.084 | 0.084 | 1411 |
| 反向 | -0.107 | -0.122 | -0.114 | 0.115 | ||
| 互差 | 0.038 | 0.023 | 0.030 | 0.030 | ||
从表 5和表 6的计算结果可以看出,尽管这里的试验飞行速度和高度相对于前面的模拟数据都有所降低,但无论是使用公式(7)还是公式(13),由于公式使用不当引起的系统性偏差仍达0.5 mGal,重复测线正反向互差最大可达0.8 mGal。显然,与仪器厂家标称的测量精度(优于1 mGal)相比较[24],以上误差影响量值大小都是不可忽略的。
由于南-北向测线正向与反向计算误差符号相同,同时量值较小,求互差时有相互抵消作用,因此在此方向上由公式使用不当引起的计算偏差几乎可以忽略不计。
文献[3]介绍了使用LCR Ⅰ型重力仪在我国山西大同地区的试验情况,其中测量飞行平均高度为3400 m,飞行速度为360 km/h。就该试验而言,如果使用公式(7)计算厄特弗斯改正数,那么东-西方向测线正向飞行的计算偏差为-0.76 mGal,反向飞行的计算偏差为0.43 mGal,重复测线互差值的计算偏差为-1.19 mGal;如果使用作业规范公式(13)进行计算,那么东-西方向测线正向飞行的计算偏差为-0.89 mGal,反向飞行的计算偏差为0.30 mGal,重复测线互差值的计算偏差为-1.19 mGal。以上误差量值比表 5和表 6的比对结果还要大一些。
4 结论与建议综合前面的分析、推演和比对结果可以看出:
(1) 尽管航空重力测量厄特弗斯改正的严密计算公式并不复杂,但国内外机构和学者在使用厄特弗斯改正公式问题上至今还缺乏统一。
(2) 与严密计算公式相比较,不同时期发表的不同形式的厄特弗斯改正公式都存在一定大小的系统性偏差。虽然Harlan(1968)公式逼近度较高,但经常出现使用不当的情况,由此引起的计算偏差不可忽略。
(3) 我国航空重力测量作业规范采用的厄特弗斯改正公式存在比较明显的引用错误,建议有关部门尽快对其进行更正,统一采用厄特弗斯改正严密计算公式。
| [1] | FANG Jun. Gravimetry and Figure of the Earth[M].Beijing: Science Press, 1965.(方俊.重力测量与地球形状学[M].北京:科学出版社,1965.) |
| [2] | GUAN Zelin, NING Jinsheng. Figure of the Earth and the External Gravitational Field [M]. Beijing: Surveying and Mapping Press,1981.(管泽霖,宁津生.地球形状及外部重力场[M].北京:测绘出版社,1981.) |
| [3] | SUN Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004.(孙中苗.航空重力测量理论、方法及应用研究[D].郑州:信息工程大学,2004.) |
| [4] | HUANG Motao, ZHAI Guojun, GUAN Zheng,et al.The Determination and Application of Marine Gravity Field[M]. Beijing: Surveying and Mapping Press,2005.(黄谟涛,翟国君,管铮,等. 海洋重力场测定及其应用[M]. 北京:测绘出版社,2005.) |
| [5] | THOMPSON L G D,LACOSTE L J B. Aerial Gravity Measurements[J]. Journal of Geophysical Research,1960,65 (1):305-322. |
| [6] | NETTLETON L L, LACOSTE L J B, HARRISON J C. Tests of an Airborne Gravity Meter[J]. Geophysics, 1960,25(1): 181-202. |
| [7] | NETTLETON L L, LACOSTE L J B, GLICKEN M. Quantitative Evaluation of Precision of Airborne Gravity Meter[J]. Journal of Geophysical Research, 1962,67(11): 4395-4410. |
| [8] | HARRISON J C. The Measurement of Gravity[J]. Proceedings of the IREE, 1962,50(11):2302-2312. |
| [9] | GLICKEN M. Eotvos Corrections for a Moving Gravity Meter[J]. Geophysics,1962,27(4):531-533. |
| [10] | DEHLINGER P. Marine Gravity [M].New York: Elservier Scientific Publishing Company, 1978. |
| [11] | TORGE W. Gravimetry[M].Berlin:Walter de Gruyter,1989. |
| [12] | BELL R E, BERNARD J C, ROBERT W S. Airborne Gravimetry from a Small Twin Engine Aircraft over the Long Island Sound[J]. Geophysics, 1991, 56(9):1486-1493. |
| [13] | FORSBERG R, OLESEN A V, KELLER K. Airborne Gravity Survey of the North Greenland Shelf 1998[M].Copenhagen:[s.n.], 1999. |
| [14] | OLESEN A V. Improved Airborne Scalar Gravimetry for Regional Gravity Field Mapping and Geoid Determination [D].Copenhagen: University of Copenhagen, 2003. |
| [15] | RIEDEL S. Airborne-based Geophysical Investigation in Dronning Maud Land, Antarctica[D]. Bremen:University Bremen,2008. |
| [16] | NEUMEYER J, SCHAFER U, KREMER J, et al. Derivation of Gravity Anomalies from Airborne Gravimeter and IMU Recording—Validation with Regional Analytic Models Using Ground and Satellite Gravity Data[J]. Journal of Geodynamics, 2009, 47:191-200. |
| [17] | ALBERTS B. Regional Gravity Field Modeling Using Airborne Gravimetry Data[C]//Publications on Geodesy 70, Netherlands Geodetic Commission. Delft:[s.n.],2009. |
| [18] | JEKELI C. Moving-Base Gravimetry[C]//Supplemental Notes to Gravimetic Geodesy, GS776.Columbus:[s.n.], 2012. |
| [19] | ZHANG Shanyan. On the Eötvös Problem for Aerial Gravity Measurement [J]. Acta Geodaetica et Geophysica, 1982,4:97-104.(张善言.航空重力测量的厄特弗斯问题[J].测量与地球物理集刊,1982,4:97-104.) |
| [20] | LÜ Zhiping, QIAO Shubo. Foundation of Geodesy[M]. Beijing: Surveying and Mapping Press,2010.(吕志平,乔书波.大地测量学基础[M].北京:测绘出版社,2010.) |
| [21] | Headquarters of General Equipment. GJB 6561-2008.Rules for Operations of Airborne Gravimetry[S]. Beijing: Military Standard Press of the Headquarters of General Equipment, 2008.(总装备部.GJB 6561-2008.航空重力测量作业规范[S].北京:总装备部军标出版发行部,2008.) |
| [22] | HARLAN R B. Eötvös Corrections for Airborne Gravimetry[J].Journal of Geophysical Research, 1968, 73(14):4675-4679. |
| [23] | TORGE W. Gravimetry[M]. Beijing: Earthquake Press, 1993.(TORGE W.重力测量学[M].北京:地震出版社,1993.) |
| [24] | LIANG Xinghui, LIU Lintao, WU Pengfei, et al. Study on CHZ Gravimeter Applied in Airborne Gravimetry Involving Error Spectrum Characteristic[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):633-639.(梁星辉,柳林涛,吴鹏飞,等. 顾及误差频谱特性的CHZ重力仪航空应用研究[J]. 测绘学报,2013,42(5):633-639.) |
| [25] | WALL R E. Airborne Gravimetry Erros Associated with Geoidal Undulations[J]. Journal Geophysical Research, 1971, 76(29):7293-7295. |
| [26] | HWANG C, HSIAO Y S, SHIH H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey: Data Reduction and Accuracy Assessment[J]. Journal Geophysical Research, 2007, 112(B10), doi: 10.1029/2005JB004220. |
| [27] | SHIH H C. Multiple-Altitude Airborne Gravity Surveys and Applications to Geoid Determination and Kuroshio Current[D]. Taiwan:National Chiao Tung University, 2010. |
| [28] | Joint-Stock Company.Gravimeter Training Abstract for Airborne Gravimeter Model GT-1A[C]//Proceedings of Scientific and Technological Enterprise. Moscow:[s.n.], 2008. |
| [29] | Headquarters of General Equipment. GJB 6304-2008.China Geodetic System 2000[S]. Beijing: Military Standard Press of the Headquarters of General Equipment, 2008.(总装备部.GJB 6304-2008.2000中国大地测量系统[S].北京:总装备部军标出版发行部,2008.) |