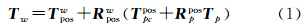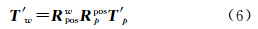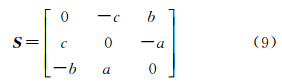2. 北京数字政通科技股份有限公司,北京 100082
2. Beijing eGova Company Limited, Beijing 100082, China
1 引 言
全景相机是一种用于拍摄空间360°×180°视场角的相机,能够无遗漏拍摄场景的全貌,从而获得对空间各个方向有沉浸感的全景影像。早在2004年,Google将全景相机应用于街景拍摄并于2007年推出地图街景。2005年,亚马逊旗下搜索引擎A9.com在本地搜索服务中提供街景查看功能。腾讯和百度分别于2011年和2013年先后推出SOSO地图街景服务和百度全景地图。随着移动测量技术的发展,全景相机逐渐被用来构建车载移动测图系统。移动测图系统[1]通常集成3类传感器,导航传感器(如GPS、IMU)、相机(如立体相机、全景相机)以及测距传感器(如2D/3D LiDAR)。标定是保证车载移动测图系统获取精确数据的重要前提,主要包括传感器部件自身的标定(又称内方位元素的标定)和传感器之间空间关系的配准(又称外方位元素的标定)[2]。传感器部件的自身标定一般由生产厂家在实验室内完成,这里不作讨论。传统立体相机(多采用CCD相机)外方位元素的标定,方法相对成熟。通常采用摄影测量方法[3],即首先在实际场景中建立高精度的已知控制点,然后直接在左右图像上确定控制点,应用空间交会方法解算相机外方位元素。与CCD相机相比,由于成像机理差异,全景相机是非量测相机,其成像是大于半球视场的球面成像,有别于传统的透视投影成像且360°大场景全是曲面镜反射得到,所得全景影像分辨率会有所下降且分布不均匀[4,5],传统可量测立体相机常采用摄影测量方法进行标定的方法已经不适合全景相机。
目前针对由全景相机和POS集成的车载移动测图系统外方位元素的标定研究相对较少,方法也不成熟。文献[6]提出基于标定板的标定方法,并将其应用于2D LiDAR和透视相机外方位元素的标定;文献[7, 8]相继发展了文献[6]的方法,分别将其应用于3D LiDAR和全景相机外方位元素标定以及内外方位元素的同时标定;文献[9, 10]在标定中不使用任何标定板,通过构建实际场景中线或面的相关性来进行标定。文献[11, 12]则采用不使用场景先验知识和标定板,仅仅利用多视图场景下点的相关来进行标定的自标定方法。文献[13, 14]提出利用实际场景中任意的3个相互正交或非正交面来进行全景相机和3D LiDAR外方位元素标定的方法。上述标定方法多是直接求解相机相对扫描仪的旋转和平移参数,试验的系统中没有集成POS,未利用绝对定位技术,而绝对定位技术是移动测量的核心[15]。为此,针对由全景相机和POS集成的车载移动测图系统,提出一种外方位元素标定的方法,即通过构建全景球面模型,将全景影像反投影到该球面上,从球面上选择控制点而不是直接在存在扭曲的全景影像上选择控制点,进而获得控制点在全景影像的球面坐标,建立点的相关性,从而求解出全景相机相对GPS/IMU的平移与旋转参数并进行实际场景精度验证。 2 车载全景相机Ladybug3结构
本文研究是基于北京数字政通科技股份有限公司研制的移动测图系统进行的,见图 1。系统由POS、3D LiDAR、全景相机(Ladybug3)、集成同步控制器以及工业计算机组成。POS主要包括惯性测量单元IMU和GPS,用于获取系统时间、系统平台位置和姿态;三维激光扫描仪用于获取目标地物的空间三维坐标数据;全景相机用于采集360°全景影像。本文的研究主要涉及该系统中由全景相机和POS集成的移动测图系统外方位元素的标定问题。系统中使用的POS由测量型的双频GPS、捷联惯导、旋转编码器式里程计这3种设备组合构成。组合方法是以捷联惯导和里程计推测定位为主,定期用差分GPS信息进行校正。系统中使用的全景相机为Ladybug3(见图 2),该全景相机由6台数字相机(采用鱼眼镜头)拼接组成,5台分布在侧面,1台在顶部,可覆盖整个全景360°球面图像的75%以上。软件包Ladybug Cap能够实时完成图像采集、处理、拼接和校正等工作,将多台相机采集的实景图像组合成一幅球面全景影像,其像元尺寸为4.4μm,有效视场角为360°×135°,镜头焦距为3.3mm,全景影像大小为5120像素×2560像素。
 |
| 图 1 移动测图系统 Fig. 1 Mobile mapping system |
 |
| 图 2 全景相机Ladybug3及拼接后全景影像 Fig. 2 Ladybug3 body and the merged 360°panoramic image |
基于全景相机和POS集成的车载移动测图系统,其外方位元素标定的目的是确定全景相机与POS之间的相对位置姿态关系。为了更好地描述标定方法,将标定中涉及的主要坐标系介绍如下。
(1) 全景球面模型坐标系(PC):Ladybug3的6个鱼眼相机在几何上共享一个投影中心[16],以该中心为坐标原点,半径为1m,X轴指向东,Y轴指向北,Z轴指向天。全景影像上的控制点反投影到该球面模型坐标系中,得到其球面坐标,参与标定运算。
(2) POS坐标系(POS):该坐标系由GPS天线位置和IMU的轴向来确定。原点位于GPS天线中心,X轴、Y轴和Z轴方向由IMU的3轴方向确定。
(3) 大地坐标系(W):采用WGS-84高斯-克吕格3°带投影坐标系。用于标定处理后的全景影像点坐标和全站仪测量的控制点坐标均在该坐标系表示。 3.1 基本原理
如图 3所示,对于任意全景影像上的点在全景球面模型坐标系中的坐标向量Tp,其对应地面控制点在大地坐标系中的坐标向量为Tw,则
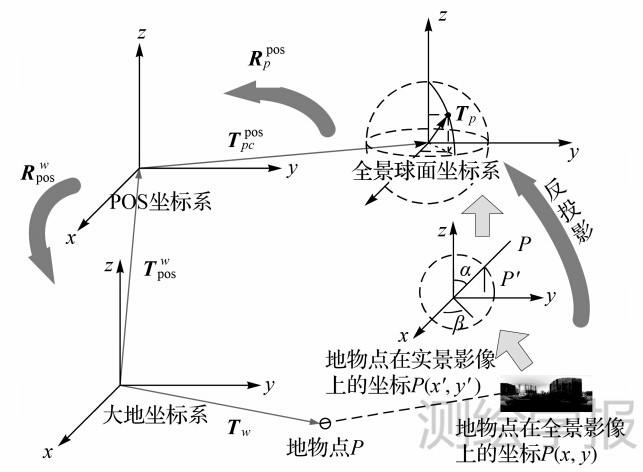
式(1)即为车载移动测图系统绝对定位方程。其中Tposw、Rposw表示POS系统相对大地坐标系的平移和旋转参数,是已知量,利用软件Inercial Explorer对GPS/IMU数据联合处理后可获得POS相对大地坐标系的姿态向量Oposw=[rposwpposwhposw]T,而Rposw可由姿态向量的3个分量来表达
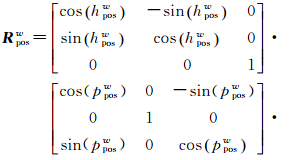
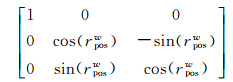
 |
| 图 3 车载移动测图系统外方位元素标定原理示意图 Fig. 3 Principles of extrinsic calibration for vehicle-based MMS |
由于获得的全景影像分辨率不一致,存在扭曲现象,无法直接在全景影像上选择控制点,参与标定计算。为此,构建全景球面模型(见图 3),将全景影像通过球面投影反变换投影到该球面模型上,从球面模型上直接点选获取控制点在全景影像上的球面坐标,参与标定运算。
如图 3,设地物点P在球面全景影像上坐标为P(x,y),则利用反投影公式(2)[17,18],可将其转换为球面空间视线为(ɑ,β)的全景影像拼接前的实景影像上的一点P′(x′,y′)
式中,α表示俯仰;β表示水平;f表示焦距。利用式(3),将(x′,y′)转化为世界坐标系下的坐标Ts=xsyszsT
按照透视投影方法,利用式(4)将Ts=[xsyszs]T转换为全景球面模型坐标系中的一点Tp=xpypzpT
式中,
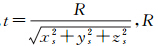 表示全景球面模型的半径。
3.2 标定参数的求解
表示全景球面模型的半径。
3.2 标定参数的求解
选择一定数量的控制点,利用控制点在大地坐标系的已知坐标和全景球面模型坐标系下的观测值坐标,结合矩阵形式,利用旋转矩阵的正交性确定Tpcpos、Rppos。
(1) 求解旋转矩阵Rppos
将式(1)的向量形式表达为矩阵形式如下
对标定点的坐标进行零均值化处理,设一个拍摄位置J有n个控制点,其在大地坐标系和全景球面模型坐标系中的质心坐标为Twg=
将均值化处理后的坐标T'w、T'p代入式(1),可以将绝对定位方程简化,并得到式(6)
将
由于旋转矩阵正交性对矩阵元素来说是非线性约束,给求解带来困难,借鉴文献[19, 20]中提到的罗德里格矩阵,将旋转矩阵Rwp表示为
计算可得X=(BTB)-1BTL,罗德里格参数求出后,利用
(2) 求平移量T
将Rwp代入方程(1),类似的,可建立偏移量的误差方程V′=B'T
4 试验及结果分析
遵循标定场地设计的一般原则[21],选择航天城作为标定场,该地区地势开阔,GPS信号良好,检校场有大量人工建筑设施(如建筑物、灯杆)且建筑物楼高合理、分布合理,便于从多个方位观察控制点。现场布设约100个控制点,采用安置于高精度已知点的全站仪测量得到,用于安置全站仪的已知点采用GPS静态测量得到,所用GPS及全站仪所测坐标测量精度达毫米级。这些控制点,分别用于全景相机的标定、激光扫描仪的标定、系统精度的检核。用于全景相机外方位元素标定的控制点分布如图 4所示。标定试验中选取24个控制点进行解算,10个控制点用于检核。控制点在大地坐标系下的坐标见表 1,控制点在全景球面模型坐标系下的坐标见表 1。
将表 1中前24个控制点测量数据,应用3.2节中的标定参数求解方法,可以得到标定结果(见表 2)。
在得到标定参数后,将全景影像上10个用于检核的控制点在全景球面模型坐标系下的坐标,应用标定参数,计算出这些用于检核的控制点对应的大地坐标系中的坐标,从而计算出残差并绘制其残差图(见图 5)。
从图 5中可知,检查控制点X方向最小及最大残差分别为0.377mm、8.746mm;Y方向最小及最大残差分别为0.508mm、2.574mm;Z方向最小及最大残差分别为0.170mm、-4.091mm;根据误差理论,计算的检验精度为:X、Y、Z的3个方向实际中误差分别为3.509mm、1.601mm、2.042mm。
为验证标定结果的可靠性,在标定场选取约3km的路段,选择分布均匀、特征明显的70个控制点。一方面,利用标定后的带有地理参考的全景影像序列,基于三角测量的原理[22],解算出控制点的大地坐标,并与实测结果对比,结果表明,在GPS信号良好的标定场,点的绝对定位中误差为平面10.3cm、高程16.5cm,距离量测的相对误差最大为4cm左右。另一方面,将实测控制点坐标反算到全景球面模型上,并将其法线与全景影像上的控制点的法线方向进行对比。图 6为路边的街灯反算到不同测站序列全景影像上的效果图。从图 6中可以看出,实测控制点反算到球面全景模型上的控制点法线方向与全景影像上控制点的法线方向基本重合。
此外,在天津滨海新区全景影像采集的实际项目中也进行了精度验证。选择GPS信号质量不同的实际道路,利用标定后的全景影像序列对道路两边的广告牌进行三角量测,并与实测结果对比,结果表明,在GPS信号不好的地区,点的绝对定位中误差约为平面35.4cm、高程54.8cm,点的相对量测误差最大为5cm。在较短的距离范围内(<3km),GPS信号质量对相对量测结果没有明显影响。
为进一步验证标定结果的可靠性,将全景影像和同一时刻的激光点云进行配准融合(如图 7),从图 7中可以清楚地看到,房屋、灯杆等地物点云和全景融合较好,可以满足基于多传感器融合的应用。
本文针对由全景相机和POS组成的车载移动测图系统外方位元素的标定进行了研究和试验。根据多相机拼接式的Ladybug3全景相机采用鱼眼镜头球面成像且所得全景影像分辨率不一致的特点,提出构建全景球面模型,将全景影像反投影到全景球面模型中,实现从该球面模型上的直接点选获取控制点,进行外方位元素标定的方法。试验结果表明,实际采集环境中,GPS信号良好时,点的绝对定位中误差为平面10.3cm、高程16.5cm,点的相对量测误差最大为4cm。GPS信号不好时,点的绝对定位中误差约为平面35.4cm、高程54.8cm,点的相对量测误差最大为5cm。并通过实地场景试验,得出在较短的距离范围内(<3km),GPS信号质量对相对量测的结果没有明显影响的结论。多传感器融合的三维真实场景的重建及灾害应急管理应用是下一步研究方向。
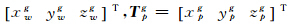 ,则Twg=
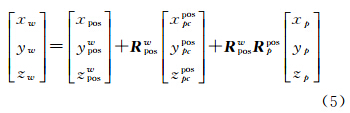
,则Twg=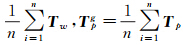 。记Tw、Tp经过均值化处理后的坐标为T'w=[X′wY′wZ′w]T,T'p=[X′pY′pZ′p]T,则T'w=Tw-Twg,T'p=Tp-Tpg。
。记Tw、Tp经过均值化处理后的坐标为T'w=[X′wY′wZ′w]T,T'p=[X′pY′pZ′p]T,则T'w=Tw-Twg,T'p=Tp-Tpg。 代入式(6),则
代入式(6),则
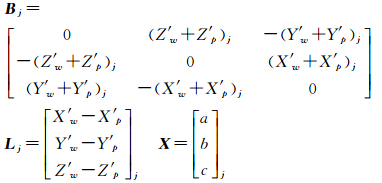
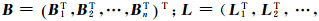
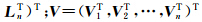 。
。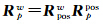 可以反算出Rppos。
可以反算出Rppos。
图 4 控制点分布图
Fig. 4 Control points distribution
控制点号 控制点大地坐标
控制点球面坐标 东 北 高 球面坐标X 球面坐标Y 球面坐标Z P001 435672.197 4437186.011 39.549 -0.7094730 -0.6098231 0.3532192
P002 435671.905 4437187.176 39.543 -0.8144940 -0.4465022 0.3704531
P003 435671.586 4437188.297 39.527 -0.8907151 -0.2581220 0.3741652







全景相机相对POS系统 平移参数/m 旋转参数/(°) X Y Z r p h P至POS 0.068588 0.027610 0.077613 0.020006 0.007467 -0.027595

图 5 检查点残差图
Fig. 5 Residual error plot for checking points 
图 6 街灯顶点反算到全景球面模型在不同测站全景影像上法线重合的效果图
Fig. 6 Reverse calculation for the top of the lamp-post in different geo-referenced panoramic images at different mobile surveying spots 
图 7 全景影像和激光点云配准融合效果图
Fig. 7 Registration fusion for panorama and laser-point clouds
| [1] | CHEN T, YAMAMOTO K, CHHATKULI S, et al. Panoramic Epipolar Image Generation for Mobile Mapping System[C]//International Archives of the Photogrammetry,Remote Sensing and Spatial Information Science.Melbourne:[s.n.],2012. |
| [2] | YE Zetian,YANG Yong, ZHAO Wenji, et al.Dynamic Calibration of Exterior Orientations for Vehicle GPS/IMU/LS Laser Imaging System[J].Acta Geodaetica et Cartographica Sinica,2011,40(3):345-350.(叶泽田,杨勇,赵文吉,等.车载GPS/IMU/LS激光成像系统外方位元素的动态标定[J].测绘学报,2011,40(3):345-350). |
| [3] | ZHENG Shunyi, HUANG Rongyong, GUO Baoyun, et al. Stereo-camera Calibration with Restrictive Constraints[J].Acta Geodaetica et Cartographica Sinica,2012,41(6):877-885.(郑顺义,黄荣永,郭宝云,等. 附约束条件的立体相机标定方法[J].测绘学报,2012,41(6):877-885). |
| [4] | THIBAULT S, PARENT J, ZHANG H, et al. Developments in Modern Panoramic Lenses: Lens Design, Controlled Distortion and Characterization[C]//Proceedings of the International Society for Optical Engineering.Beijing:[s.n.],2011. |
| [5] | SHUNPING J, YUN S, ZHONG C S. Bundle Adjustment with Vehicle-based Panoramic Imagery[C]//Proceedings of Second International Workshop on Earth Observation and Remote Sensing Applications. [S.l.]: IEEE, 2012: 106-110. |
| [6] | ZHANG Q, PLESS R. Extrinsic Calibration of a Camera and Laser Range Finder (Improves Camera Calibration)[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. [S.l.]: IEEE, 2004, 3: 2301-2306. |
| [7] | PANDEY G, MCBRIDE J, SAVARESE S, et al. Extrinsic Calibration of a 3D Laser Scanner and an Omnidirectional Camera[C].Proceedings of the 7th IFAC Symposium on Intelligent Autonomous Vehicles. Michigan: [s.n.], 2010. |
| [8] | MIRZAEI F M, KOTTAS D G, ROUMELIOTIS S I. 3D LiDAR-camera Intrinsic and Extrinsic Calibration: Identifiability and Analytical Least-squares-based Initialization[J]. The International Journal of Robotics Research, 2012, 31(4): 452-467. |
| [9] | LI G, LIU Y, DONG L, et al. An Algorithm for Extrinsic Parameters Calibration of a Camera and a Laser Range Finder Using Line Features[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. [S.l.]: IEEE, 2007: 3854-3859. |
| [10] | RODRIGUEZ F, FREMONT V, BONNIFAIT P. Extrinsic Calibration between a Multi-layer LiDAR and a Camera[C]//Proceedings of IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems[S.l.]: IEEE, 2008: 214-219. |
| [11] | AMIRI PARIAN J, GRUEN A. Sensor Modeling, Self-calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 60-76. |
| [12] | AHOUANDJINOU A S R M, EZIN E C, MOTAMED C, et al. An Approach to Correcting Image Distortion by Self Calibration Stereoscopic Scene from Multiple Views[C]//Proceedings of Eighth International Conference on Signal Image Technology and Internet Based Systems. [S.l.]: IEEE, 2012: 389-394. |
| [13] | GONG X, LIN Y, LIU J. Extrinsic Calibration of a 3D LiDAR and a Camera Using a Trihedron[J]. Optics and Lasers in Engineering, 2012,51(4):394-401. |
| [14] | GONG X, LIN Y, LIU J. 3D LiDAR-Camera Extrinsic Calibration Using an Arbitrary Trihedron[J]. Sensors, 2013, 13(2): 1902-1918. |
| [15] | GREJNER-BRZEZINSKA D A, LI R, HAALA N, et al. From Mobile Mapping to Telegeoinformatics: Paradigm Shift in Geospatial Data Acquisition, Processing, and Management[J]. Photogrammetric Engineering and Remote Sensing, 2004, 70(2): 197-210. |
| [16] | GREY.P.Ladybug3 Technical Reference Manual[EB/OL].[2013-08-12]. http://ww2.ptgrey.com/products/ladybug3/. |
| [17] | FENG Haibo.The Realization of the Panoramic-image Maker of Virtual Panoramic Space System[D].Chengdu: University of Electronic Science and Technology of China, 2007.(冯海波. 虚拟全景空间生成技术研究与实现[D]. 成都:电子科技大学, 2007.) |
| [18] | HRENEK D, KUSST J. MIKSA N,et al.Tiled 360deg Panoramic Projection System[C]//Proceedings of the 35th International Convention on Information and Communication Technology, Electronics and Microelectronics. Opatija: [s.n.], 2012: 1793-1797. |
| [19] | ZHANG Ka,SHENG Yehua,YE Chun,et al. Absolute Calibration and Precision Analysis for Vehicle-borne 3D Data Acquiring System Integrated with GPS,INS and CCD-camera[J].Geomatics and Information Science of Wuhan University,2008,33(1):55-59.(张卡,盛业华,叶春,等.车载三维数据采集系统的绝对标定及精度分析[J].武汉大学学报:信息科学版,2008,33(1):55-59.) |
| [20] | ZHANG Jun,LIU Jian,LIU Xiaomao.Three Dimensional Absolute Orientation Model Using the Roderick Matrix[J].Infrared and Laser Engineering, 1998,27(4):30-32. (张钧,柳健,刘小茂.利用罗德里格矩阵确定三维表面重建中的绝对定向模型[J]. 红外与激光工程, 1998, 27(4): 30-32.) |
| [21] | ZOU Xiaoliang,ZHANG Yongsheng. Digital Camera's Boresight Angle Calibration Method of Mobile Mapping System for Land Vehicles[J]. International Workshop on Terrestrial LiDAR Static to Mobile,2010:99-104. |
| [22] | FENG Wenhao.Close-range Photogrametry[M].Wuhan:Wuhan University Press,2002. (冯文灏.近景摄影测量学[M].武汉:武汉大学出版社,2002.) |