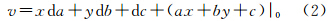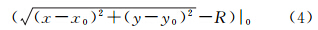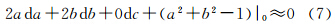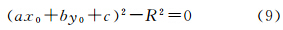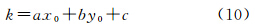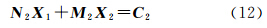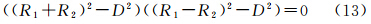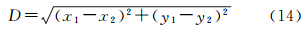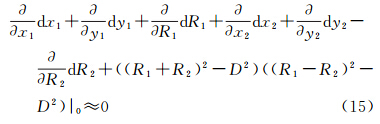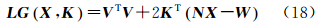2. 武汉大学遥感信息工程学院,湖北 武汉 430079
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
我国是零部件制造大国,但产品质量检测方面却长期没有得到重视,许多国内企业仍然采用人工检验方式检验零件质量,效率低下,常因人为失误导致漏检错检,给厂商带来巨大的损失,而且无法有效建立质量反馈系统。国家中长期科技发展规划(2006-2020)[1]中特别提出要重点研究开发高精度零件检测仪器。由于视觉测量技术具有速度快、无接触等优点[2],因此成为当前零件制造与自动化、近景摄影测量、计算机视觉等领域的重要研究方向。本文在零件质量视觉检测的研究过程中,对零件轮廓线多特征提取进行的相关研究。
在零件视觉检测过程中,经过图像边缘提取后,从待测零件图像可以得到平面轮廓像素点集合,属于同一个图元的轮廓像素点集合可构成如直线、圆弧等基本几何图元[3]。二维测量中在对零件形状尺寸等参数检测时,一般都是根据图元的尺寸、形状和各图元的位置关系等进行检测,因此检测前必须先识别出组成零件轮廓的各图元的特征。三维测量中,也有利用零件的轮廓线进行视觉测量重建的研究[4,5],所以对轮廓基本图元进行精确地分割识别是视觉检测过程中一个关键步骤,会直接影响零件尺寸测量的准确性。
图元与图元间的分割点称为特征角点[3],它们可能是直线与直线或直线与圆弧等的邻接点。识别图元特征要先检测出零件轮廓的特征角点,从而获取图元与图元的连接点,然后根据相邻特征角点的类型来确定图元的类型,因此特征角点的检测是轮廓多特征图元识别的关键。国内外很多学者对此进行了广泛而深入的研究,例如文献[9]结合曲率、投影高度、合并分裂等方法提取特征角点,实现了用圆弧和直线等图元描述轮廓的特征信息,但在提取过程中没有充分利用图元间存在的固有关系(如相切关系),这必然会影响角点提取的精确度。
考虑到工业零件加工的特点,本文在综合利用已有轮廓特征角点检测方法的基础上加入相关约束条件,实现利用直线和圆弧来对轮廓进行精确分割(文献[10]已证明仅用直线和圆弧就可以很好地表达常见零件的轮廓信息):首先介绍自适应k曲率法[11,12]分割特征、点投影高度法[6,13,14]识别特征及特征间的逻辑关系来分割或合并特征点的方法,然后利用轮廓上圆弧与直线相切、相邻圆弧与圆弧相切等约束条件,对轮廓上的特征进行迭代精确提取,最后用试验证明了添加约束条件后,轮廓多特征提取更加准确可靠。 1 轮廓特征初始提取
由于视觉检测系统一般都会设置成半封闭的环境,具有良好照明条件,因此获取的待测对象的影像质量一般都较好,目标与背景间的对比度大,利用一般的边缘提取[15,16,17]再进行细化[18]的方法就能获取零件的初始轮廓,得到初始轮廓后利用八邻域跟踪方法[19,20]获取按照从起点到终点顺序排列的轮廓像素点集合。在提取轮廓特征角点前,为减少运算量,先采用邻域值对比的方法[3,6]预先分类轮廓点,将不可能为角点的轮廓点去掉,对保留下来的轮廓点本文将介绍利用旋转不变的角点判定方法及基于角度判定方法[6]去除因直线重采样导致的冗余角点,最后能得到如图 1所示的角点提取结果。
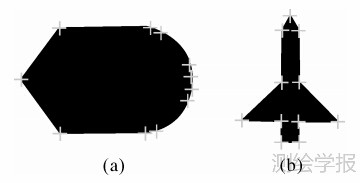 |
| 图 1 轮廓特征角点初始提取结果 Fig. 1 Initial extraction results of outline corner |
从图 1(a)可以看出圆弧上仍然有很多冗余角点需要去除,去除方法为:首先根据角点邻域特征将角点分为两种类型,第1种是突变角点(C类型),角点两侧曲线段属于不同特征(如图 2(a)、(b)),第2种是平滑角点(S类型),它可能为直线与圆弧的相切点或者圆弧上的冗余角点(如图 1(a)右边圆弧部分及图 2(c)、(d)所示),其两侧曲线段可能属于同一特征,可能需要去除;然后利用自适应k曲率法[7,9]来区分角点类型。
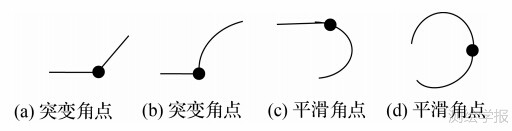 |
| 图 2 角点类型示例 Fig. 2 Corner types |
要对轮廓基本图元进行分段识别,还要确定图元的类型,即判断图元是直线还是圆弧。本文将基于点投影高度[6]方法判别两轮廓角点间的图元类型,从而进一步将角点分为以下4种类型:①ll型,即直线至直线(line to line);②al型,即圆弧至直线(arc to line);③la型,即直线至圆弧(line to arc);④aa型,即圆弧至圆弧(arc to arc)。
考虑与前面的C型和S型组合,本文最终将角点分为以下几类:c_ll、c_la、c_aa、c_al、s_la、s_al和s_aa 7个子类。如s_al表示连接圆弧和直线的平滑角点,c_al表示连接圆弧和直线的突变角点。对于平滑性特征角点,则其两端曲线段有可能属于同一个特征而被合并。
图元参数的识别是根据轮廓段两端点的角点类型来确定的,但在特征角点检测中难免会有遗漏。如图 3所示,ll角点紧接着就是aa角点,根据逻辑关系知道ll和aa之间肯定存在la角点,所以这时需要在两者之间插入la角点,方法如下:用直线连接ll角点和aa角点,然后从ll角点和aa角点间的轮廓点中找出到这两个角点连线距离最远的点(max_h),即该点为插入的la角点。
 |
| 图 3 需要插入新角点的情况 Fig. 3 Cases that needed to insert new corners |
对于图 4(a)有连续的圆弧特征的情况需要判断其相互间是否能被合并或需要被分割。首先估算出圆弧的圆心和半径,然后利用每点到圆心的距离与半径差值的和与该段圆弧长度的比值η的圆弧判别函数[6],依据下面的准则合并或分裂圆弧:当两段圆弧合并之后的η值更小时,则合并两端圆弧;当插入一个aa角点后,计算出的η值更小时则分割圆弧。最后得到图 4(b)的结果。
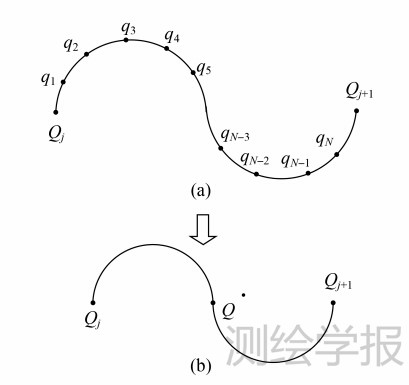 |
| 图 4 圆弧分裂与合并示意图 Fig. 4 Schematic arc splitting and merging |
当识别出轮廓上的特征角点后,就可以将零件轮廓用直线和圆弧表示。ll型和la型角点间的曲线段用直线表达,la型和aa型角点间的曲线段用圆弧表达。 2 附约束条件的零件轮廓多特征参数整体求解
由于已有研究[10]证明仅用直线和圆弧就可以很好地表达自由轮廓信息,因此本文以只包含直线和圆弧的轮廓来描述如何进行附加约束条件的多图元特征的联合提取。计算过程具体如下: 2.1 基本条件
(1)直线方程表达式为
则其误差方程为 (2)圆的方程表达式为 则其误差方程为 用矩阵表示以上两类误差方程,得到 式中,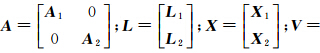
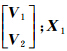 表示所有直线参数组成的向量;X2表示所有圆参数组成的向量;A1表示所有直线观测误差方程系数组成的系数矩阵;L1为相应的常数项向量;V1则为相应的残差向量;A2表示所有圆观测误差方程系数组成的系数矩阵;L2为相应的常数项向量;V2则为相应的残差向量。
2.2 约束条件
表示所有直线参数组成的向量;X2表示所有圆参数组成的向量;A1表示所有直线观测误差方程系数组成的系数矩阵;L1为相应的常数项向量;V1则为相应的残差向量;A2表示所有圆观测误差方程系数组成的系数矩阵;L2为相应的常数项向量;V2则为相应的残差向量。
2.2 约束条件(1) 对于直线方程一般形式来说,a,b代表的是直线的法向量,因此直线参数a和b满足
线性化可以得到
对这一类约束条件,将式(7)写成矩阵形式为
式中,N1为其系数矩阵;C1为相应的常数向量。(2) 圆弧和直线相切的约束条件
令
则其线性化形式为对此类约束条件可以写成矩阵形式
式中,N1和M2分别为X1和X2对应的系数矩阵;C2是相应的常数向量。(3) 圆弧与圆弧相切的约束条件
令两个圆弧参数分别为(x1,y1,R1),(x2,y2,R2)则其相切条件为(同时包括内切和外切)
式中该约束条件的线性化形式为
将这些约束条件写成矩阵形式(所有的(式15)形式的约束条件),则为
式中,M3为系数矩阵;C3则为常数向量。令

引入辅助的拉格朗日系数K,构造朗格朗日函数如下
利用拉格朗日求极值的准则,对LG(X,K)求各个参数的偏导数并令其为零,可以得到如下的法方程
将所有轮廓点根据具体情况按式(5)、式(8)、式(12)、式(16)计算矩阵A、N、L和W,然后代入式(19),即可迭代求解获得轮廓各图元特征的精确参数值。 3 试验结果与分析
为了验证附加约束条件的有效性,分别采用模拟图像和实际零件图像进行验证试验。
对本文提出方法的准确性需要进行定量的分析,而实际试验中无法获得实际零件的真实值,所以本文根据已知零件尺寸设计图绘制了模拟图像进行验证试验。对于模拟图像,本文方法的提取结果如图 5(a)、图 5(b)所示,包含5条直线、2段圆弧和3个圆,其中对于两段圆弧的提取结果,附约束条件和未附约束条件的提取值与模拟设计值的比较见表 1。从表 1的对比中可以发现约束条件的引入使得提取结果更加准确,从而定量地说明了本文方法是有效的。
 |
| 图 5 模拟图像轮廓图元特征角点提取结果 Fig. 5 Contour corner features extraction results of analog image |
| 图 5中的5号特征(圆弧) | 图 5中的6号特征(圆弧) | |||||||
| x0 | y0 | r | sita | x0 | y0 | r | sita | |
| 设计值 | 633.85 | 147.30 | 132.10 | 179.50 | 501.65 | 399.40 | 118.85 | 44.50 |
| 未附约束条件测量值 | 633.722 | 146.920 | 132.295 | 179.420 | 501.676 | 399.910 | 118.295 | 44.452 |
| 附约束条件测量值 | 633.870 | 147.287 | 132.094 | 179.429 | 501.665 | 399.381 | 118.841 | 44.468 |
| 未附约束条件的 测量值与设计值之差 | -0.128 | -0.38 | 0.195 | -0.08 | 0.026 | 0.51 | -0.555 | -0.048 |
| 附约束条件测量值 与设计值之差 | 0.02 | -0.013 | -0.006 | -0.071 | 0.015 | -0.019 | -0.009 | -0.032 |
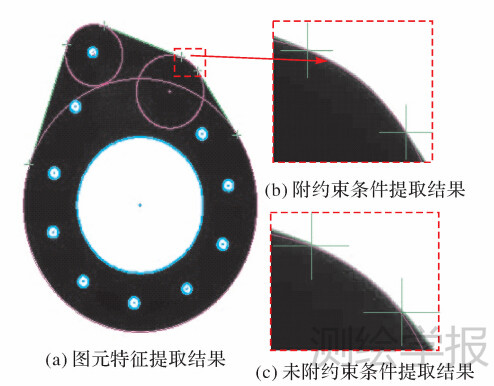
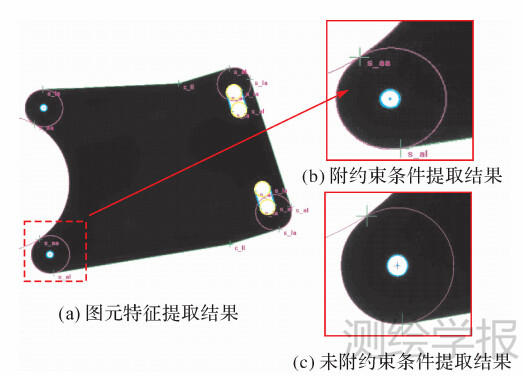
对于实际零件图像,本文利用工业相机和大口径远心镜头获取的一些具有代表性的零件图像进行验证。利用本文方法对图像上零件轮廓提取结果如图 6、图 7、图 8(a)及图 9(a)所示。这些结果表明,本文方法均能正确地提取轮廓图元间的分割角点,甚至对于连续圆弧相邻接情况的零件,也能准确地提取圆弧相切点作为分割点(见图 9)。此外从图 8(b)、图 8(c)、图 9(b)、图 9(c)及图 10的细节对比图中可以看出附加约束条件的轮廓图元特征分割角点的提取位置更加准确合理。
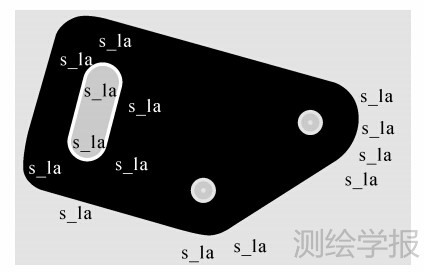 |
| 图 6 实际零件图像轮廓图元特征分割角点提取结果 Fig. 6 Contour segmentation corner extraction results of actual part feature |
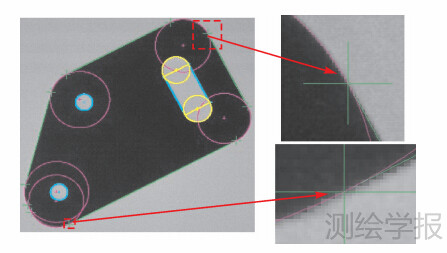 |
| 图 7 实际零件图像轮廓图元特征提取结果及细节放大 Fig. 7 Contour feature extraction result of actual part features and enlargement details |
 |
| 图 8 有较大圆弧情况的零件图像轮廓图元特征提取结果及附约束和未附约束情况下的角点提取细节对比 Fig. 8 Contour feature extraction result of actual part features with large contour arc situation and corner position extraction comparison between cases with and without attached constraints |
 |
| 图 9 有圆弧相邻接情况的零件图像轮廓图元特征提取结果细节图及附约束和未附约束情况下的角点提取细节对比 Fig. 9 Contour feature extraction result of actual part features with arc adjacent parts situation and corner position result comparison between with and without attached constraints cases |
 |
| 图 10 未附约束条件和附约束条件情况下提取的角点位置对比 Fig. 10 Corner position extraction comparison between cases with and without attached constraints |
本文介绍了一种附加约束条件的边缘轮廓多特征提取方法,即在已有方法提取的多特征结果的基础上附加轮廓上圆弧与直线相切、相邻圆弧与圆弧相切等约束条件来对轮廓特征进行整体精确求解,将组成轮廓的各特征如直线、圆弧、圆,进行精确分段识别,获得各特征的精确参数。最后使用模拟图像和多组零件的真实影像进行了试验验证。结果表明使用本文方法都能正确地提取出组成轮廓的各个图元特征,并且提取出的角点的位置比未加约束条件的情况下提取出的角点的位置更加准确可靠。
| [1] | The State Council of the People's Republic of China. The Medium and Long-term National Planning Outline of Science and Technology Development (2006-2020) [EB/OL]. 2006[2013-06-23]. http://www.mlr.gov.cn/kjgl/201005/t20100517_149200_3.htm. (中华人民共和国国务院.国家中长期科技发展规划纲要(2006-2020)[EB/OL]. 2006[2013-06-23]. http://www.mlr.gov.cn/kjgl/201005/t20100517_149200_3.htm.) |
| [2] | YE Shenghua, ZHU Jigui, WANG Zhong, et al. Visual Inspection Technology and Its Application[J]. China Engineering Science, 1999, 1(1):49-52.(叶声华, 邾继贵, 王仲, 等. 视觉检测技术及应用[J]. 中国工程科学, 1999, 1(1): 49-52.) |
| [3] | WU Jigang, BIN Hongzan. Research on Planar Contour Primitive Recognition Method Based on Curvature and HOUGH Transform[J]. Journal of Electronic Measurement and Instrument, 2010(1): 124-130.(伍济钢, 宾鸿赞. 基于曲率与HOUGH变换的平面轮廓图元识别方法研究[J]. 电子测量与仪器学报, 2010(1): 124-130.) |
| [4] | ZHENG Shunyi, SUN Mingwei. 3D Visual Measurement and Reconstruction Based on Object's Profile in Images[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 353-357.(郑顺义, 孙明伟. 基于物体成像轮廓的视觉测量与重建[J].测绘学报, 2006, 35(4): 353-357.) |
| [5] | ZHENG Shunyi, GUO Baoyun, LI Cailin. 3D Reconstruction and Inspection of Cylinder Based on Geometric Model and Generalized Point Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 477-482.(郑顺义, 郭宝云, 李彩林. 基于模型和广义点摄影测量的圆柱体自动三维重建与检测[J]. 测绘学报, 2011, 40(4): 477-482.) |
| [6] | SHEU H T, HU W C. A Rotationally Invariant Two-phase Scheme for Corner Detection[J]. Pattern Recognition, 1996, 29:819-828. |
| [7] | HU W C. Multiprimitive Segmentation Based on Meaningful Breakpoints for Fitting Digital Planar Curves with Line Segments and Conic Arcs[J]. Image and Vision Computing, 2005, 23(9): 783-789. |
| [8] | KOLESNIKOV A. Segmentation and Multi-model Approximation of Digital Curves[J]. Pattern Recognition Letters, 2012, 33: 1171-1179. |
| [9] | WU Jigang. Research on Key Technologies in Dimensional Inspection System of Thin Sheet Parts Based on Machine Vision[D]. Wuhan: Huazhong University of Science and Technology. 2009.(伍济钢. 薄片零件尺寸机器视觉检测系统关键技术研究[D]. 武汉:华中科技大学, 2009.) |
| [10] | ROSIN P L. Techniques for Assessing Polygonal Approximations of Curves[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19: 659-666. |
| [11] | MOKHTARIAN F, SUOMELA R J. Robust Image Corner Detection Through Curvature Scale Space[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(12): 1376-1381. |
| [12] | MOKHTARIAN F, SUOMELA R. Enhancing the Curvature Scale Space Corner Detector[C]// Proceedings of Scandinavian Conference on Image Analysis. Bergen: [s.n.], 2001:145-152. |
| [13] | FARAGO F T. Handbook of Dimensional Measurement[M]. 2nd ed. New York: Industrial Press, 1982. |
| [14] | WU Q M, RODD M G. Boundary Segmentation and Parameter Estimation for Industrial Inspection[J]. IEEE Proceedings of Computers and Digital Techniques, 1990, 137(4): 319-327. |
| [15] | ZHANG Jing. Profile Measuring Techniques Study in the Entire Imaging Measuring Method[D]. Tianjin: Tianjin Univerisity, 2009.(张进. 完整成像测量方法中轮廓测量技术的研究[D]. 天津: 天津大学, 2009.) |
| [16] | ZHANG Xiang, LIU Meijie, CHEN Liwei. Method of Picking up Edge on the Basis of the Mathematics Morphologic Subject[J]. Journal of University of Electronic Science and Technology of China, 2002, 31(5): 492-495. (张翔, 刘媚洁, 陈立伟. 基于数学形态学的边缘提取方法[J].电子科技大学学报, 2002, 31(5): 492-495.) |
| [17] | WANG Fusheng, QI Guoqing. Boundary Tracking Algorithm of Objects in Binary Image[J]. Journal of Dalian Maritime University, 2006, 32(1): 62-67. (王福生, 齐国清. 二值图像中目标物体轮廓的边界跟踪算法[J].大连海事大学学报, 2006, 32(1): 62-67.) |
| [18] | LI Jie, PENG Yueying, YUAN Changan, et al. Edge Thinning Based on Mathematical Morphology Thinning Algorithm[J]. Journal of Computer Applications, 2012(2): 514-520. (李杰, 彭月英, 元昌安, 等. 基于数学形态学细化算法的图像边缘细化[J]. 计算机应用, 2012(2): 514-520.) |
| [19] | LIU Xiangbin, XIANG Jianchi, YANG Bo. A Labeling Algorithm Based on 8-connected Boundary Tracking[J]. Computer Engineering and Applications, 2001(23): 125-132. (刘相滨, 向坚持, 阳波. 基于八邻域边界跟踪的标号算法[J].计算机工程与应用, 2001(23): 125-132.) |
| [20] | ZHANG Yujin. Image Processing and Analysis[M]. Beijing: Tsinghua University Press, 1999. (章毓晋. 图像处理和分析[M].北京: 清华大学出版, 1999.) |