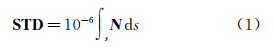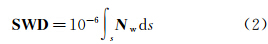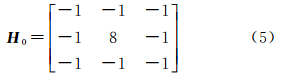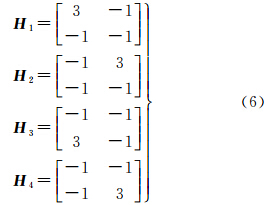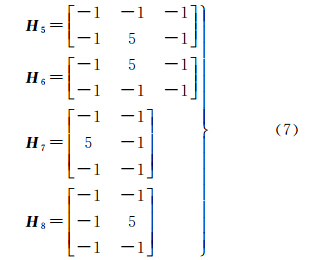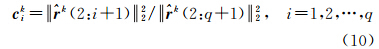2. 中国科学院测量与地球物理研究所,湖北 武汉 430077;
3. 中国科学院大学,北京 100049;
4. 武汉大学测绘学院,湖北 武汉 430079
2. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
自从文献[1]提出地基GPS水汽探测技术后,其高精度、全天候、高时空分辨率等优点在气象学内得到了广泛应用。地基GPS水汽探测所得的大气可降水量(precipitable water vapor,PWV)是测站天顶方向总的水汽含量,无法反映出水汽的三维分布,因此限制了它在天气分析和数值预报中的应用[2]。文献[3,4,5,6,7]研究表明,区域GPS 网各测站斜路径湿延迟含有一定的水汽三维分布信息,因此研究如何从斜路径水汽含量反演水汽三维分布具有较大的科研价值和实用意义。
文献[3]率先开展水汽层析方面的研究,采用SVD方法求解层析方程,并用ECMWF预报值验证结果;文献[4]分析了约束条件对GPS水汽层析结果的影响,并证明初值对层析结果的可靠性有重要影响;文献[5]初步讨论了ART、SART、MART等在GNSS水汽层析中应用,并给出了经验松弛因子和迭代终止条件;文献[6]验证了ART、MART、SIRT用于对流层水汽层析的可行性,也给出了参考松弛因子和迭代终止参数。
由于测站几何分布、卫星星座、网格划分等因素的影响,层析方程系数矩阵往往稀疏且严重秩亏,导致其无法直接求解[5,6,7,8]。代数重构算法是一种线性反演方法,采用迭代的形式避免了法方程的求逆。本文研究了代数重构算法在水汽层析应用中的各种问题,如约束条件、松弛因子、终止条件等。本文首先介绍水汽层析原理,约束条件及层析方程构建,然后分析代数重构算法在层析方程求解中的各种问题,包括初值的选择、松弛因子的计算、迭代终止的确定等,并以香港SatRef网进行验证分析。 2 层析原理
GPS信号在传播过程中由于对流层的影响会造成一定的信号延迟(slant total delay,STD)[9,10,11,12,13,14,15],该延迟可表示为
式中,N为大气折射率,是静力学折射率Nd和湿折射率Nw之和,其中Nd可由地面气象观测值计算。由此可得由水汽引起的湿延迟 (slant wet delay,SWD) 通过高精度GPS数据处理软件解算出STD、SWD等,然后由SWD计算斜路径大气可降水量 (slant wet vapor,简称SWV)。得到SWV后,根据实际情况对观测方程进行离散化,即将研究区域空间划分网格。离散化后,观测方程变为 式中,A为系数阵;x表示网格水汽密度;d为斜路径水汽含量。 3 层析方程 3.1 约束条件前面已经提到层析方程是秩亏的,即大量网格没有GPS信号穿过。对于那些没有信号穿过的网格,方程解算的结果与初值一样。为了解决该问题,需引入平滑约束条件。 3.1.1 水平平滑约束
水汽在空间分布上具有连续性,根据地理学第一定律,距离越近的网格,相关性越大,故可定义平滑约束方程[16]
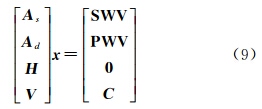
式中,H为水平平滑约束矩阵;l为约束条件数。考虑到水汽缓慢均匀的变化特性,可采用均值滤波器进行平滑处理[7]。对于那些处于研究区域中间的网格来说,约束条件由该网格所在层面周围8个网格的二阶Laplacian算子给出,即 对于处于探测平面边缘的网格来说,该算子必须要经过适当调整才能使用。这里给出每个平面顶点处的算子,分别为左上角H1,右上角H2,左下角H3,右下角H4对于那些处于边线而非顶点处的网格来说,该算子调整为上边线H5,下边线H6,左边线H7,右边线H8
在附加该水平平滑约束后,有多个信号穿过的网格将给临近网格提供改正值,没有信号穿过的网格将从其临近网格获取改正信息,从而使整体结果得到修正。 3.1.2 垂直约束探空资料提供的剖面信息显示水汽主要集中在6km以下,10km处水汽含量接近于零,因此将上边界的水汽密度强制约束为0.01g/m3。根据上述说明,构建垂直约束方程
3.2 层析方程构建根据以上约束条件和观测方程,构造出层析方程
式中,As为斜方向投影函数;SWV为斜路径水汽含量;Ad为天顶方向投影函数;PWV为天顶方向水汽含量;H表示水平约束条件;V表示垂直约束条件。 4 代数重构算法这里简单介绍代数重构算法中常用的8种算法,它们分别为Kaczmarz、Randkaczmarz、Symkaczmarz、SART、Landweber、Cimmino、CAV、DROP[5,17,18]。其中Kaczmarz、Randkaczmarz、Symkaczmarz算法都属于ART(algebraic reconstruction techniques)算法,区别仅在于内循环顺序不一样,Kaczmarz为依次循环,Randkaczmarz为随机循环,而 Symkaczmarz包括一次顺序循环和一次逆序循环[10]。而SART、Landweber、Cimmino、CAV和DROP算法都属于SIRT(simultaneous iterative reconstruction techniques)算法,与ART算法的不同在于它不再单独对每条观测路径上的网格逐个进行修正,故没有内循环,而是一次性对所有观察路径进行迭代。各算法的具体计算公式请查阅相关参考文献,限于篇幅,这里不做详细介绍。 5 层析方程求解 5.1 迭代初值选取
文献[4]的研究表明,水汽层析结果的可靠性在很大程度上依赖于先验信息的精度,因此初值的选择也是代数重构算法的重要部分。对于水汽的层析解算,初值的获取一般有以下3种方式:①利用无线电探空仪提供的大气廓线信息,该方法精度最高;②利用数值预报模型的计算结果,该方法也较准确;③直接利用标准大气分布模型,该方法精度较差。 5.2 松弛因子选择
松弛因子在迭代中起到调节改正量的作用,影响着收敛速度和迭代结果的质量。文献[5]证明,松弛因子的选择甚至比算法还重要。这里介绍一种计算最优松弛因子的方法[5,17,18],松弛因子能以最快的速度收敛到最小方差,计算松弛因子需要一定的先验知识。
该算法[18]由两步组成,首先确定能获取整体最小方差所有可行的λ,然后确定能通过最少的迭代次数就能达到该最小方差的λ。如果用ηλ表示对应给定λ的最小方差,则由于迭代的离散本质,ηλ会随着λ的变化而缓慢变化,但是对于不同的λ,ηλ的偏差很小。以SIRT算法为例,试验发现,若要达到整体方差最小,λSIRT=1/ρ(ATMA)比较合适,则可定义最小方差的上限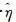 =1.01ηλSIRT。
=1.01ηλSIRT。
假设kλ是给定的松弛因子λ为达到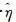 所需要的迭代次数,接下来就是在最小化kλ中计算出最优的λ。试验表明kλ是λ的单峰函数,故可用以下经过改进的黄金分割搜索法来计算最优的λ。该方法首先给定λ一个初始搜索域(α,β),即SIRT的收敛区间,然后计算出两个初始内部点α′=α+r(β-α)和β′=α+(1-r)(β-α),其中r=(3-5)/2。假定此时的迭代次数为κα′和κβ′,相关的最小方差为ηα′和ηβ′,然后根据以下判断来缩小搜索区间。
所需要的迭代次数,接下来就是在最小化kλ中计算出最优的λ。试验表明kλ是λ的单峰函数,故可用以下经过改进的黄金分割搜索法来计算最优的λ。该方法首先给定λ一个初始搜索域(α,β),即SIRT的收敛区间,然后计算出两个初始内部点α′=α+r(β-α)和β′=α+(1-r)(β-α),其中r=(3-5)/2。假定此时的迭代次数为κα′和κβ′,相关的最小方差为ηα′和ηβ′,然后根据以下判断来缩小搜索区间。
ηα′>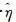 :最小方差λ=α′没有达到整体最小方差水平,将区间缩减到(α′,β)。
:最小方差λ=α′没有达到整体最小方差水平,将区间缩减到(α′,β)。
ηβ′>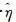 :最小方差λ=ηβ′没有达到整体方差最小值,将区间缩减到(α,β′)。
:最小方差λ=ηβ′没有达到整体方差最小值,将区间缩减到(α,β′)。
κα′≥κβ′:α′和β′对于λ都是可行的值,根据单峰性,将区间缩减到(α′,β)。
κα′<κβ′:α′和β′对于λ都是可行的值,根据单峰性,将区间缩减到(α,β′)。
按照上述步骤循环搜索松弛因子,直到其所在的区间宽度足够小(如10-6),然后以区间中点为最优的λ。该训练算法对于ART算法也类似,但是对于Randkaczmarz方法,由于内循环指数i的前后不一致性,故需要通过试验来获取不同的λ。此外,在实现该训练算法中需设定最大循环数kmax,这是由于对于某些问题,可能没有在指定的循环数内达到最小方差,此时就需要在k=kmax下确定能够达到最小方差的最优松弛因子。 5.3 迭代终止条件
代数重构算法需要通过迭代来达到试验数据的响应,考虑到有可能迭代到某一个点后结果变差,或出现参数震荡,因此必须确定达到试验数据的最佳响应时刻,从而最优的结束循环[5,18,19,20]。一种方式是当结果趋于稳定,即当xk+1和xk 两者之差小于某个阈值时结束;另一种方式是当|Axk-mk |=min时结束循环[5]。但这些标准并不适用于该问题,为此,文献[5,6]定义了一系列参数作为判断迭代终止的依据。
本文采用正规化累积周期图(normalized cumulative periodogram,NCP)作为迭代终止条件[18,19,20],接下来详细介绍该方法。在NCP中,将每次迭代的剩余量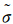 看作时间序列,由于其表示的信号与白噪声有着明显不同,因此可以判断出最优迭代数k。定义k ∈Cm为rk的离散傅里叶变换,q为满足q≤m/2的最大整数,则rk的NCP元素(Ck ∈Rq)为
看作时间序列,由于其表示的信号与白噪声有着明显不同,因此可以判断出最优迭代数k。定义k ∈Cm为rk的离散傅里叶变换,q为满足q≤m/2的最大整数,则rk的NCP元素(Ck ∈Rq)为
如果rk由白噪声构成,则其期望功率谱为平的,期望NCP元素位于从(0,0) 到 (q,1)的直线上。实际噪声的功率谱没有理想中的平坦,但NCP元素分布仍然接近于直线。该问题的关键在于确定剩余量从信号主导到白噪声主导的迭代数目k[19,20],一旦rk呈现出白噪声的分布特点,即NCP分布接近于直线,迭代就可以终止。决定rk是否为白噪声的计算是实际NCP元素的Kolmogorov-Smirnoff检验,若实际的NCP元素位于理论NCP元素的Kolmogorov-Smirnoff区间内,则表示可接受rk为白噪声这个假设,表明此时迭代可终止,从而可以确定出最佳迭代数kopt。若假设检验的显著性水平为5%,则Kolmogorov-Smirnoff区间的界线为±1.36q-1/2。 6 试验分析
试验采用香港卫星定位参考站网(SatRef)提供的2012年148~155d的数据,用GAMIT进行解算,引入BJFS、SHAO和KUNM 3个IGS站,卫星高度截止角取为10°,天顶静力学延迟采用Saastamoinen模型,对流层延迟采用线性估计模型,映射函数采用VMF1模型。层析试验中,将研究区域划分为6×6×10=360个网格,如图 1所示,采用京士柏气象站(HKKP)的无线电探空仪资料作为检验层析结果质量的标准。按第3节的方法构建层析方程,层析初值选择为层析时刻前3天的无线电探空仪数据的均值,接下来分别分析松弛因子、迭代终止规则和不同的代数重构算法对层析结果的影响。
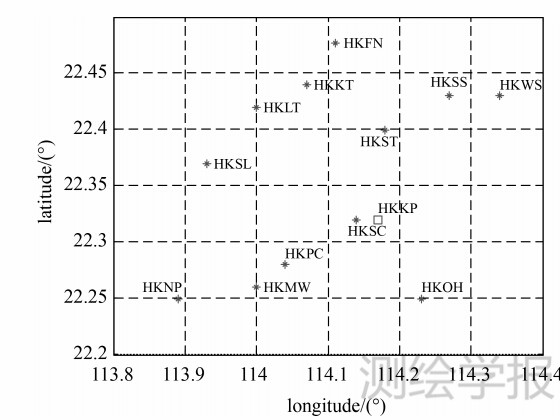 |
| 图 1 SatRef网格划分图 Fig. 1 SatRef schematic meshing |
采用文中5.2节的方法计算出各算法的最优松弛因子(其中Randkaczmarz算法的最优松弛因子由试验得到),并给出各算法松弛因子的有效取值范围、默认值、文献[5,6]提供的经验参考值,如表 1所示。
表 1中, 为A阵最大奇异值的估值;
为A阵最大奇异值的估值; 2为D1/2A最大奇异值的估值;
2为D1/2A最大奇异值的估值; 3为DS1/2A最大奇异值的估值;
3为DS1/2A最大奇异值的估值;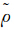 为S-1ATMA谱半径的估值,各参数定义请参考文献[18]。
为S-1ATMA谱半径的估值,各参数定义请参考文献[18]。
首先分析不同松弛因子对解算结果的影响,分别为默认值、文献[5,6]分别给出的经验参考值,以及由5.2节方法计算的最优松弛因子。由于文献[5,6]只给出了 Kaczmarz和SART两种算法的参考松弛因子,故此处仅对这两种算法进行分析(表 2、表 3)。
从表 2、表 3可以看出,在采用同样的迭代初值和终止规则下,不同的松弛因子会导致收敛速度和结果精度不同。在Kaczmarz算法中,系统默认松弛因子最大,收敛最快,但结果精度最低,文献[6]的参考迭代因子最小,结果精度最高,但收敛速度最慢,而黄金分割算法给出的松弛因子精度与文献[6]的参考迭代因子相当,但收敛速度远大于它,综合表现最好;而在SART算法中,4个松弛因子的解算结果精度相当,但最优松弛因子的收敛速度远高于另外3种算法,综合表现也最好。 6.2 迭代终止规则的验证分析
接下来分析不同的迭代终止规则对水汽层析结果的影响。试验选取了最大迭代数(即迭代达到最大迭代数后终止,本试验中设为10000),文献[5]和文献[6]分别给出的参考终止条件,NCP迭代终止条件4种不同迭代终止规则,采用最优松弛因子进行解算(表 4)。
从表 4结果可以看出,采用不同迭代终止规则,水汽层析结果有着较大的差异。在这两种算法中,NCP迭代终止规则的层析结果精度最高;其次为文献[5]提出的参考终止条件,文献[6]与文献[5]精度比较接近,精度最差的是最大迭代数。这说明在代数重构算法中,并非迭代次数越多结果越好,可能到某一点后迭代会发散,导致结果变差,因此选择合理的迭代终止条件很重要,本文提出的NCP终止规则较为理想。 6.3 不同解算方案的结果分析
根据松弛因子和终止规则的不同设计了4种层析方程解算方案,分别为默认松弛因子和最大迭代数(即方案1);最优松弛因子和最大迭代数目(即方案2);默认松弛因子和NCP终止规则(方案3);最优松弛因子和NCP终止规则(方案4),并用8种常见的代数重构算法分别按这4种方案进行解算,将结果整理成表 5。
| 算法 | 方案1 | 方案2 | 方案3 | 方案4 |
| Kaczmarz | 0.5563 | 0.5495 | 0.2714 | 0.2652 |
| Randkaczmarz | 0.6185 | 0.5567 | 0.4318 | 0.2911 |
| Syskaczmarz | 0.5299 | 0.5296 | 0.3127 | 0.2925 |
| SART | 0.5132 | 0.5074 | 0.3202 | 0.3122 |
| Landweber | 0.5025 | 0.5016 | 0.2453 | 0.2387 |
| Cimmino | 0.5032 | 0.4930 | 0.2529 | 0.2330 |
| CAV | 0.4971 | 0.5023 | 0.3123 | 0.2327 |
| DROP | 0.5073 | 0.4948 | 0.2931 | 0.2926 |
由表 5可以看出,对于同样的层析方程,采用不同的方案进行解算,得到的结果精度有较大差异。其中方案1解算结果精度最差,方案4精度最高,后两种方案的结果精度都远高于前两种解算方案。这说明在代数重构算法中,迭代终止规则的确定比松弛因子的选择更为重要。在方案4中,精度最高的为 CAV算法,其次为Cimmino算法。
为了便于更加直观地分析解算结果,这里给出2012年155d 0h京士柏气象站处的水汽层析结果垂直廓线,如图 2所示。
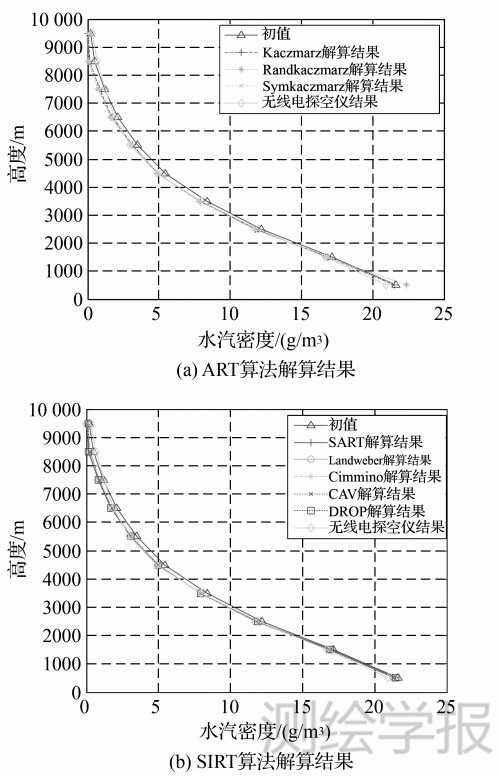 |
| 图 2 采用方案4得到的水汽廓线 Fig. 2 Vapor profile got by strategy 4 |
从图 2可以看出,这8种代数重构算法的结果都能较好地反映出水汽的分布趋势,与无线电探空仪的结果接近,这表明代数重构算法能够较好地实现水汽层析。 7 结 论
本文讨论了代数重构算法在水汽层析应用中的各种问题,包括约束条件,层析方程,松弛因子,终止条件等,并提出了相应解决方案,比较分析了8种常见的代数重构算法。
松弛因子影响着迭代收敛速度和结果精度,在代数重构算法中占有重要地位,本文给出了一种计算最优松弛因子的黄金分割搜索算法,试验表明该算法能以较快的速度收敛到最优结果。迭代终止条件在代数重构算法中也很重要,本文给出了一种NCP迭代终止规则,试验结果表明该终止条件结果稳定可靠,精度较高。试验还证明,迭代终止规则的确定比松弛因子的选择更加重要。在各种层析方程解算方案中,采用文中计算最优松弛因子的算法和NCP迭代终止规则结果精度最高。各种常见的代数重构算法在采用该解算方案时,精度最高的为 CAV算法,其次为Cimmino算法。
| [1] | BEVIS M, BUSINGER S, HERRING T, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801. |
| [2] | DING Jincai. GPS Meteorology and Its Applications[M]. Beijing: Meteorological Press, 2009: 148-161. (丁金才. GPS气象学及其应用[M]. 北京: 气象出版社, 2009: 148-161.) |
| [3] | FLORES A, RUFFINIG G, RIUS A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae, 2000, 18: 223-224. |
| [4] | YU Shengjie, LIU Lintao, LIANG Xinghui. Influence Analysis of Conditions on GPS Water Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 491-496. (于胜杰,柳林涛,梁星辉. 约束条件对GPS水汽层析解算的影响分析[J]. 测绘学报, 2010, 39(5): 491-496.) |
| [5] | BENDER M, DICK G, GE M R, et al. Development of a GNSS Water Vapour Tomography System Using Algebraic Reconstruction Techniques[J]. Advances in Space Research, 2011, 47(10): 1704-1720. |
| [6] | WANG Wei, WANG Jiexian. Ground-based GPS Water Vapor Tomography Based on Algebraic Reconstruction Technique[J]. Journal of Computer Applications, 2011, 31(11): 3149- 3151. (王维,王解先. 基于代数重构技术的对流层水汽层析[J]. 计算机应用, 2011, 31(11): 3149-3151.) |
| [7] | ROHM W. The Ground GNSS Tomography: Unconstrained Approach[J]. Advances in Space Research, 2013, 51(9):501-513. |
| [8] | WEN D B, LIU S Z, TANG P Y. Tomographic Reconstruction of Ionospheric Electron Density Based on Constrained Algebraic Reconstruction Technique[J]. GPS Solution, 2012, 14(4): 375-380. |
| [9] | TROLLER M, GEIGER A, BROCKMANN E, et al. Tomographic Determination of the Spatial Distribution of Water Vapor Using GPS Observations[J]. Advances in Space Research, 2006, 37: 2211-2217. |
| [10] | ROHM W, BOSY J. The Verification of GNSS Tropospheric Tomography Model in a Mountainous Area[J] Advances in Space Research, 2008,47: 1721-1730. |
| [11] | NOTARPIETRO R, CUCCA M, GABELLA M, et al. Tomographic Reconstruction of Wet and Total Refractivity Fields from GNSS Receiver Networks[J]. Advances in Space Research, 2011, 47(1): 898-912. |
| [12] | GRADINARSKY L P, JARLEMARK P. Ground Based GPS Tomography of Water Vapor: Analysis of Simulated and Real Data[J]. Journal of the Meteorological Society of Japan, 2004, 82(18): 551-560. |
| [13] | HIRAHARA K. Local GPS Tropospheric Tomography[J]. Earth Planets and Space, 2000, 52: 935-939. |
| [14] | TROLLER M, GEIGER A, BROCKMANN E, et al. Tomographic Determination of the Spatial Distribution of Water Vapour Using GPS Observations[J]. Advances in Space Research, 2006, 37: 2211-2217. |
| [15] | DENG Z, BENDER M, DICK G, et al. Retrieving Tropospheric Delays from GPS Networks Densified with Single Frequency Receivers[J]. Geophysical Research Letters, 2009, 36(19): 802-806. |
| [16] | HOBIGER T, KONDO T, KOYAMA Y. Constrained Simultaneous Algebraic Reconstruction Technique(C-SART): A New and Simple Algorithm Applied to Ionospheric Tomography[J]. Earth Planets Space, 2008, 60: 727-735. |
| [17] | MING Y. Convergence Analysis of SART: Optimization and Statistics[J]. International Journal of Computer Mathematics, 2013, 90(1): 30-47. |
| [18] | HANSEN P C, SAXILD-HANSE M. AIR Tools: A MATLAB Package of Algebraic Iterative Reconstruction Methods[J]. Journal of Computational and Applied Mathematics, 2012, 236(8): 2167-2178. |
| [19] | HANSEN P C, KILMER M E, KJELDSEN R H. Exploiting Residual Information in the Parameter Choice for Discrete Ill-posed Problems[J]. BIT Numerical Mathematics, 2006, 46: 41-59. |
| [20] | RUST B W, O'LEARY D P. Residual Periodograms for Choosing Regularization Parameters for Ill-posed Problems[J]. Inverse Problems, 2008, 24(3): 34005-34034. |