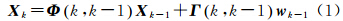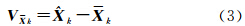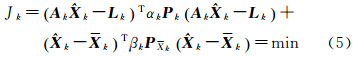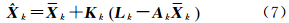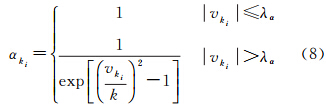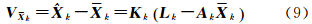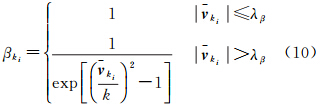2. 国防科技大学航天科学与工程学院，湖南 长沙 410072;
3. 宇航动力学国家重点实验室，陕西 西安 710043
2. School of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410072, China;
3. State Key Lab of Astronautic Dynamics, Xi'an 710043, China
1 引 言
针对误差类别不同而衍生出的自适应滤波、抗差滤波和抗差自适应滤波等不同滤波算法，国内外很多学者进行了广泛研究，并取得了显著成果[1, 2, 3, 4, 5]。对动力学模型信息不精确和观测模型出现误差时，直接利用Kalman算法滤波效果不佳，通常利用自适应滤波对其状态进行估计。自适应滤波是引入一个调节因子来均衡调节动力学模型信息不精确和观测模型误差对滤波估计值的影响[6]。针对状态估计量类型的不同又衍生出多因子和分类因子自适应滤波，其实质都是单因子自适应滤波的推广，因为这些滤波均采用单个因子来均衡调节动力学模型和观测模型误差对估值的影响。分类因子算法主要在处理不同类型(类型不同、数量级也可能不同)的状态量上有优势[7, 8, 9]，多因子其实是将每个因子作为分类因子处理的特例[10]。抗差自适应滤波算法较为均衡地解决了观测模型误差和动力学模型误差对状态参数估计的影响，其主要步骤为先求解状态参数抗差解，然后根据状态参数抗差解求出自适应因子，最后根据自适应因子解算状态参数[5, 6]。
本文基于抗差自适应Kalman滤波算法，引入两个自适应因子分别调节模型误差和观测误差对状态估计的影响，首先分别解算两个自适应因子，然后由两个自适应因子共同解算最终状态参数解[11]。
2 滤波模型 2.1 状态方程推导状态方程
观测方程
式中，Xk为k时刻的状态量向量；Φ(k,k-1)为状态转移矩阵；Γ(k,k-1)为系统噪声矩阵；wk-1为系统噪声向量；Lk为k时刻的观测向量；Ak为观测矩阵；ek为观测噪声向量。
状态向量预报误差方程
由于状态向量预报xk=Φ(k,k-1)
k-1，其中，Φ(k,k-1)含有动力学积分过程，Vxk反映动力学模型误差。
观测向量误差方程
式中，Lk观测向量信息；Vk反映观测值的误差。 式(5)对
k求导，并令其导数为0，得
由矩阵恒等变换可得
式中，Kk=(AkTαkPkAk+βkPxk)-1AkTαkPk为增益矩阵；Pk为状态估计向量的权矩阵；Pxk为状态预测向量的权矩阵；αk为时刻k观测自适应因子；βk为k时刻动力学模型信息的自适应因子，即对动力学模型的认可度。 2.2 自适应因子选取
动力学模型信息自适应因子βk和观测模型自适应因子αk可参照抗差估计方法中指数型两段法对其进行计算[5]，其中
2.2.1 αki自适应因子选取[19, 20, 21, 22]
式(4)反映了观测残差，现对其第i项分量Vki进行标准化处理，即vki=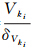
，δVki是Vki的均方差[6]，取λα为阈值，其范围是λα∈[1.0,3.0]
式(3)反映了模型信息的精确性，将式(7)代入式(3)，则
第1种方案：取式(9)为状态的预测残差。
第2种方案：直接取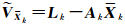
为状态的预测残差，即简化的状态预测残差。
对状态预测残差第i项分量
进行标准化处理，即
,δvki是的均方差[6]，取λβ为阈值，其范围是λβ∈[1.0,3.0]
设一辆汽车在公路上行驶，在车上安装两个路程传感器A和B，传感器A的路程测量精度为5 m(1σ)；传感器B的路程测量精度1 m(1σ)；t表示时间，单位为秒；S表示位移，单位为m；v表示速度，单位为m/s；a表示加速度，单位为m/s2。汽车两种工作模式如下：
(1) 在t∈ [0,1500]期间，汽车以v=20 m/s匀速直线运动。
(2) 在t∈ [0,500) 期间，汽车以v=20 m/s的速度匀速直线运动，汽车中途在t∈ 500,550以a=1 m/s2的加速度作匀加速运动，在t∈[550,1500)期间，汽车以v=20 m/s的速度匀速直线运动。其中工作模式(2)中汽车在t∈[500,550)作匀加速运动是模拟动力学模型不准对估计的影响。
 |
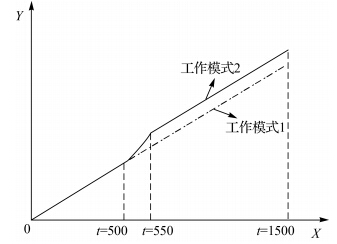| 图 1 汽车工作模式图Fig. 1 The figure of the work mode of the car |
方案1：用标准Kalman滤波算法估计汽车位移S，简称SKF。
方案2：将预测残差进行简化，即=Lk-Akxk，采用双自适应因子滤波算法估计位移S，简称SDAF。
方案3：用抗差自适应Kalman滤波算法[1]估计位移S，简称RAF。
方案4：采用非简化预测残差的双自适应子滤波算法估计位移S，简称DAF。
对上述汽车工作模式进行建模，设汽车状态位置矢量S，速度矢量v，t0为初始时刻，S0为t0时刻的位移，则汽车的状态量设为X=[S v]T，CV模型如下
S=S0+vt-t0
则状态转移矩阵为
状态方程为Xk=Φ(k,k-1)Xk-1+Wk，其中Wk为模型误差。
观测方程Yk=Axk+Vk，其中A=[1 0]，Vk为测量误差。
时间更新如下
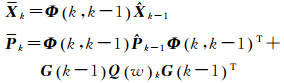
测量更新如下
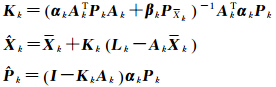
方案2、方案3和方案4中自适应因子的比较门限值采用相同设置，即观测自适应因子λα=2.5，动力学模型信息自适应因子λβ=1.5。
算例1：汽车整个过程处在工作模式1下。此算例主要用于验证动力学模型信息和观测模型误差均正常时，双自适应因子滤波算法在通常的情况下是否与标准Kalman滤波一致，4种算法的性能如图 2-图 5所示。
 |
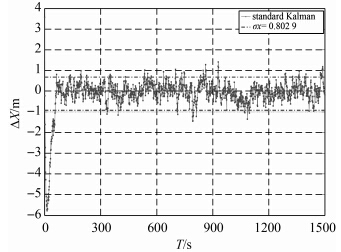| 图 2 标准Kalman估计误差Fig. 2 The estimation error of the standard Kalman |
 |
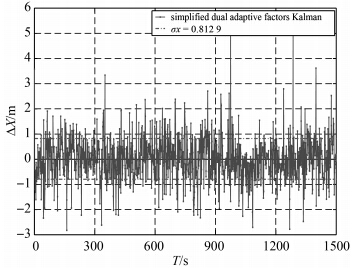| 图 3 SDF估计误差Fig. 3 The estimation error of SDF |
 |
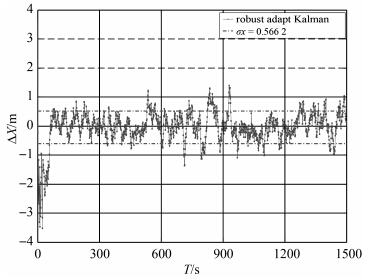| 图 4 RAF估计误差Fig. 4 The estimation error of RAF |
 |
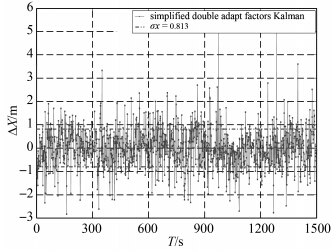
| 图 5 DAF估计误差Fig. 5 The estimation error of DAF |
算例2：汽车工作在模式1下，每300 s给传感器A加入300 m粗差。此算例主要是验证观测模型发生异常、动力学模型信息正确时，双因子自适应滤波算法是否能够抵御观测粗差对状态估计的影响，4种算法的性能如图 6-图 9所示。
 |
| 图 6 标准Kalman估计误差Fig. 6 The estimation error of standard Kalman |
 |
| 图 7 SDF估计误差Fig. 7 The estimation error of SDF |
 |
| 图 8 RAF估计误差Fig. 8 The estimation error of RAF |
 |
| 图 9 DAF估计误差Fig. 9 The estimation error of DAF |
算例3：汽车在模式2下工作，中间有50 s的加速运动，并且每300 s对传感器A加入300 m的粗差。此算例用于验证模型信息和观测均存在异常时，双因子自适应滤波算法是否能够抵御两种粗差对状态估计的影响，能否达到抗差自适应算法的性能，4种算法的性能如图 10-图 13所示。
 |
| 图 10 标准Kalman估计误差Fig. 10 The estimation error of standard Kalman |
 |
| 图 11 SDF估计误差Fig. 11 The estimation error of SDF |
 |
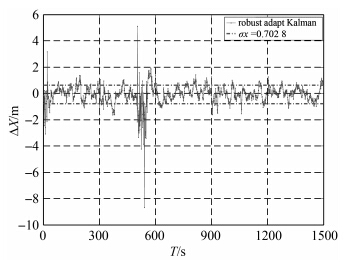| 图 12 RAF估计误差Fig. 12 The estimation error of RAF |
 |
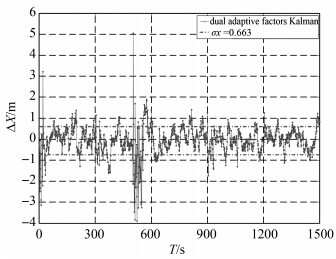| 图 13 DAF估计误差Fig. 13 The estimation error of DAF |
由上面的仿真结果可以得出以下结论：
(1) 标准Kalman滤波算法易受到误差的扰动出现较大波动。尤其是当动力学模型信息不精确时，标准Kalman滤波则会出现较大波动，见图 2、图 6和图 10。
(2) 简化残差的双自适应因子滤波算法性能比较稳定，但是由于简化残差较大，对误差的变化较为敏感，因此简化残差的双自适应因子滤波算法表现出较为频繁的波动特性，见图 3、图 7和图 11。
(3) 抗差自适应算法和双自适应因子算法性能较为稳定，不仅能抑制观测粗差对估值的影响，而且能够较好地削弱动力学模型不精确对估值的影响，见图 4、图 5、图 8、图 9、图 12和图 13。由表 1可以看出，单就RMS来说，双自适应因子滤波算法的RMS要略低于抗差自适应滤波算法。
| m | ||||
| RMS | SKF | SDAF | RAF | DAF |
| 算例1 | 0.802 9 | 0.812 9 | 0.566 2 | 0.560 4 |
| 算例 2 | 0.933 | 0.813 | 0.584 2 | 0.580 7 |
| 算例 3 | 11.37 | 0.877 3 | 0.702 8 | 0.663 |
本文提出了双自适应因子滤波算法，通过两个自适应因子分别调节动力学模型误差和观测模型误差对滤波估值的影响，理论上推导了双自适应因子算法的滤波模型，并进行了建模和仿真验证，结果表明该算法具有同时抵制观测异常和动力学模型异常影响的能力。但该算法适用于动力学模型短时间出现小范围异常误差，若动力学模型长时间不准确或者动力学模型异常误差过大，则可能导致滤波发散。
| [1] | ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J].Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115-120.(周江文. 经典误差理论和抗差估计[J]. 测绘学报,1989,18(2):115-120.) |
| [2] | YANG Yuanxi. Adaptively Robust Least Squares Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 205-211.(杨元喜.自适应抗差最小二乘估计[J]. 测绘学报,1996,25(3):205-211.) |
| [3] | YANG Yuanxi. Robust Estimation for Dependent Observations[J].Manuscripta Geodaetica,1994, 19: 10-17. |
| [4] | YANG Yuanxi, HE Haibo, XU Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 293-298.(杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报,2001,30(4): 293-298.) |
| [5] | YANG Yuanxi, REN Xia, XU Yan. Major Progress in Adaptive Robust Filtering Theory and Application[J]. Navigation and Positioning, 2013,1:9-15.(杨元喜, 任夏, 许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报,2013,1:9-15.) |
| [6] | YANG Yuanxi. Adaptive Navigation and Kinematic Positioning [M]. Beijing: Surveying and Mapping Press,2006.(杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006.) |
| [7] | CUI Xianqiang, YANG Yuanxi. Adaptively Robust Filtering with Classified Adaptive Factors[J]. Progress in Nature Science, 2006, 16(8): 846-851. |
| [8] | HUANG Guanwen, YANG Yuanxi, ZHANG Qin. Estimate and Predict Satellite Clock Error Using Adaptively Robust Sequential Adjustment with Classified Adaptive Factors Based on Opening Windows[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):15-21.(黄观文, 杨元喜, 张勤. 开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J]. 测绘学报,2011, 40(1): 15-21.) |
| [9] | ZHANG Liping, ZENG Anmin. Determination of Coordinate Transformation Parameters by Adaptively Adjustment Method with Classified Adaptive Factors [J]. Geodesy and Geodynamics, 2008,28(2):110-114.(张丽萍, 曾安敏. 用分类因子自适应序贯平差法确定坐标转换参数[J]. 大地测量与地球动力学,2008,28 (2): 110-114.) |
| [10] | YANG Yuanxi, CUI Xianqiang. Adaptively Robust Filter with Multi Adaptive Factors[J]. Survey Review, 2008, 40(309): 260-270. |
| [11] | SU Tianxiang. The Rresearch of Autonomous Orbit Determination of Navigation Constellation with Distribution Algorithm Based on Ground-based Anchor [D]. Changsha: National University of Defense Technology,2012.(苏天祥. 基于锚固站的导航星座自主定轨技术研究[D]. 长沙: 国防科技大学, 2012.) |
| [12] | LIU Jun, XIA Zhixun. Dynamics System Identification and Modeling[M].Changsha: Press of National University of Defense Technology,2007.(刘君, 夏智勋. 动力学系统辨识与建模[M]. 长沙: 国防科技大学出版社, 2007.) |
| [13] | HUBER. Robust Statistics[M]. New York: John Wiley, 1981. |
| [14] | WU Fumei, YANG Yuanxi. An Extended Adaptive Kalman Filtering in Tight Coupled GPS/INS Integration[J].Survey Review,2010,40(316):146-154. |
| [15] | YANG Yuanxi, GAO Weiguang, Zhang Shuangcheng. Robust Kalman Filtering with Constraints: a Case Study for Integrated Navigation[J].Journal of Geodesy, 2010,84:373-381. |
| [16] | YANG Yuanxi. Properties of Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 189-192.(杨元喜. 动态定位自适应滤波解的性质[J]. 测绘学报,2003,32(3): 189-192.) |
| [17] | LI Chong, HUANG Guanwen, TAN Li, et al. Adaptive Robust Kalman Filtering Applied in GPS Precise Point Positioning[J]. Science of Surveying and Mapping, 2011, 36(4): 22-24.(李冲, 黄观文, 谭理等. 抗差自适应卡尔曼滤波在GPS精密单点定位中的应用[J] 测绘科学,2011, 36(4): 22-24.) |
| [18] | WU Fumei, YANG Yuanxi. A New Two Step Adaptive Robust Kalman Filtering in GPS/INS Integrated Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5):522-527.(吴富梅, 杨元喜. 一种两步自适应抗差Kalman滤波在GPS/INS组合导航中的应用[J]. 测绘学报, 2010,39 (5): 522-527.) |
| [19] | GAO Weiguang, YANG Yuanxi, ZHANG Shuangcheng. Adaptive Robust Kalman Flitering Based on the Current Statistical Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1):15-19.(高为广, 杨元喜, 张双成. 基于当前加速度模型的抗差自适应KALMAN滤波[J]. 测绘学报,2006, 35(1):15-19.) |
| [20] | YANG Yuanxi, GAO Weiguang. Comparison of Two Fading Filtering and Adaptively Robust Filter[J]. Geometrics and Information Science of Wuhan University,2006, 31(11): 980-982.(杨元喜, 高为广. 两种渐消滤波与自适应抗差滤波的综合比较分析[J].武汉大学学报:信息科学版,2006, 31(11): 980-982.) |
| [21] | GAO Weiguang, ZHANG Shuangcheng, WANG Fei, et al. Adaptive Robust Kalman Filtering Algorithm in GPS Navigation[J]. Science of Surveying and Mapping,2005,30(2):98-100.(高为广, 张双成, 王飞,等. GPS导航中的抗差自适应Kalman滤波算法[J]. 测绘科学,2005,30(2):98-100.) |