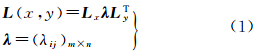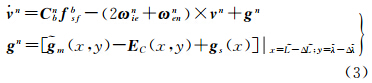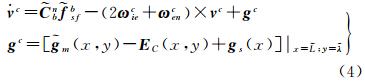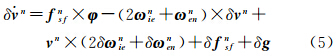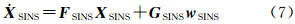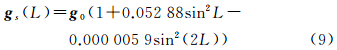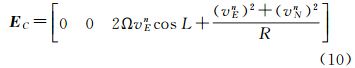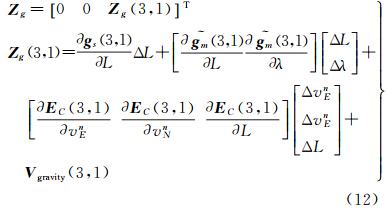2. 中国人民解放军96124部队,吉林 通化 134000
2. Unit 96124, Tonghua 134000, China
1 引 言
现有海洋重力异常场分辨率已经达到2′×2′,进一步插值精细化处理可达1′×1′,海洋重力仪的测量精度达到1 mGal(1 Gal=10-2 m/s2),这给高精度的重力辅助导航提供了可能性[1, 2, 3, 4]。自主水下航行器重力辅助惯性导航作为一种利用地球重力场特征信息结合匹配算法对惯性导航系统位置信息进行初次估计,而后采用导航数学模型方程结合一定的滤波算法对惯性导航系统位置信息进行进一步精化修正的新技术,近年来无论是理论还是实践应用都得到了快速的发展。目前关于重力匹配算法的文献较多,研究也比较透彻,按照匹配算法设计原理可分为序列相关匹配方法和递推滤波方法两种,序列相关匹配方法主要分为最近等值线迭代算法(ICCP)和相关极值分析算法两大类[5, 6, 7, 8, 9, 10, 11]。文献[7]给出了一种基于平均平方差最小准则构造差分降权相关目标函数模型的相关极值分析算法,有效修正了重力辅助导航的误差。文献[9]在0.2′×0.2′重力辅助异常数据库的基础上,提出将匹配位置误差作为观测量,用卡尔曼滤波对惯性导航系统进行最优估计的最近等值线迭代算法(ICCP)匹配算法。重力异常图一般是以规则格网形式预先存储在匹配计算机中,如何获取高精度、高分辨率的重力异常图是进行准确匹配的关键所在。高斯样条函数具有局部支撑的良好特性,用其作为样条基函数对计算区域重力异常进行二维整体逼近,能在保证重力异常局部特性不失真的前提下获取计算区域重力异常的统一解析式等优点。文献[12]给出了一种基于快速傅里叶技术建立连续局部重力场的重力辅助导航算法,定位误差小于350 m。文献[13]提出了一种基于斐波那契数列利用二维高斯样条函数逼近局部重力异常场的方法,得到高精度逼近局部离散格网数据的局部重力异常场连续解析模型,连续解析模型逼近绝对误差均值达到0.000 69 mGal。文献[15]给出了一种基于余弦变换的Parker正演重力梯度方法。
自主水下航行器惯性导航系统中加速度计无法区分运动加速度和重力加速度,需要通过其他手段将比力中的重力加速度扣除,称为重力补偿。如文献[5, 8, 9, 10, 12]所述,目前传统自主水下航行器重力辅助导航系统模型的构建过程中,认为比力中的重力加速度为标准重力模型,未考虑重力异常扰动矢量、标准重力模型误差(标准重力模型误差由测量位置维度误差解算引起)和厄特弗斯修正计算值3类误差影响(本文所述的传统模型就是指不考虑3类误差影响,认为比力中的重力加速度为标准重力模型)。这些误差都将引起导航误差,在惯性元件精度不高的系统中,惯性元件带来的系统误差较大,相比之下,正常重力模型足够精确,这些系统误差可以忽略。但在精度要求较高的场合(重力辅助导航中陀螺仪零偏小于0.001 deg/h,加速度计零偏小于0.01 mg的情况下),尤其是随着惯性元件精度的不断提高,其带来的系统误差与上述3类误差带来的系统误差处在同一个量级,甚至前者可能低于后者,系统误差不能被忽略,有必要采用精度更高的系统状态方程模型对正常重力矢量进行补偿,应在初次重力匹配算法计算经纬度结果的基础上,对标准重力模型误差、重力扰动矢量和厄特弗斯修正计算值进行补偿,而后再进行整个系统的导航滤波计算,目前并未有这方面的研究[15, 16, 17, 18, 19, 20]。因此,本文基于二维高斯样条局部重力异常场提出了一种考虑重力扰动矢量、标准重力模型误差、厄特弗斯修正计算值的精化自主水下航行器重力辅助导航模型构建算法。
2 高斯基函数插值高斯样条基函数G(x)=e(-x2/a2),a为局部支撑参数,设局部重力异常图等分格网点为{(xi,yj,zi,j)|i=1,2,…,m;j=1,2,…,n},Δx、Δy为格网点分辨率。这样符合上述x、y平面的二维高斯基函数可写成矩阵形式
式中,Lx=[Gx((x-x1)/Δx)Gx((x-x2)/Δx…Gx((x-xm)/Δx)];Ly=[Gy((y-y1)/Δy)Gy((y-y2)/Δy…Gx((y-yn)/Δy)];简记为Lx=Inte{Gx((x-xi)/Δx)},Ly=Inte{Gy((y-yi)/Δy)}根据插值条件
{L(xi,yi)=f(xi,yi) i=1,2,…,m;j=1,2,…,n},
将矩阵组合,则有如下线性方程成立式中,Z=(Zij)m×n;Zij=L(xi,yi);
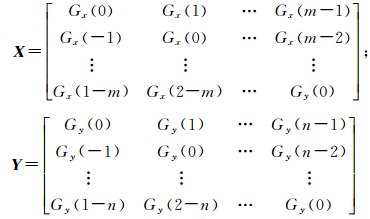
可见,高斯基插值函数存在两个重要参数需要确定:①插值系数矩阵λ;②局部支撑参数a。无论是一维高斯基函数还是二维高斯基函数,如果X、Y均为非奇异矩阵,则式(2)有唯一解,对X、Y矩阵求逆,解方程即得到插值系数矩阵,将插值系数矩阵λ代入式(1)便得到该局部重力异常基准图二维高斯基函数逼近解析式。研究证明,局部支撑参数a的取值对高斯基函数逼近效果影响很大,a过大或过小都将导致很大的逼近误差。当a过小时,由于局部支撑区间很小,使得插值曲线刚度小,容易出现锯齿状;当a过大时,由于局部支撑区间很大,插值曲线刚度大,插值曲线过于平滑甚至使插值解析式在已知点的插值误差很大,所以a太大或太小均会失去插值的意义。因此有必要对参数a进行寻优,结合插值模型精度评估方法,解算参数a的最优值。文献[13]中的二维高斯函数插值局部寻优方法对a进行寻优,建立局部连续重力场。
3 基于高斯插值的精化算法 3.1 速度误差方程取地理坐标系n为导航坐标系;b表示载体坐标系;Cbn表示由载体坐标系向导航坐标系转换。假设姿态误差角φ是小角度,在考虑因重力扰动矢量、标准重力模型误差和厄特弗斯修正计算值的情况下,重力辅助导航速度误差方程的具体推导叙述如下:
在不考虑任何误差的情况下,认为根据导航仪表所示载体位置为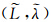 ,经过重力匹配算法初次计算得到的实际位置为
,经过重力匹配算法初次计算得到的实际位置为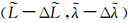 ;根据比力方程,速度理想方程由下述方程(3)给出
;根据比力方程,速度理想方程由下述方程(3)给出
考虑各种误差的情况下,实际速度计算值应由下述方程确定
式中,vc=vn+δvn;ωcie=ωnie+δωnie;ωcen=ωnen+δωnen;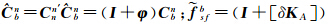 (I+[δA])+
(I+[δA])+ b;
b;
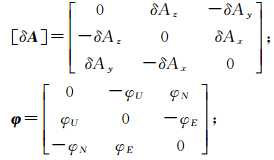
式(4)与式(3)相减,略去二阶小量可得线性近似的捷联惯导误差方程为
式中,δg=[ m(x,y)-EC(x,y)+
m(x,y)-EC(x,y)+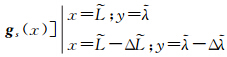 ;δfnsf=Cnb{(δA+[δKA])fbsf+
;δfnsf=Cnb{(δA+[δKA])fbsf+ b};m(x,y)为前述高斯插值计算得到的连续重力异常场表达式;gs(x)、EC(x,y)分别为后文叙述的标准重力模型表达式和厄特弗斯修正计算值。
3.2 状态方程
b};m(x,y)为前述高斯插值计算得到的连续重力异常场表达式;gs(x)、EC(x,y)分别为后文叙述的标准重力模型表达式和厄特弗斯修正计算值。
3.2 状态方程
除速度误差方程外,本文所提导航系统的其他误差方程与其他文献中的误差方程相同[20, 21, 22, 23],定义SINS的状态变量如下,共15维状态矢量XSINS=[φT δvnT δpT εbT  bT]T,其中,φT=[φE φN φU];δvnT =[δvnEδvnNδvnU];δpT=[L λ h]分别为惯导系统姿态角、速度、位置误差。将加速度计误差模型近似为随机常值零偏加白噪声,陀螺误差模型近似为随机常值漂移加白噪声,这样陀螺仪漂移误差εbT、加速度偏移误差ΔbT方程见式(6)
bT]T,其中,φT=[φE φN φU];δvnT =[δvnEδvnNδvnU];δpT=[L λ h]分别为惯导系统姿态角、速度、位置误差。将加速度计误差模型近似为随机常值零偏加白噪声,陀螺误差模型近似为随机常值漂移加白噪声,这样陀螺仪漂移误差εbT、加速度偏移误差ΔbT方程见式(6)
于是可得到基于高斯插值的导航状态方程
式中,系统噪声wSINS=[wgx wgyw gz wax way waz]T为6维系统干扰白噪声;系统噪声分配矩阵为GSINS是15×6矩阵;状态矩阵FSINS是15×15矩阵。 3.3 量测方程本文系统量测值取重力仪量测重力与惯导指示位置对应连续场重力图重力之差。设定此时系统的量测方程Zg可由式(8)计算得出
式中,g0=[0 0 978 049]T,单位为mm/s2。
设导航仪表所示载体位置为(L+ΔL,λ+Δλ);对应的实际位置为(L,λ);m(L+ΔL,λ+Δλ)为在重力图上根据载体测量位置(L+ΔL,λ+Δλ)读出的重力异常值; s(L+ΔL)为根据载体纬度测量位置信息L+ΔL利用标准重力公式(9)计算得到的重力值;
s(L+ΔL)为根据载体纬度测量位置信息L+ΔL利用标准重力公式(9)计算得到的重力值; (L,λ)为重力传感器输出的实际重力值;EC(L+ΔL,λ+Δλ)为利用式(10)计算得到的厄特弗斯修正计算值。
(L,λ)为重力传感器输出的实际重力值;EC(L+ΔL,λ+Δλ)为利用式(10)计算得到的厄特弗斯修正计算值。
厄特弗斯修正计算值的计算公式为[1]
式中,vnE和vnN为载体的东向和北向速度;L为载体当地的大地纬度;Ω=7.292 115 67×10-5rad/s表示地球自转角速率。由于绘制成的重力图值等于实际重力测量值经过厄特弗斯修正而后减去标准重力值,所以对于实际位置点(L,λ),有[3]
则
 (L,λ)=
(L,λ)= m(L,λ)-EC(L,λ)+gs(L),将其代入方程式(8),经线性化处理后可得系统量测方程
式中,Vgravity为重力传感器噪声、重力异常图制作噪声和线性化误差总和,在实际计算中,重力异常梯度
m(L,λ)-EC(L,λ)+gs(L),将其代入方程式(8),经线性化处理后可得系统量测方程
式中,Vgravity为重力传感器噪声、重力异常图制作噪声和线性化误差总和,在实际计算中,重力异常梯度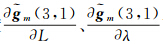 可以采用9点拟合、全平面拟合等方法计算。
可以采用9点拟合、全平面拟合等方法计算。测量矩阵为
式中,Zgline为式(8)计算得到的重力测量误差值;Hline为1×15维矩阵,在矩阵Hline中,Hline(1,4)=
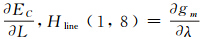 ;其余元素均为0。Vgravityline为重力传感器的噪声、重力异常图制作噪声和线形化误差总和。
4 仿真试验与分析
;其余元素均为0。Vgravityline为重力传感器的噪声、重力异常图制作噪声和线形化误差总和。
4 仿真试验与分析本文采用第二炮兵工程大学惯性导航实验室基于Windows 2000操作系统、Matlab 7.0软件自行开发研制的惯性导航轨迹生成软件,使用代码为real-trace和inertial navigation-trace的两个函数调用相应的子库函数,仿真生成需要的真实航迹和惯导指示航迹[23]。而重力异常数据使用渤海地区经度范围118°E-119°E,纬度范围37°N-38°N的真实数据,该重力异常场的三维图如图 1所示。重力图分辨率为1′×1′,重力仪的实时量测数据是利用真实航迹在重力数据库中的采样值叠加0.4 mGal的随机量测噪声获取,陀螺常值漂移取0.01°/h,随机噪声漂移为0.01°/h,加速度计随机常值零偏1×10-4 g,随机噪声漂移为1×10-5 g。初始状态:速度10 m/s、经度118.02°E、纬度37.24°N、惯导测量经纬度误差0.02°、对准水平姿态误差角2′、对准航向误差角10′。运动载体保持俯仰角和横滚角10°、航向角30°的姿态,0.005 m/s2加速度每隔10 min加速一次,3 min采样匹配滤波一次,行进了70 min,得到24个测量点[23]。在捷联惯导的情况下进行仿真,对比分析了ICCP算法初次估计解算,局部连续场情况下(文献[13]进行高斯插值,最优局部支撑参数abest=1.535 7)传统重力辅助导航模型(认为比力中的重力加速度为标准重力模型值,未考虑重力异常扰动矢量、标准重力模型值误差和厄特弗斯修正计算值3类误差影响建立重力辅助导航系统模型)和本文的基于高斯插值的精化重力辅助导航模型构建算法的效果(分别称其为tradition-ICCP和Gauss-compensation-ICCP算法,简记为TRAI和GACOI算法)。
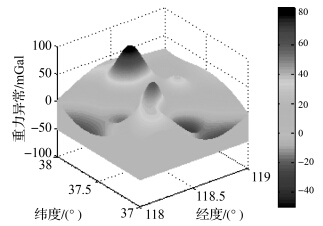 |
| 图 1 重力异常场三维图Fig. 1 3D map of gravity anomaly field |
图 2(a)-(c)分别为TRAI和GACOI算法导航经、纬度位置误差;航向、俯仰、横滚姿态误差角;东、北、天向速度误差分布图。如图 2所示;TRAI算法导航位置误差在125~330 m、平均为210 m,水平姿态误差在0.2′~0.75′、平均为0.50′,航向姿态误差在4′~9′、平均误差为7.5′,速度误差在0.027~0.085 m/s、平均误差为0.045 m/s。GACOI算法导航能够保持在100~200 m、平均110 m的位置误差,0.01′~0.25′、平均0.18′的水平姿态误差,2′~6′、平均2.5′的航向姿态误差,0.002~0.05 m/s、平均0.016 m/s的速度误差。可见GACOI算法将传统重力辅助惯性导航算法的位置导航精度提高了1倍左右,姿态角导航精度、速度导航精度提高了1~2倍。新算法由于引入了先进的局部支撑模型参数确定方法,同时考虑重力扰动矢量、标准重力模型误差、厄特弗斯修正计算值,提高了导航精度,达到了近乎高精度导航的水平。
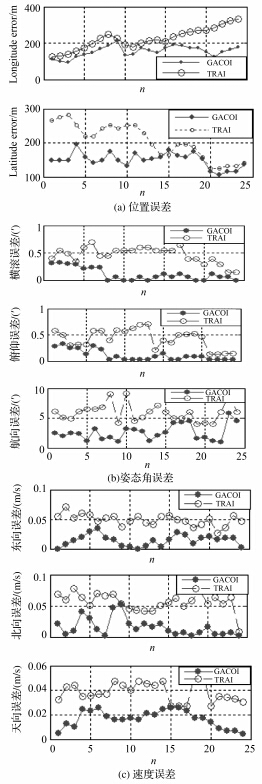 |
| 图 2 导航仿真误差分析图Fig. 2 The analysis of navigation simulation errors |
本文首先对高斯样条优化插值以及所涉及的局部支撑参数求解问题进行研究探讨,给出了局部连续重力异常场的构建方法,而后基于此给出了考虑重力扰动矢量误差、标准重力值误差、厄特弗斯修正计算误差的高斯插值精化导航算法,最终提高了重力辅助导航系统的导航精度,实现了精化导航计算的目的。本文算法可以为重力辅助惯性导航算法的实践化提供一定参考,然而在重力辅助导航系统观测量为非线性的情况下,如何基于局部连续重力异常场进行相应的重力辅助导航非线性滤波算法设计还有待进一步研究。
| [1] | LOWREY J A, SHELLENBARGER J C. Passive Navigation Using Inertial Navigation Sensors and Maps[J]. Naval Engineers Journal, 1997, 109(3): 245-249. |
| [2] | BISHOP G C. Gravitational Field Maps and Navigational Errors [J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 726-737. |
| [3] | RICE H, KELMENSON S, MENDELSOHN L. Geophysical Navigation Technologies and Applications[C]//Proceedings of Position Location and Navigation Symposium.[S.l.]:IEEE, 2004: 618-624. |
| [4] | KIM A, GOLNARAGHI M F. Initial Calibration of an Inertial Measurement Unit Using an Optical Position Tracking System[C]//Proceedings of Position Location and Navigation Symposium.[S.l.]:IEEE, 2004: 96-101. |
| [5] | WANG Hubiao, WANG Yong, FANG Jian. Simulation Research on a Minimum Root-mean-square Error Rotation-fitting Algorithm for Gravity Matching Navigation[J]. Science China: Earth Sciences. 2012,42(7):1055-1062.(王虎彪, 王勇, 方剑. "最小均方误差旋转拟合法"重力辅助导航仿真研究[J]. 中国科学:地球科学,2012,42(7):1055-1062.) |
| [6] | YAN Li, CUI Chenfeng, WU Hualing. A Gravity Matching Algorithm Based on TERCOM[J]. Geomatics and Information Science of Wuhan University,2009,34(3):261-264.(闫利,崔晨风,吴华玲. 基于TERCOM算法的重力匹配[J].武汉大学学报:信息科学版,2009,34(3):261-264.) |
| [7] | LI Shanshan, WU Xiaoping, MA Biao. Correlative Extremum Matching Algorithm Using Underwater Gravity Anomalies[J]. Acta Geodaetica et Cartographica Sinica,2011,40(4):464- 470.(李姗姗,吴晓平,马彪. 水下重力异常相关极值匹配算法[J]. 测绘学报,2011,40(4):464-470.) |
| [8] | CHEN Yi, XIU Chunbuo, LUO Jing. The Simulation of ICCP Algorithm in the Gravity Aided Navigation[C]//Proceedings of Second International Conference on Intelligent Networks and Intelligent Systems.Tianjin:IEEE,2009,25,62-65. |
| [9] | WANG Zhigang, BIAN Shaofeng. ICCP Algorithm for Gravity Aided Inertial Navigation [J]. Acta Geodaetica et Cartographica Sinica, 2008,37(2):147-151.(王志刚, 边少锋. 基于ICCP算法的重力辅助惯性导航[J].测绘学报, 2008,37(2):147-151.) |
| [10] | YUAN G, ZHANG H W, YUAN K F. A Combinational Underwater Aided Navigation Algorithm Based on TERCOM/ICCP and Kalman Filter[J].IEEE Journal of Sciences and Optimization,2011,23(1),952-955. |
| [11] | SUN Feng, WANG Wenjing, GAO Wei. Contour Matching Algorithm for Passive Gravity Navigation[J]. Chinese Journal of Scientific Instrument, 2009,30(4):817-823.(孙枫, 王文晶, 高伟. 用于无源重力导航的等值线匹配算法[J]. 仪器仪表学报,2009,30(4):817-823.) |
| [12] | WANG Zhigang, BIAN Shaofeng, XIAO Shenghong. Underwater Gravity Aided Inertial Navigation Based on Local Gravity Field Model [J]. Acta Geodaetica et Cartographica Sinica, 2009,38(5):408-414.(王志刚,边少锋,肖胜红. 基于局部地球重力场模型的水下重力辅助惯性导航[J].测绘学报, 2009,38(5):408-414.) |
| [13] | TONG Yude, BIAN Shaofeng, JIANG Dongfang. The Reconstruction of Local Gravity Anomaly Field Based on Spline Function[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(5):756-760.(童余德,边少锋,蒋东方.基于高斯样条函数的局部重力异常场解析重构[J].测绘学报, 2012,41(5):756-760.) |
| [14] | LIU Qiang, XU Xiaosu. Study on Sea-bottom Topographic Data Griding Methods [J]. Ship Electronic Engineering, 2013,33(5):59-64.(刘强,徐晓苏. 海底地形数据网格化方法研究[J]. 舰船电子工程,2013,33(5):59-64.) |
| [15] | LIU Fanming, ZHANG Yingfa, JING Xin, et al. Gravity Gradient Parker's Forward Method and Application Using Cosine Transform [J]. Acta Geodaetica et Cartographica Sinica, 2013,42(2):177-190.(刘繁明,张迎发,荆心,等. 利用余弦变换的重力梯度Parker正演方法及其应用[J].测绘学报, 2013,42(2):177-190.) |
| [16] | GUO Qiuying, XU Zunyi.Study on Error Correction of Gravity Surveying in Underwater Gravity Aided Navigation System[J].Progress in Geophysica 2012, 27(3):1274-1279.(郭秋英,徐遵义. 水下重力辅助导航中重力测量误差改正研究[J].地球物理学进展, 2012,27(3):1274-1279.) |
| [17] | LI Shengquan, OUYANG Yongzhong, CHANG Guobin. Compensation Technology of Gravity Disturbance Vector in Inertial Navigation System[J]. Journal of Chinese Inertial Technology, 2012, 20(4),410-414.(李胜全,欧阳永忠,常国宾. 惯性导航系统重力扰动矢量补偿技术[J]. 中国惯性技术学报,2012, 20(4),410-414.) |
| [18] | SUN Zhongmiao, ZHAI Zhenhe, XIAO Yun, et al. Systematic Error Compensation for Airborne Gravimetry[J], 2013, 56(1), 47-54. (孙中苗,翟振和,肖云,等. 航空重力测量的系统误差补偿 [J]. 地球物理学报, 2013, 56(1), 47-54.) |
| [19] | LUO Di, LIU Zhan, ZHANG Wang, et al. Several Issues in Gravity Correction[J]. Chinese Journal of Scientific Instrument, 2013,28(1):111-121.(骆迪,刘展,张旺,等. 重力校正中存在的若干问题[J].地球物理学进展, 2013,28(1):111-121.) |
| [20] | WANG Yandong, HU Huafeng,YANG Shaoshuai, et al. Application of Gravity Gradient Data in Navigation System. [J]. Electronics Optics and Control,2013,20(11):11-16.(王艳东,胡华峰,杨少帅,等. 重力梯度数据在导航系统中的应用[J]. 电光与控制,2013,20(11):11-16.) |
| [21] | LUO Qing, GAO Xiaoying,WANG Lina. On The INS /GIS Integrated Navigation Algorithm. [J]. Aerospace Control and Application,2013,39(1):40-44.(罗婷,高晓颖,王丽娜. INS/GIS组合导航方法研究[J]. 空间控制技术与应用,2013,39(1):40-44.) |
| [22] | WANG Fenglin, WEN Xiulan, LIN Jian, et al. Federated Kaman Filter for Rate Azimuth Inertial Platform/Log/Gravity Matching Integrated Navigation System. [J]. Aerospace Control and Application,2009,39(2):49-55.(汪凤林,温秀兰,林健, 等. 联邦滤波在RAPINS /计程仪/重力匹配组合导航系统中的应用[J]. 东南大学学报:自然科学版,2009,39(2):49-55.) |
| [23] | YAN Gongmin. The Study of Vehicle Position and Azimuth Determining System [D].XI'an:Northwestern Polytechnical University,2006.(严恭敏.车载自主定位定向系统研究[D].西安:西北工业大学,2006.) |