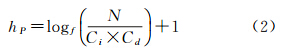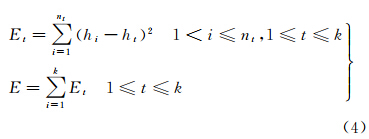1 引 言
随着空间数据采集技术的发展,逐项(one by one,OBO)装载、插入待索引对象的空间索引难以满足海量、动态空间数据的查询管理需求[1]。支持批量操作的空间索引成为当前的研究热点之一[2]。
从空间索引的构建方式来讲,支持批量操作的索引主要包括自上(根节点)而下(叶子节点)、自下而上两种方式。自上而下的批量处理方式中比较典型的是TGS R树[3]、OMT[4]、Merging R树(small tree large tree,STLT)[5]、GBI[6]、SCB[7]。TGS R树对数据进行递归二路划分,自上而下构建索引树。OMT采用最小化节点重叠度的空间划分方法将空间进行递归划分,自上而下递归构建索引树。Merging R树首先根据待索引对象构建小的索引树,再将小的索引树整体插入大的索引树中去。聚类方法也被引入空间索引时的节点划分中[8]。GBI采用k-means聚类将数据集划分为多个组群和离群值,一个组群建立一颗单独的索引树,反复采用STLT来构建索引树。SCB方法也将插入数据分为聚类数据与离群数据。与STLT不同的是,SCB依据第k层节点的最小外接矩形(minimum bounding rectangle,MBR)对插入的数据进行聚类。TGS R树、OMT方法面向数据的批量加载,批量插入效率不高。STLT、GBI、SCB试图构建小的索引树,将小的索引树整体插入基态索引树中。
自下而上的批量处理主要包括排序、聚类与Buffer树[9]等方法。lowx packed R树[10]通过对MBR角点的x或者y坐标排序、分组,一次一层构建整个树。Hilbert Pack R树[11]引入空间填充曲线来改进lowx Packed R树中的排序方法。STR树[12]采用递归网格排序方法,以划分矩形为建树单位,自下而上一次一层生成整个索引树。k-way R树[13]引入k-means聚类方法对数据进行聚类,一个聚类对应一个节点,自下而上构建整个树。Buffer树将空间索引树结构关联一个基于缓存的临时数据结构,批量构建整个树。自下而上的构建方法能够显著提高索引构建效率而且能够保证查询性能,但均需要数据集的整体信息,适用于静态数据。
不管是自上而下还是自下而上的空间索引方法,均存在两个难点:①批量操作的基本粒度的定义;②局部更新操作对索引树的整体影响。lowx packed R等将排序、分组的结果作为批量操作的基本单元。该类方法不适用于具体复杂几何形态的线、面对象。GBI、k-way R树等采用聚类方法来定义批量操作基本单元的方法也存在不足。首先,均匀分布的数据没有聚类前提。其次,划分聚集分布的数据时容易出现数据倾斜现象;Merging R树方法试图通过小索引树整体插入大索引树的方法来解决索引树的批量更新问题。但是,将小索引树插入基态索引树的过程中依然需要解决插入后节点间的空间重叠度调整等问题。而且,小索引树的构建参数需要与基态索引树的构建参数完全匹配。Buffer树引入缓存机制仅能延迟索引树的整体更新,不能避免局部更新带来的整体重构。
本文以空间分布模式作为索引树构建的切入点,针对难点1,提出基于空间分布模式探测的空间数据划分方法,设计自上而下与自下而上相结合的索引树构建方法。针对难点2,则采用基于空间分布模式变化检测的索引更新方法。
2 Pattern-tree结构描述
空间划分方法是树状空间索引的核心问题之一,其附带的问题包括划分区域的重叠度、划分区域的数据量均衡以及同组对象的空间邻近性等。空间划分与聚类相同点都是为了维护组内对象相似、组间对象相离。与聚类不同的是,空间索引中的空间划分还需要考虑组间对象数据量均衡、组间空间重叠度最小、组间查询效率均衡等。文献[14]已经证明多目标的空间划分问题是一个NP完全问题。本文不试图给出空间划分的多目标求解方法,而是结合Hilbert空间填充曲线和空间分布模式分析方法,提出一种同时顾及空间邻近、分组数据量、组间空间重叠度等条件的空间数据划分方法。Hilbert曲线具有很好的空间邻近性,能够保证Hilbert编码连续的实体在空间上的最大程度的邻近[15]。但是Hilbert曲线用于空间索引构建还存在3个问题:①Hilbert曲线某种程度上反映了空间邻近性,但没有直接反映数据的空间分布模式。空间分布模式直接决定了空间划分的组间空间重叠度、数据量均衡、同组对象的空间邻近性,间接决定了叶子节点的扇入、扇出度与叶子节点查询操作的负载平衡;②Hilbert曲线与Rn空间之间并非双向映射,空间上邻近的对象其Hilbert编码不一定邻近,仅依据Hilbert编码来进行数据划分,可能带来硬分割而破坏组内对象的空间聚集性;③Hilbert曲线能够一定程度上反映空间数据的聚集程度,但无法直接反映一组Hilbert编码相同或者相近的空间数据内部的离散程度。同组对象之间的离群值将降低组内数据的聚集程度,可能会导致组间出现大范围的空间重叠,带来空间查询时的多路径搜索。
如图 1所示,本文采用Hilbert空间填充曲线对索引对象进行编码。针对问题①,引入空间模式分析方法对索引对象进行空间模式分析,将其进行空间划分,得到组内相似、组间相异、组间数据量均衡的数据块,称之为Pattern。针对问题②、③,如图 1(a)所示,提出一种Hilbert编码异常值的检测方法,将Pattern中的对象划分为正常值和异常值(可能存在0个或者多个异常值,具体定义与算法描述详见3.1)。以Pattern作为空间索引树叶子节点的构建单位,由下至上,一次一层,批量构建空间索引树Pattern-tree见图 1(b)。对异常值则采用自上而下的方式进行:从根节点开始,遍历索引节点,如果将异常值插入某个节点后,该节点的最小外接矩形变化最小,则将该节点作为插入节点。如果该节点不是数据节点,则继续遍历其子节点,直到异常值插入数据节点中。
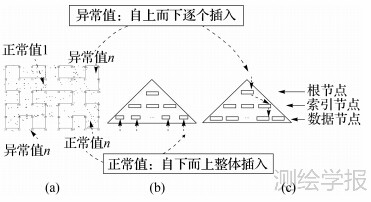 |
| 图 1 Pattern-tree构建示意图 Fig. 1 Schematic diagram of Pattern-tree |
与四叉树[16]、R树[17]等在索引树结构上相同的是,Pattern-tree包括根节点、索引节点和数据节点。根节点,全局唯一,可以包括若干索引节点。索引节点可以包括索引节点或者数据节点。数据节点处于索引树的最底层,包含若干索引对象(见图 1(c))。数据节点可描述为(I,tuple-identifier),其中,tuple-identifier表示一个n维的待索引对象,I是这个叶子结点中所有待索引对象的最小外接矩形。索引节点可描述为(I,child-pointer),其中,child-pointer是指向子节点的指针,I是覆盖所有子结点的最小外接矩形[16]。Pattern-tree是平衡树,任意对象离根节点的距离相等,查询期望值相等。与其他索引在结构上不同的是,节点容量与溢出处理方面,R树完全依赖于节点的容量,节点填充度为50%[17],达到上限则触发节点分裂,达到下限则触发节点合并。由于空间分布本身的不均匀,由数据量驱动的节点分裂和合并操作容易产生高空间重叠度而带来的低效空间索引。Pattern-tree放弃数据驱动而采用空间分布模式驱动,以Pattern作为节点,Pattern仅设定数据量上限。
索引树平衡性与索引树高度方面,KD树[18]、四叉树为非平衡树,数据节点的深度因空间数据分布不同,可能会有较大的差异。如在数据密度较大的区域数据节点较深,密度较小的区域数据节点较浅。KD树在最坏的情况下,n个对象的KD树的高度为n[18]。文献[19]给出了R树高度计算公式
式中,N为数据记录总数;ci为节点容量;f为节点平均容量。Pattern-tree包括数据节点、索引节点两个容量参数。本文给出Pattern-tree高度计算公式为 式中,N、f参数同R树;Ci为索引节点容量;Cd为数据节点容量。R树依据节点容量进行节点分裂与树的生长,Pattern-tree则同时依据索引节点容量和数据组群分布进行节点分裂与树的生长。易知,当索引节点容量相等时,若数据节点容量小于索引节点容量,Pattern-tree的高度要小于R树的高度,能有效减小索引路径的长度。若节点分裂算法和节点访问参数相同,则能有效提高搜索效率。Pattern-tree中索引节点容量Ci反映组群的个数,数据节点容量Cd反映对象的个数,具有明确的数据含义,容易根据不同类型的数据来定义容量值。3 Pattern-tree关键算法 3.1 基于空间模式分析方法的空间数据划分
本文采用文献[19]中的分散性指数来判断空间分布类型。若实体呈规则分布或者随机分布,则采用等间隔划分与离群值调整的方法获得分组结果;若实体呈聚集分布,则进行迭代寻优获得分组结果。
本文将问题①、②中出现的离群值和非正常值统称为异常值,与之对应的则称为正常值。本文采用Hilbert编码与距离的半变异函数来区分异常值与正常值。如式(3)所示,半变异函数(空间距离的函数)将Hilbert编码的方差作为变量
式中,d表示空间距离;N(d)表示距离为d的数据对(pair)的个数;Hi表示第i个对象的Hilbert编码;Hi+d表示距离第i个对象为d的某个对象的Hilbert编码。依据式(3),空间距离较小,Hilbert编码差异较大的点(见图 2中A)所对应的半变异函数值较大;空间距离较大,Hilbert编码也不同的点(见图 2中B)所对应的半变异函数值也较大。通过半变异函数值可寻找到离群值。
对于离群值,本文定义了一个反映组内对象聚集特征的目标函数来进行调整。如式(4)所示,本文将聚集特征描述为组内对象Hilbert离差平方和(Et)和组间离差平方和(E)两个指标。
 |
| 图 2 异常值示意图 Fig. 2 An examples dataset with outliers |
式中,k为分组个数;t为组别标识;nt表示第t组对象个数;ht为t组Hilbert码均值;hi为t组第i个Hilbert码。
聚集分布的数据空间划分的具体步骤是:
(1)首先对SH进行自然裂点划分,将整个集合分解为k个组,SH={g1,g2,…,gn},0
(2)对(1)得到的分组gn,尝试将离群对象hi置入其他分组,并同时比较E值。若将hi置入gm后,E减少最多,则将hi置入gm,完成一次组内离群对象调整。若E不变,则将hi置入对象个数较小的一个分组(数据量补偿策略)。
(3)对k个组分别进行离群值调整,完成一次整体迭代。
(4)重复进行(3),直至E不再减少。
Hilbert码的邻近性间接反映了实体之间的空间邻近性与聚集特征,因此该方法能够顾及实体之间的空间聚集特征;在离差平方和相等的情况下,采用数据量补偿策略,可以同时顾及组间的数据量均衡;通过离群值的调整,能够有效降低组间空间重叠度。
3.2 基于空间分布模式变化检测的批量插入
插入对象后,空间索引的均衡性可能被破坏,被插入的节点也可能上溢。简单的局部变化可能会带来索引树复杂的整体调整。本文通过空间分布的变化检测来实现数据更新后索引树的调整。当增加数据批量插入树节点后,通过分散性指数对分布式模式进行检查,如果分布模式没有发生变化,则增加数据引起的仅是索引树的数据量上的变化而不是结构上的变化,若分布模式发生了变化,则增加数据引起的是索引树的结构的变化,需进行数据节点迭代调整。完整的插入流程如图 3所示。
(1)设定批量插入操作中的对象个数参数k。
(2)插入对象前进行根节点是否存在判断。若根节点不存在,则直接将对象插入置入缓存。若根节点存在,则再对待插入对象进行范围判断。若插入对象落入现有Pattern-tree索引节点范围内,则通过节点范围判断寻找到包含该对象的数据节点。若同时有多个数据节点包含该对象,则增加到对数据节点MBR影响最小的数据节点中。若有多个数据节点插入后MBR没有变化,则插入到节点数据量较小的一个数据节点中。
(3)若待插入对象不在现有Pattern-tree索引节点范围内,则首先置入插入缓存。当达到插入缓存容量上限时,采用3.1节中描述的方法,对缓存内所有对象进行空间划分,区分正常值与异常值。对正常值构建Pattern-tree数据节点,并将其插入初始Pattern-tree中。若Pattern-tree根节点不存在,则将新构建的数据节点作为根节点的子节点。对异常值采用自上而下的方式插入数据节点中。
(4)当完成k次插入操作后,对Pattern-tree数据节点范围内的所有对象进行分散性指数计算,若分布模式没有发生变化,则按照(2)中的插入规则插入对象,并进行节点上溢检查。若有节点溢出,则选择子节点数最大的一个节点,按照3.1中所述的方法进行二路划分。若没有则直接完成增量插入。
(5)若分散性指数表明Pattern-tree内的对象分布模式发生了变化,则依据目标函数进行逐步迭代求解;若由聚集分布变化为随机分布,则目标函数为描述随机分布水平的分散性指数;若由随机分布转变为聚集分布,则目标函数为描述聚集水平的E。
(6)迭代求解结束即完成批量插入。
4 试验验证
采用江苏省境内真实数据对本文提出的数据划分、空间索引构建和查询方法进行验证。图 4中数据集A是河流和山地分割下的居民点数据,包含1588个点对象。数据集B为超市、加油站等兴趣点数据,包含619276个点对象。数据集C为道路网数据,包含241331个线对象。数据集A用来测试本文提出的空间划分算法。数据集B、C用于测试Pattern-tree的构建效率与窗口查询效率。试验环境为:IBM Thinkpad T410s,Inter(R)core(TM)i5 CPU,3GB 内存,Windows 7操作系统。
本试验选取GBI、STLT来与本文方法对比。GBI方法中采用k-means方法来进行数据划分,STLT采用R树方法来进行数据划分。试验中采用线性R树分组算法来实现STLT。采用ArcGIS中Average Nearest Neighbor Distance点模式分析工具对数据集A分析,结果表明该数据呈聚集分布且显著性水平为0.01。按照本文分布模式指标,对包含一个以上点对象的Hilbert区块进行样方统计分析。结果表明数据集A在受限区域内显著的呈随机分布,可采用算法时间复杂度和空间复杂度都比R树线性分组和k-means分组方法小的等差划分方法来进行数据划分。将试验数据划分为5组,用虚线表示每组的MBR。结果如图 5所示,(a)为GBI方法划分结果,(b)为STLT方法划分结果,(c)为本文方法初始划分结果,(d)为离群值调整后的本文方法划分结果。
由图 5可知,k-means方法能够取得较好的空间聚集性。但是组间空间重叠度较大。R树方法虽然能够取得较好的节点利用率,但是由于没有顾及空间分布特征,组间空间重叠度较大。结果C中用圆圈标识出来的对象即为本文3.1节描述的Hilbert离群值。离群值对空间划分后的组间重叠度产生了较大影响。进行离群值调整后的结果优于GBI、STLT方法。
本文选择STLT、SCB、GBI 3种支持批量操作的空间索引与本文方法进行对比。采用C++语言实现4种索引结构。采用磁盘文件作为外存,选择4KB作为叶子节点容量上限。考虑到:①4种方法的算法原理不一致,步骤不能一一对应,索引构建算法和步骤均有较大差异;②算法实现过程中,代码实现细节对测试结果也会产生影响。因此,本文不进行单项技术指标的定量比较,而是借鉴文献[7—10]中的测试方法,将索引构建和查询过程中页面I/O访问次数作为衡量空间索引构建和查询效率的指标。4种方法均完整地统计数据划分、索引构建等环节。分别选取占总量20%、40%、60%、80%与100%的数据子集来构建初始索引树。批量插入的数据为100。离群值比例选择为10%。数据集B、C的试验结果如图 6、图 7所示。由图可知,不管是点数据还是线数据,Pattern-tree构建效率均优于其他3种空间索引。其主要原因是,STLT中小树的构建依然是OBO方式。GBI、SCB引入了聚类方法,以聚类作为操作对象,效率要优于STLT方法。其中,SCB依据先验知识来进行聚类,因此效率高于GBI方法。GBI、SCB方法直接采用聚类方法,与STLT、SCB、GBI相比,Pattern-tree增加了空间分布模式探测步骤。但是,仅涉及均值、方差等的计算。Pattern-tree中仅包含节点容量上限,避免了节点分裂过程中的下溢检查,减少了节点的合并操作;Pattern-tree批量插入过程中通过空间分布模式变化检测,可以有效减少索引树的整体调整。因此,Pattern-tree具有较高的构建效率。
定义整个数据集空间范围的1/4、1/16、1/128 三种大小的窗口查询范围。随机产生查询窗口的起始位置,每个窗口查询执行10次,取I/O访问次数平均值进行效率对比。数据集A、B的试验结果如图 8、图 9所示。由图可知,无论是点数据还是线数据,Pattern-tree查询效率均优于其他3种空间索引。其主要原因是:①Pattern-tree中采用Hilbert曲线对实体进行编码,能够保证一定的空间邻近性,能够保证空间上邻近的地理要素在物理存储上尽量连续,能够有效避免页面的跳跃读取,减少页面访问;②Pattern-tree分别设置索引节点容量和数据节点容量,可有效降低索引树的高度,缩短数据节点到根节点的路径长度;③Pattern-tree采用自上而下的方式插入离群值,有利于降低组间重叠度,减少多路径搜索。
本文认为支持批量操作的索引构建难点在于批量操作的基本粒度的定义以及局部更新操作对索引树的整体影响。本文以空间分布模式作为索引树构建的切入点,针对问题一,在Hilbert空间填充曲线的基础上引入空间分布模式分析方法,设计了一种兼顾空间聚集性、分组数据量等条件的空间划分方法。该方法能够保证空间上邻近的地理实体在逻辑/物理存储介质上尽量连续,能够有效避免空间查询过程中的跳跃访问。该方法能够兼顾空间聚集性、数据量、空间重叠度3种约束条件,能够避免单纯采用聚类方法所带来的数据倾斜问题,能够避免单纯采用空间索引方法所带来的空间重叠问题。索引构建时,以划分单元为单位,正常值采用自下而上,异常值采用自上而下,能够同时顾及索引的构建效率和索引的构建质量。针对问题二,针对具体变化对整体的影响问题,提出一种空间分布模式变化检测的动态更新方法,能够有效避免索引的周期性重建。
文献[11、20—21]等均在空间索引或者空间划分中引入了Hilbert填充曲线。本文在Hilbert编码反映空间邻近性的基础上进一步进行空间分布模式分析,对Hilbert编码对象进行多目标空间划分,将划分单元作为批量操作的基本单位,取代OBO方式,实现了空间索引的快速构建。本文还分析了Hilbert编码在反映空间邻近性时的异常值问题,给出了异常值提取方法,设计了自上而下与自下而上相结合的构建方法,能够同时兼顾构建与查询效率。本文的后续工作还包括最优的初始比例计算以及三维对象批量操作问题。
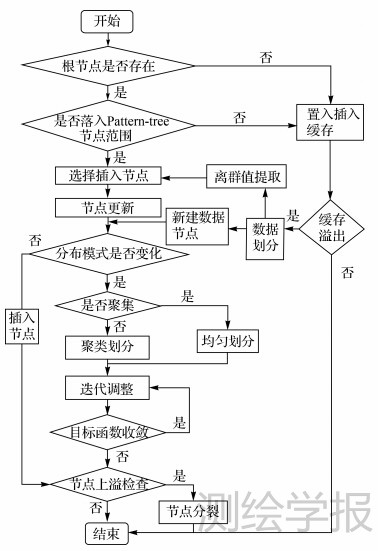
图 3 批量插入流程图
Fig. 3 Flow chart of buck insertion 
图 4 试验数据
Fig. 4 Sample data sets 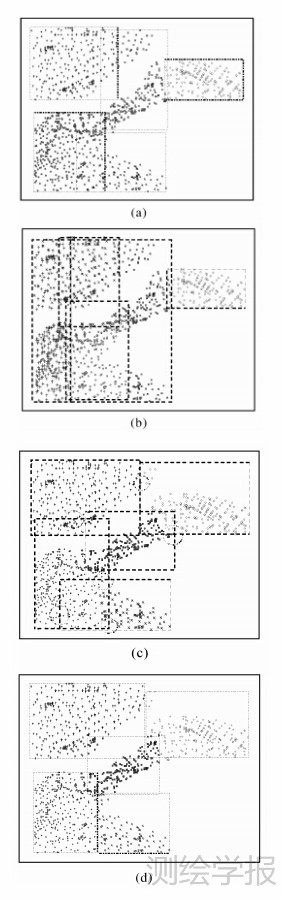
图 5 数据集A划分结果
Fig. 5 Result of partitioning of the dataset A 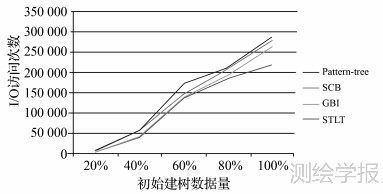
图 6 数据集B的4种空间索引插入效率对比
Fig. 6 Comparison of insertion costs of four methods for real datasets B 
图 7 数据集C的4种空间索引插入效率对比
Fig. 7 Comparison of insertion costs of four methods for real datasets C 
图 8 数据集B的4种空间索引查询代价对比
Fig. 8 Comparison of query costs of four methods for real datasets B 
图 9 数据集C的4种空间索引查询代价对比
Fig. 9 Comparison of query costs of four methods for real datasets C
| [1] | WANG Yanmin, GUO Ming. A Combined 2D and 3D Spatial Indexing of Very Large Point-cloud Data Sets[J].Acta Geodaetica et Cartographica Sinica,2012,41(4):605-612.(王晏民,郭明.大规模点云数据的二维与三维混合索引方法[J].测绘学报,2012,41(4):605-612.) |
| [2] | AGHBARI Z A. CTraj: Efficient Indexing and Searching of Sequences Containing Multiple Moving Objects[J]. Journal of Intelligent Information Systems, 2012, 39 (1): 1-28. |
| [3] | GARCIA Y, LOPEZ M, LEUTENEGGER S T. A Greedy Algorithm for Bulk Loading R-trees[C]//Proceedings of the 6th ACM-GIS.Washington DC:[s.n.],1998:163-164. |
| [4] | LEE T, LEE S. OMT: Overlap Minimizing Top-down Bulk Loading Algorithm for R-tree[C]//Advanced Information Systems Engineering. Klagenfurt:[s.n.],2003: 69-72. |
| [5] | CHEN L, CHOUBEY R, RUNDENSTEINER E A. Merging R-Trees: Efficient Strategies for Local Bulk Insertion[J]. Geoinformatica, 2002, 6(1): 7-34. |
| [6] | CHOUBEY R, CHEN L, RUNDENSTEINER E A. GBI: A Generalized R-tree Bulk-insertion Strategy[C]//Proceedings of SSD.Hong Kong:[s.n.],1999:91-108. |
| [7] | LEE T, MOON B, LEE S. Bulk Insertion for R-tree by Seeded Clustering[C]//Database and Expert Systems Applications.Prague:[s.n.],2003:129-138. |
| [8] | GONG Jun,ZHU Qing,ZHANG Yeting,et al. An Efficient 3D R-tree Extension Method Concerned with Levels of Detail[J]. Acta Geodaetica et Cartographica Sinica,2011,40(2):249-255. (龚俊,朱庆,张叶廷,等.顾及多细节层次的三维R树索引扩展方法. 测绘学报,2011,40(2):249-255.) |
| [9] | BERCKEN J, SEEGER B, WIDMAYER P. A Generic Approach to Bulk Loading Multidimensional Index Structures[C]//Proceedings of the 23rd VLDB.Athens:[s.n.],1997:406-415. |
| [10] | ROUSSOPOULOS N, LEIFKER D. Direct Spatial Search on Pictorial Databases Using Packed R-trees[C]//Proceedings of ACM SIG-MOD.Austin:[s.n.],1985:17-31. |
| [11] | KAMEL I, FALOUTSOS C. On Packing R-trees[C]//Proceedings of CIKM. Washington DC:[s.n.],1993: 490-499. |
| [12] | CHEN L, CHOUBEY R, RUNDENSTEINER E A. Bulk-insertions into R-trees Using the Small-tree-large-tree Approach[C]//Proceedings of ACM-GIS. Washington DC:[s.n.],1998:161-162. |
| [13] | GAVRILA D M. R-tree Index Optimization[C]//Proceedings of the Sixth International Symposium on Spatial Data Handling. Edinburgh:[s.n.],1994:771-791. |
| [14] | SHEKHAR S, RAVADA S, KUMAR V. Declustering and Load-balancing Methods for Paralleling Geographic Information Systems[J]. IEEE Transactions on Knowledge and Data Engineering, 1998,10(4):632-655. |
| [15] | MOON B, JAGADISH H V, FALOUTSOS C. Analysis of the Clustering Properties of the Hilbert Space-filling Curve[J]. IEEE Transactions on Knowledge and Data Engineering, 2001,13: 124-141. |
| [16] | SAMET H. Hierarchical Representation of Collections of Small Rectangles[J]. ACM Computing Surveys, 1998,20 (4): 271-309. |
| [17] | GUTTMAN A. R-trees: a Dynamic Index Structure for Spatial Searching[C]//Proceedings of ACM SIGMOD International Conference on Management of Data. Boston:[s.n.],1984:47-57. |
| [18] | BENTLEY J L, FRIEDMAN J H. Data Structures for Range Searching[J]. ACM Computing Surveys,1979, 11 (4): 397-409. |
| [19] | WANG Yuanfei, HE Honglin. Spatial Data Analysis[M].Beijing:Science Press,2007. (王远飞, 何洪林. 空间数据分析方法[M].北京:科学出版社,2007.) |
| [20] | ZHOU Yan, ZHU Qing, ZHANG Yeting. A Spatial Data Partitioning Algorithm Based on Spatial Hierarchical Decomposition Method of Hilbert Space-filling Curve[J]. Geography and Geo-Information Science,2007,23(4):13-17. (周燕,朱庆,张叶廷.基于Hilbert曲线层次分解的空间数据划分方法[J]. 地理与地理信息科学,2007,23(4):13-17.) |
| [21] | LU Feng, ZHOU Chenghu. A GIS Spatial Indexing Approach Based on Hilbert Ordering Code[J]. Journal of Computer-Aided Design & Computer Graphics, 2001,13(5):424-429. (陆锋,周成虎.一种基于Hilbert排列码的GIS空间索引方法[J].计算机辅助设计与图形学学报,2001,13(5):424-429.) |