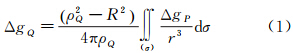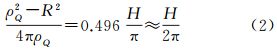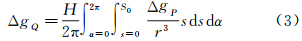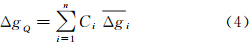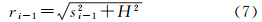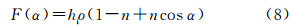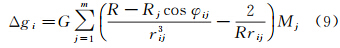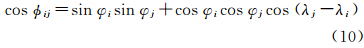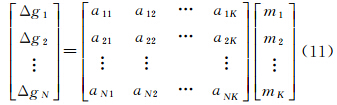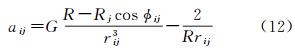2. 西安测绘研究所,陕西 西安 710054
2. Xi'an Institute of Surveying and Mapping, Xi'an 710054, China
1 引 言
航空重力测量是获取局部区域重力场信息的有效手段,其测量效率高、精度均匀,分辨率较高,我国于2002年自行成功研发了航空重力测量系统(CHAGS),并相继在大同、哈尔滨等试验中获得了较好的测量结果[1]。在国家重大专项海岛礁测绘工程中,利用航空重力测量技术已经在渤海、山东半岛、东南沿海等区域开展了大规模的测量工作,获取了大量实测重力数据。除中国外,美国、俄罗斯、澳大利亚、意大利、日本等国也利用航空重力测量系统在复杂、困难地区进行重力测量工作,航空重力数据在陆海大地水准面统一与精化、重力数据融合中发挥着重要作用[2, 3, 4, 5, 6, 7, 8, 9]。航空重力测量数据在不同区域有不同的测量精度,在山区和平原地区已有文献给出了其精度评估结果[10, 11, 12, 13, 14, 15, 16, 17],随着航空重力在海域的广泛应用,其精度评估也成为一个关键问题。精度评估大致可从两方面入手:一是利用不同测线形成的交叉点不符值进行平差分析得出内部精度,二是利用外部基准重力数据对空中测量数据进行直接评估从而得到比较准确的外部精度。由于航空重力测量获得的是空中扰动重力数据,而实际上高精度重力数据位于地面或海面,因此如何利用地表的重力数据评估空中重力数据是精度评估的关键技术问题。本文将从物理大地测量基础理论出发研究近海航空重力测量的精度评估方法,并在实际测量区域开展计算分析。
2 精度评估方法 2.1 泊松积分法评估利用泊松积分公式由地面重力数据向上延拓可解析获得测量高度处的重力数据[18, 19],以该数据作为基准进而与空中的测量数据直接进行比较获得其测量精度。由地面点的重力异常数据Δgp推求空中一点Q的重力异常的泊松积分表达式为
式中,ρQ表示Q点的向径;R表示球半径;r=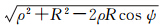 ,ψ表示单位面元dσ与Q点的球心角距。在实际应用中,利用平面极坐标进行改化,当待求点高度H等于100 km时
因此当待求点高度小于100 km时,
,ψ表示单位面元dσ与Q点的球心角距。在实际应用中,利用平面极坐标进行改化,当待求点高度H等于100 km时
因此当待求点高度小于100 km时,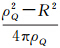 可认为等于
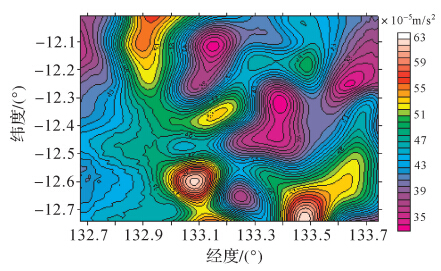
可认为等于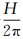 。
。此时式(1)可改写为
式中,s、α分别表示平面极坐标中的极距和方位角,若将积分区域分成许多环,则 式中,Δgi为第i环的平均重力异常值;Ci为相应的系数,按下式计算 式中 式中,si-1和si 为第i环的内、外半径。 2.2 点质量法评估假设分布于地下的扰动质量为k个扰动质点Mjj=(1,2,…,K),则地面外任一点P的扰动位可以由万有引力定律算出,即
式中,rj为第j个点质量至P点的距离。假定地面Σ是半径为R的球面,点质量Mj与球心的距离为Rj,则Σ面上任意点i的重力异常Δgi可按下式求得
式中,G表示万有引力常数;rij和φij分别为点质量Mj和点i之间的距离和球心角距;φij可由计算点P和扰动质点Mj的地心经纬度(φi,λi)和(φj,λj)求
对于地面Σ上的N个重力异常点,它们与扰动质点的关系可由式(9)表示成以下矩阵形式
式中以式(11)作为观测方程,当已知重力异常数N大于或等于点质量数K时,即可使用最小二乘方法求解点质量Mj,利用建立的点质量模型可以计算扰动位进而计算空中的重力异常[20, 21],与航空重力测量数据进行比较获得其测量精度。
3 试验与分析选择两个试验区进行分析,第1个试验区位于澳大利亚北部West Arnhem Land近海区域,航空重力测量采用了俄罗斯研制的GT-1A航空重力仪,测量高度0.655 km,分辨率2′,示意图见图 1。测量区域地面的陆地、船测重力数据分辨率约1′,数据分布范围见图 2,该数据由澳大利亚地理科学局(Australia’s National Geoscience Agency)提供。
 |
| 图 1 澳大利亚试验区航空重力数据等值线图Fig. 1 Airborne gravity data of Australia West Arnhem Land area |
 |
| 图 2 澳大利亚试验区地表重力数据等值线图Fig. 2 Land and sea gravity data of Australia West Arnhem Land area |
点质量模型的建模过程如下:首先,选取EGM2008前36阶重力位模型作为参考重力场[22],相当于全球5°×5°平均重力异常,其次,将计算区域1°×1°的每个网格的平均重力异常减去由36阶重力位模型计算的平均重力异常,得到1°×1°网格的剩余重力异常并以其作为观测量求解对应的点质量M1°,埋藏深度一般采用与质点间距大致相等的深度比较合适[19, 20],因此,对于1°×1°网格埋藏深度取100 km。对于每个20′×20′的网格平均重力异常减去重力场模型和M1°计算得到的对应该网格的重力异常值,以得到的残差重力异常计算对应20′网格的点质量M20′。对于5′×5′和1′×1′网格的处理方式同上面类似,不再详述。每种格网数据的覆盖范围及埋藏深度见表 1。
| 数据 | 格网分辨率 | |||
| 1°×1° | 20′×20′ | 5′×5′ | 1′×1′ | |
| 覆盖范围 | 30°×30° | 10°×10° | 4°×4° | 1°30′×1°30′ |
| 埋藏深度/km | 100 | 40 | 10 | 2 |
分别利用泊松积分法和点质量法获得相应空中的重力数据,而后与航空重力测量数据进行比较,其统计结果见表 2。
| 10-5 m/s2 | ||||
| 方法 | 最大值 | 最小值 | 平均值 | 标准偏差 |
| 泊松积分 | 11.63 | -13.05 | 0.09 | 2.81 |
| 点质量 | 19.60 | -13.70 | 0.32 | 2.95 |
通过表 2可以看出,两种方法对航空重力测量数据的评估精度大致相当,利用泊松积分法获得的结果略优,总体上,澳大利亚West Arnhem Land区域对于2′分辨率的航空重力测量精度优于3×10-5 m/s2。若将两种方法向上延拓获得的2′分辨率数据格网化为5′分辨率,同时将空中测量数据也格网化为5′,则比较结果表明澳大利亚此次航空重力测量5′分辨率的数据精度优于2×10-5 m/s2。
第2个试验区位于我国渤海区域,该区域航空重力测量于2009年完成,采用的是我国的CHAGS系统,数据分辨率为5′,测量高度约2400 m,该区域航空重力测线分布图见图 3。根据文献[13]研究表明,CHAGS系统测量数据在经过系统误差补偿后系统差会明显下降,因此在评估渤海区域测量数据之前,对观测数据中的水平加速度改正项重新进行了处理。
首先进行交叉点平差,在去除个别异常点后平差结果见表 3。
| 10-5 m/s2 | ||||
| 交叉点数量 | 不符值均值 | 最大值 | 最小值 | 标准偏差 |
| 2630 | -0.14 | 46.48 | -89.26 | 4.13 |
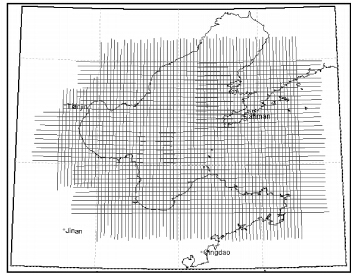 |
| 图 3 渤海区域航空重力测线分布图Fig. 3 Airborne surveying lines of Bohai area using CHAGS |
其次综合利用这一区域陆地、海洋上的重力数据形成了36°N—41°N、116°E—124°E范围内5′分辨率的地表重力数据。为了对整体和局部都有深入的分析,在对整个空中测量区域进行评估的同时也选取空中5个1°×1°范围(38°N—39°N,118°E—123°E)的区域进行评估,评估方法采用泊松积分法和点质量法,最终得到渤海湾区域航空重力数据的精度统计结果见表 4。
| 10-5 m/s2 | ||
| 区域 | 标准偏差(泊松积分法) | 标准偏差(点质量法) |
| 38°N—39°N,118°E—119°E | 3.23 | 3.51 |
| 38°N—39°N,119°E—120°E | 1.54 | 1.69 |
| 38°N—39°N,120°E—121°E | 4.15 | 4.10 |
| 38°N—39°N,121°E—122°E | 4.63 | 4.72 |
| 38°N—39°N,122°E—123°E | 2.31 | 2.56 |
| 整个区域 | 3.26 | 3.38 |
对比表 3、表 4可以看出,内部交叉点平差与外部重力数据的评估得到评估结果存在不同,外部评估结果表明此区域的航空重力数据整体精度达到3×10-5 m/s2,这个精度要比内部评估精度高约1×10-5 m/s2,这个原因可能是交叉点平差的对象是点值,而外部数据评估的是5′分辨率的格网值。通过计算也发现,对水平加速度改正项进行重新处理后,航空重力数据中的系统偏差(约3×10-5 m/s2)基本得到消除。
4 结 论航空重力测量目前在近海区域得到了广泛应用,为了对近海区域的航空重力数据进行有效评估,本文从内部交叉点平差和外部重力数据两个方面入手在国内外近海区域开展了计算分析,得到以下结论:
(1) 泊松积分法和点质量法作为两种外部评估手段虽然处理思路不同,但从最终结果看,两种方法都可用于空中重力数据的评估且精度基本一致。澳大利亚West Arnhem Land区域的数据评估结果表明,其2′分辨率数据的测量精度优于3×10-5 m/s2,以此为参考计算获得的5′分辨率的数据精度优于2×10-5 m/s2,通过评估可以看出澳大利亚此次使用GT-1A测量系统的航空重力测量的精度和分辨率较高,代表了国际航空重力测量的先进水平。
(2) 内部交叉点平差和外部数据评估得到的评估结果并不完全相同,外部重力数据评估表明,渤海区域CHAGS系统对于5′分辨率的重力数据其精度优于3.5×10-5 m/s2。计算也表明,水平加速度改正是引起航空重力数据系统偏差的主要原因,如果不进行有效改正,则航空重力数据中可能会存在约3×10-5 m/s2偏差。
(3) 综合国内外情况可以推断,对于现阶段的近海区域5′分辨率的航空重力测量,其测量精度达到或优于3×10-5 m/s2是符合现实且有说服力的。
| [1] | SUN Zhongmiao. The Theory Method and Application of Airborne Gravimetry[D].Zhengzhou:Information Engineering University,2004. (孙中苗.航空重力测量理论、方法及应用研究[D].郑州:信息工程大学,2004.) |
| [2] | ELLMANNA,HWANG Y S. First International Symposium of the International Gravity Field Service[R].Istanbul:[s.n.],2006. |
| [3] | JIRO SEGAWA,JOHN JOSEPH E,EIJI NAKAYAMA,et al. Application of Gravimetry by Hellicopter to Identify Marine Active Faults and Improve Accuracy of Geoid at Coastal Zones[C]Sapporo:[s.n.//Proceedings of IAG General Assembly. ],2003. |
| [4] | ZHAI Zhenhe, Sun Zhongmiao. Adaptive Fusion Method of Multi-source Gravity Data in Bohai Area[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):1-5.(翟振和,孙中苗. 渤海湾多源重力数据的自适应融合处理[J].测绘学报,2010,39(5):1-5.) |
| [5] | ZHOU Jianxin,LIU Haojun,WANG Shoutan, et al. The Application of Airborne Gravity Survey to Earth Science in Foreign Countries[J]. Geophysical and Geochemical Exploration, 2004,28(2):119-123.(周坚鑫,刘浩军,王守坦,等.国外航空重力测量在地学中的应用[J].物探与化探,2004,28(2):119-123.) |
| [6] | NOVAK P, KERN M, SCHWARZ K P.On Geoid Determination from Airborne Gravity[J]. Journal of Geodesy,2003, 76: 510-522. |
| [7] | FORSBERG R, OLESEN A, BASTOS L, et al.Airborne Geoid Determination[J]. Earth Planets Space, 2000,52:863-866. |
| [8] | FADI A,BAYOUD, MICHAEL G. Two Different Methodologies for Geoid Determination from Ground and Airborne Gravity Data[J]. Geophysical Journal International,2003,155:914-922. |
| [9] | SHI Pan,WANG Xingtao. Frequence Domain Analysis for the Determination of Terrestrial Land Mean Gravity Anomaly from Airborne Gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4): 301-308.(石磐, 王兴涛. 空中测量地面平均重力异常的频域分析[J]. 测绘学报, 1995, 24(4): 301-308.) |
| [10] | WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004,33(1):33-37.(王兴涛,石磐,朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解[J].测绘学报,2004,33(1):33-37.) |
| [11] | WANG Xingtao,XIA Zheren,SHI Pan,et a1.A Comparison of Different Downward Continuation Methods for Airborne Gravity Data[J].Chinese Journal of Geophysics,2004,47(6):1017-1022(王兴涛,夏哲仁,石磐,等.航空重力测量数据向下延拓方法比较[J].地球物理学报,2004,47(6):1017-1022.) |
| [12] | SUN Zhongmiao,XIA Zheren,WANG Xingtao,et al. Accuracy Evaluation of Airborne Gravimetry over Plain Area[J]. Bulletin of Surveying and Mapping,2006(10):1-5.(孙中苗,夏哲仁,王兴涛,等.平原地区航空重力测量的精度分析[J].测绘通报,2006(10):1-5.) |
| [13] | SUN Zhongmiao,ZHAI Zhenhe,XIAO Yun, et al.Systematic Error Compensation for Airborne Gravimetry[J].Chinese Journal of Geophysics,2013,56(1):47-49.(孙中苗,翟振和,肖云,等.航空重力测量的系统误差补偿[J].地球物理学报,2013,56(1):47-49.) |
| [14] | WEI M, SCHWARZ K P. Flight Test Results from a Strapdown Airborne Gravity System[J].Journal of Geodesy,1998,72: 323-332. |
| [15] | BOLOTIN Y V, POPELENSKY M Y U. Accuracy Analysis of Airborne Gravity when Gravimeter Parameters are Identified in Flight[J]. Journal of Mathematical Sciences, 2007,146(3):231-237. |
| [16] | BERZHITSKY V N, ILJIN V N, SAVELIEV E B, et al.GT-1a Inertial Gravimeter System Design Consideration and Results of Flight Tests[C]//Proceedings of 9th Saint Petersburg International Conference on Integrated Navigation Systems. Petersburg:[s.n.], 2002. |
| [17] | BOLOTIN Y V, POPELENSKY M Y.The Analysis of Accuracy of Airborne Gravimetry with Stochastic Models[J]. Aerokosmicheskoe Priborostroenie, 2003,4:42-48. |
| [18] | HELMUT MORITZ.Physical Geodesy[M]. NewYork:Springer,2006. |
| [19] | LU Zhonglian. The Theory and Method of Earth Gravity Field[M].Beijing: Liberation Army press,1996.(陆仲连.地球重力场理论与方法[M].北京:解放军出版社,1996.) |
| [20] | WU Xiaoping. The Model of Point Masses in Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 1984,23(4):6-10.(吴晓平.局部重力场的点质量模型[J]. 测绘学报,1984,23(4): 6-10.) |
| [21] | MORITZ H.Advanced Physical Geodesy[M].NING Jinsheng,GUAN Zelin,trans. Beijing: Surveying and Mapping Press,1984.(赫尔默特·莫里兹.高等物理大地测量学[M].宁津生,管泽霖,译.北京:测绘出版社,1984.) |
| [22] | ZHANG Chuanyin,GUO Chunxi,CHEN Junyong, et al.EGM2008 Model and Its Application in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(4):283-286.(章传银,郭春喜,陈俊勇,等.EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报,2009,38(4):283-286.) |