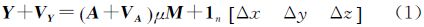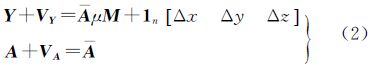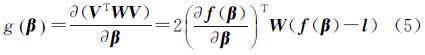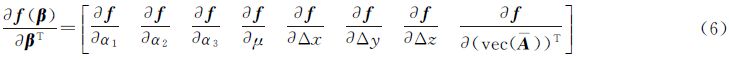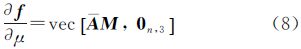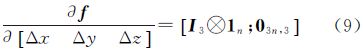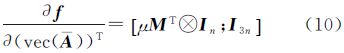2. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079
2. Research Center of GNSS,Wuhan University,Wuhan 430079,China
1 引 言
三维坐标转换模型是大地测量、摄影测量、地图投影、计算机视觉等专业领域常用的变量含误差(errors-in-variables，EIV)模型之一，模型描述了源坐标系统[X Y Z]至目标坐标系统[x y z]的函数映射关系[1]
式中，n表示坐标点个数；1n表示n×1的元素为1的向量；
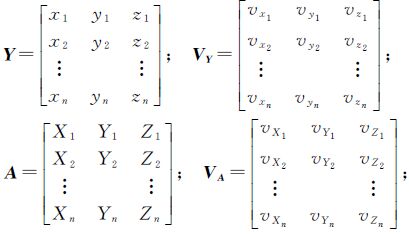
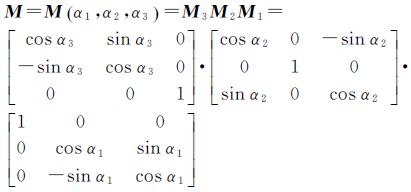
坐标转换模型的整体最小二乘估计(total least squares method，TLS)具有渐进无偏性[2]。可以看到，模型(1)的系数矩阵为[A 1n]，包含随机量与非随机量，并且向量化后的系数矩阵中的随机量呈结构性特征[3]；其次，旋转参数[α1 α2 α3]与系数矩阵呈复杂的非线性关系。因此，三维坐标转换模型无法直接采用TLS算法求解。文献[4]将式(1)转换为线性化的Gauss-Helmert模型(Gauss-Helmert model,GHM)求解，由于算法的迭代更新项存在问题[5]，得到的并不是最优的TLS解。文献[6]提出了一种仅适用于小旋转角度的TLS解。文献[7]基于Gauss-Markov模型和EIV模型的正交回归解的等价性提出了加权TLS算法，但对权阵有严格的限制条件。文献[1, 8, 9]采用迭代GHM方法推导了一般权阵条件下的加权TLS算法，迭代GHM方法尽管被认为是解决非线性问题的有效方法，但到目前为止，该方法并没有从理论上予以证明[10]。近年来，国内大地测量领域对三维坐标转换模型的TLS算法展开了研究[11, 12, 13]。文献[14]讨论了小角度、特殊权矩阵条件下的基于奇异值分解的TLS算法。文献[15]在单位权阵条件下，将旋转矩阵全部9个元素视为待估参数，构造了附有限制条件的间接平差模型，采用奇异值分解方法，得到了任意旋转角度的TLS解法。由于基于奇异值分解的TLS算法本质上属于数值解法，无法得到统计意义上的估计值，在测量中的应用受到了限制[16, 17]。文献[18]通过将式(1)转换为附有限制条件的平差模型导出了特殊权矩阵条件下的加权TLS算法。
可以看到，现有三维坐标转换模型的TLS算法均受到特殊条件限制,实际应用范围有限，如摄影测量中物方坐标系到像方坐标系的转换是大角度三维坐标系统之间的转换，不同大地基准下点的坐标测量技术手段可能不同，从而坐标点的精度不等且相关，因此，有必要研究一般情况下的TLS算法。本文通过提取系数矩阵的随机量作为待估计参数，研究了三维坐标转换模型的通用加权整体最小二乘算法，该算法适用于任意旋转角度以及一般性的权矩阵，将结构性系数矩阵，同时包含随机和非随机元素的系数矩阵等情况，纳入统一的坐标转换模型算法，能够很好地满足现代大地测量领域对高精度三维坐标转换模型估计的需要。
2 三维坐标转换的加权整体最小二乘算法为采用统一的方法求解结构性系数矩阵的EIV模型，将模型(1)中系数矩阵的随机量与坐标转换参数一并作为待估计参数，则三维坐标转换模型可描述为
式中，A表示将系数矩阵的随机量(即源坐标)作为模型的待估计参数所构成的矩阵。
经过以上变换，坐标转换的EIV模型可表示为非线性GM模型形式
式中，l=vec[Y A]表示观测向量，包含所有目标坐标和源坐标；vec是向量化符号，表示将矩阵依次按列排列成向量；V=vec[VY VA]表示观测值的改正数向量；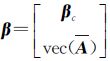
表示待求参数向量。其中除了七参数向量βc =[α1 α2 α3 μ Δx Δy Δz]T外，还包括源坐标估计向量vec(A)，f(β)=vec[AμM+1n[Δx Δy Δz],A](“，”表示下一列)。
在整体最小二乘准则下，进一步将式(3)的求解转化为经典的非线性模型的最优化问题。令式(3)中观测值l的一般性权阵为W，不限定观测数据(源坐标和目标坐标值)的精度或者相关性，式(3)的整体最小二乘最优估计可表示为以下最优化问题
导出式(4)的梯度即一阶偏导项
式(5)中，f(β)的偏导项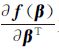
为
式中，各项梯度公式分别为
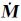i(i=1,2,3)的具体形式为
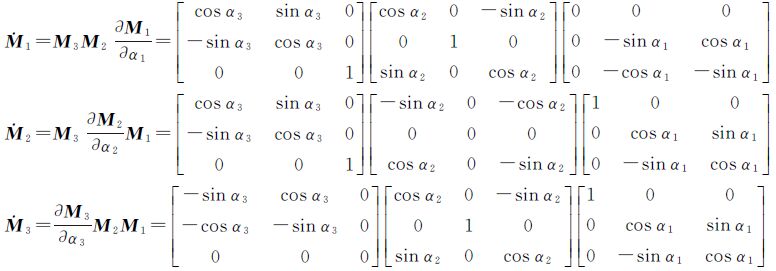
导出三维坐标转换模型的梯度公式(5)—式(10)后，根据非线性最优化理论，可以采用多种方法求解模型参数的最佳估值。如根据梯度公式,在参数的近似值处采用梯度下降法，即在反梯度方向搜索模型的最优估计值，或者采用高斯牛顿法求解等。这些方法均为非线性估计的基本方法，具体请参阅文献[19]。采用传统的大地测量求解非线性Gauss-Markov模型的算法同样可以求解模型(3)[20]。运用各种迭代算法求解坐标转换参数时，参数初始值可选取βc0=[0 0 0 1 0 0 0]T。以拟牛顿法为例，列出三维坐标转换模型式(2)的整体最小二乘算法的计算步骤如下：
(1) 给出模型的初始解βc0，根据式(5)—式(6)计算模型的梯度g(β)。
(2) 迭代计算拟牛顿法中的海森(Hessian)矩阵的近似表达式量，直到前后两次参数估计之差Δβi小于设定的正微小量
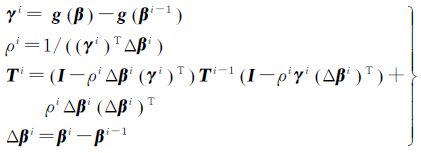
(3) 根据以下Broyden-Fletcher-Goldfarb-Shanno (BFGS)算法公式，得到三维坐标转换模型的整体最小二乘估计结果
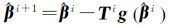
笔者选用文献[7]中大角度三维坐标转换模型实例数据，采用本文提出的算法进行计算。坐标转换数据来源于两个表面模型坐标转换的实测观测值，共包含4个公共点，相应的源坐标值和目标坐标值见表 1，模型估计结果见表 2。
| 参数 | LS(等权) | TLS(等权) | TLS(加权) |
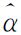 1 | 54′45.356 1″ | 54′45.356 1″ | 30′51.466 6″ |
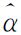| 2 | -57′47.402 9″ | -57′47.402 9″ | -4°31′21.125 5″ |
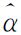| 3 | -35°49′30.616 6″ | -35°49′30.616 6″ | -33°32′19.511 1″ |
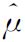 | 2.082 975 4 | 2.121 636 2 | 2.176 126 9 |
Δ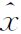 | 196.970 86 | 193.016 96 | 188.977 14 |
Δ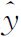 | 118.588 95 | 117.402 74 | 101.517 20 |
Δ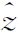 | -14.935 29 | -15.407 38 | -33.380 08 |
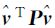 | 1 283.77 | 236.89 | 319.004 |
当坐标数据等权即权阵为单位阵(W=I24)的情况下，表 2的第2列和第3列分别为转换参数的最小二乘估计值和整体最小二乘估计值，第4列为设定坐标数据非等权情况下(W=I6⊗diag(1,4,6.25,16))的整体最小二乘估计值，表中的估计结果与文献[1, 7]一致。对比第2列和第3列数据可以看到，整体最小二乘估计结果由于同时顾及了目标坐标和源坐标的随机误差，残差平方和远小于最小二乘的残差平方和，与文献[21, 22, 23]实例中坐标转换模型的最小二乘和整体最小二乘残差平方和对比结论一致。同时，表中旋转参数的最小二乘和整体最小二乘估计结果相等，与文献[7]证明的当观测数据的权阵为一定特殊形式时，三维坐标转换模型旋转参数的最小二乘和整体最小二乘估计结果相等的结论一致。第3列和第4列数据表明，权阵对整体最小二乘估计结果影响显著，若没有采用正确的权阵，例如没有考虑坐标数据不等精度、相关性，或者权阵没有考虑到系数矩阵的结构性特点等，都会导致整体最小二乘的估计结果产生偏差。
4 结 论三维坐标转换模型是大地测量、摄影测量等众多专业领域常用的基本EIV模型之一，现代大地测量中高精度、三维动态大地坐标系统的建立对三维坐标转换模型的估计算法提出了更高的要求。现有TLS算法均受到一定限制条件的制约，如仅适用于小角度坐标转换模型、属于非统计意义上的数值解以及需要对坐标转换模型的结构性系数矩阵的权阵进行特殊处理等。本文通过将模型中的源坐标与坐标转换参数一并作为待估计参数，推导了三维坐标转换模型的TLS通用算法，该算法适用于任意旋转角的坐标转换以及一般性的权矩阵，并可直接应用于坐标转换模型结构性系数矩阵的情况。本文通过大角度三维坐标转换的实例对该算法进行了说明和验证，结果表明新算法突破了现有算法的限制条件，能有效地应用于坐标转换模型的一般情况，其通用性有利于应用中的编程实现。
| [1] | FANG Xing. Weighted Total Least Squares Solution for Application in Geodesy[D]. Hanover: Leibniz University of Hanover, 2011. |
| [2] | HUFFEL S V, VANDEWALLE J.The Total Least-squares Problem: Computational Aspects and Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1991. |
| [3] | FANG Xing. A Structured and Constrained Total Least-squares Solution with Cross-covariances[J]. Studia Geophysica et Geodaetica, 2014, 58 (1): 1-16. |
| [4] | BLEICH P, ILLNER M. Strenge Lsung der Rumlichen Koordinatentransformation Durch Iiterative Berechnung[J]. Allgemeine Vermessungs-Nachrichten,1989,96 (4):133-144. |
| [5] | POPE A. Some Pitfalls to be Avoided in the Iterative Adjustment of Nonlinear Problems[C]//Proceedings of the 38th Annual Meeting of American Society Photogrammetry. Washington DC: [s.n.], 1972: 449-473. |
| [6] | ACAR A, YLVDEMIR MT, AKYILMAZ O, et al. Deformation Analysis with Total Least Squares[J]. Natural Hazards and Earth System Sciences, 2006, 6: 663-669. |
| [7] | FELUS F, BURTCH R. On Symmetrical Three-dimensional Datum Conversion[J]. GPS Solutions, 2009, 13(1):65-74. |
| [8] | AKYILMAZ O. Solution of the Heteroscedastic Datum Transformation Problem[R]. Munich: International Association of Geodesy, 2012. |
| [9] | LU Jue, CHEN Yi, FANG Xing, et al. Performing 3-D Similarity Transformation Using the Weighted Total Least-squares Method[R]. Munich: International Association of Geodesy, 2012. |
| [10] | NEITZEL F. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12):751-762. |
| [11] | LI Bofeng, SHEN Yunzhong, LI Weixiao. The Seamless Model for Three-dimensional Datum Transformation[J]. Science China: Earth Science, 2012, 55 (12): 2099-2108. |
| [12] | LI Bofeng, SHEN Yunzhong, ZHANG Xingfu, et al. Seamless Multivariate Affine Error-in-variables Transformation and Its Application to Map Rectification[J]. International Journal of Information Science, 2013, 27(8): 1572-1592. |
| [13] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722. (陈义,陆珏.以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报,2012,41(5):715-722.) |
| [14] | LU Jue, CHEN Yi, ZHENG Bo. Applying Total Least Squares to the Three-dimensional Datum Transformation[J]. Journal of Geodesy and Geodynamics, 2008, 28(5):77-81. (陆珏, 陈义, 郑波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2008, 28(5): 77-81.) |
| [15] | XU Chaoqian, YAO Yibin, XIONG Siting, et al. 3D Rectangular Coordinate Transformation Adapted to Arbitrary Rotation Angle Based on Total Least-Squares Regression[J]. Journal of Geomatics, 2010, 35(5): 46-48. (许超钤,姚宜斌,熊思婷,等. 三维任意旋转角度坐标转换的整体最小二乘回归解法[J]. 测绘信息与工程,2010, 35(5):46-48.) |
| [16] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. |
| [17] | FANG Xing. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [18] | GE Xuming, WU Jicang. Iterative Method of Weight Constraint Total Least Squares for Three Dimensional Datum Transfor-mation[J]. Science of Wuhan University:Geomatics and Information, 2012, 37(2): 178-182. (葛旭明,伍吉仓. 三维基准转换的约束加权混合整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版,2012, 37(2):178-182.) |
| [19] | NOCEDAL J, WRIGHT S. Numerical Optimization[M]. Berlin: Springer, 2006. |
| [20] | LENZMANN L, LENZMANN E. Zur Lsung des Nichtlinearen Gauss-Markov-Modells[J]. Zeitschrift für Geodsie, Geoinformation und Landmanagement, 2007, 132: 108-120. |
| [21] | KONG Jian, YAO Yibin, WU Han. Iterative Method for Total Least-squares[J]. Science of Wuhan University:Geomatics and Information, 2010, 35(6): 711-714. (孔建,姚宜斌,吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版,2010,35(6):711-714.) |
| [22] | SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations: Three Algorithms[J]. Journal of Geodesy, 2008, 82(6):373-383. |
| [23] | CAI Jianqing, GRAFAREND EW. Systematical Analysis of the Transformation between Gauss-Krueger-coordinate/DHDN and UTM-coordinate/ETRS89 in Baden-Württemberg with Different Estimation Methods[C]//Geodetic Reference Frame International Association of Geodesy Symposia. Munich: International Association of Geodesy, 2009, 134:205-211. |