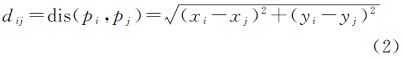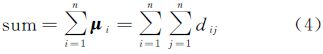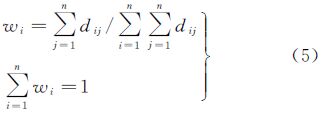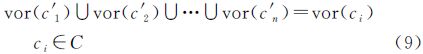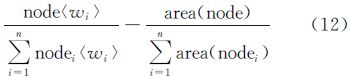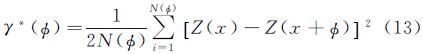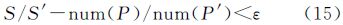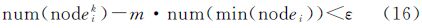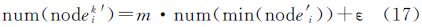1 引 言
点群综合的目的是在点数目减少的情况下尽量正确表达点群的整体信息,即采用一定的模型或算法从原始的点群中抽取出含有一定数量点的子集合。当制图对象的质量、数量特征过于详细时,就要采取聚类和扩差措施进行概括,减少其质量和数量特征的差别,以达到地物类别清楚、层次分明的效果[1]。
许多学者对点群目标的综合选取进行了不同方法的试验与研究。目前,基本方法是首先对点的重要性进行判断,然后以取舍方式进行点群综合。该方法存在一定的弊端,例如点状居民地选取算法不能很好地处理拓扑信息,而基于Voronoi图的综合算法又没有考虑到点的重要性程度[2, 3, 4, 5, 6, 7]。基于以上考虑,本文结合聚类方法提取聚类中心点,并用层次Voronoi图结构逐步细化地表达聚类中心点,进而实现点群由繁到简综合。通过采取逐层次的聚类中心点概括,更加便于点群分布表达与拓扑几何信息计算,而且可以有效实现类簇点的图形化,优化点群综合过程。
2 层次Voronoi图 2.1 空间点群权重值分配空间点的权重值反映了该空间点在空间点群整体中的个体重要程度。集合P={p1,p2,…,pn}代表二维空间的点群整体,其中,空间点pi∈P描述为平面坐标(xi,yi)形式。集合P中共有n个空间点,采用欧氏距离作为权重度量确定点群中各点的权重值[8]。使用n×n形式的距离矩阵D表达空间点群中点之间的距离关系
距离矩阵D是对角线元素为0的对称矩阵,即D=DT,dii=0,dij=dji。其中dij表示点pi到点pj的欧氏距离。dis(·)为欧氏距离算子,dij计算如式(2) 点pi与点群P中各点的距离之和等价于行向量μi的各元素之和 根据式(3),点群P中各点之间所构成的距离总和为 以点pi距离和与点群P的距离总和之比为权重,点pi的权重值wi描述为式(5) 此处,因各点的权重值均为与点群P的距离总和之比,所以,满足归一化条件,即各点权重值之和为1。 2.2 空间点群聚类点群聚类将点群划分为簇(cluster)的过程,使得位于不同簇中的点之间差别较大,而处于同一簇中的点之间具有较小的差异。点群聚类算法多数是以距离为基础的簇识别过程,最为典型的是k-means算法[9]。本文采用戴维斯·鲍尔丁指数(Davies Bouldin index,DBI)[10]来判定当前聚类结果是否达到最优。DBI指数的物理意义是簇内之间距离之和与簇外之间距离之比,能够有效地使k-means算法得到整体最优解。空间点群聚类算法过程如下:
输入:空间点群集合P。
输出:空间类簇集合R。
(1) 对于任意∀pi∈P,根据式(1)计算距离矩阵D并得出行向量μi,将行向量μi的元素按降序排列,取前两个值与其对应的两个点p1、p2,作为初始聚类中心o1←p1、o2←p2,并将聚类中心置于数组clusterArray←o1、o2。
(2) 根据式(2),对于任意∀pi∈P,∀oi∈clusterArray,分别计算出pi到元素oi的距离值,并以到聚类中心的距离最小为原则,将pi分类,标记类别,并置于数组classArray←pi。
(3) 根据文献[10],计算此时的classArray中的类簇最大相似度均值,置于currIndex。
(4) 遍历数组classArray:① 根据式(2),计算pi至各聚类中心的最小距离,并构成序列O(min(dis(o1,pi),dis(o2,pi),…,dis(on,pi));② 取O中的最大值及其相关点oi。
(5) 计算classArray中的类簇最大相似度均值,置于newIndex。
(6) 如果currIndex<newIndex,将距离clusterArray中各聚类点最远的数据点oi置入clusterArray,clusterArray←oi,返回至步骤(2)。
(7) 如果currIndex≥newIndex,根据式(5),计算各聚类中心点的权重值,输出聚类结果集R。
(8) 算法结束。
2.3 空间点群的层次Voronoi图用Voronoi图数据结构进行空间点群的二维空间剖分。首先,点的Voronoi子区域为点的凸域(convex domain)表达,并且点与其凸域之间为一一对应关系;其次,Voronoi图是一种无缝隙无重叠的连续空间覆盖,可以消除层次结构边界的二义性;第三,可避免长、宽比率过高的子区域出现,能够更好地真实表达点群在空间上的形态分布。
定义1:普通Voronoi图[11, 12]。点群P={p1,p2,…,pn}(2≤n<∞,pi≠pj),对于pi(xi,yi)∈P,式(6)描述pi的Voronoi子区域
dis(·)为欧氏距离算子,同式(2)。由式(7)描述的图形结构称为点群P的普通Voronoi图以点群聚类中心为支撑,可以有效地刻画点群层次性,即每一层次的聚类中心点可顺序地构成点群由总体粗略至局部细致的表达。以每一层聚类中心点构成的普通Voronoi图为基础,存在某一层次聚类中心点群C,并且,由C构成普通Voronoi图,vor(C)={vor(c1),vor(c2),…,vor(cn)}。设每个聚类中心点的Voronoi子区域内存在聚类中心点群C′。给出层次Voronoi图的定义如下。
定义2:层次Voronoi图。存在上下连续两层次的聚类中心点群C与C′,对于∀c′1,c′2,…,c′n∈C′,如果满足
则称由下式表达图形结构称为C与C′共同构成的层次Voronoi图定义2中,式(8)说明上层某一聚类中心的Voronoi子区域包含下层聚类中心点群。与此同时,式(9)说明下层聚类中心点群的Voronoi子区域的并集等价于它们所对应的上层聚类中心点的Voronoi子区域。引入加权重距离(additively weighted distance,AWD)[13, 14, 15]进一步描述聚类中心点的Voronoi子区域
式中,ci为某一聚类中心点;wi为根据式(8)得到ci的类簇权重值,即ci的Voronoi子区域所包含的下一层次聚类中心点的权重值之和。普通Voronoi图(实心点群)与权重Voronoi图(空心点群)的示例,如图 1所示。

|
| 图 1 普通Voronoi图与权重Voronoi图 Fig. 1 Ordinary Voronoi diagram and weighted Voronoi diagram |
将每一层次的聚类中心点集合C表达为普通Voronoi图数据结构,进而将其描述为树结构的结点,结点的数据结构描述如下:
structure treeNode
{
point _center;
polygon _regions;
integer _lev;
double _wt;
double _dis;
double _rad;
treeNodeArray _childs;
}
其中,_center为二维点类型〈id,x,y〉,用于存储当前的聚类中心点;_regions为二维面类型〈id,pointArray〉,用于存储聚类中心点的Voronoi子区域;_lev描述当前层节点位于树结构中的层次;_wt记录当前节点的权重值;_dis记录当前结点与其父节点的距离值;_rad记录当前节点与其父节点的角度值;_childs代表当前节点的叶子节点,为treeNode类型的数组。根据以上定义与树结构结点描述,层次权重Voronoi图可描述为层次Voronoi图树结构(Voronoi hierarchical tree,VHT),如图 2所示。需要说明的是,鉴于点群在空间分布上的不均匀性,VHT树结构整体表现为非平衡多叉树(non-balanced and multi-way tree)形式,即处于树结构同一层中的结点所包含的孩子节点数不相同,并且,各叶子结点的层数不相同。

|
| 图 2 层次Voronoi图的树结构 Fig. 2 Tree of hierarchical Voronoi diagram |
点群是空间分布分析的主要对象,点群分布的定量特征主要由分布范围、排列方式和密度3个方面决定[16, 17, 18, 19, 20]。
3.1 分布范围(scope)由于空间点群分布的不规则性,需要一种能够根据点群的分布特点来实现点群分布范围表达的图形结构。根据上述基于聚类的权重层次Voronoi图结构,能够有效地描述点群分布趋势。在VHT树中,以父节点的权重值表示该点群的分布范围,通过权重Voronoi图将其分布范围以区域面积大小的形式表达并计算。设VHT树结构的当前层存在n个结点,并且当前结点为node,那么,node的分布范围大小由下式计算
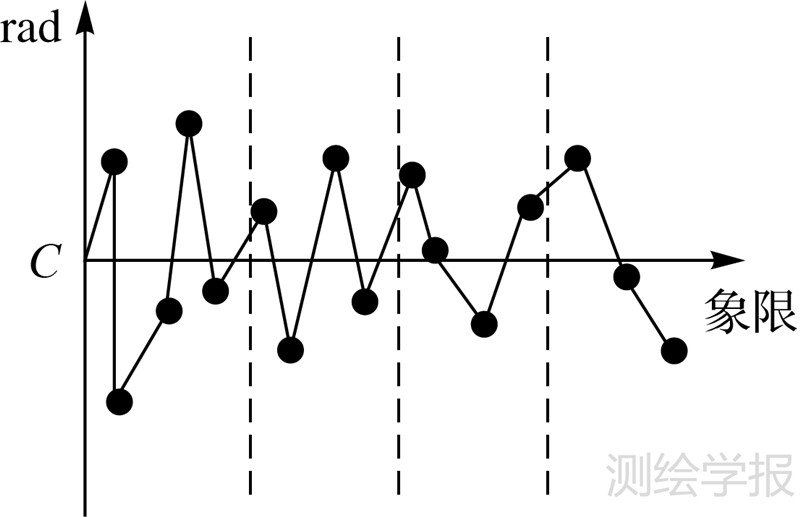
式中,node〈wi〉为当前结点的权重值;area(node)为当前结点的权重Voronoi子区域面积值。 3.2 排列方式(arrangement)以正北方向为标准方向,按顺时针顺序,以父节点C为中心,其子节点与父节点的相对象限位置为横轴,子节点与父节点的相对方位角度为纵轴,抽象表达出点群的排列方式,如图 3—图 5所示。
|
| 图 3 环状排列 Fig. 3 Circular arrangement |
|
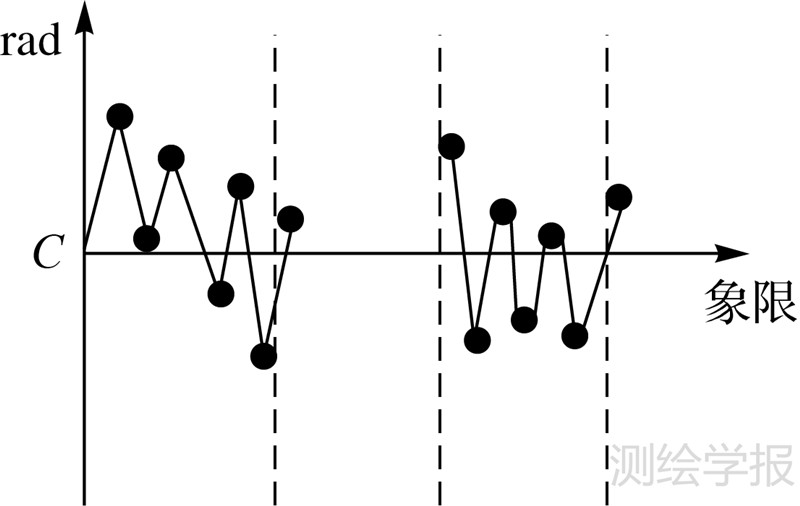
| 图 4 条带状排列 Fig. 4 Banded arrangement |
|
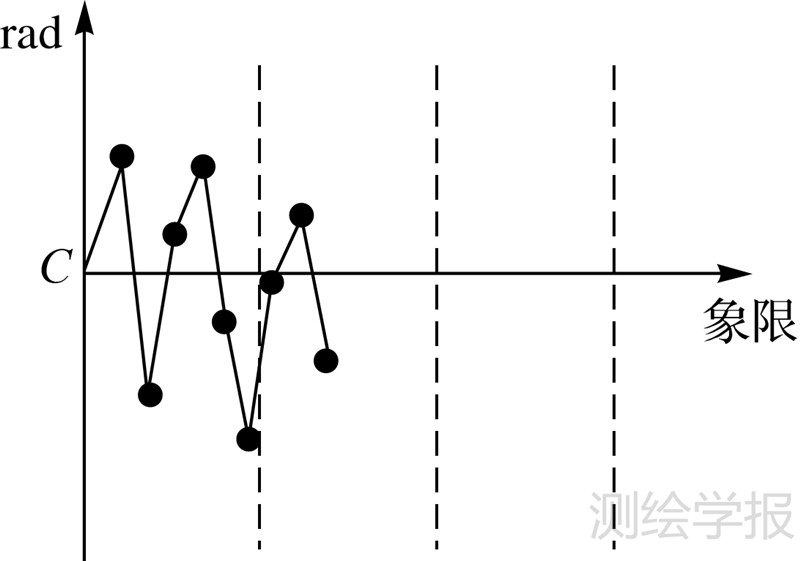
| 图 5 块状排列 Fig. 5 Massive arrangement |
从描绘的曲线图中可得出,图 3在整个象限上弧度值均有分配,全局上呈现出连续分布,据此推断出此点群的排列方式为中心环状分布。如果弧度值的分配集中于象限的两端,即弧度值在各自的象限边界处连续,如图 4所示,则此点群为按条带状分布排列。若点群的弧度值在整体范围内的某一局部区域内连续,则点群是按块状方式排列,如图 5所示。
通过点群方向的变差函数(γ*),可确定点群的排列方式以及空间点群间的拓扑邻近性
式中,φ为角度参数;Z(x)与Z(x+φ)为区域化变量;N(φ)为点对数目。在层次权重Voronoi图中应用自适应聚类算法,可以确定点群类簇点的排列方式,进而确定其内部点的排列方式。通过聚类运算获得的类簇点坐标确定相对的位置和方向、通过构造的点群拓扑包含关系可确定点之间的拓扑关系。
3.3 密度控制(density)点群综合的整体性特征要求是,在点群密集的区域综合后仍然保持相对密集,而稀疏区域仍然保持相对的稀疏。相对于VHT树的根节点,取树结构第2层中的最小权重值节点min(nodei)为基准,统计其Voronoi子区域中包含的点目标个数num,计算如下
式中,vor为结点的Voronoi子区域边界所包含的点;nodei(·)为结点Voronoi区域子区域范围所包含的点。考虑综合前后比例尺的变化,该节点下的综合目标点个数num(P′)需满足以下条件 式中,S为原始比例尺;S′为综合比例尺。根据该结点所包含的综合节点总数,计算该结点分支下需要剖分的层次数,即决定结点分枝树的层数。该层次中的其他节点与该最小权重值节点需满足以下条件 式中,min(·)代表层次中面积最小的Voronoi子区域。确定其节点的点群目标综合后的数据点个数相对于最小节点综合数据点的倍数 根据m值,进而确定其分支树的层次,以保证综合后的密度疏密程度和原始数据相一致。在式(16)与式(17)中,nodeik为根节点下第k个权重子节点;m为当前层中面积最小的Voronoi子区域所包含的聚类中心数与当前层聚类中心点数之比;num(nodeik)为结点nodei的Voronoi子区域所包含的数据点个数;num(nodeik′)为点群综合后结点nodei的Voronoi子区包含的数据点个数。 4 算例与分析算例由空间点群聚类、层次加权Voronoi图构建、VHT树构建与点群综合方法4个部分构成,相关数据结构与算法在Visual Studio 2010 C#、ESRI ArcGIS Engine 10环境实现。根据给定的点群数据,首先得到点群的最小外接矩形(minimum boundary rectangle,MBR)代表计算域,由聚类的类簇点建立权重Voronoi图,并在每个权重Voronoi图形中顺次调用聚类算法、权重点的层次Voronoi图剖分方法,建立VHT树结构,进而实现空间点群的不同层次综合。
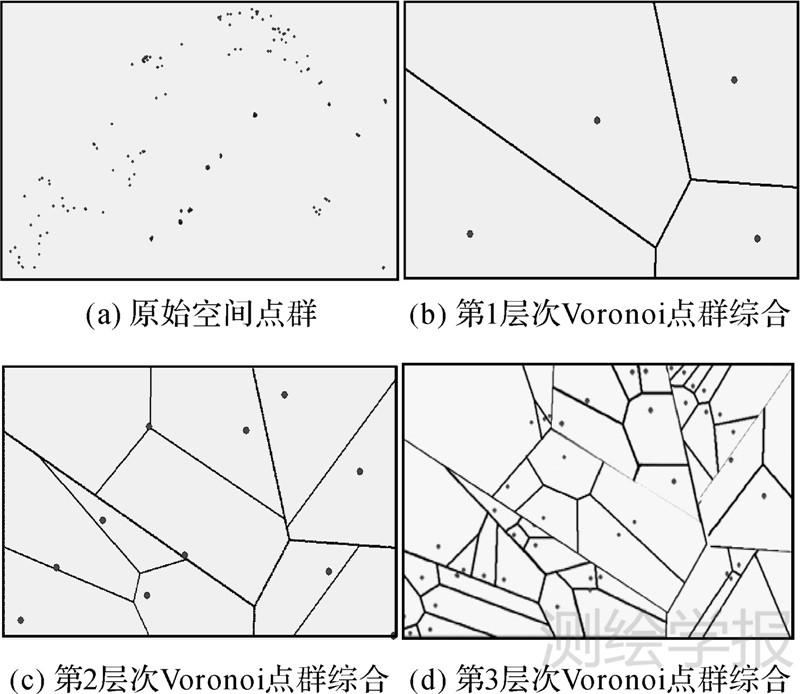
如图 6所示,图 6(a)为1∶50 000比例尺云南省腾冲市居民地点群目标数据,共计1000个数据点;图 6(b)为第1次点群聚类与权重Voronoi图剖分结果,可以看出点群分布由4个聚类中心点表示;图 6(c)为对每个权重Voronoi子区域进行再次聚类、剖分,每个子区域内点数量增加,此时,由第1次的4个聚类中心点扩展到11个聚类中心点,由于具有层次性,因此,这11个点分别代表点群在4个Voronoi子区域内的分布趋势;图 6(d)是第3次Voronoi综合后的结果,可以看出,点群在第3层次被细化表达为49个聚类中心,且是第2层11个Voronoi子区域的细化,聚类中心与原始点群在点密度上、分布上趋于一致。
|
| 图 6 层次Voronoi图的点群综合过程 Fig. 6 Process of point group generalization based on hierarchical Voronoi |
多数地理现象都具有空间相关特性,即距离越近的两事物越相似。在实际应用中,各向异性现象表现更为普遍,即将方向因素纳入考虑范畴时,有可能在某个方向距离更远的事物存在更大的相似性,这种现象被称为半变异和协方差分析中的方向效应。
如图 7—图 9所示,以提取出数据的东北—西南方向为例,获得点群对的半变异云图(semivariogram/covariance cloud),其中纵坐标γ为变异函数值,横坐标h为点对之间的距离。

|
| 图 7 第1次提取的半变异点对云图 Fig. 7 The first covariance cloud |

|
| 图 8 第2次提取的半变异点对云图 Fig. 8 The second covariance cloud |

|
| 图 9 第3次提取的半变异点对云图 Fig. 9 The third covariance cloud |
点群的范围、排列、密度与几何均值的参数统计如表 1所示。
| 点 群 | 范 围 | 排 列 | 密 度 | 几何均值 |
| 图 6(b) | 0.90 | 0.142 | 0.152 | 0.267 |
| 图 6(c) | 0.94 | 0.381 | 0.208 | 0.421 |
| 图 6(d) | 0.98 | 0.447 | 0.728 | 0.683 |
试验表明,随着剖分层次的递增,对点群的表达会越来越详细。据此,可针对不同比例尺地图和实际需求提取不同程度的点群综合图,获得满足需求的比例尺地图要素,避免点取舍过程的繁琐判断。
5 结 论本文通过在层次Voronoi图中应用本文的自适应聚类算法,实现了空间点群目标的制图综合。该方法不仅无需获得点群中点的重要性先验知识,而且可以表现出点群的空间范围特征、点群的空间排列,以及点群在不同概括程度上的分布状况。但具体的综合要求、算法精度以及不同类型空间目标之间的协调一致等问题还有待于作进一步的研究。此外,层次Voronoi图亦可作为空间索引与空间数据可视化的基础数据结构,如何构建多路平衡形式VHT树是非常值得关注的问题。
| [1] | MA Yongli. Cartography Course[M]. Nanjing: Nanjing University Press,2003. (马永立. 地图学教程[M]. 南京: 南京大学出版社, 2003.) |
| [2] | YU Yanping, SHEN Jie, SHANG Zaiying. A Study on the Time Complexity of Point Cluster Selection and Simplification Algorithms[J]. Journal of Nanjing Normal University: Natural Science Edition, 2012, 35(1): 111-116. (于艳平,沈婕,尚在颖. 点群选取与化简算法时间复杂度研究[J]. 南京师范大学报: 自然科学版, 2012, 35(1): 111-116.) |
| [3] | WANG Jiayao, DENG Hongyan. A Model of Cartographical Generalization Based on Genetic Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(7): 565-569. (王家耀,邓红艳. 基于遗传算法的制图综合模型研究[J]. 武汉大学学报: 信息科学版, 2005, 30(7): 565-569.) |
| [4] | QIAN Haizong, WU Fang, ZHANG Linlin, et al. Quality Assessment of Point Group Geometry Generalization with Polarization Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(4): 261-269. (钱海忠,武芳,张琳琳,等. 基于极化变换的点群综合几何质量评估[J]. 测绘学报,2005, 34(4): 261-269.) |
| [5] | LU Yi, ZHAI Jingsheng, DU Jinghai, et al. Recognition, Measurement and Generalization for Point Cluster Features in Digital Nautical Chart[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2): 133-139. (陆毅,翟京生,杜景海,等. 数字海图点群状特征的识别、量测与综合[J]. 武汉大学学报: 信息科学版,2001, 26(2): 133-139.) |
| [6] | GUO Qingsheng. Structuralizing Point Features and Its’s Application in Map Generalization[J]. Journal of the PLA Institute of Surveying and Mapping, 1999, 16(3): 210-213. (郭庆胜. 点状要素群的结构化及其在综合中的应用[J]. 解放军测绘学院学报,1999, 16(3): 210-213.) |
| [7] | AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 175-181. (艾延华,刘耀林. 保持空间分布特征的群点化简方法[J]. 测绘学报, 2002, 31(2): 175-181.) |
| [8] | ELENA D, MICHEL M D. Encyclopedia of Distance[M]. [S. l]: Luthaze Press, 2009. |
| [9] | GUO Qingsheng, ZHENG Chunyan, HU Huake. Hierarchical Clustering Method of Group of Points Based on the Neighborhood Graph[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 256-261. (郭庆胜,郑春燕,胡华科. 基于邻近图的点群层次聚类方法的研究[J]. 测绘学报, 2008, 37(2): 256-261.) |
| [10] | DAVIES D L, BOULDIN D W. A Cluster Separation Measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 224-227. |
| [11] | CHEN Jun. Voronoi-based Dynamic Spatial Data Model[M]. Beijing: Surveying and Mapping Press, 2002. (陈军. Voronoi动态空间数据模型[M]. 北京: 测绘出版社, 2002.) |
| [12] | ZHAO Renliang. Voronoi Methods for Computing Spatial Relations in GIS[M]. Beijing: Surveying and Mapping Press, 2006. (赵仁亮. 基于Voronoi图的GIS空间关系计算[M]. 北京: 测绘出版社, 2006.) |
| [13] | BALZER M, DEUSSEN O. Voronoi Treemaps[C]// IEEE Symposium on Information Visualization 2005: INFOVIS. New York: IEEE, 2005: 49-56. |
| [14] | DONG P L. Generating and Updating Multiplicatively Weighted Voronoi Diagrams for Point, Line and Polygon Features in GIS[J]. Computers & Geosciences, 2008, 34(4): 411-421. |
| [15] | AURENHAMMER F, EDELSBRUNNER H. An Optimal Algorithm for Constructing the Weighted Voronoi Diagram in the Plane [J]. Pattern Recognition, 1984, 17(2): 251-257. |
| [16] | LIU Tao, DU Qingyun, YAN Haowen. Spatial Similarity Assessment of Point Clusters[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1149-1153. (刘涛,杜清运,闫浩文. 空间点群目标相似度计算[J]. 武汉大学学报: 信息科学版, 2011, 36(10): 1149-1153.) |
| [17] | BONAN L, FREDERICO F. TDD: A Comprehensive Model for Qualitative Spatial Similarity Assessment [J]. Spatial Cognition and Computation, 2006, 6(1): 31-62. |
| [18] | CAI Y X, GUO Q S. Point Set Generalization Based on the Kohonet Net[J]. Geo-spatial Information Science, 2008, 11(3): 221-227. |
| [19] | LI Yulong, ZHU Huahua. Automated Recognition of Point Cluster Scope with Voronoi Diagram[J]. Journal of Engineering Graphics, 2007, 28(3): 73-77. (李玉龙,朱华华. 应用Voronoi图的点群范围自动识别[J]. 工程图学学报, 2007, 28(3): 73-77.) |
| [20] | PATRICIA F, RAY L, JOHN R. A Comparison of Geometric Approaches to Assessing Spatial Similarity for GIR [J]. International Journal of Geographical Information Science, 2008, 22(3): 337-360. |