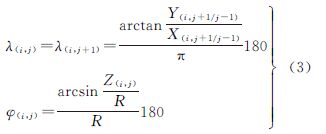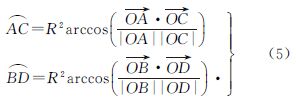2. 江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application,Nanjing 210023,China
1 引 言
全球离散格网(discrete global gird,DGG)主要研究如何将地球表面剖分成一个等面积、等形状、具有多分辨率的空间层次格网结构[1],采用每个格网对应的地址码代替地理坐标在球面上进行操作。由于地址码既表示位置,又表达了比例尺和精度,因此已被广泛应用于全球尺度空间数据集成与模式计算中[2, 3]。最常见的DGG构建方法是以经纬弧线为基础,使得基于经纬坐标系的数据及算法无需进行坐标变换即可使用,但该格网存在单元面积从赤道向南北两极逐渐收敛造成格网粒度不均匀以及极点收敛等问题[4]。另一类常见的DGG构建方法是基于5种基本柏拉图立体,目前研究较多的是基于正八面体或正二十面体的球面三角形离散格网[5, 6]、球面菱形离散格网[7, 8]与球面六边形离散格网[9, 10]。该类DGG因具有粒度近似多层次多分辨率等特性,目前成为研究的重点。
球面菱形离散格网具有类似于平面正方形格网的几何结构,在剖分方法与编码机制上比三角形或六边形格网简单,且具有方向性一致、径向对称和平移相和性,易于实现邻近搜索和层次关联等空间操作,适应于全球空间数据管理与模式计算[11]。正八面体6个顶点可以定位在两个极点和4个等分的赤道点上,任意的经纬度坐标能很容易地定位到其中一个面上[12]。相关学者对球面菱形离散格网正八面体剖分方法、编码模型、空间数据建模以及空间分析等方面均进行了较为深入的研究[5, 7, 8]。然而,正八面体的形状与球体相差较大,因此格网系统的单元形状会出现较大变形(图 1)。相比之下,正二十面体是最接近球面的柏拉图立体[12],基于正二十面体所构建的DGG将具有更均匀的几何性质,有利于全球空间数据建模与模式模拟[13],因此逐步引起相关研究者的关注[14, 15, 16]。

|
| 图 1 正八面体和正二十面体对比 Fig. 1 Comparison between octahedron and icosahedron |
剖分方法是构建DGG的基础,以菱形作为基本格网单元的DGG,通常采用四叉树剖分策略[19],但正二十面体的几何性质、拓扑性质比正八面体更为复杂,无法直接采用现有的球面菱形离散格网正八面体剖分方法[5, 7, 8]。
2 正二十面体与球面的对应关系球面菱形离散格网正二十面体剖分首先要确定正二十面体各个顶点在球面上的位置。文献[17]分别在两极各放置一个顶点,其中一条通过北极的边线和0°经线重合(图 2(a))。图 2(b)、(c)将大部分多面体顶点放在海洋上,减少顶点对陆地数据的影响[16, 17, 18]。地理现象客观存在着水平地带性特征(即经度地带性和纬度地带性的合称),同时地球是以南北两极所确定的地轴为中心进行自转。后一种放置方法只能针对陆地应用,且没能顾及地球的自转特性。因此本文采用文献[17]提出的方法建立正二十面体与球面的对应关系。将正二十面体中顶点位于极点处的三角形与其极点对边相邻的三角形进行合并,可以将正二十面体划为10个初始菱形格网单元。这些格网单元沿赤道对称,符合地球南北两极的方向性、对称性和水平地带性特征,便于后续的剖分、编码与地理坐标转换。
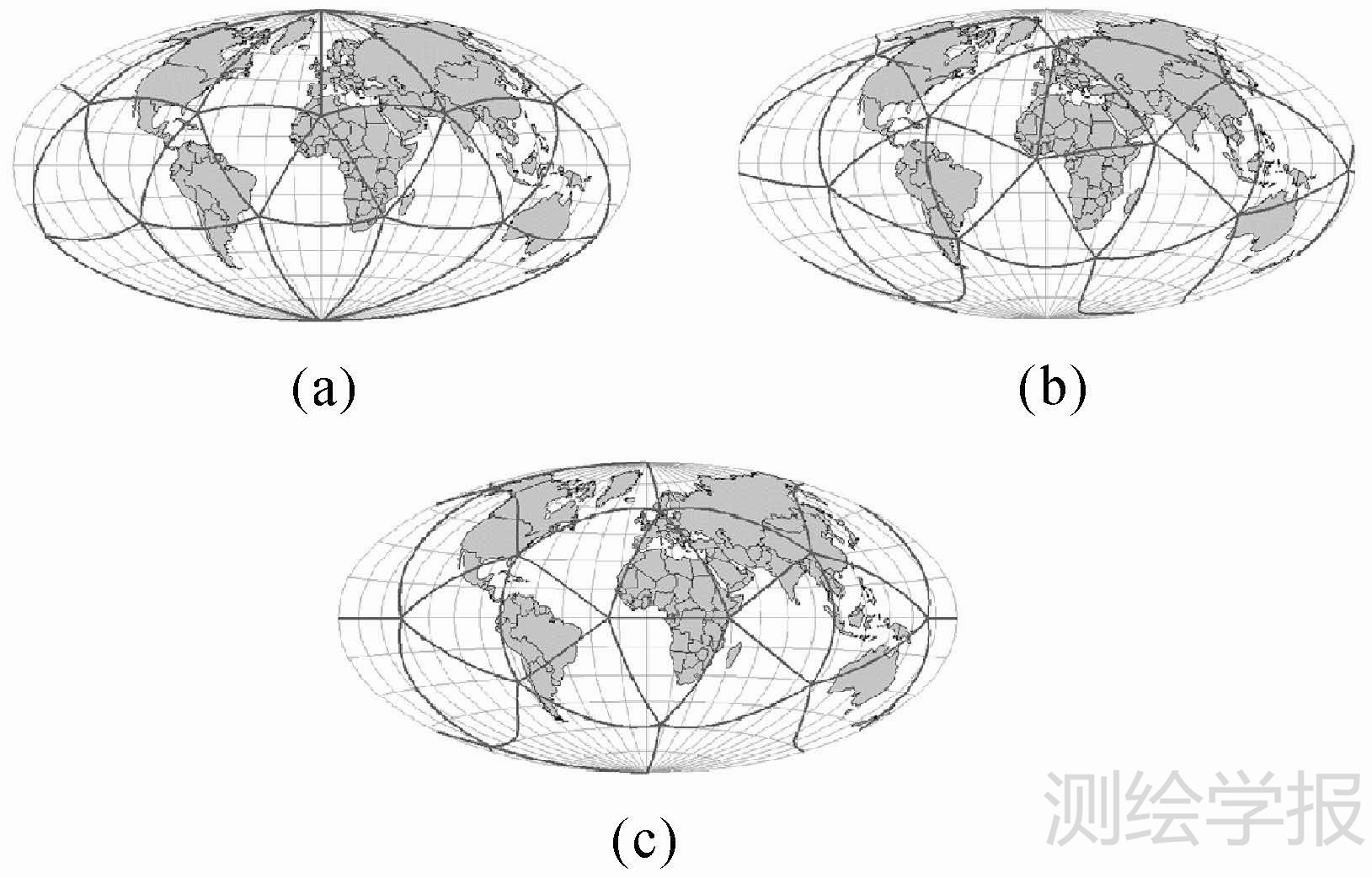
|
| 图 2 正二十面体的3种不同放置方法 Fig. 2 Icosahedron placed in three different ways |
初始菱形格网单元确定后,即可进行格网单元的层次递归剖分。球面菱形离散格网单元形状、大小近似规则、均匀,拓扑连接关系类似于正方形格网,可以按照四叉树或其他方式进行层次递归剖分[19]。正二十面体结构的复杂性以及南北两极处的极点奇异性给格网单元与球面经纬度的转换带来问题。分析发现,球面菱形离散格网单元的几何位置既可以用经纬坐标表达,也可以由以球心为原点的三维直角坐标表达,且在三维直角坐标系中不存在极点收敛,有利于实现球面菱形离散格网的层次递归剖分。
3.1 球面经纬度坐标与三维直角坐标的相互转换 3.1.1 球面经纬度坐标向三维直角坐标转换设地球半径为R,格网点(i,j)的经纬度坐标分别为G(i,j)=(λ(i,j),φ(i,j)),对应的空间直角坐标为C(i,j)=(X(i,j),Y(i,j),Z(i,j)),借助空间几何关系即可建立从球面经纬度坐标向三维直角坐标的坐标转换关系如下
3.1.2三维直角坐标向球面经纬度坐标转换球面格网点的三维直角坐标向球面经纬度坐标转换,是将一个不收敛空间转换到一个收敛空间。对于非极点处(即Z(i,j)=R,-R),可基于式(2)建立转换关系。地球南北两极处(当Z(i,j)=R或-R时),极点奇异性带来一对多的映射冲突,但与极点同属于一条格边的另一格点并不存在映射冲突的问题,且这两个格点处在同一条经线上,即λ(i,j+1)=λ(i,j),可基于式(3)建立转换关系
3.2 格网单元层次递归剖分算法基于球面经纬度坐标与三维直角坐标的相互转换关系,进行球面菱形离散格网层次递归剖分,算法主要步骤包括(图 3):①根据正二十面体与球面的对应关系,确定初始菱形格网的球面经纬坐标;②将初始菱形格网从球面经纬坐标映射为三维直角坐标,根据剖分层次,采用大圆弧平分方法进行层次递归剖分,建立剖分层级与对应比例尺的关系(表 1);③将剖分结果从三维直角坐标转换至球面经纬度坐标。

|
| 图 3 基于正二十面体的球面菱形离散格网层次递归剖分算法流程 Fig. 3 The recursive subdivision algorithms flow of spherical diamond discrete grids based on icosahedron |
| 剖分层次 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 菱形边长/m | 5000 | 2000 | 1000 | 610 | 305 | 153 | 76 |
| 对应比例尺 | 1∶1000万 | 1∶500万 | 无 | 1∶100万 | 1∶50万 | 1∶25万 | 1∶10万 |
| 剖分层次 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 菱形边长/m | 38 | 18 | 10 | 5 | 2 | 1 | 0.6 |
| 对应比例尺 | 1∶5万 | — | 1∶1万 | 1∶5000 | 1∶2500 | 1∶1000 | 1∶500 |
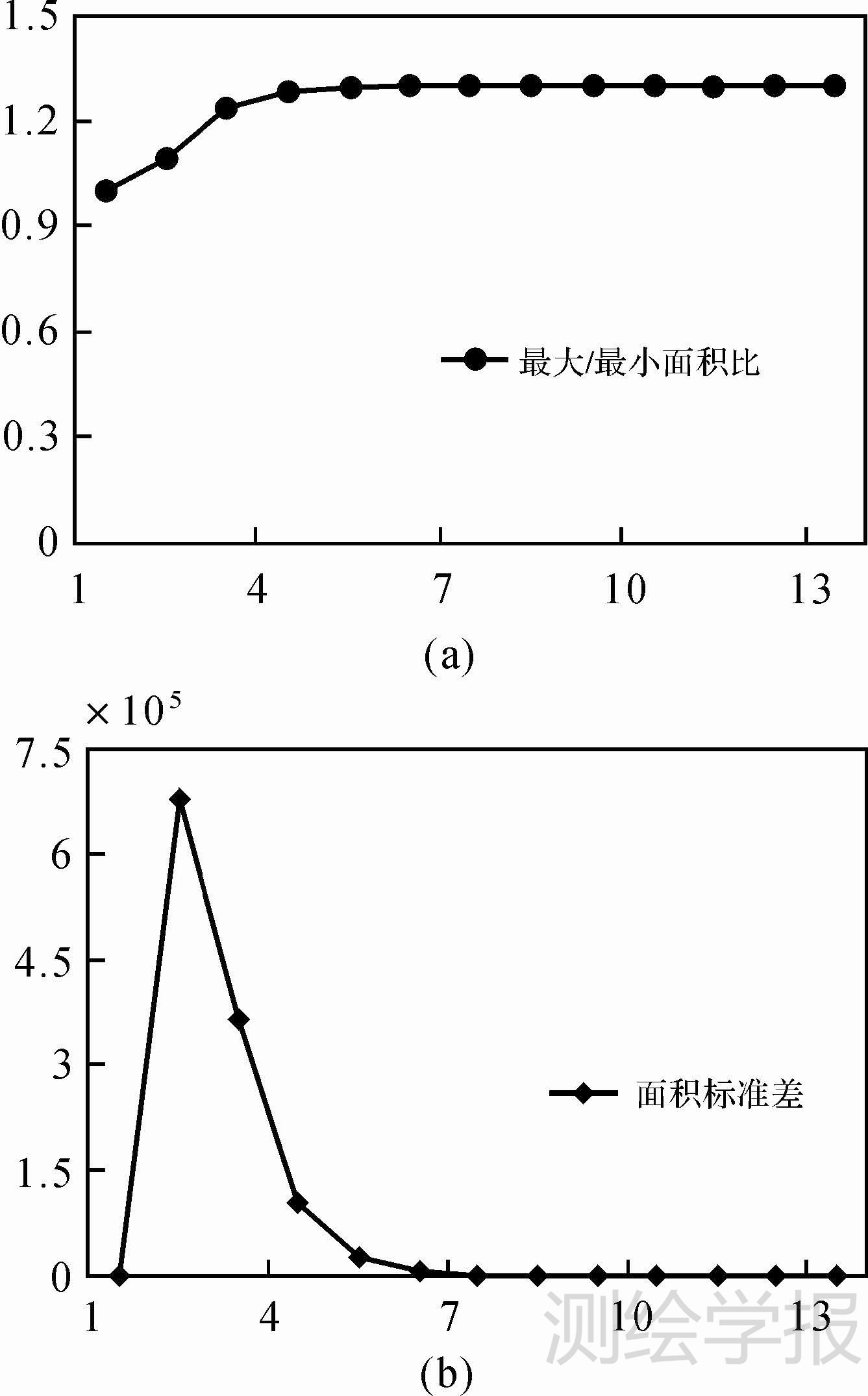
从球面几何可知,没有一种剖分方法能使球面格网在每个层次上具有像平面栅格那样完全相同的几何特征(如:面积、长度、角度),只能达到近似相等[12, 20]。目前对于球面离散格网的几何特性研究通常以对格网单元几何特性的统计分析为主[20]。下面分别从球面菱形离散格网单元面积比和标准差、长/短轴比(角度)和标准差为度量指标对本文提出的球面菱形离散格网正二十面体剖分的结果进行分析(表 2)。
| 剖分层次 | 菱形单元个数 | 单元平均面积/km2 | 最大/最小面积比 | 菱形面积标准差/km2 | 最长/最短轴比 | 轴长标准差/km |
| 0 | 4 | 49 634 416.603 000 | 1.000 00 | 1.414 210 | 1.000 00 | 0.000 |
| 1 | 16 | 15 119 046.273 801 | 1.093 67 | 676 406.815 714 | 1.891 70 | 0.222 |
| 2 | 64 | 3 994 870.800 061 | 1.237 13 | 277 371.259 458 | 2.000 00 | 0.112 |
| 3 | 256 | 1 013 025.879 161 | 1.283 75 | 79 789.155 888 | 2.051 49 | 0.056 6 |
| 4 | 1 024 | 254 164.908 250 | 1.296 32 | 21 043.726 510 | 2.065 30 | 0.028 |
| 5 | 4 096 | 63 598.228 742 | 1.299 52 | 5 384.619 700 | 2.068 82 | 0.014 |
| 6 | 16 384 | 15 903.123 306 | 1.300 33 | 1 360.777 936 | 2.069 70 | 0.007 |
| 7 | 65 536 | 3 976.003 764 | 1.300 53 | 341.970 014 | 2.069 93 | 0.003 |
| 8 | 262 144 | 994.014 875 | 1.300 58 | 85.711 176 | 2.069 98 | 0.002 |
| 9 | 104 857 | 248.504 590 | 1.300 59 | 21.454 924 | 2.069 99 | 0.001 |
| 10 | 419 430 | 62.126 202 | 1.300 60 | 5.367 109 | 2.070 00 | 0.000 |
| 11 | 16 777 216 | 15.531 554 | 1.300 60 | 1.342 199 | 2.070 00 | 0.000 |
本文采用球面大圆弧剖分方法,菱形单元的每条边均为球面大圆弧,因此菱形单元的面积等同于两个球面三角形面积之和,即SABCD=SABCD+SBCD。根据式(4)即可求得球面三角形的面积和格网单元面积的标准差
式中,∠A、∠B、∠C、∠D为菱形单元的4个顶点的内角;σ表示格网面积的标准差;Si表示每个菱形单元的面积;S表示该剖分层次下所有菱形格网的平均面积;N表示该层次下菱形单元的个数。
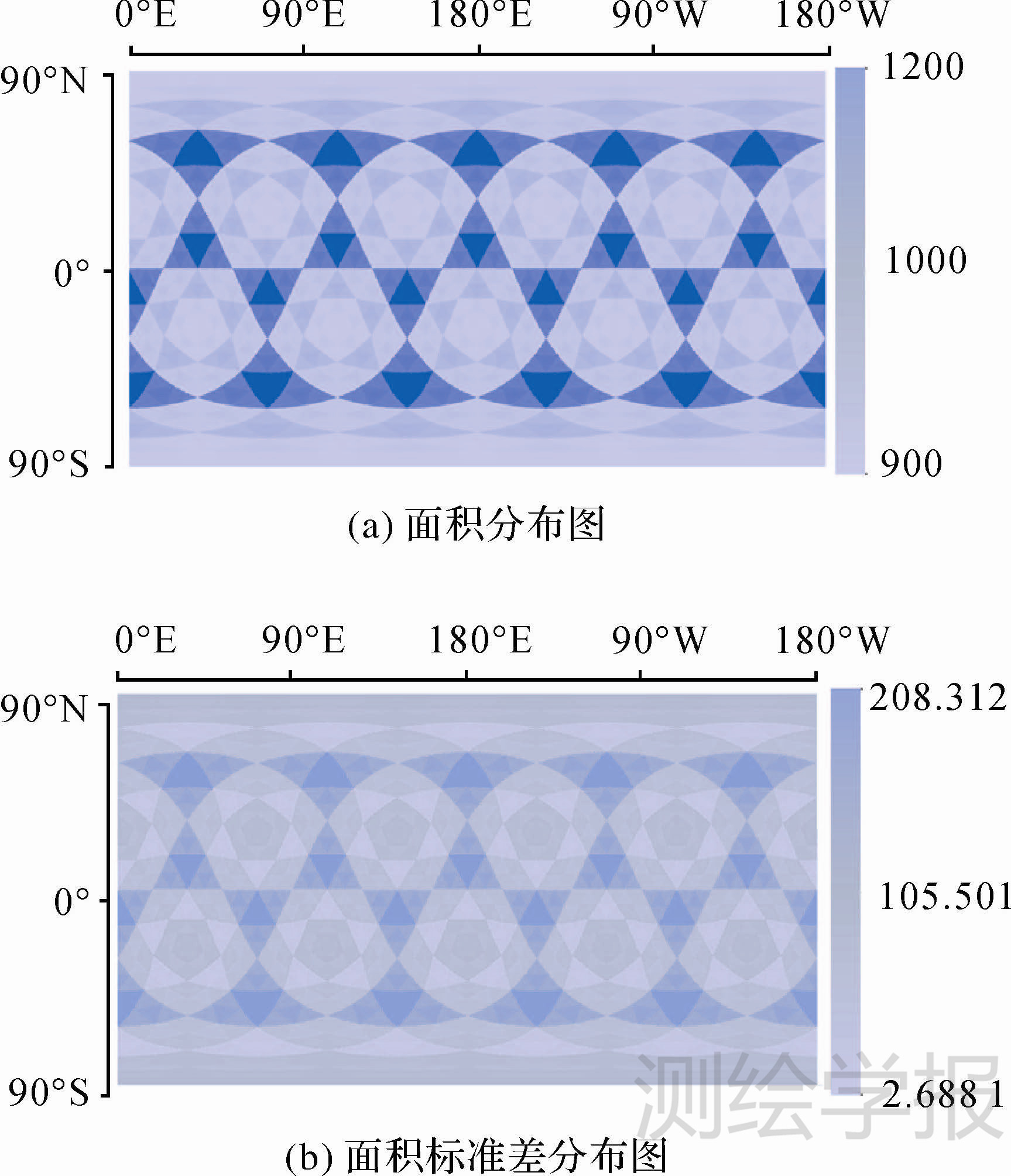
从表 2可以看出,随着剖分层次的增加,面积比首先增大然后逐渐收敛到1.3左右,标准差先增加后减,逐渐收敛到0(图 4)。说明随着剖分层次的增加,格网单元的大小能够保持近似均匀。同时,菱形单元的面积分布和面积标准差分布在初始菱形中由内到外呈现出类似于五边形的分布规律,五边形外部的菱形单元面积标准差大于内部(图 5)。
|
| 图 4 最大/最小面积比和面积标准差 Fig. 4 Max/min area ratio and area standard deviation of diamond cell |
|
| 图 5 菱形单元面积和面积标准差全球分布图 Fig. 5 The global distribution of diamond element area and the area's standard deviation |
菱形单元的长短轴之比和标准差指标的组合可以用来衡量格网单元角度变形的情况[26]。对于球面菱形的长短轴可以作如下的定义,长轴方向即为连接竖直方向上两个顶点的大圆弧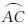 ,短轴为水平方向上两个顶点的大圆弧
,短轴为水平方向上两个顶点的大圆弧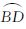 ,长轴、短轴球面长度可定义为
,长轴、短轴球面长度可定义为
式中,OA、OC、OB、OD为球心至菱形格网单元4个顶点的距离。
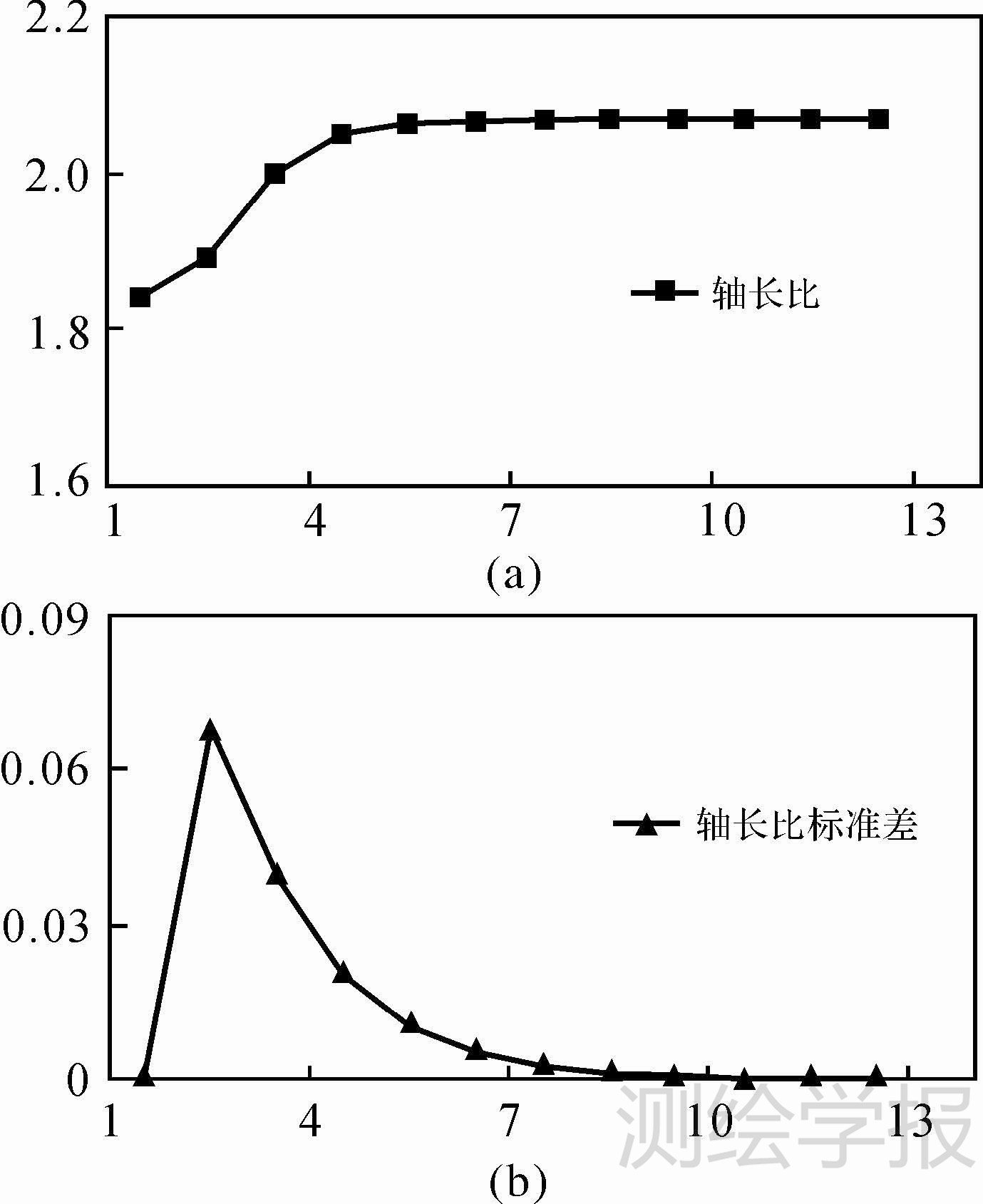
同样,从表 2可以看出,最长最短轴长比和轴长标准差表现出了与面积特性极为相似的变化的特征,即随着剖分层次的增加逐渐收敛稳定(图 6),这一特性表明随着剖分层级的增加,正二十面体格网能够保持稳定的形状变形特征。格网的形状以及面积越稳定、均匀,越有利于格网编码的实现以及数据的集成。从轴长比的分布图和轴长的分布图,可以发现:轴长比和轴长标准差的分布呈现菱形分布的特点,菱形水平方向两顶点处的变形较大;竖直方向两顶点处的变形较小(图 7)。
|
| 图 6 长短轴比和轴长标准差 Fig. 6 The axial ratio and axial standard deviation of diamond cell |

|
| 图 7 菱形单元长短轴比和长短轴比标准差全球分布图 Fig. 7 The global distribution of diamond element’s ratio of major/ minor axis and the ratio’s standard deviation |
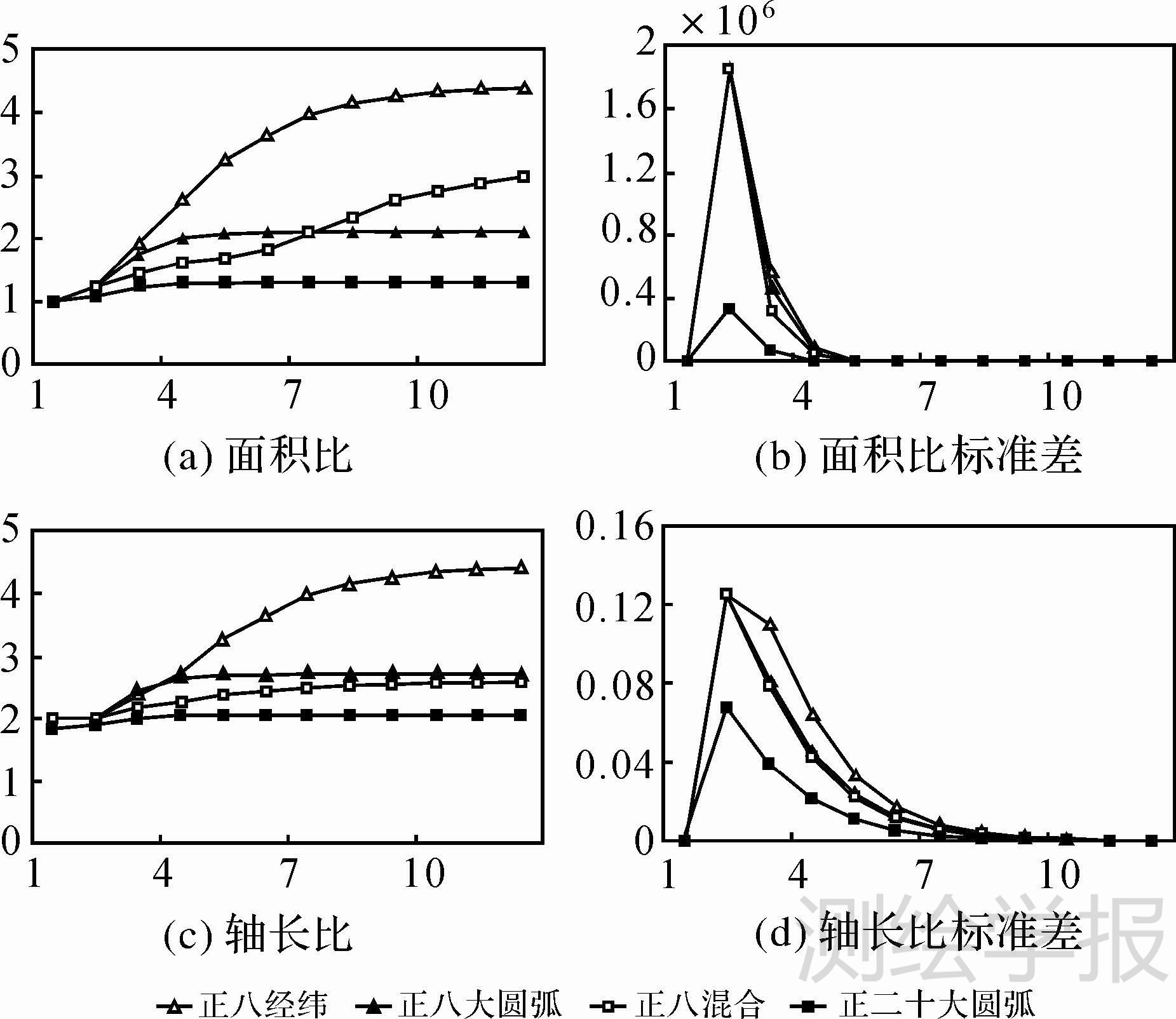
为了进一步分析基于正二十面体的球面菱形离散格网(正二十大圆弧)的几何形变性质,将其与正八面体大圆弧平分法[19](正八大圆弧法)、经纬线平分法[7](正八经纬法)以及大圆弧和经纬线混合平分法[8](正八混合法)所得到的3种球面菱形离散格网进行几何性质对比(图 8)。对比分析可以看出,基于正二十面体的球面菱形格网随着剖分层次的递增,角度变形和面积变形均保持为最小,进而表明格网的几何性质更好,更有利于空间数据集成和提高空间分析的精度。这显然是由于正二十面体相较于正八面体更加接近球面。
|
| 图 8 不同剖分方法的几何形变对比 Fig. 8 Comparisons geometry distortion between different subdivision methods |
本文在VC++ 2013环境下,基于OpenGL开发了试验系统。以90m分辨率数字高程模型SRTM数据的球面空间建模为例,将本文所提出的剖分模型与前文介绍的3种基于正八面体的球面菱形离散格网剖分模型进行效果对比(图 9)。

|
| 图 9 4种球面菱形离散格网建模效果对比 Fig. 9 Comparisions of modeling effect between four spherical diamond discrete grids |
从图 9中可以看出:正八面体大圆弧剖分方法在同一基础菱形区域内格网单元分布较均匀,但在不同区域间的格网单元面积有较明显的变化,格网整体分布不均匀(图 9(a)、(b));正八面体经纬网剖分方法在不同区域间变化非常明显,相对于正八面体大圆弧剖分方法,面积形变更大(图 9(c)、(d));正八面体混合剖分方法在同一基础菱形区域内的格网单元分布比较均匀,在不同区域间的格网单元面积有较明显的变化(图 9(e)、(f)),并且在某些区域内存在突变的情况,如图 9(f)中红色箭头所指的地方;本文剖分方法得到的格网整体分布均匀,格网单元面积形变小、排列紧致,不存在明显的形状突变(图 9(g)、(h))。对比以上4种格网的可视化效果,可以看出本文所提出的基于正二十面体的球面菱形格网在空间数据建模与集成方面具有明显的优势。
6 结论与展望本文提出了一种球面菱形离散格网正二十面体剖分法。从地球的主要地理特征出发确定正二十面体与球体的对应关系;针对南北两极处的极点奇异性,设计了收敛的球面经纬度坐标与不收敛的三维直角坐标的转换关系,实现了球面菱形离散格网的层次递归剖分与地理坐标确定;基于菱形格网单元的最大/最小面积比和面积标准差、菱形长/短轴比和轴长标准差进行了剖分单元几何变形性质的分析。分析结果表明,与现有各类球面菱形离散格网剖分方法相比,本文方法所得到的格网在不同剖分层次,角度变形和面积变形均保持为最小,具有良好的几何性质。通过数据集成实例验证,本文方法所得到的格网整体分布均匀,格网单元面积形变小、排列紧致,不存在明显的形状突变,在空间数据建模与集成方面具有明显的优势。下一步的工作是基于正二十面体菱形格网剖分模型探索菱形格网编码模型以及空间数据的表达和管理方法。
| [1] | GOODCHILD F. Discrete Global Grids: Retrospect and Prospect[J]. Geography and GeoInformation Science,2012,28(1): 1-6. |
| [2] | VINCE A. Indexing the Aperture 3 Hexagonal Discrete Global Grid[J]. Journal of Visual Communication and Image Representation,2006, 17(6): 1227-1236. |
| [3] | LAMBRECHTS J, COMBLEN R, LEGAT V, et al. Multiscale Mesh Generation on the Sphere[J].Ocean Dynamics,2008,58(3): 461-473. |
| [4] | STANIFORTH A, THUBURN J. Horizontal Grids for Global Weather and Climate Prediction Models: A Review[J]. Quarterly Journal of the Royal Meteorological Society,2012,138:1-26. |
| [5] | ZHAO Xuesheng, BAI Jianjun, WANG Zhipeng. An Adaptive Visualized Model of the Global Terrain Based on QTM[J]. Acta Geodaetica et Cartographica Sinica,2007,36(3): 316-320.(赵学胜,白建军,王志鹏.基于QTM的全球地形自适应可视化模型[J].)测绘学报,2007,36(3):316-320. |
| [6] | BAI Jianjun, SUN Wenbin, ZHAO Xuesheng.Character Analysis and Hierarchical Partition of WGS-84 Ellipsoidal Facet Based on QTM[J].Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 243-248.(白建军,孙文彬,赵学胜.基于QTM的WGS-84椭球面层次剖分及其特点分析[J].)测绘学报, 2011, 40(2): 243-248. |
| [7] | ZHANG Yumei, CHEN Weihua, NIE Hongshan, et al. Study on Sphere Rhombus Grid Recursive Subdivision[J].Geography and Geo-Information Science,2010,26(6):34-37.(张玉梅,陈维华,聂洪山.球面菱形网格递归剖分方法研究[J].)地理与地理信息科学, 2010,26(6):34-37. |
| [8] | ZHAO Xuesheng, BAI Jianjun. Hierarchical Model of Global Discrete Grids Based on Diamonds[J].Journal of China University of Mining and Technology,2007,36(3):397-401.(赵学胜,白建军.基于菱形块的全球离散格网层次建模[J].)中国矿业大学学报, 2007,36(3):397-401. |
| [9] | BEN Jin, TONG Xiaochong, YUAN Chaopeng.Indexing Schema of the Aperture 4 Hexagonal Discrete Global Grid System[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(6): 785-789.(贲进,童晓冲,元朝鹏.孔径为4的全球六边形格网系统索引方法[J].)测绘学报, 2011, 40(6): 785-789. |
| [10] | BAI Jianjun.Location Coding and Indexing Aperture 4 Hexagonal Discrete Global Grid Based on Octahedron [J].Journal of Remote Sensing,2011,15(6):1131-1146.(白建军.基于正八面体的四孔六边形球面格网编码及索引[J].)遥感学报, 2011,15(6):1131-1146. |
| [11] | TODD R, PETERSEN M, ROBERT L. A Multi-resolution Approach to Global Ocean Modeling[J]. Ocean Modelling, 2013, 69:211-232. |
| [12] | WHITE D.Comparing Area and Shape Distortion on Polyhedral-based Recursive Partitions of the Sphere[J]. International Journal of Geographical Information Science, 1998,12(8): 805-807. |
| [13] | SATOH M,MATSUNO T,TOMITA H,et al. Nonhydrostatic Icosahedral Atmospheric Model (NICAM)for Global Cloud Resolving Simulations[J]. Journal of Computational Physics, 2008, 227:3486-3514. |
| [14] | YUAN Wen, MA Ainai, GUAN Xiaojing. A New Projection for Spherical Triangle:Equal Angle Ratio Projection (EARP)[J]. Acta Geodaetica et Cartographica Sinica,2005,34(1):78-84.(袁文,马蔼乃,管晓静.一种新的球面三角投影:等角比投影(EARP)[J]. )测绘学报, 2005,34(1):78-84. |
| [15] | BEN Jin,TONG Xiaochong,ZHANG Yongsheng,et al. Research on Generating Algorithm and Software Model of Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2006, 36(2): 187-191. (贲进,童晓冲,张永生,等.球面等积网格系统生成算法与软件模型研究[J].)测绘学报, 2007,36(2): 187-191. |
| [16] | TONG Xiaochong, BEN Jin, WANG Yin. A New Effective Hexagonal Discrete Global Grid System: Hexagonal Quad Balanced Structure[C]//Proceedings of 2010 18th International Conference on Geoinformatics. Beijin:[s.n.], 2010: 1-6. |
| [17] | FEKETE G, TREINISH L.Sphere Quadtrees: A New Data Structure to Support the Visualization of Spherically Distributed Data[C]//Proceedings of SPIE on Extracting Meaning from Complex Data: Processing, Display, Interaction.[S.l.]:SPIE, 1990: 242-253. |
| [18] | SAHR K, WHITE D, KIMERLING J.Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003,30(2): 121-134. |
| [19] | WHITE D. Global Grids from Recursive Diamond Subdivisions of the Surface of an Octahedron or Icosahedron[J]. Environmental Monitoring and Assessment, 2000, 64(1): 93-103. |
| [20] | MING Tao, YUAN Wen, PENG Guagnxiong, et al. The Study on Error Analysis of Discretization Area in Discrete Global Grid System[J].Procedia Environmental Science,2011,10(B):1122-1128. |