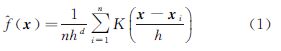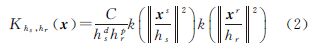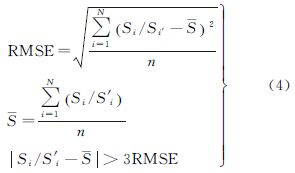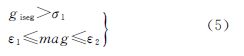2. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079,China
1 引 言
搭载全景相机传感器的车载移动测量系统,可完成沿道路360°场景的全景影像数据采集。由于立体模型较好地保持了平面影像特征,且可方便地引入经典的图像处理方法,因此采用立体模型构建全景影像,较容易进行影像匹配、提取与识别等应用[1]。
立体全景序列影像的匹配,目前主要采用SIFT多尺度特征匹配的方法[2],利用5点求解算法[3]并结合Ransac方法[4, 5],估计立体全景影像的极线几何模型,通过极线几何模型约束来控制粗差[1]。这种匹配策略在近景和航空航天影像中已广泛应用[6, 7, 8, 9, 10, 11]。区别于针孔影像,全景带来了全视角的影像信息,但增加了场景的复杂性,SIFT特征匹配后仍存在大量的重复纹理、运动物体和尺度变化等粗差,造成低内点率下Ransac极线几何模型估计不准确,这也是目前全景影像匹配的主要问题所在[12, 13, 14]。如果考虑全景序列影像间的运动关系来约束匹配,可以借鉴视频跟踪领域的光流特征匹配法,如基于光流特征的金字塔匹配方法[15]。但实际应用中发现,在车载全景影像的重复纹理区域、运动物体边界周围、深度不连续处,光流会发生剧烈的变化,不满足亮度恒定性假设,匹配结果往往仍存在大量的粗差。
综上,采用SIFT和光流匹配方法,已经不能完全解决车载全景影像的匹配问题。如何控制匹配过程中的重复纹理、运动物体、尺度变化等粗差是匹配的关键。
2 光流特征聚类的影像匹配方法2.1 光流特征聚类算法
车载全景序列影像采样间隔短,一般可认为满足视频序列影像特征,可以采用光流法实现影像间的特征匹配[15]。但该方法受重复纹理特征和搜索窗口的影响,在匹配亮度差最优求解中快速收敛于最邻近的相似纹理特征,产生重复纹理的匹配粗差,而全景影像中的场景运动关系复杂,尤其受车辆等运动物体影响,光流呈现整体的不规律性,因此仅采用亮度守恒度量显然无法提高匹配的可靠性。首先采用“Classic+NL-Fast”全局光流匹配算法[16]来分析车载立方体全景序列影像间的光流特征,分别得到光流场彩色编码图 1(a)和光流场矢量分布图 1(b)(数据见图 2(a))。由图 1可知,影像间不同物体满足不同的运动关系。对于建筑物、道路、运动物体等呈现出不同的光流运动矢量,并且随深度方向的变化而变化。主要特征如下:①建筑物区域反映出较强的光流场,并与深度方向成反比,而光流方向满足局部的一致性;②受道路相似性纹理影响,光流表现为静止运动,因此强度很弱,且满足光流方向的一致性;③测量车体本身为相对静止运动,光流强度很弱,且满足光流方向的一致性;④场景中的运动物体,光流场表现复杂,随运动物体与测量车产生的相对运动大小而变化,并与深度方向有关,但运动物体破坏了光流连续性,表现为局部光流异常变化的特征。

|
| 图 1 全景序列影像的全局光流场分析 Fig. 1 Global optical flow field analysis for vehicle-borne panoramic images |

|
| 图 2 相同内点率匹配对比试验(左为匹配点、线,右为匹配点线局部放大图) Fig. 2 Match results on same inlier ratio (left: match point/line,right: partial enlarged view) |
综上,全景影像的光流强度和方向满足局部一致性,且与空间分布相关,因此可以充分利用局部光流的统一性,来区别不同场景中的重复纹理和运动物体目标。这种局部光流的统一性,可以表达为特征匹配结果在影像空间中的显著光流特征的聚类。采用非参数化的均值漂移特征聚类思想[17, 18, 19],以SIFT多尺度特征匹配点的位置量和光流矢量,构建影像特征空间的空域和值域,利用特征空间中对应的显著图像光流特征为聚类条件,实现全景序列影像的匹配,算法描述如下。
2.1.1 光流聚类定义在d维空间Rd中,给定n个数据点xi,则点x处的多变量核密度估计器^f(x)的计算由式(1)给出,其中K(x)是核函数,h是核的大小[17]
由均值漂移算法可知,影像的特征空间可以表达为空-值联合域的形式,由此产生的联合域核函数Khs,hr(x)由两个径向对称核组成[18],见式(2)
式中,hs、hr分别代表空域和值域的核大小(带宽阈值);p、d表示空间维度;xs、xr是特征向量的空域和值域部分;kx是在两域中共同的核轮廓函数;c是规范化常数。
采用SIFT多尺度特征匹配点的位置坐标和光流矢量,构建影像特征空间的空域和值域。已知SIFT匹配点对的位置坐标为(u,v)、(u′,v′),表达为四维特征向量[w1uw2vw3δuw4δv],定义如下:
(1) 空域xs,由SIFT匹配点的位置坐标定义为(u,v)。
(2) 值域xr,由SIFT匹配点的光流矢量定义为(δu,δv),见式(3)
(3) w1、w2、w3、w4定义空域与值域的权值大小。 2.1.2四维特征向量权的确定
以显著光流特征为聚类条件,光流矢量的权值在聚类中的贡献比重更大,如定义初始权(w1,w2,w3,w4)为(1,1,10,10)。另外具有相同SIFT尺度特征的匹配点表现为物方上的尺度相似性,匹配点满足尺度上的相似性条件,可有效避免尺度空间内不稳定的匹配点,因此可以通过尺度特征进一步确权。已知SIFT初始匹配点个数为n,匹配点的特征尺度为Si,Si′,均值漂移搜索带宽半径内匹配点的平均尺度比例值为,定义尺度比例值大于3倍中误差RMSE为尺度不一致的匹配点,设置权值为极大值,尺度的定义如下
2.1.3 带宽阈值的估计光流聚类的带宽hs,hr估计可以用特征光流的幅度大小来定义,受相机与物体间的运动影响,也受场景中物体的远近影响。对于场景中的“重要地物”,如建筑物的特征光流,一般满足一定的幅度变化,而这个幅度范围与相机间运动距离、影像幅宽和建筑物远近相关,可以通过统计光流幅度直方图近似获得,本文试验数据幅度大小主要在0~300个像素范围内。
2.1.4光流聚类匹配将上面定义的加权四维特征向量代入式(1)、式(2)中,采用均值漂移解法实现匹配特征点的聚类[18]。聚类结果表现为局部光流一致性的点被聚类到一起,通常为大样本点,而光流异常点(通常表现为重复纹理和运动目标产生的光流异常点)也被聚类到一起,往往为小样本点,即某个聚类包含了极少的匹配点(见图 2(d))。另外,场景中的相对静止匹配点或光流变化的极值点,表现为光流幅度变化满足一定的阈值范围。因此定义光流聚类匹配的条件为满足聚类点数giseg大于一个阈值σ1,且光流幅度mag满足一个阈值范围[ε1,ε2],见式(5)
2.2 算法流程匹配方法基于零假设H0,序列影像对I和I′有随机独立匹配点mi∈I,m′i∈I′,则具体算法流程如下:
(1) 采用SIFT特征匹配方法,获取全景影像尺度空间上的初始匹配点。
(2) 由尺度空间的初始匹配点,定义四维特征向量(w1u,w2v,w3δu,w4δv),设置初始权(w1,w2,w3,w4)为(1,1,10,10),由式(4)定义尺度不一致的向量权值为极大值。
(3) 以步骤(2)中定义的加权四维特征向量为影像特征空间的空域和值域,带宽阈值由光流幅度的大小定义,代入式(1)—式(2)求解均值漂移向量,得到光流特征的初始聚类。利用式(5)对初始聚类结果进行筛选,完成光流聚类匹配。
(4) 最后对光流聚类匹配的结果,利用全景极线几何约束匹配[1, 2, 3]。
3 试验及其结果分析试验数据为拓普康IP-S2车载移动测量系统获取的全景序列影像。首先将球面全景映射为立体模型全景影像[20],由于上下视图为天空和地面,信息量很小,所以仅保留左、前、右、后4个视图,影像的宽高大小为5400像素×1350像素。采用正确匹配点数、正确匹配率和计算时间3个指标评价结果,选择Ransac方法[1]、金字塔Lucas-Kanade光流法[15](以下简称OFPLK)和本文方法做比较,分别进行相同内点率、不同内点率、不同数据的对比试验。无特殊说明,试验参数统一设置为(单位为像素):极线几何约束的投影差阈值为1[5],均值漂移算法中的带宽阈值hs=hr=250,光流聚类阈值σ1=12,光流幅度阈值ε1=10、ε2=500。OFPLK方法中的搜索窗口为30,跟踪误差阈值为10。
3.1 相同内点率的对比试验试验采用测试数据1,见图 2(a)。首先利用SIFT进行初始特征匹配,SIFT最近邻比例因子为0.7。试验结果如表 1和图 2所示。
| 影像 | 方法 | SIFT初始匹配点数 | 匹配点数 | 匹配粗差点数 | 正确匹配点数 | 正确匹配率 | 计算时间/s | 聚类(前/后) |
| Ransac | 3428 | 1311 | 286 | 1025 | 0.782 | 6.442 | — | |
| 1 | OFPLK | 3428 | 1215 | 195 | 1020 | 0.840 | 2.293 | — |
| 本文方法 | 3428 | 1734 | 22 | 1712 | 0.987 | 18.383 | 104/12 |
由表 1可知,本文方法能较好地控制粗差,在正确匹配点数和正确匹配率方面均高于Ransac和OFPLK方法,达到了0.987正确匹配率,获取104个初始聚类,经过光流聚类匹配后剩余12个聚类,见图 2(d)、图 2(e)。而在计算时间上Ransac和OFPLK方法更优,本文方法在聚类匹配过程中耗费了更多的时间。
图 2(a)显示经过SIFT初始匹配后,仍含有大量的粗差。基本表现为由建筑物和道路纹理重复性造成的粗差、车体本身相对静止粗差以及运动物体粗差。另外,深度方向的远处场景中存在大量的匹配点,但由于其交会角很小而且分辨率低,所以匹配精度也很低。图 2(b)为Ransac方法极线几何约束后的匹配结果。从图中标识的区域可以看出仍存在明显的粗差:区域“A”为运动物体粗差,区域“B”表现为受整体模型估计不准确误删除的大量正确匹配点,区域“C”为无法剔除的低精度远处匹配点,区域“E”为相似纹理粗差。区域“C”局部放大图中可以清晰地看出仍存在远端低精度匹配点和道路相似性纹理的匹配粗差等。图 2(c)为OFPLK方法的匹配结果,对比Ransac方法可以看出,区域“A”仍存在运动物体粗差,区域“B”获取了相对多的正确匹配点,区域“C”正确匹配点减少,区域“D”为采集车自身由于相对静止产生的粗差。图 2(d)为本文方法光流聚类的结果,总计104个类别用不同的颜色显示。从匹配线的聚类结果可以看出,相同的颜色聚类代表光流矢量的一致性,而这种聚类呈现出局部的平面特征,并且正确的匹配点表现为大的类别。对于粗差点往往被聚类到小类别中,光流矢量表现为与周边异常现象(见右侧局部放大图)。图 2(e)为本文方法匹配后的聚类结果,剩余12个类别用不同的颜色显示。试验结果可以证明,正确的光流匹配结果往往集中在大的类别中,因此本文光流聚类的方法,对于小类别表现为粗差的概率很高。与图 2(b)中对应的标识区域进行对比分析可得,本文方法可以较好地保留建筑物正确匹配点,对于运动物体、道路相似纹理粗差以及远距离低精度匹配点具有较好的约束效果。表 1的统计结果显示本文方法约束后粗差点数为22,仍存在部分粗差点无法完全清除。观察发现这些粗差主要表现为部分运动物体粗差和天空粗差点,尤其当场景中运动物体大量存在的情况下,无法通过光流聚类来区别粗差点,而天空点主要表现为距离建筑物的边缘3个像素左右的点,实际观察纹理和位置为正确匹配,但由于没有附着在地物上,这种匹配点实际是无效的。
3.2 不同内点率的对比试验采用测试数据1,利用SIFT最近邻比例因子“SIFT_Ratio”来生成不同内点率的初始匹配数据,SIFT_Ratio值越大代表粗差率越高,即内点率越低。
图 3(a)与图 3(b)显示不同内点率下的试验结果。可以看出随着内点率的降低,尤其在低内点率SIFT_Ratio取0.95和0.98情况下Ransac方法正确匹配点数很低,而且匹配率下降到67.6%和61.2%,验证了Ransac方法在内点率极低的情况下模型估计十分不稳定。而OFPLK方法正确匹配点数整体优于Ransac方法,正确匹配率与Ransac方法近似,尤其在SIFT_Ratio为0.9~0.98之间时获得了优于本文方法的正确匹配点数,但其正确匹配率却远远低于本文方法。观察图 3(a)、图 3(b),可以看出本文方法在不同内点率试验中表现十分稳定,正确匹配率均在92%以上,高于Ransac和OFPLK方法。图 3(c)显示随着内点率的降低,3种方法计算效率逐渐下降,但Ransac和OFPLK方法计算效率更高。本文方法主要受聚类算法的影响,内点率越低聚类数越大,导致计算效率下降。
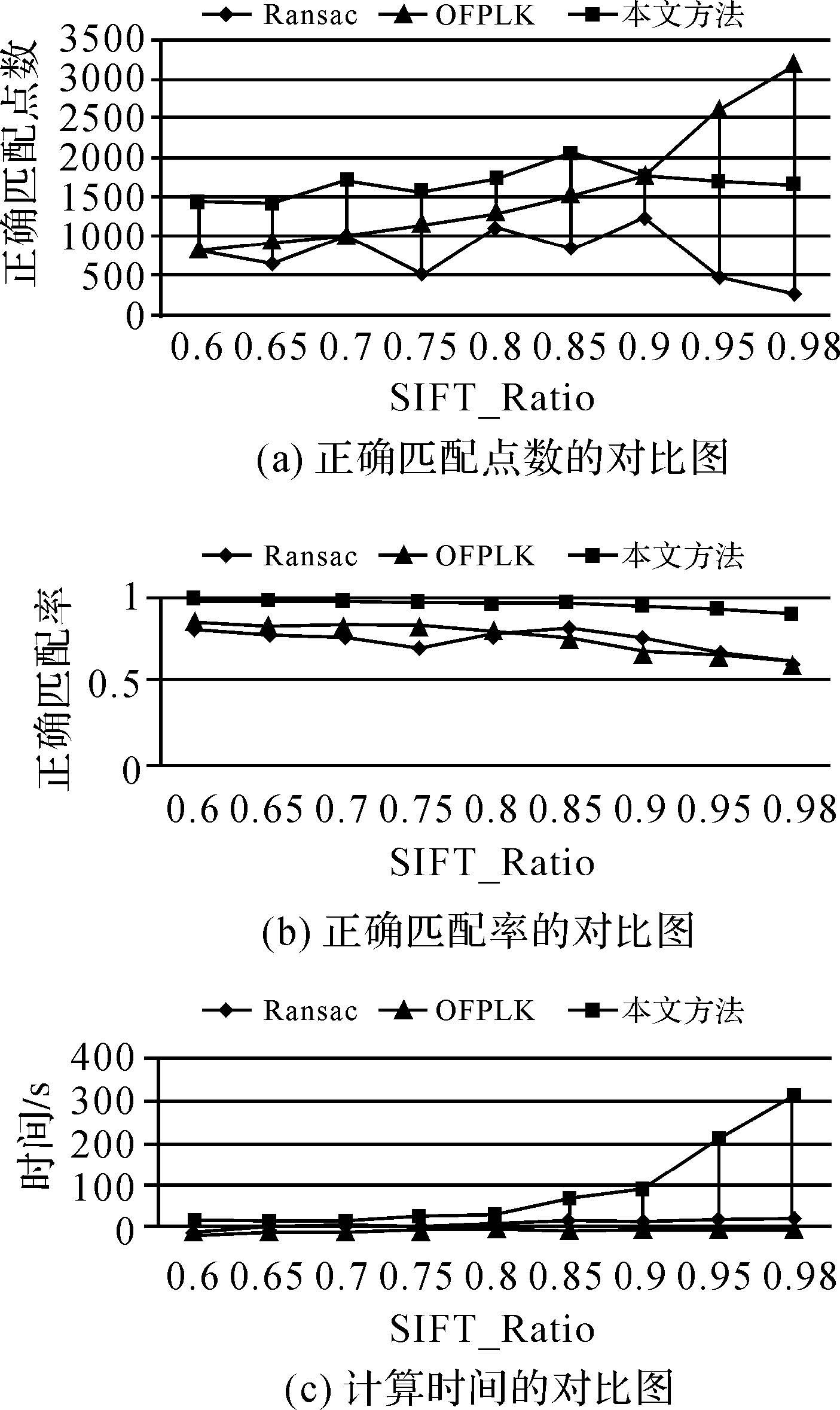
|
| 图 3 不同内点率的对比试验折线图 Fig. 3 Line chart experiment results on different inlier ratio |
采用16组不同场景的测试影像评价本文算法的稳定性,SIFT最近邻比例因子SIFT_Ratio=0.7,其中5组数据统计值见表 2,图 4为16组数据的试验对比柱状图。
| 测试影像对 | 方法 | 初始匹配点数 | 正确匹配点数 | 正确匹配率 | 计算时间 | 聚类 |
2  | Ransac | 3393 | 2149 | 0.837 | 4.955 | — |
| OFPLK | 3393 | 497 | 0.606098 | 2.31 | — | |
| 本文方法 | 3393 | 1926 | 0.992 | 17.813 | 176 | |
4  | Ransac | 1953 | 565 | 0.808 | 3.14 | — |
| OFPLK | 1953 | 801 | 0.765043 | 1.951 | — | |
| 本文方法 | 1953 | 689 | 0.812 | 11.176 | 113 | |
8  | Ransac | 1543 | 242 | 0.661 | 2.591 | — |
| OFPLK | 1543 | 744 | 0.712644 | 2.069 | — | |
| 本文方法 | 1543 | 472 | 0.863 | 10.353 | 94 | |
10  | Ransac | 802 | 79 | 0.564 | 1.384 | — |
| OFPLK | 802 | 105 | 0.242494 | 1.622 | — | |
| 本文方法 | 802 | 129 | 0.737 | 6.026 | 82 | |
16  | Ransac | 2108 | 675 | 0.802 | 3.358 | — |
| OFPLK | 2108 | 911 | 0.826679 | 1.967 | — | |
| 本文方法 | 2108 | 944 | 0.993 | 13.919 | 113 |
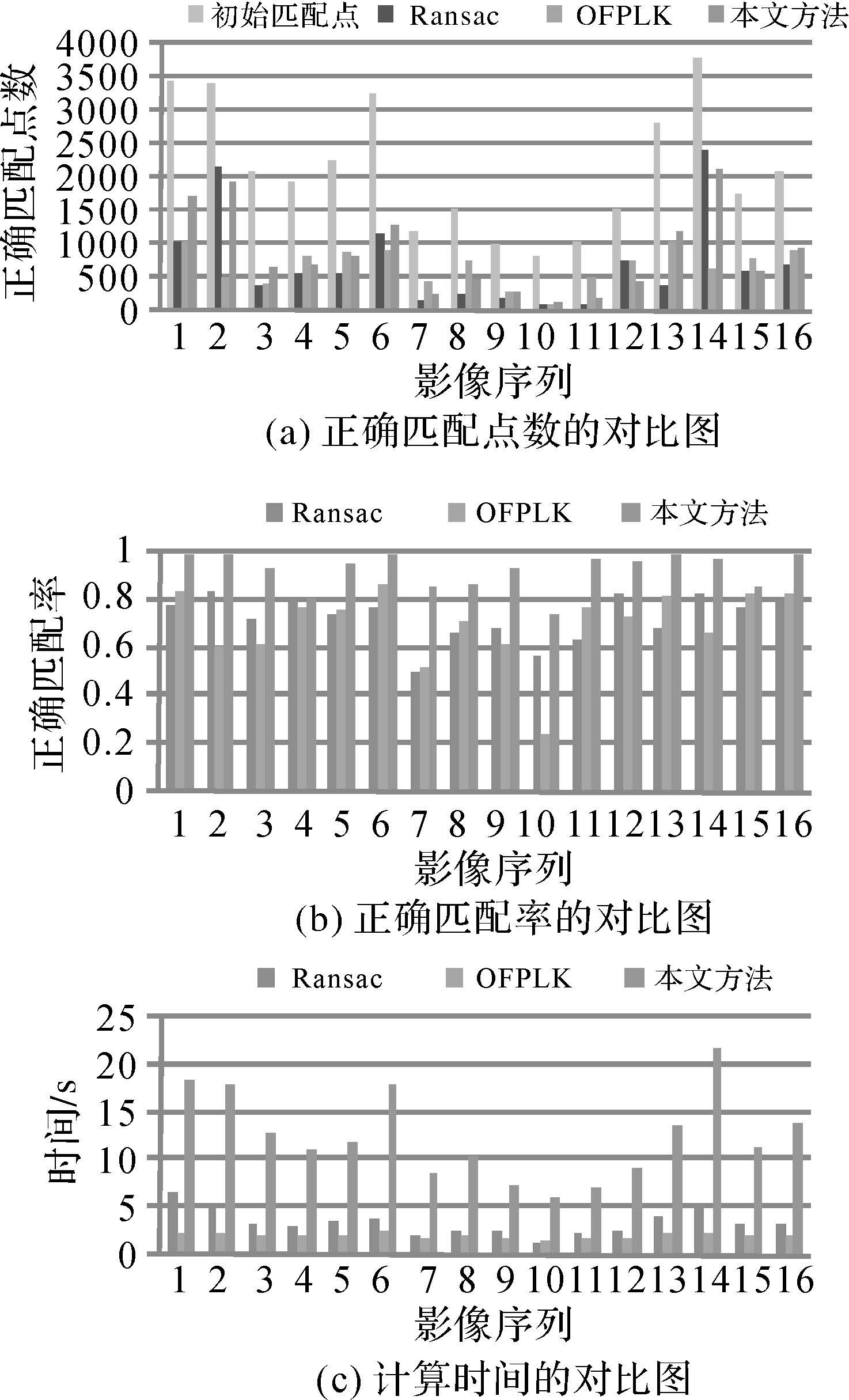
|
| 图 4 16组数据的对比试验柱状图 Fig. 4 Histogram experiment results on sixteen sets of data |
由图 4(a)可知,本文方法的正确匹配点数整体上优于Ransac方法,部分数据略低于OFPLK方法。但在正确匹配率方面,均优于其他两种方法,并且大部分情况下在90%以上。计算时间方面Ransac和OFPLK方法有明显的优势。
表 2中的第10组数据选择为空旷场景,由于特征地物稀少,场景中基本都是相似性纹理。SIFT初始匹配含有极大的粗差点,Ransac正确匹配79个点,OFPLK正确匹配105个点,本文方法正确匹配129个点。在正确匹配率方面,Ransac方法为56.4%,OFPLK方法为24.2%,本文方法为73.7%,虽然3种方法的正确匹配率都较低,但本文方法还是有明显的优势。观察匹配数据可以发现,在特征不明显的区域,且数据质量不清晰情况下,算法表现出一定的稳定性,但仍然含有一定的粗差,此类粗差为场景中出现的大量车流导致,其运动规律表现为统一的运动速度和方向,满足光流的显著性聚类条件,因此本文方法也很难检测出来。
4 结 论本文研究了一种光流特征聚类的车载全景序列影像匹配方法。通过不同参数的对比试验,结果表明对于街景复杂、内点率较低的情况下,该算法表现出极好的稳定性,可以在一定程度上控制重复纹理粗差、尺度变化粗差和区分部分运动粗差,有效提高了正确匹配点数和匹配率,但由于引入了均值漂移的光流聚类方法,因此在计算效率上要低于Ransac和OFPLK方法。另外受相关阈值影响,如何面对不同场景,研究自适应的阈值进一步提高聚类的精度,将有助于粗差的检测。同时发现该方法仍然存在一定的粗差无法检测问题,尤其在低内点率的空旷场景或车流密集场景,这些粗差均满足光流和极线几何的约束,研究增加其他几何约束条件来进一步控制此类粗差是下一步研究的方向。
| [1] | KANGNI F, LAGANIERE R. Epipolar Geometry for the Rectification of Cubic Panoramas[C]//Proceedings of the 3rd Canadian Conference on Computer and Robot Vision. Halifax: IEEE, 2006, 70-70. |
| [2] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [3] | NISTR D. An Efficient Solution to the Five-point Relative Pose Problem [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756-770. |
| [4] | FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].Communications of the ACM, 1981, 24(6): 381-395. |
| [5] | HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. 2nd ed. Cambridge: Cambridge University Press, 2003. |
| [6] | JIANG Wanshou, ZHENG Shunyi, ZHANG Zuxun, et al. Feature-based Image Matching for Aerial Images[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 510-513. (江万寿, 郑顺义, 张祖勋, 等. 航空影像特征匹配研究[J]. )武汉大学学报: 信息科学版, 2003, 28(5): 510-513. |
| [7] | LI Xiaoming, ZHENG Lian, HU Zhanyi. SIFT Based Automatic Registration of Remotely-sensed Imagery[J]. Journal of Remote Sensing, 2006, 10(6): 885-892. (李晓明, 郑链, 胡占义. 基于SIFT特征的遥感影像自动配准[J]. )遥感学报, 2006, 10(6): 885-892. |
| [8] | LIANG Dong, TONG Qiang, QU Lei, et al. Algorithm for Images Matching Based on Epipolar and Homography Constraints[J]. Journal of System Simulation, 2006, 18(1): 44-46. (梁栋, 童强, 屈磊, 等. 一种基于极几何和单应约束的图像匹配算法[J]. )系统仿真学报, 2006, 18(1): 44-46. |
| [9] | LV Jinjian, WEN Gongjian, LI Deren, et al. A New Method Based on Spatial Relations for Feature Matching [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3), 367-373. (吕金建, 文贡坚, 李德仁, 等. 一种新的基于空间关系的特征匹配方法[J]. )测绘学报, 2008, 37(3), 367-373. |
| [10] | ZHANG Ka, SHENG Yehua, YE Chun. Digital Close-range Stereo Image Matching Based on Digital Parallax Model and Improved SIFT Feature[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 624-630. (张卡, 盛业华, 叶春. 基于数字视差模型和改进SIFT特征的数字近景立体影像匹配[J]. )测绘学报, 2010, 39(6): 624-630. |
| [11] | ZHAO Xian, CHEN Zhixue, LV Jingguo, et al. The Scale and Rotating Invariant Auto Stereo Matching[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 81-86. (赵西安, 陈志学, 吕京国,等. 具有尺度与旋转不变性的立体影像自动匹配研究[J]. )测绘学报, 2012, 41(1): 81-86. |
| [12] | SATO T, PAJDLA T, YOKOYA N. Epipolar Geometry Estimation for Wide-baseline Omnidirectional Street View Images[C]//Proceedings of 2011 IEEE International Conference on Computer Vision Workshops. Barcelona: IEEE, 2011: 56-63. |
| [13] | NI K, JIN H L, DELLAERT F. GroupSAC: Efficient Consensus in the Presence of Groupings [C]//Proceedings of IEEE 12th International Conference on Computer Vision. Kyoto: IEEE, 2009: 2193-2200. |
| [14] | MICUSIK B, KOSECKA J. Piecewise Planar City 3D Modeling from Street View Panoramic Sequences[C]//Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 2906-2912. |
| [15] | BOUGUET J Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker: Description of the Algorithm[R].California:Intel Corporation Microprocessor Research Labs,2002. |
| [16] | SUN D, ROTH S, BLACK M J, et al. Secrets of Optical Flow Estimation and Their Principles[C]//Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2432-2439. |
| [17] | FUKUNAGA K, HOSTETLER L. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1): 32-40. |
| [18] | COMANICIU D, MEER P. Mean Shift: A Robust Approach toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. |
| [19] | CHRISTOUDIAS C M, GEORGESCU B, MEER P. Synergism in Low Level Vision[C]//Proceedings of 16th International Conference on Pattern Recognition. Quebec: [s.n.], 2002: 150-155. |
| [20] | TANG Jin. Omnidirectional Image Based on IBR[D]. Changsha: Central South University, 2002. (唐琎. 基于IBR的全方位全景图像[D]. )长沙: 中南大学, 2002. |