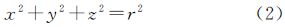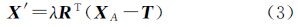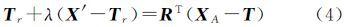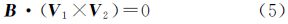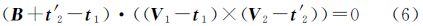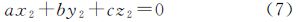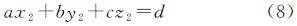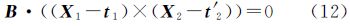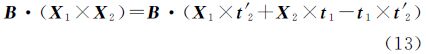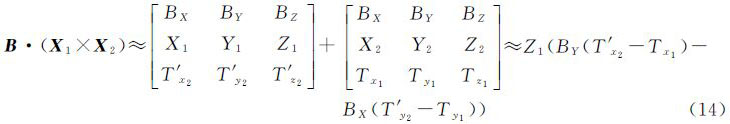2. 中国农业科学院 农业资源与农业区划研究所 农业信息技术重点实验室,北京 100081;
3. 东京大学 空间信息科学研究中心,东京
2. Key Laboratory of Agri-informatics Institute of Agricultural Resources and Regional Planning,Chinese Academy of Agricultural Sciences,Beijing 100081,China;
3. CSIS,the University of Tokyo,Tokyo,Japan
1 引 言
借助360°无缝成像的优势,全景相机正逐渐受到计算机视觉、机器人、测绘等研究领域的青睐和广泛应用[1, 2, 3]。主流数码全景相机的成像方式分为3大类:折射式(dioptric)多镜头组合、折反射(catadioptric)系统和旋转式扫描系统。多镜头组合型全景相机由一系列独立、固定的镜头组成,多个镜头独立成像,再拼接为全景影像,该类型相机如LADYBUG[4, 5]。折反射系统由鱼眼镜头和抛物镜面组成。抛物镜反射实体的光,并通过透镜折射形成球面影像[6, 7]。旋转式线阵扫描成像借助高速旋转的机械转轴和单镜头或单根CCD,直接形成无缝全景影像而无需拼接[8, 9]。3种全景相机都有自身的缺点。多镜头组合相机由于存在拼接步骤,物体景深的不可知性导致拼接误差必然存在,即无法实现真无缝拼接;折反射系统由于抛物镜面只能反射部分现实的光线,难以实现全视角;扫描式相机受载于高速运动平台时会产生较大的几何形变,一般只用于静态或低速摄影;而多镜头组合相机和折反射相机可用于车载或机载。本文着重讨论多镜头组合式全景相机。
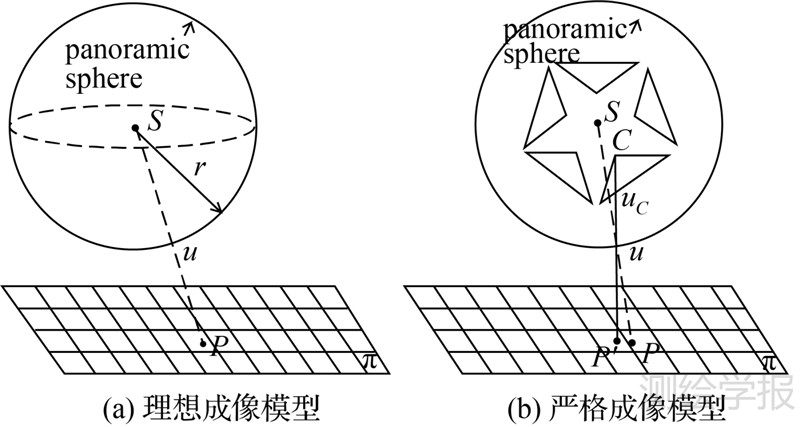
与传统平面相机类似,多镜头组合型全景相机的基本成像几何也基于针孔成像模型,表达像、物及投影中心三点之间的共线关系。在很多有关全景相机的文献中,成像几何往往被简化成图 1(a)所示的理想的模型:一个投影中心和一个理想投影球面。文献[10]使用针孔球面成像模型进行实时SLAM(simultaneous localization and mapping);文献[11]研究了全景影像的全局几何特征描述;文献[12]基于球面成像模型研究球面影像块的旋转缩放不变特性;文献[13]利用球面成像基础矩阵作为立体像对间的几何约束;文献[14]研究了基于全景单相机的视觉SLAM;文献[15]研究了车载全景相机的影像匹配和光束法平差。这些文献都采用了图 1(a)所描述的理想全景球面成像模型。事实上,多镜头组合型全景照相机是由数个独立透镜组成,可能具有不同的投影中心和焦距(图 1(b))。如果使用理想的全景成像模型来描述其成像特性,必然会引入一定的系统误差。
|
| 图 1 全景相机成像模型 Fig. 1 The panoramic ideal sensor model and the rigorous sensor model |
针对全景理想模型的缺陷,文献[16]根据多镜头球面成像特性提出了一种严格成像模型;然而,并未对理想模型的系统误差及该误差对精确定位的影响进行详细分析,且未对两种模型进行实际数据的比较。本文的主要工作将解析地推导理想模型所引起的物方、像方定位误差和立体像对核线误差,通过室内外实际数据的比较试验,包括空间后方交会、核线约束、光束法平差,验证理想模型系统误差的变化规律,总结理想模型和严格模型的适用范围。
2 全景相机的成像模型 2.1 全景相机的理想成像模型图 1(a)示意了全景相机的理想成像模型,表达了球心S、球面像点u及对应物方点P三点共线的几何关系。而事实上,多镜头组合式全景相机由多个独立鱼眼相机组成,每个相机具有各自的投影中心C,其与球心S难以实现完全重合,如图 1(b)所示。为将独立相机影像转换为全景影像,首先需要将独立相机的影像坐标转换为统一的全景球面坐标。式(1)描述了如何根据单相机像点uc(其三维坐标用X表示)来计算全景球面像点u(其三维坐标用X′表示)。式中,Kr表示各个鱼眼相机的内部标定参数矩阵,主要包含镜头畸变差、CCD畸变差、焦距、主点位置等[17];Rr和Tr分别表示独立相机投影中心在全景坐标系统中的外方位元素角元素矩阵和偏移矢量;Kr、Rr、Tr通过严格的全景相机标定之后即为固定值;m为待求之比例系数。式(2)描述任一球面像点u的三维坐标X′=[x y z]T必须位于半径为r的球面上,如何最优地选择该半径值可参考文献[18, 19]。联立式(1)、式(2),可解得m和X′
获得球面坐标X′后,根据图 1(a)的理想模型可列出3点共线的几何关系。在式(3)中,R、T来分别表示角元素矩阵和线元素矢量,XA表达对应物方点P的三维坐标,λ为比例系数
式(3)所表达的全景相机理想成像模型为大部分文献广泛采用,然而,从图 1(b)可看出,用于表述理想共线条件方程的光束投影SuP与独立相机实际光束投影CuP′是有偏差的。原因即S和C无法严格重合。
2.2 全景相机的严格成像模型文献[16]提出了一种针对多镜头组合全景相机的严格成像模型,以描述实际光束CuP′,如下式
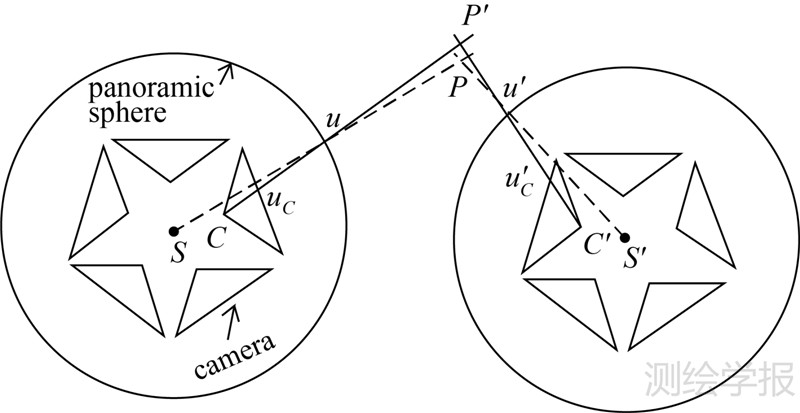
式中,Tr表示单个相机投影中心在全景坐标系下的偏移矢量,即图 1(b)中C点相对于S的矢量。相较于该严格模型,式(3)表达的理想成像模型无论被用于计算像方坐标(后方交会)还是计算物方坐标(前方交会),都会由于忽略了真实存在的Tr而引入系统误差。不过,Tr可能是一个微小量,如本文使用的商业全景相机Ladybug3的Tr,在平面方向约为4cm,在高程方向优于0.02cm(仅考虑5个水平摄影镜头)。而对于一些自制全景相机,Tr在平面方向可达到分米级甚至更大,此时理想模型将导致较大的系统误差。 2.3 全景相机的共面条件方程传统框幅式相机立体像对之间的共面条件描述了两个投影中心和同名像点之间的共面关系[20, 21]。同样共面条件也存在于全景立体像对中。图 2中虚线描述了基于理想成像模型的共面关系,即理想球面中心点S和S′、全景像点u和u′及物点P满足共面条件。将基线SS′表示为B=[BX BY BZ]T、光线Su表示为V1=[X1 Y1 Z1]T=[x1 y1 z1]T、光线S′u′表示为V2=[X2 Y2 Z2]T=R[x2 y2 z2]T,R为摄站间的相对旋转矩阵,则理想的共面条件方程
|
| 图 2 全景立体共面条件示意图(虚线:理想模型;实线:严格模型) Fig. 2 Co-planity of the two models (dotline: the ideal model; solid line: the rigorous model) |
相应的,设t1、t2分别是立体像对全景球心S、S′与独立相机C、C′的偏移量,t′2=Rt2为旋转至左片坐标系下的独立镜头偏移量,则严格的共面条件方程
在相对定向元素已知时,可根据共面方程导出核线方程。式(7)是理想模型的核线方程,系数a、b、c完全由相对定向元素确定。传统平面影像的核线是一条直线,而三个维度确定的理想全景影像核线是一个过球心的大圆
式(8)是严格模型的核线方程,同样的,系数a、b、c、d由相对定向元素确定,而常数项不为0说明核线不再是经过球心,而是有一个微小的偏移量 3 理想成像模型的系统误差分析虽然理想全景模型被广泛采用,但是严格全景模型理论上显然更加严密,以下将分别从单光线定位与后方交会,立体像对核线约束等方面分析理想模型的系统误差。
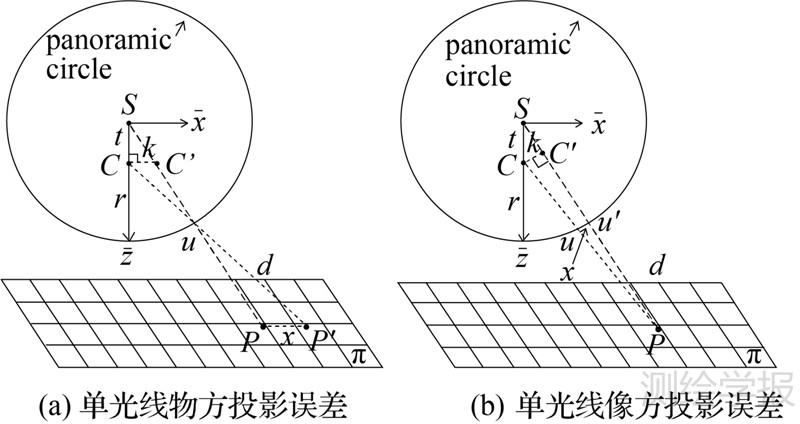
3.1 单光线物方投影误差假设方位元素和物方投影面高程已知,可获得投影点的物方平面坐标。不失一般性,仅考虑x方向的系统偏差。如图 3(a)所示,真实物体P′过实际投影中心C,成像于u,物像距离为d,全景理想模型认为投影中心为S,使得P′被移动至P。设z方向为独立相机主光轴方向,侧视角为k,独立相机到球心距离为t,且由于t非常小,Cu≈Su=r,则根据相似三角可得
式中,t、r可视作常量,则投影误差是物像间距d、侧视角k的函数。一般而言,物像距离根据镜头的参数而定,对于本文采用的Ladybug3系统,最佳全景球面半径r为20m,最远成像距离不宜超过40m,则物像间距最大为20m;另一方面,近距离物体会引起较大的拼接误差,最近一般不超过4m,则物像距离d∈(-20m,16m)(指向球心为正)。最大侧视角k由独立相机个数计算,5个侧视相机平均分摊72°视角,可得k∈(0°,36°)。此时可得两极最大误差-0.025m和0.02m,分别在k=36°,d=-20m和k=36°,d=16m时取得。然而,在影像配准、匹配、平差等处理流程中,只有少量的影像边缘点会被采用,绝大部分点的投影误差不会超过0.01m,根据式(10)换算为像素,即0.5像素,可认为是一个小量(Ladybug3焦距f为3.3mm,像素大小p0为4.4um)
|
| 图 3 理想全景模型单光线投影误差示意图 Fig. 3 The single ray localization errors of the ideal panoramic models |
类似可分析单光线像方投影误差。如图 3(b),真实像点u被移动至u′。过C作SP垂线并交之于C′,则根据三角相似可得
与物方投影误差相仿,其误差也与侧视角k,物像间距d相关。最大误差近-0.1m,于k=36°,d=16m处取得。
3.3 核线误差相较于式(6),式(5)忽视了独立相机到全景球心的偏移量而导致理想模型的核线误差。推导简便起见,相较于B,t1、t2是可略的微小量,可将式(6)写为
合并、展开得到 式中,等式左边代表了理想核线模型,而等式右边不为0,恰反映了理想核线模型的系统误差。将微小项t1×t′2忽略,并只考虑水平摄影,即BZ=0、Z1=Z2,则继续简化可得 式中,理想核线误差与摄影基线B、旋转矩阵R和左片的Z1坐标相关。如果无旋转,则核线误差为0;相反的,核线误差随旋转角增大而增加。BX反映立体像对间的尺度,设置为1,BY一般小于BX。若只考虑车载全景相机水平旋转,R可仅由水平旋转角k表达。考虑通常的情况:设k∈(0°,30°),球半径20m,Z1∈(-16m,16m),再令BY=0.2m,代入式(14)可得最大误差为0.25m,在Z1=±16m,k=30°时产生。根据式(10)可知此误差相当于10像素。 4 试 验 4.1 试验设计为验证本文所推导的全景理想模型误差分布的正确性,采用两组典型实际数据进行试验。试验所用的全景相机统一采用LadyBug3系统,其独立鱼眼镜头成像大小为1616像素×1232像素,全景影像球面半径为20m。第1组试验数据在室外环境中采集,采用车载全景相机拍摄了3张影像,间隔1m,并布设8个控制点,控制点由Trimble 5800 GPS接收机搭配全站仪测量获取,3D定位精度约2cm,如图 4(a)所示。第2组试验数据取自室内走廊,5张影像由安置于手推车上的全景相机获取。图 4(b)是采用高精度Rigel VZ1000 LIDAR获取的全景伪影像,其定位精度约3mm。白色三角代表实际控制点,黑色圆圈代表检查点。这两组数据具有明显的差异。室内影像的物距约3~8m,旋转角相对较大,约15°;而室外数据的物距约10~25m,旋角近于0。从式(11)、式(14)可知,投影球面(像距)固定时,物距和旋转角正是理想模型系统误差的关键参数。

|
| 图 4 室内外全景数据及控制点 Fig. 4 The indoor and outdoor panoramic images and GCPs |
采用以上两组数据,共设计了3组对比试验。第1组比较两种模型的空间后方交会误差;第2组比较核线误差;第3组进行光束法平差以分析3D定位误差。
4.2 空间后方交会误差分析表 1显示了空间后方交会的结果。在室外试验中,两个模型的中误差(σ0),外方位元素(EO)精度几乎完全一致。从式(11)可知,像方的定位精度受视角大小和物像间距的综合影响;由于室外数据的物距在10~25m之间,即物像间距为-10~5m,使得部分控制点即使位于较大的视角上,也能保证很小的像方定位误差。
| 模型 | 控制点数 | σ0/m | 外方位元素精度 | |||
| 线元素/m | 角元素/rad | |||||
| 理想 | 室外 | 8 | 0.0201 | 0.003 | 2.5×10-5 | |
| 严格 | 0.0189 | 0.003 | 2.8×10-5 | |||
| 理想 | 室内 | 10(11) | 0.046(0.120) | 0.004 | 3.3×10-5 | |
| 严格 | 0.026(0.028) | 0.002 | 1.7×10-5 | |||
与此相反,室内试验显示了两种模型的明显区别。理想模型的σ0比严格模型精度低2cm,EO的精度也相对较低。由于物距是3~8m,与室外相比,大视角的控制点产生更大的定位误差。括号内是新增了一个位于5号鱼眼相机的控制点的结果,可见理想模型的中误差大大增加,原因是5号相机指向天空,与其他的4个水平指向相机不在同一平面。对严格模型而言,是否引入5号相机控制点,其精度几乎不变。
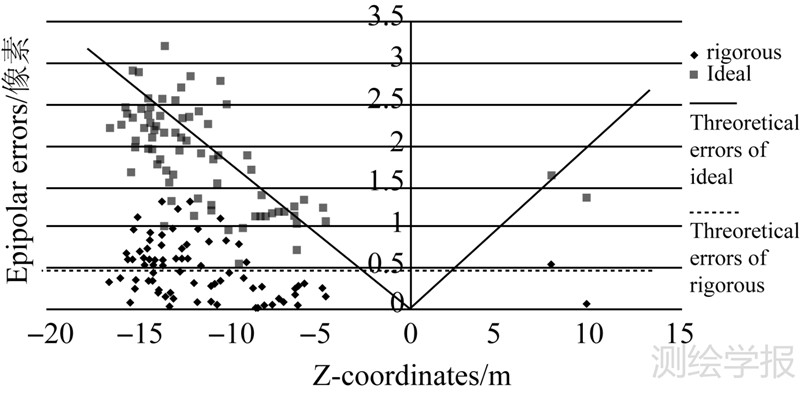
4.3 核线误差分析为验证核线误差,首先从一组立体像对中通过影像匹配精确提取了足够的同名像点,并根据两种模型分别计算了相对定向元素,其中,水平旋转角k为6.88°,其他两个角度为0。然后根据式(7)、式(8)计算右影像核线。取右片同名像点到核线的最小距离代表核线误差。图 5显示了79个同名点的核线误差,严格模型的核线误差(菱形)平均为0.48像素,与匹配精度相当;随着Z坐标的增加,核线误差有微小的增加趋势,可能由相机检校的微小误差引起。而对于理想模型,核线误差(方形)明显更大,平均约1.88像素,并且随着Z坐标的增加而增加。对称实线表示根据式(14)绘制的理想模型核线的理论误差分布,可见理论分布与实际误差的一致性。
|
| 图 5 全景相机的核线误差示意图 Fig. 5 The epipolar errors of the two panoramic models |
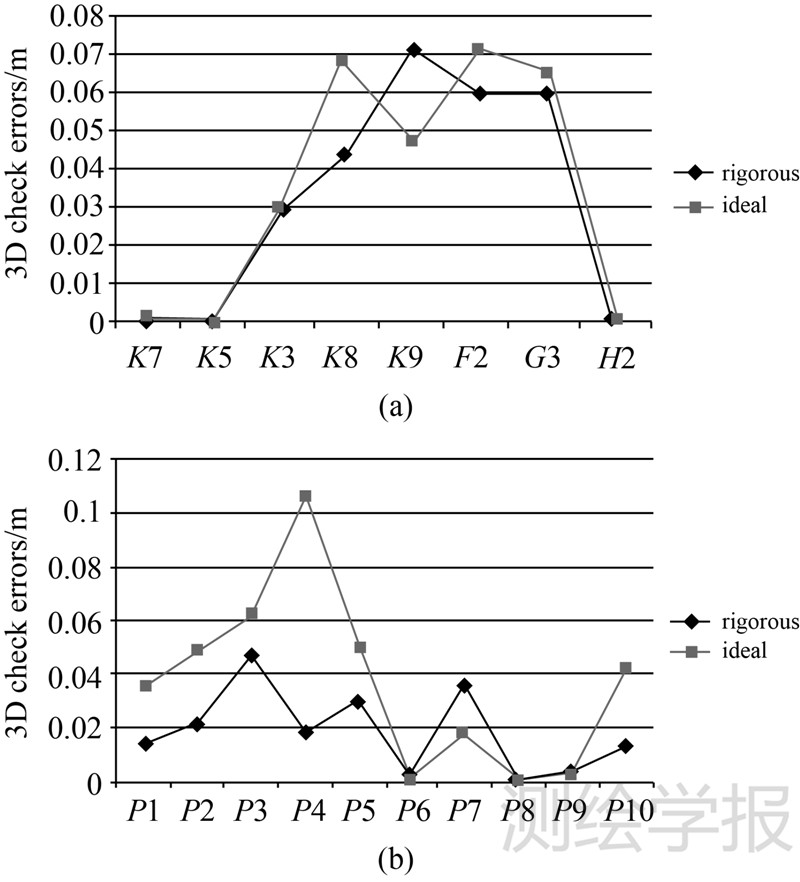
表 2显示了两种模型的光束法平差结果。在室外试验中,平差中误差(σ0)与EO的精度几乎一致,严格模型略优。全景影像的σ0约0.02m,看似与传统平面相机RMSE的微米级相差甚远,然而,20m处的等效像元大小约0.026m,这表示σ0优于1像素,因此同样符合传统意义上的像点量测精度。全景相机平差的另外一个特点是,σ0约等于3D前交的精度。这同样可由物距接近20m来解释,即物距约等于全景球面半径,即像距。图 6(a)显示了控制点残差。其中,点K7、K5和H2作为控制点,其余作为检查点;在理想模型中,检查点的平均3D定位误差是0.0568m,在严格模型中是0.0526m,两者基本一致。因此,根据表 2,可知室外试验中两个模型的差异可被忽略;该结论与式(7)的理论分析相符合:绝大多数特征点物像距离在-10~5m之间,使得最大误差不超过0.01m。因此所有连接点误差平差分配后,严格模型只有几个毫米的优势。
| 模型 | σ0/m | 外方位元素精度 | 3D交会误差/m | ||
| 线元素/m | 角元素/rad | ||||
| 理想 | 室外 | 0.0212 | 0.012 | 3.5×10-5 | 0.0214 |
| 严格 | 0.0198 | 0.012 | 3.7×10-5 | 0.0200 | |
| 理想 | 室内 | 0.0401 | 0.017 | 7.3×10-5 | 0.0412 |
| 严格 | 0.0210 | 0.011 | 4.5×10-5 | 0.0226 | |
|
| 图 6 光束法平差3D定位误差示意图 Fig. 6 3D localization check errors of the two panoramic models |
表 2也显示了室内数据两种模型的平差比较,σ0、EO精度和3D交会误差都有明显的差异。理想模型的σ0和3D交会误差约0.04m,是严格模型的两倍。图 6(b)显示了检查点残差,P6、P7和P9作为控制点,其余作为检查点。严格模型7个检查点的平均误差是0.0268m,而理想模型是0.0526m,表明室内试验中两种模型的定位结果非常明显。这主要是由于物距约3~8m,即物像距-17~12m,根据式(7)可知,当平均旋角为15°时,将产生约2cm的系统误差。这解释了理想模型的定位误差比严格模型低2cm。
与理想模型相比,严格模型在室内外的表现近乎一致,不受物距、旋角影响,反映了模型的精确性,唯一的区别是检查点的精度。室内检查点精度是0.0268m,与3D交会误差相符;而室外数据的检查点精度是0.05m,大于理论交会误差,这是由于室外GPS控制点的精度仅2cm,若采用高精度控制点,室外检查点精度将会得到提高。
5 结 论本文分析了一种广泛采用的全景理想成像模型的系统误差,并与严格成像模型作了室内外试验对比。室外试验说明,两种模型的差异微小,都适用于室外的车辆精确定位和3D测量。而室内试验说明,严格模型能够取得更高的定位精度和核线精度。两组试验的差异同时也支持了本文对理想模型误差规律的理论分析:定位误差随着物像间距与视角的增加而增大;核线误差随Z坐标和旋转角的增加而增大。
笔者推荐采用严格模型,尽管其稍复杂于理想模型。因为除了文中的分析,理想模型还有两个较大的缺点:首先,如果立体像对间的旋角过大,例如同名像点出现在0号和5号相机,则可能出现比本文理论分析更大的系统误差;其次,许多组合式全景相机的独立镜头投影中心与全景中心的距离Tr远大于4cm,根据式(4),这将导致比本文采用的Ladybug3相机更大的系统误差。
然而,全景理想模型在很多应用中也行之有效。首先,室外3D测量的结果与严格模型近乎相当。笔者也测试了长轨迹数千张车载全景影像的平差,两个模型的收敛性近乎一致。更重要的是,很多定位应用并不需要毫米、厘米级的摄影测量精度。如长距离车辆、机器人实时定位,其累计误差将达到数米甚至更高,几个厘米的系统误差完全可被忽略。这也是自动机器人、视觉SLAM等研究领域广泛采用理想模型的原因。
| [1] | ANGUELOV D, DULONG C, FILIP D, et al. Google Street View: Capturing the World at Street Level [J]. Computer, 2010, 43(6): 32-38. |
| [2] | XIAO Xiao. High Resolution Panoramic Imaging System and Visual Application [D]. Hangzhou:Zhejiang University, 2009. (肖潇. 高分辨率全景成像系统及其视觉应用研究[D].杭州: 浙江大学, 2009.) |
| [3] | YANG Shaoping, CHEN Xiong, KONG Qingsheng. Image-based Visual Serving for Mobile Robots with Central Panoramic Camera [J]. Computers Engineering and Design, 2010, 31(19):4261-4264. (杨少平,陈 雄,孔庆生. 采用全景相机的移动机器人视觉伺服[J]. 计算机工程与设计, 2010, 31(19):4261-4264.) |
| [4] | IKEDA S, SATO T, YOKOYA N. High-resolution Panoramic Movie Generation from Video Streams Acquired by An Omnidirectional Multi-camera System [C]// Proceedings of IEEE 19 International Conference on Multisensor Fusion and Integration for Intelligent Systems(MFI2003).[S.l.]:IEEE,2003:155-160. |
| [5] | MEI C, BENHIMANE S, MALIS E, et al. Efficient Homography-based Tracking and 3-D Reconstruction for Single-viewpoint Sensors [J]. IEEE Transactions on Robotics, 2008, 24(6): 1352-1364. |
| [6] | GEYER C, DANIILIDIS K. Catadioptric Projective Geometry [J]. International Journal of Computer Vision, 2001, 45(3): 223-243. |
| [7] | BARRETO P, ARAUJO H. Geometric Properties of Central Catadioptric Line Images and Their Application in Calibration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(1): 1327-1333. |
| [8] | PARIAN A, GRUEN A. Sensor Modeling, Self-calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65: 60-76. |
| [9] | SCHNEIDER D, MAAS H. A Geometric Model for Linear-array-based Terrestrial Panoramic Cameras [J]. Photogrammetric Record, 2006, 21(115): 198-210. |
| [10] | KAESS M, DELLAERT F. Probabilistic Structure Matching for Visual SLAM with A Multi-camera Rig [J]. Computer Vision and Image Understanding, 2010, 114(2): 286-296. |
| [11] | PAYA L, FERNANDEZ L, GIL A, et al. Map Building and Monte Carlo Localization Using Global Appearance of Omnidirectional Images [J]. Sensors, 2010, 10(12): 11468-11497. |
| [12] | GUTIERREZ D, RITUERTO A, MONTIEL J, et al. Adapting A Real-time Monocular Visual SLAM from Conventional to Omnidirectional Cameras [C]// Proceedings of the 11th OMNIVIS in IEEE International Conference on Computer Vision (ICCV).Barcelona:IEEE,2011:343-350. |
| [13] | SILPA ANAN C, HARTLEY R. Visual Localization and Loop-back Detection with A High Resolution Omni-directional Camera [C]//Workshop on Omnidirectional Vision and Camera Networks. [S.l.]: Omnivis,2005. |
| [14] | TARDIF J, PAVLIDIS Y, DANIILIDIS K. Monocular Visual Odometry in Urban Environments Using An Omnidirectional Camera [C]//Proceedings of IEEE/RSJ Conference on Intelligent Robots and Systems (IROS).[S.l.]:IEEE,2008:2531-2538. |
| [15] | JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94-100. (季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94-100.) |
| [16] | SHI Yun, JI Shunping, SHI Zhongchao, et al. GPS-supported Visual SLAM with A Rigorous Sensor Model for A Panoramic Camera in Outdoor Environments [J]. Sensors, 2013, 13(1): 119-136. |
| [17] | KANNALA J, BRANDT S. A Generic Camera Model and Calibration Method for Conventional, Wide-angle, and Fish-eye Lenses [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(8): 1335-1340. |
| [18] | SATO T, IKEDA S, YOKOYA N. Extrinsic Camera Parameter Recovery from Multiple Image Sequences Captured by An Omni-directional Multi-camera System [J]. Camera, 2004, 2: 326-340. |
| [19] | SATO T, YOKOYA N. Efficient Hundreds-baseline Stereo by Counting Interest Points for Moving Omni-directional Multi-camera System [J]. Journal of Visual Communication and Image Representation, 2010, 21(5-6):416-426. |
| [20] | LI Deren, ZHENG Zhaobao. Analytical Photogrammetry [M]. Beijing:Suveying and Mapping Publications, 1992. (李德仁, 郑肇葆. 解析摄影测量学[M]. 北京:测绘出版社, 1992.) |
| [21] | KANG Zhizhong, ZHANG Zuxun, YANG Fanlin. Relative Orientation and Epipolar Arrangement Based on Forward Moving Image Pairs along the Optical Axis [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 56-61. (康志忠, 张祖勋, 阳凡林. 基于沿主光轴方向摄影立体像对的相对定向与核线排列[J]. 测绘学报, 2007, 36(1): 56-61.) |