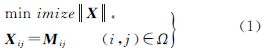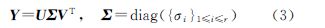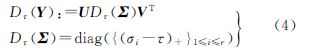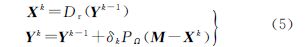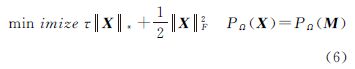2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences,Beijing 100049,China
1 引 言
在遥感影像形成和传输过程中,成像系统和设备的不完善以及大气的干扰等因素会使得图像质量退化。典型的遥感图像退化表现为图像模糊、有噪声、被云遮挡和细节信息缺损等。图像复原即对退化的图像质量进行改善的过程,其对后续的图像分析与理解有重要的指导作用。遥感图像复原中的去噪问题一直是图像处理领域的研究热点,而对于大气中的云雾遮挡问题,当前也缺乏简单有效的去除方法。近几年来,在机器学习、工程控制和计算机视觉等研究领域,利用非常有限的元素来恢复未知的低秩或近似低秩矩阵也即矩阵填充(matrix completion,MC)迅速发展成为新的研究热点[1, 2]。
目前的图像去噪研究主要集中在非线性滤波处理,其中偏微分方程(partial differential equation,PDE)类方法因局部自适应能力强、灵活性与稳定性好及模型扩展方便等优点,成为近些年相关研究的热点。文献[3]将非线性扩散方程引入到图像处理领域,提出了著名的P-M方程(Perona-Malik equation),其将图像滤波与边缘检测统一起来,对PDE在图像处理中的应用具有重大的推动作用。文献[4]提出了一种纯各向异性扩散方程,该改进的模型对椒盐类孤立噪声具有很好的去除效果,但在平滑区会过度扩散。针对低阶非线性PDE易产生阶跃效应和过度平滑的缺陷,文献[5]提出了4阶PDE去噪模型,但其不能有效保留边缘信息。为了在去噪的同时保留边缘,文献[6]用BV(bonnded variation)空间的半范数-全变分作为正则项提出了全变分(total variation,TV)模型,但其存在易产生阶跃效应及对纹理敏感等不足。文献[7]提出了一种能够保持图像纹理的自适应保真去噪模型,其通过构造对数值保真项的加权函数,在全变分的模型下引入自适应保真项。为更好地处理纹理,文献[8]提出了非局域均值(non-local means)滤波,文献[9]通过提出非局域正则化函数形成了一种NL-means变分框架。
在影像修复方面,文献[10]使用各向异性热传导模型,同时将图像的结构和纹理信息进行扩散来修复图像。此外,文献[11]利用小波框架来进行图像盲修复,在检测图像中坏像元或噪声点的同时修复影像。文献[12]提出了基于Bandelet变换的图像修复法进行遥感去云,但此法依赖于影像不同区域的几何流曲线特征表达的结果,且对较大面积云覆盖区的修复能力不足。
以影像融合法[13]为代表的基于序列影像的去云方法,需要同一区域的多源影像,且要求影像间的云区不重叠并解决可能存在的辐射差异问题,这些限制了其实用性。文献[14]提出了基于支持向量机的遥感影像厚云去除法,但仍需同一区域的多源影像,且需进行修复后处理。因此,仅利用原始图像中部分已知信息,对缺损信息进行修补的单幅影像去云修复具有更实际的研究价值。
由于地学信息具有地理时空相关性,在很多情况下,遥感影像中的局部或大部分区域存在结构内容或纹理等相似性,这使得影像矩阵块呈现低秩或近似低秩的现象,也为矩阵填充理论在遥感图像处理中的应用提供了保证。基于此,本文提出一种基于矩阵填充的遥感影像低秩信息恢复方法,并进行了影像的椒盐噪声去除及厚云修复研究。
2 矩阵填充理论及算法矩阵填充问题可以被简单地描述为:对于一个未知的矩阵M∈RN1×N2,若已知其中m个采样矩阵元{Mij:(i,j)∈Ω},这里Ω为从矩阵M的N1×N2个矩阵元位置中随机采样的一个基数为m的矩阵元位置集合,由少量元素{Mij}来恢复出整个矩阵M中所有元素的问题即为MC问题。
2.1 MC理论简述MC问题是一个非适定性问题,在没有额外的信息约束下,这意味着有无数个填充的矩阵结果。然而,当未知矩阵为低秩或近似低秩时,这就改变了问题的性质,使得精确重构原矩阵有了可能。
文献[1]中,即便仅有极少量的采样元素,绝大多数低秩矩阵也能够被精确恢复,而且这种恢复可以通过求解下式的凸优化问题达到
式中,||·||*表示矩阵的核范数;M为部分元素缺失的未知矩阵;X为待填充矩阵M的最优逼近解。设M∈RN×N且矩阵秩为r,当已知元素的采样数m满足m≥CN6/5rlogN(C为正的常数值)时,矩阵M能够被完美地恢复出来。
2.2 奇异值阈值收缩算子对于式(1)给出的核范数最小化问题的求解,文献[2]提出了奇异值阈值收缩算法(singular value thresholding,SVT)来解决大型低秩矩阵的填充重构问题。
设PΩ为作用于矩阵空间子集Ω上的正交投影算子,可以将式(1)表达为
min imize||X||* PΩ(X)=PΩ(M)
式中
式中,X∈RN1×N2为待重构矩阵M∈RN1×N2的最优逼近解。
对于秩为r的矩阵Y∈RN1×N2,设其奇异值分解形式为
式中,U∈RN1×r,V∈RN2×r,其列向量为规范正交向量;其中奇异值序列{σi}1≤i≤r降序排列。给定阈值τ>0,引入软阈值算子Dτ
式中,(·)+=max(0,·),即向量或矩阵的正数部分。这种算子对奇异值应用软阈值规则,使其有效地向零收缩,进而使得Dτ(Y)的秩相对Y的秩较低,它是与核范数相关联的最接近算子。
给定一个正步长序列{δk},初始化Y0=0∈RN1×N2,对于k=1,2,…,n引入收缩迭代
求解式(5)所得的解序列{Xk}收敛于凸优化问题的唯一解,而且当τ→∞时,式(6)的解收敛于式(2)的解。因此,通过选择较大的τ值,收缩迭代序列会收敛于式(1)的最优逼近解。式中,||·||F表示矩阵的Frobenius范数。
3 基于MC的低秩信息重构复原法矩阵填充解决的是利用少量的采样/已知矩阵元数据来精确地重构原始完整的未知矩阵信息的问题,而图像复原中的去噪/去云修复等问题也是针对图像矩阵因被污染或遮挡等造成的数据缺损来进行原始影像的重构恢复。基于此,本文提出一种基于MC的影像低秩信息复原方法。
3.1 低秩性与数据采样矩阵填充的前提是所恢复的矩阵必须是低秩或近似低秩,而这种要求在图像中具体表现为图像矩阵块中的灰度信息相似或影像结构纹理规则突出等特性。在遥感影像中,由于地学信息具有地理时空相关性,在很多情况下,影像中的局部或大部分区域存在结构内容或纹理相似性等现象,这使得影像局部矩阵块呈现低秩或近似低秩的状态。
对于秩为r的矩阵X∈RN1×N2,其自由度为dr:=r(N1+N2-r),要确定整个矩阵X,必须至少已知其中dr个矩阵元。通常,为保证数据采样的合理性,一般选取随机采样,且采样元素数量m也需满足前述的条件。
3.2 参数设定与“热启动”技术初始参数的设定对算法执行的效能影响较大,在SVT算法中,比较关键的两个参数为步长{δk}以及阈值τ。文献[2]证明了当步长序列遵循0<infδk≤supδk<2时,由式(5)获得的解序列{Xk}收敛于式(6)中的唯一解。
较大的阈值τ会使得求解精度高,但会降低算法的收敛速度。为兼顾阈值参数τ初值选取的合理性与算法求解的高精度,本文设计了一种参数“热启动”的连续性方案:构造一个升序排列的τ值序列τ0、τ1、τ2、…、τi利用对τ=τi-1时凸优化问题式(6)的求解值作为初始估计值来进行τ=τi时凸优化问题的求解。相对于直接使用一个固定的较大τ值进行求解的“冷启动”技术,这种策略更科学合理,且算法收敛更快、求解精度更高。
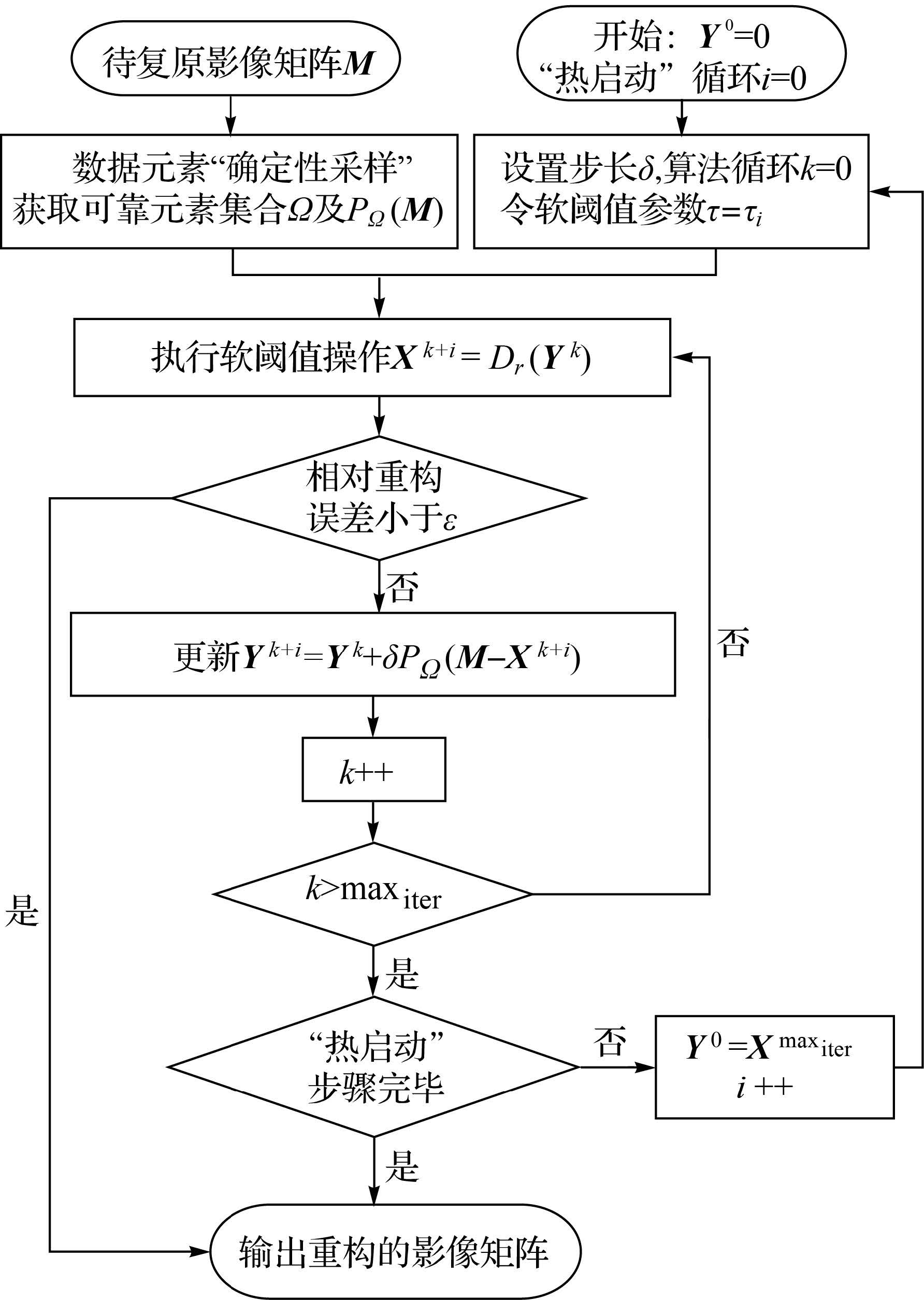
3.3 本文算法实现流程<br> 在获取采样矩阵元并设定好初始参数后,即可利用SVT算法进行收缩迭代重构原始影像矩阵信息。当相对重构误差小于给定的容忍误差即||PΩ(Xk-M)||F/||PΩ(M)||F≤ε或迭代次数达到最大迭代次数maxiter时,算法停止迭代,输出重构结果。主要流程图如图 1所示。
|
| 图 1 本文算法主要流程 Fig. 1 Main disposal flows of arithmetic proposed in the paper |
本文采用Matlab作为工具,在3.10 GHz频率的双核CPU以及3 GB内存配置下的计算机上进行了遥感图像低秩信息复原试验。此部分首先选取了满足低秩条件的Mondrian格子图与纹理规则突出的Barbara图,分别用于自然图像的椒盐噪声去除与图像修复试验,进而再推广到遥感影像中进行去噪复原与去云修复。同时引入峰值信噪比(dB)与感知结构相似度(structural similarity,SSIM)分别作为客观评价指标与主观视觉评价标准。
4.1 图像低秩信息去噪恢复试验经过前期校正后,一般认为遥感图像中所含噪声为高斯噪声和椒盐噪声的叠加[15],本部分通过试验分析了MC在图像椒盐噪声去除应用方面的优势及关键问题。对原始矩阵元素的采样是MC能够有效恢复图像信息的关键,采样元素最好为被污染或破坏程度较小的高可信数据;同时,考虑到椒盐噪声本身即具备随机性,本试验进行“确定性采样”以获取可靠采样元。椒盐噪声在图像上表现为极高灰度或极低灰度噪声点,其具有两个明显的特征:灰度值非常大或非常小;与邻域信号点灰度值相差较大。本试验综合利用这两个特征,采用“灰度阈值采样法”结合“中值试探采样法”进行确定性采样:灰度阈值法,即设置阈值α,并将灰度值处于区间255-α,255或0,α的像元作为候选噪声点;中值试探法,即将邻域窗口像素灰度中值与当前候选噪声点灰度差值的绝对值大于规定阈值β的当前像元视为噪声点。最后将非噪声点像元作为相对可靠数据来进行后续的信息重构。
如图 2(a)所示,原始Mondrian影像内部结构内容相似度较高,而图 2(b)则加入了密度为0.1的椒盐噪声,图 2(j)为MC去噪效果图。作为对比,本文选取了已有的各种典型滤波算法进行了椒盐噪声去除试验,如图 2(c)—(i)。从图中可见,TV去噪、形态学滤波、自适应中值滤波及纯各向异性扩散法虽能够较好地去除噪声,但前三者因涉及窗口尺寸问题会滤除部分边缘细节信息,后者甚至因平滑区过度扩散而模糊掉了边界。然而,MC去噪则可以很好地解决此类问题,在图像矩阵秩非常低的情况下,能够近乎完美地重构原图像。表 1则给出了各种方法去噪的PSNR与SSIM指标对比结果,同样表明,MC对椒盐噪声的去除能力近乎达到最优,其在去噪效能及图像结构信息保持方面要优于其他方法。

|
| 图 2 Mondrian图像去噪恢复试验 Fig. 2 Denoising experiments on Mondrian image |
| 图像 | 统计 指标 | 含噪 影像 | TV 去噪 | NL- means | 四阶 PDE | 方向 扩散 | 形态学 滤波 | 小波 软阈值 | 自适应 中值 | MC 重构 |
| 蒙德 | PSNR | 14.691 | 28.249 | 20.197 | 18.474 | 19.522 | 27.176 | 19.670 | 22.594 | 55.656 |
| 里安 | SSIM | 0.779 | 0.989 | 0.916 | 0.875 | 0.912 | 0.986 | 0.903 | 0.958 | 1.000 |
| 遥感 | PSNR | 14.967 | 25.329 | 24.239 | 21.255 | 23.890 | 23.309 | 23.235 | 30.793 | 35.724 |
| 影像 | SSIM | 0.431 | 0.872 | 0.834 | 0.722 | 0.809 | 0.816 | 0.821 | 0.967 | 0.990 |
以下则给出了MC重构对遥感图像中椒盐噪声去除的试验,图 3为各种去噪方法在WorldView-2高分辨率遥感影像中去除椒盐噪声(密度为0.1)的结果图,对应的遥感影像去噪统计指标见表 1。由图可知,MC重构与自适应中值滤波去噪效果要明显好于其他方法,且对影像纹理细节信息保持得较完美。TV法与形态学去噪不够彻底,且仍存在对边缘细节信息保存不完美的缺陷。由表 1可知,MC重构法要略胜于自适应中值滤波。

|
| 图 3 WorldView-2影像椒盐噪声去除试验 Fig. 3 Experiments of removal of salt & pepper noises on WorldView-2 image |
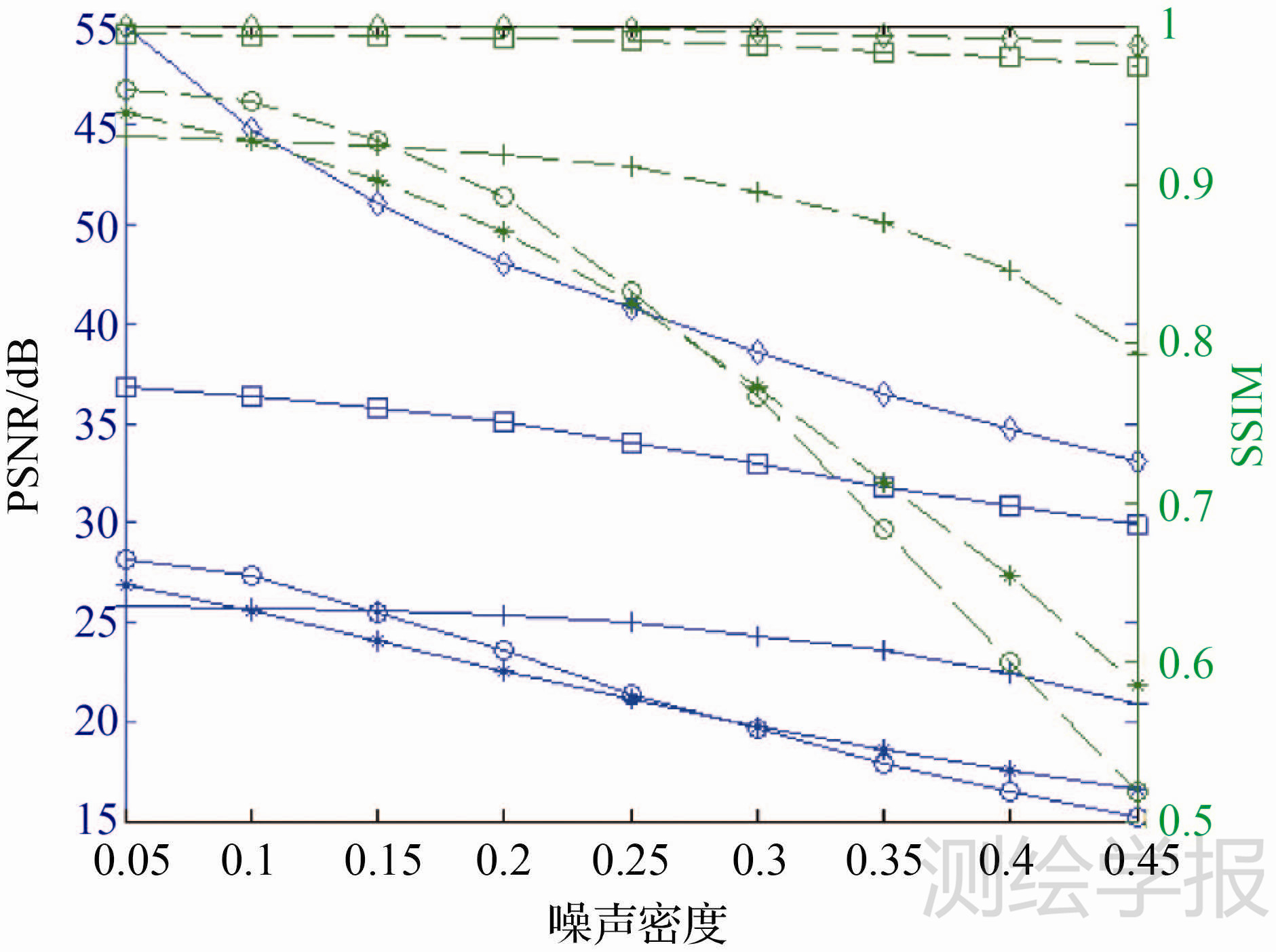
为进一步表明本文算法在遥感影像椒盐噪声去除中的优越性,另选取了一幅建筑物结构规整的遥感影像进行试验,图 4展示了椒盐噪声密度为0.2时几种算法去噪的结果图。图 5则给出了各种算法去噪的性能指标随噪声密度变化的趋势图,此双坐标轴图中蓝色实曲线与绿色虚曲线则分别记录着各种算法的PSNR与SSIM值,带有菱形、方形、加号、圆圈、星号标识的曲线则分别对应着MC重构法、自适应中值滤波、纯各向异性扩散法、TV去噪与NL-means滤波法。结果表明,在任何噪声密度下,MC重构去噪效果要好于其他算法 。试验发现:在噪声密度较大时,为保证算法恢复性能较好,MC重构的中值试探采样法的邻域窗口也应适当变大。

|
| 图 4 噪声密度为0.2时各种算法去噪结果 Fig. 4 Denoising results of different algorithms when the density of noises is 0.2 |
|
| 图 5 各种算法去噪性能与噪声密度关系 Fig. 5 The relationship between denoising performance and density of noise |
图像修复是图像复原中的新方法,其利用破损图像中的已知信息,根据一定的算法对缺损区域进行修补,以达到视觉上合理的效果。图 6给出了基于MC的图像修复法对Barbara图中的纹理信息进行复原的结果,并选用小波和全变分修复法作为对比,待修复影像中有两块黑色和一块白色区域中的信息被掩盖掉;而图 7则是对图 6中白色区块所遮挡的纹理信息进行修复的局部放大图,其中利用小波变换、TV和MC修复法进行纹理信息恢复的统计指标分别为:PSNR(23.174 dB,24.194 dB,27.600 dB),SSIM(0.859,0.885,0.952)。结果表明,MC修复法能够较完美地恢复影像纹理信息,保持图像结构的连贯性,避免了小波与TV修复法中的块效应。

|
| 图 6 各种方法对Barbara纹理图修复结果 Fig. 6 Inpainting results of textures in Barbara image by different methods |

|
| 图 7 各种方法修复局部图 Fig. 7 Local parts of inpainting results using different methods |
由于MC在低秩信息恢复中具有很强的优势,当缺损信息块较大时,低秩影像数据也能近乎完美地重构修复出来,如图 8给出的是遥感海表温度(sea surface temperature,SST)反演产品的去云修复试验。图 8(a)提供的数据为由Aqua卫星MODIS传感器所获数据的SST图,图上白色斑块为受云污染而造成的温度值缺损块,图 8(b)为利用冷启动MC去云修复的结果,图 8(c)-(e)则给出的为热启动MC去云修复结果序列图。这里,数据采样是将影像中受云污染而造成的温度值缺损像元排除在有效采样数据之外。由图知,热启动技术MC去云修复的效果要明显好于冷启动技术,基本能将云区有效去除且同时复原SST数据。热启动技术首先利用较小的τ=1500求解一个粗解,其精度不如冷启动技术中直接选用较大τ=2500所获得的解;然而,热启动技术第2轮循环利用τ=2000所获解的精度就已高于冷启动技术;当循环到τ=2500时,已能近乎精确地重构SST图。这主要是因为,冷启动技术仅仅使用一个固定的阈值参数τ及预先给定的无先验知识的原始图像矩阵初始值Y0,这种方法显得盲目且不合理;热启动技术利用前一次循环重构出的图像信息值作为下一次循环重构的初始值,能够使重构精度更高,算法收敛速度更快。

|
| 图 8 遥感SST反演产品中厚云去除修复试验 Fig. 8 Clouds removal of SST retrieval product |
为了更好地验证本文基于MC的图像修复技术在遥感影像厚云去除中的有效性,本文又选取了一幅含有厚云的SPOT5高分辨率遥感影像进行去云修复的试验。对比可知,基于MC的去云修复法能够较好地恢复地物信息,并保持影像结构的连贯性。

|
| 图 9 高分辨率遥感影像厚云去除试验 Fig. 9 Removal of thick clouds from high-resolution RS image |
本文提出了一种新颖的基于矩阵填充的遥感影像复原方法,通过“确定性采样”方案获取影像矩阵中的可靠性像元数据,在热启动技术支持下利用奇异值阈值法求解一个凸优化问题,最后重构出待恢复的影像信息。通过将本文方法用于图像椒盐噪声去除复原及遥感厚云去除修复试验,结果表明,该法能较好地复原图像中的边缘细节及纹理信息,特别在原始影像矩阵具备低秩或近似低秩性时,重构复原的性能近乎达到最优。由于矩阵填充能够从少量矩阵采样数据中较好地重构出原始低秩矩阵,其在遥感低秩信息处理、图像压缩及地学时空相关数据重构等地学与测绘遥感领域也具有应用潜力。
| [1] | CANDES E J, RECHT B. Exact Matrix Completion via Convex Optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772. |
| [2] | CAI J, CANDES E J, SHEN Z. A Singular Value Thresholding Algorithm for Matrix Completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. |
| [3] | PERONA P, MALIK J. Scale-space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639. |
| [4] | ALVAREZ L, MOREL J M. Formalization and Computational Aspects of Image Analysis[J]. Acta Numerica, 1994(3): 1-59. |
| [5] | YOU Y L, KAVEH M. Fourth-order Partial Differential Equations for Noise Removal[J]. IEEE Transactions on Image Processing, 2000, 9(10): 1723-1729. |
| [6] | RUDIN L, OSHER S, FATIMI E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physisca D, 1992, 60: 259-268. |
| [7] | GILBOA G, SOCHEN N, ZEEVI Y Y. Variational Denoising of Partly Textured Images by Spatially Varying Constraints[J]. IEEE Transactions on Image Processing, 2006, 15(8): 2281-2289. |
| [8] | BUADES A, COLL B, MOREL J M. A Non-local Algorithm for Image Denoising[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE, 2005:60-65. |
| [9] | GILBOA G, OSHER S. Nonlocal Operators with Applications to Image Processing[J]. SIAM Journal on Multiscale Modeling and Simulation, 2008, 7(3): 1005-1028. |
| [10] | QIN C, WANG S Z, ZHANG X P. Simultaneous Inpainting for Image Structure and Texture Using Anisotropic Heat Transfer Model[J]. Multimedia Tools and Applications, 2012, 56(3): 469-483. |
| [11] | DONG B, JI H, LI J, et al. Wavelet Frame Based Blind Image Inpainting[J]. Applied and Computational Harmonic Analysis, 2012, 32(2): 268-279. |
| [12] | MAALOUF A, CARRE P, AUGEREAU B, et al. A Bandelet-based Inpainting Technique for Clouds Removal from Remotely Sensed Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 2363-2371. |
| [13] | GABARDA S, CRISTOBAL G. Cloud Covering Denoising through Image Fusion[J]. Image and Vision Computing, 2007, 25: 523-530. |
| [14] | LIANG Dong, KONG Jie, HU Gensheng, et al. The Removal of Thick Cloud and Cloud Shadow of Remote Sensing Image Based on Support Vector Machine[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 225-231,231,238. (梁栋,孔颉,胡根生,等. 基于支持向量机的遥感影像厚云及云阴影去除[J]. )测绘学报,2012,41(2):225-231,238. |
| [15] | WANG Xianghai, ZHANG Hongwei, LI Fang. A PDE-based Hybrid Model for De-noising Remote Sensing Image with Gaussian and Salt-pepper Noise[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 283-288. (王相海,张洪为,李放. 遥感图像高斯与椒盐噪声的PDE混合去噪模型研究[J]. )测绘学报,2010,39(3):283-288. |
| [16] | LIU Z, VANDENBERGHE L. Interior-point Method for Nuclear Norm Approximation with Application to System Identification[J]. SIAM Journal on Matrix Analysis and Applications, 2009, 31(3): 1235-1256. |
| [17] | BERTALMIO M, SAPIRO G, CASELLES V, et al. Image Inpainting[C]//Proceedings of ACM SIGGRAPH.Chicago: ACM, 2000: 417-424. |
| [18] | ZHANG Z, GANESH A, LIANG X, et al. TILT: Transform Invariant Low-rank Textures[J]. International Journal of Computer Vision, 2012, 99(1): 1-24. |
| [19] | JI H, LIU C, SHEN Z, et al. Robust Video Denoising Using Low Rank Matrix Completion[C]//Proceedings of IEEE Conference on CVPR.[S.l.]:IEEE, 2010: 1791-1798. |
| [20] | YIN W, OSHER S, GOLDFARB D, et al. Bregman Iterative Algorithms for l1-minimization with Applications to Compressed Sensing[J]. SIAM Journal on Imaging Science, 2008, 1(1): 143-168. |
| [21] | ZHANG H, CHENG L, ZHU W. Nuclear Norm Regularization with a Low-rank Constraint for Matrix Completion[J]. Inverse Problems, 2010, 26(11): 115009-115023. |
| [22] | ELAD M, STARCK J L, QUERRE P, et al. Simultaneous Cartoon and Texture Image Inpaiting Using Morphological Component Analysis (MCA) [J]. Applied and Computational Harmonic Analysis, 2005, 19(3): 340-358. |
| [23] | LI Zhidan, HE Hongjie, YIN Zhongke, et al. Adaptive Image Inpainting Algorithm Based on Patch Structure Sparsity[J]. Acta Electronica Sinica, 2013, 41(3): 549-554. (李志丹,和红杰,尹忠科,等. 基于块结构稀疏度的自适应图像修复算法[J]. )电子学报,2013,41(3):549-554. |
| [24] | JUNG M, BRESSON X, CHAN T F, et al. Nonlocal Mumford-Shah Regularizers for Color Image Restoration[J]. IEEE Transactions on Image Processing, 2011, 20(6): 1583-1598. |
| [25] | CANDES E J, TAO T. The Power of Convex Relaxation: Near-optimal Matrix Completion[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2053-2080. |
| [26] | ERIKSSON A, VAN DEN HENGEL A. Efficient Computation of Robust Low-rank Matrix Approximations in the Presence of Missing Data Using the l1-norm[C]//Proceedings of IEEE Conference on CVPR.[S.l.]:IEEE,2010: 771-778. |