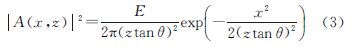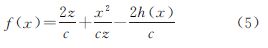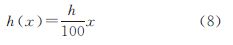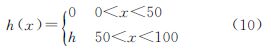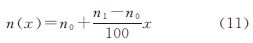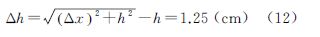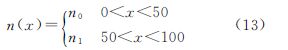1 引 言
随着世界科技的快速发展,传统的卫星光学成像技术、星载SAR成像技术由于受到气候条件、光照条件影响及自身波段限制,分辨率和高程测量精度难以进一步提高,已不能满足全球精确测绘的需要(如绘制1∶10 000和1∶5000比例尺地图)[1, 2, 3, 4]。激光技术与雷达技术结合产生的主动式传感器——激光雷达,具有不受国界限制、全天时全天候工作、高灵敏度、高分辨率、高测距精度的特点,因而受到了航空航天测绘领域的广泛研究和应用[5, 6, 7, 8, 9, 10],在地球极地冰盖探测、地表植被探测以及海洋探测中展示出了出色的高程测量能力,并且已经成功应用于月球、水星和火星的高程测量中[11, 12, 13]。
星载激光雷达发散角较小(通常为几十微弧度),但由于其轨道高度大(400~1000 km),因此在地面形成的光斑一般为10~200 m。激光足印区域地形的起伏、地貌的分布对激光回波信号的时间、空间分布有很大影响,相当于对入射的激光脉冲进行了时间-空间调制[14],而回波信号的波形直接影响高程测量的精度。目前,关于激光雷达测绘性能的研究大多只针对机载试验与仿真[15, 16, 17],针对星载激光雷达三维测绘的研究还比较少,尤其是Geiger模式的单光子探测技术在航天测绘领域中的应用可行性及性能还未得到充分研究[18]。本文首先介绍了激光三维测绘卫星高程测量的原理,并对不同地形、地貌建立物理模型,通过仿真手段得到了经过地表形貌调制后的脉冲波形的时间-空间分布,最后采用蒙特卡罗方法研究了不同地表形貌对Geiger探测模式的星载激光雷达测量精度的影响,并利用Matlab生成仿真DEM数据,对激光三维测绘卫星的测绘效果进行了仿真试验验证。
2 基于Geiger探测模式的星载激光雷达测高原理 2.1 激光雷达脉冲信号回波数学模型星载激光三维成像雷达探测流程如图 1所示。首先由激光发射器向探测目标地点发射激光脉冲,激光脉冲在经过大气衰减后到达地表反射区域并发生漫反射,被反射的激光回波再经过大气衰减后进入到激光探测器中。

|
| 图 1 星载激光三维成像雷达卫星测量示意图 Fig. 1 The surveying scheme of space borne 3D LiDAR |
图 1中,T为大气单程透过率,n(x,y)为地面反射率分布函数,f(x,y)为地形分布函数,H为卫星轨道高度。在脉冲往返时间(几个毫秒)内,卫星会飞行一定距离(几十米),实际激光脉冲经过的路程与垂直高度往返会有一定偏差,可以证明,卫星飞行在此段时间引起的高程测量误差很小,可以忽略。
在不考虑大气对脉冲的影响情况下,激光雷达回波信号可以看作源信号经过往返两次菲涅尔衍射过程和一次地表漫反射过程得到。激光脉冲的发射源信号一般表达式为
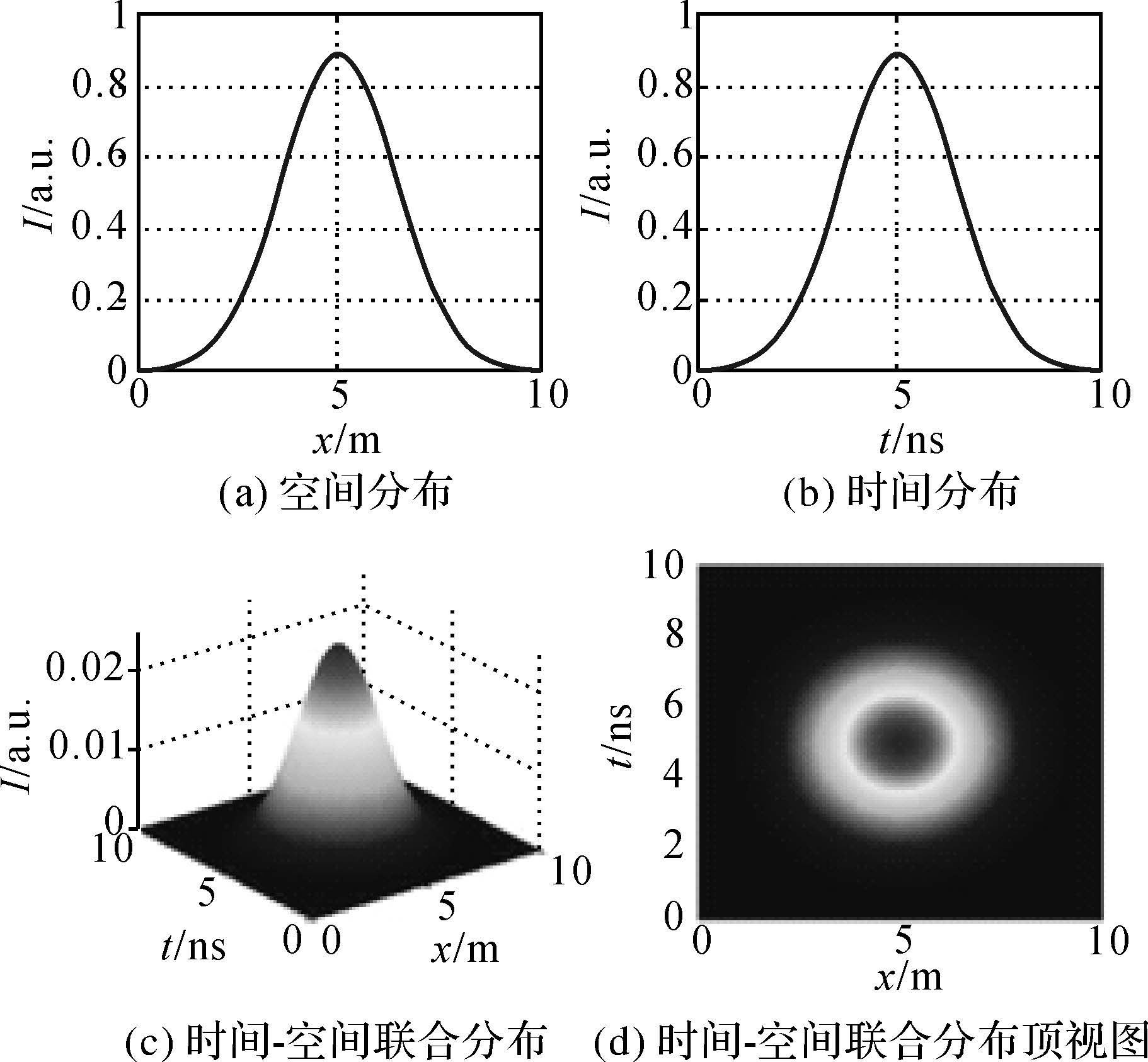
式中,A0为振幅;σpulse为激光脉宽;z为传播距离;θ为激光发散角。垂直于传播方向应为二维(x,y)分布,且x、y方向完全等价,这里为了方便仅选取x方向的一维模式。发射脉冲的时间、空间分布及其联合分布如图 2所示。
|
| 图 2 激光脉冲的时间、空间分布特性 Fig. 2 Temporal and spatial distribution of laser pulse |
可以看出,发射的激光脉冲在时间、空间维度上均为高斯分布模型。根据C.S.Gardner的反射回波理论[19],可以得到回波信号表达式
式中,S为激光探测器光学口径;T为单程大气透过率;n(x)为地表反射率分布函数;A(x,z)、g(t)、f(x)分别为激光传播到z处足印振幅分布、激光脉冲时域分布和地表形状分布函数,表达式分别为
式中,E为单位脉冲能量;h(x)为地表相对起伏。
2.2 Geiger模式信号探测原理对于普通的激光测高仪,一般采用单点式、低重频测量模式,发射功率为几十毫焦,如ICESat卫星[11, 20],但对于激光三维测绘卫星,需要获得全球全覆盖的高程信息,因此要求足印较小,重复频率需达到千赫量级,且采用千元激光脉冲阵列发射模式。受限于卫星的电源输出功率,每个脉冲的能量为几百微焦量级甚至更小。理论估算可知,在1.5 m左右的探测口径条件下,回波能量约为10-18 J,达到单光子量级,因此传统的线性探测模式已然不适用于激光三维测绘卫星,必须采用光子计数体制实现回波弱信号的探测。Geiger模式APD探测器可以达到单光子级的探测灵敏度,使得以Geiger模式探测器为基础的测距系统具有远距离测距的优势[21, 22],因此在激光三维测绘卫星中,选取Geiger模式的APD探测器实现单光子信号探测。
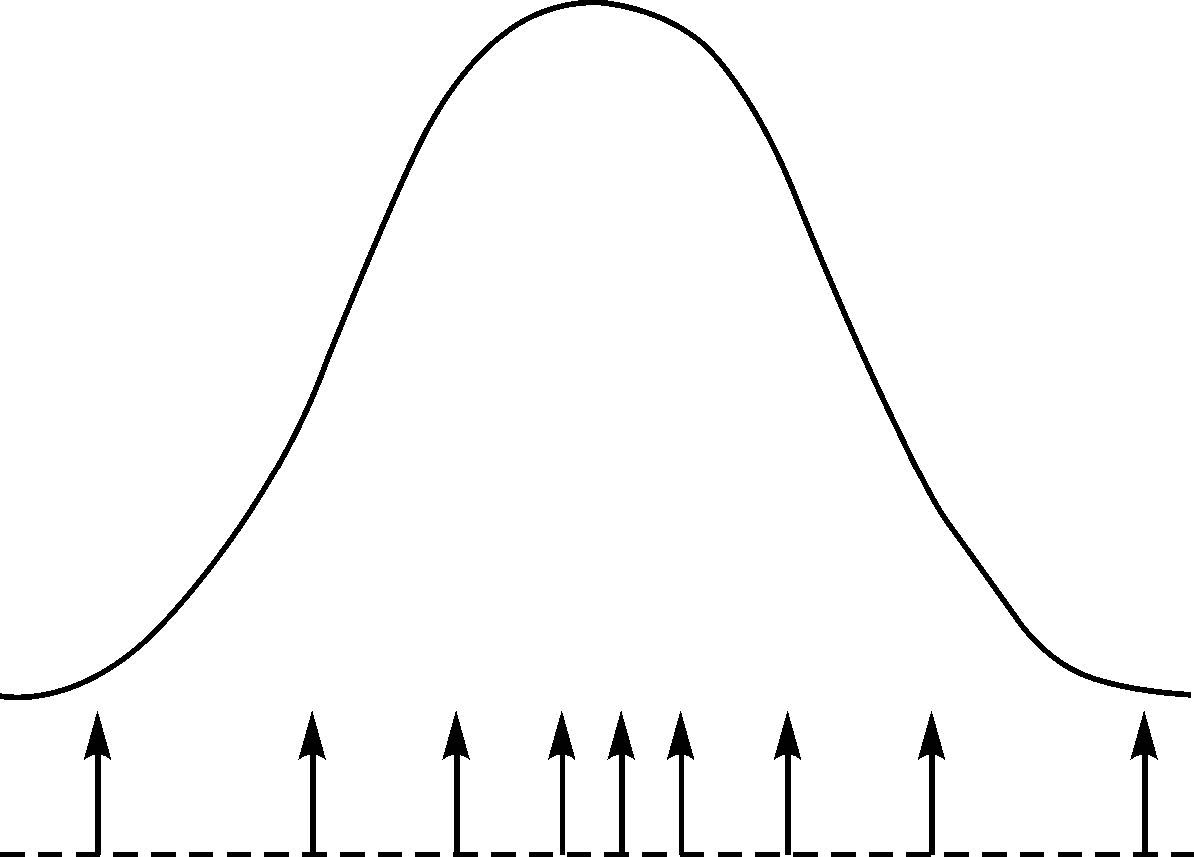
如图 3所示,由于回波光子数少,回波信号成为不连续的光子分布,回波信号强的区域(波峰)对应的光子分布概率大(分布密集),回波信号弱的区域(波腹)对应的光子分布的概率小(分布稀疏)。当APD处于Geiger探测模式下时,每当探测到一个光电子便能产生雪崩饱和,输出一次探测结果。与传统线性探测模式相同,Geiger探测模式同样采用记录脉冲发射与回波时间间隔来测量距离,测距公式为
|
| 图 3 单光子探测回波信号与连续波信号关系示意图 Fig. 3 Echo pulses from single-photon-detection and normal continuous LiDAR detection |
不同的是,线性探测模式采用的是质心法或阈值法来确定回波脉冲的时刻,而Geiger模式在一次探测中只能采集到一个回波信号,这个时刻便认为是回波时刻。
由于回波光子数服从Poisson分布,Geiger模式下光电子探测的概率为[8]
式中,N为回波光电子数,当信号和噪声同时存在时,N=Nsignal+Nnoise。需要指出的是,Geiger探测模式下,无法区分探测到信号的是噪声还是回波信号,存在虚警问题,可以利用相关硬件、软件方法,如距离门控制、滤光衰减法、多脉冲探测等方法降低虚警概率[23, 24],这里不作过多说明。
采用蒙特卡罗方法仿真Geiger模式探测过程思路为:将选通距离门以硬件计时精度为间隔划分为一系列独立的时间区间;依次计算每个区间被触发的概率并与生成的随机数比较,直到探测器被触发输出触发时间。算法流程如图 4所示。多次重复以上过程,以输出时间的平均值作为回波时间。

|
| 图 4 单光子探测回波时刻仿真算法流程图 Fig. 4 The flow diagram of simulation algorithm of single-photon-detection |
在仿真计算过程中,选取的相关参数如表 1所示。
| 参量 | 数值 |
| 卫星轨道高度H/km | 400 |
| 地表反射率n | 0.2 |
| 激光足印直径d/m | 10 |
| 激光脉宽σpulse/ns | 10 |
| 选通距离门t/μs | 4 |
| 平均回波光电子数N | 5 |
| 仿真重复次数 | 105 |
通常来说,即使激光足印直径为几十米,地面形状起伏、反射率也具有复杂的分布。这里笔者将足印内的地表抽象成4种数学-物理模型:斜坡地形、台阶地形、植被地貌(反射率的“斜坡”分布)和分界地貌(反射率的“台阶”分布),如图 5所示,其他复杂地形、地貌可以表示为简单模型的组合、叠加[14]。

|
| 图 5 4种地形地貌物理模型 Fig. 5 4 models of geography and geomorphology |
斜坡地形模型中,地表起伏分布为
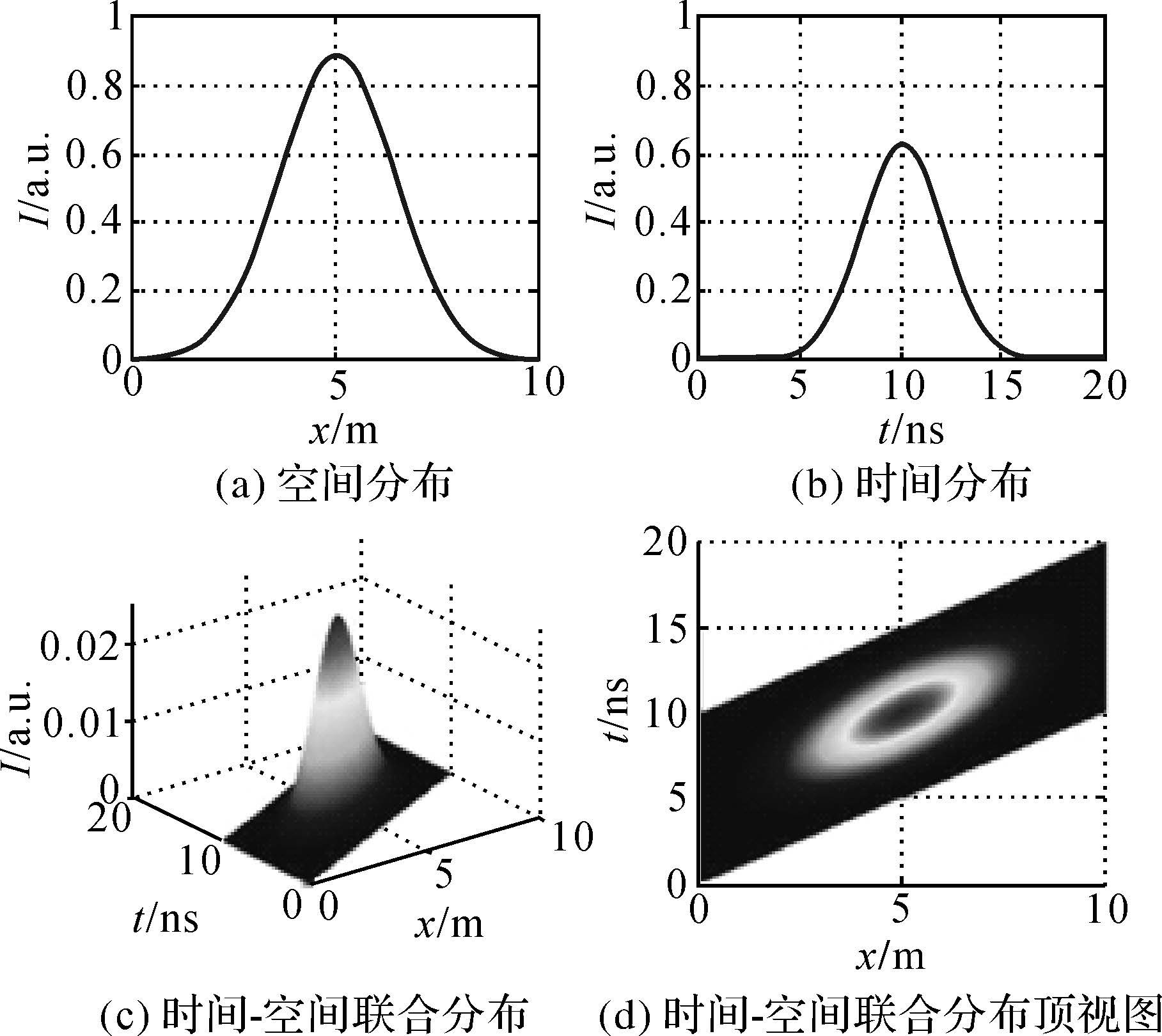
定义斜坡地形高度真实值为斜坡的平均高度,即斜坡高度的一半。斜坡地形下,激光脉冲回波的时间、空间分布如图 6所示。
|
| 图 6 斜坡地形回波信号的时间、空间分布特性 Fig. 6 Temporal and spatial distribution of echo pulse from slope terrain |
从图 6可以看到,斜坡地形不影响回波信号的空间分布,但信号回波时间随地表高度的变化有一定延时,延时的结果是脉冲被展宽。
图 7(a)给出了回波信号波形随斜坡高度变化的关系:随着斜坡高度的增加,脉冲宽度逐渐增大,且波峰位置也在逐渐右移。从图 7(b)可以看出,随着坡度变陡,波峰位置移动,仿真得到的探测高度值也逐渐增加,且满足关系
这正是斜坡中心高度的表达式,因此探测到的h值是平均高度的无偏测量。但由于脉宽的加大,探测值的标准差也与tan θ成正比增加。

|
| 图 7 斜坡回波信号波形及测量精度与斜坡倾角的关系 Fig. 7 Relationship between echo pulse,detection precision and dip angle of the slope |
台阶地形模型中,地表起伏分布为
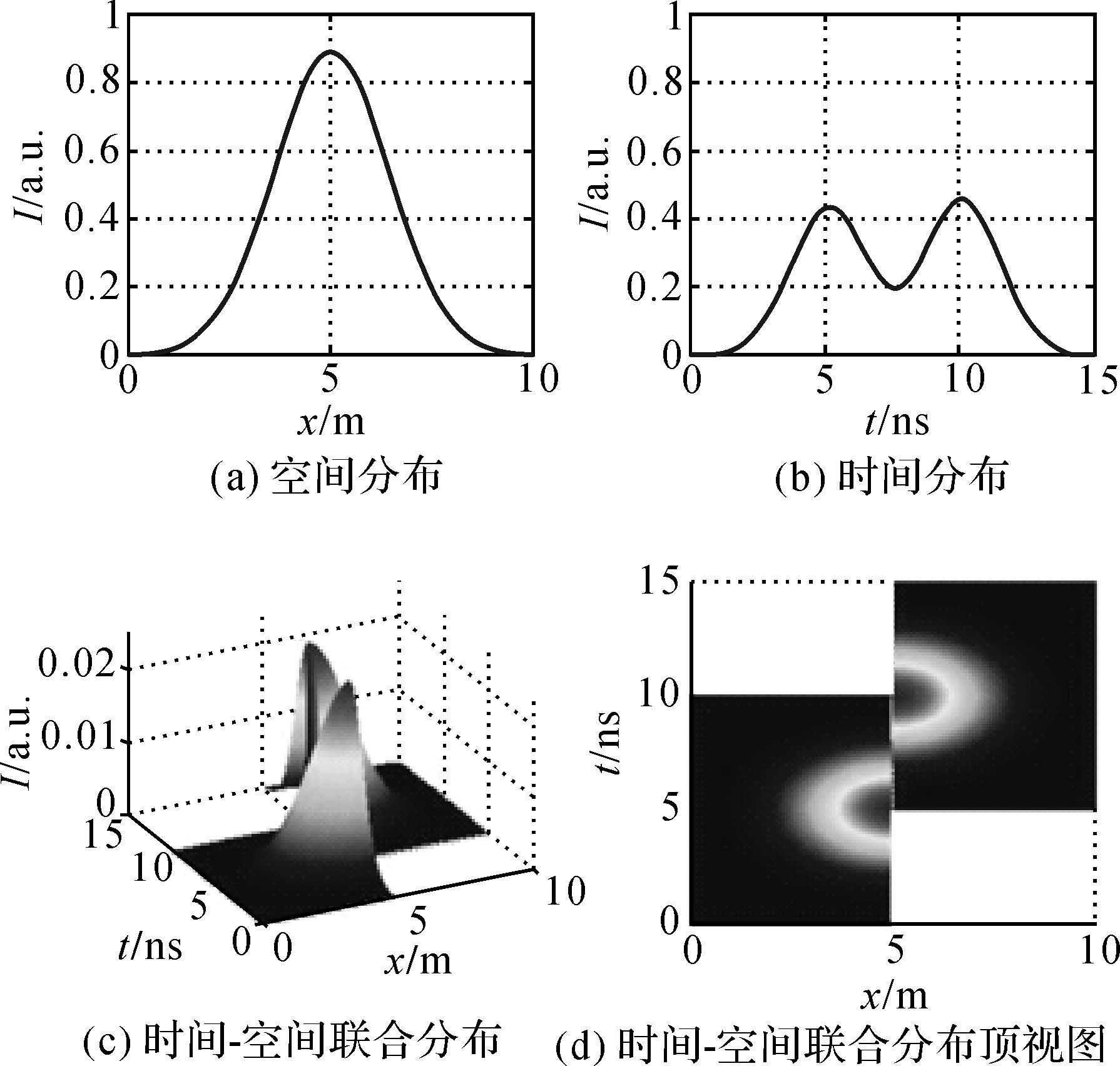
定义台阶顶和台阶底的平均值为台阶地形的高度真实值,即h1/2。台阶地形下,激光脉冲回波的时间、空间分布如图 8所示。回波信号的空间分布依旧不受地形影响,但时间分布曲线中间出现一个凹陷,这是由于台阶的顶和底分别给予了入射的激光脉冲不同的固定延时。
|
| 图 8 台阶地形回波信号的时间、空间分布特性 Fig. 8 Temporal and spatial distribution of echo pulse from stepped terrain |
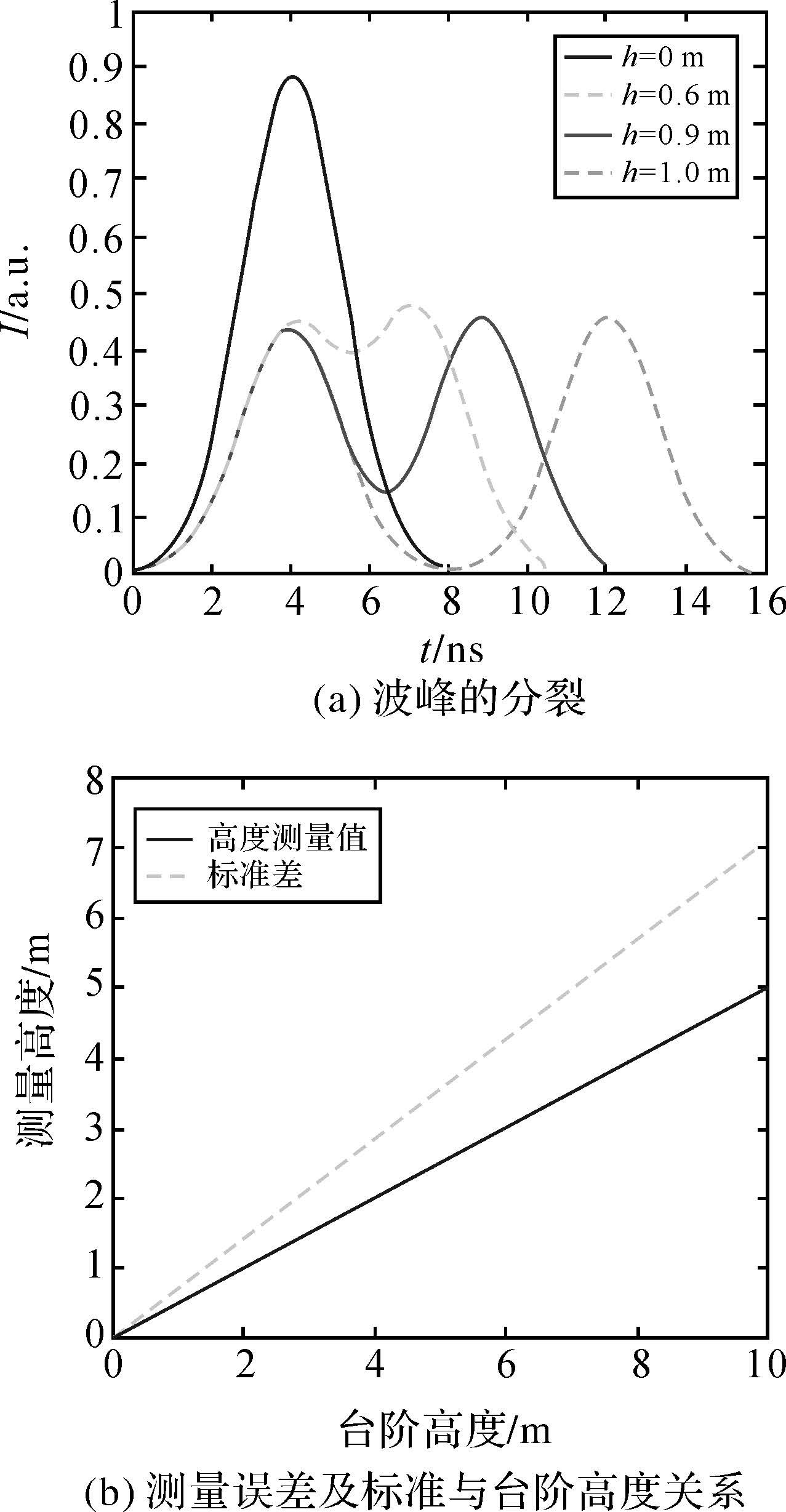
图 9给出了台阶地形对回波信号及探测精度的影响。从图 9(a)可以看出,随着台阶高度的增加,回波波形中间凹陷逐渐加大,直至分裂成两个高斯脉冲波形。图 9(b)给出了测量值、标准差与台阶高度的关系,可以看到,高度测量值与台阶高度成线性正比关系,且比例系数为1/2,是对台阶真实值的无偏测量。
|
| 图 9 台阶回波信号波形及测量精度与台阶高度的关系 Fig. 9 Relationship between echo pulse,detection precision and height of the step |
形成这种现象的原因是由于回波信号的两个波形相对于中间点成对称分布,因此在大量重复情况下,探测值在平均后趋于台阶高度的一半,即趋于真实高度值。随着台阶高度的增加,波峰间距增大,测量的标准差也逐渐增大。
3.3 植被地貌——反射率“斜坡”植被地貌情况下,由于物种的类型和稀疏程度不同,反射率呈现特定的分布,这里抽象为反射率的“斜坡”模型
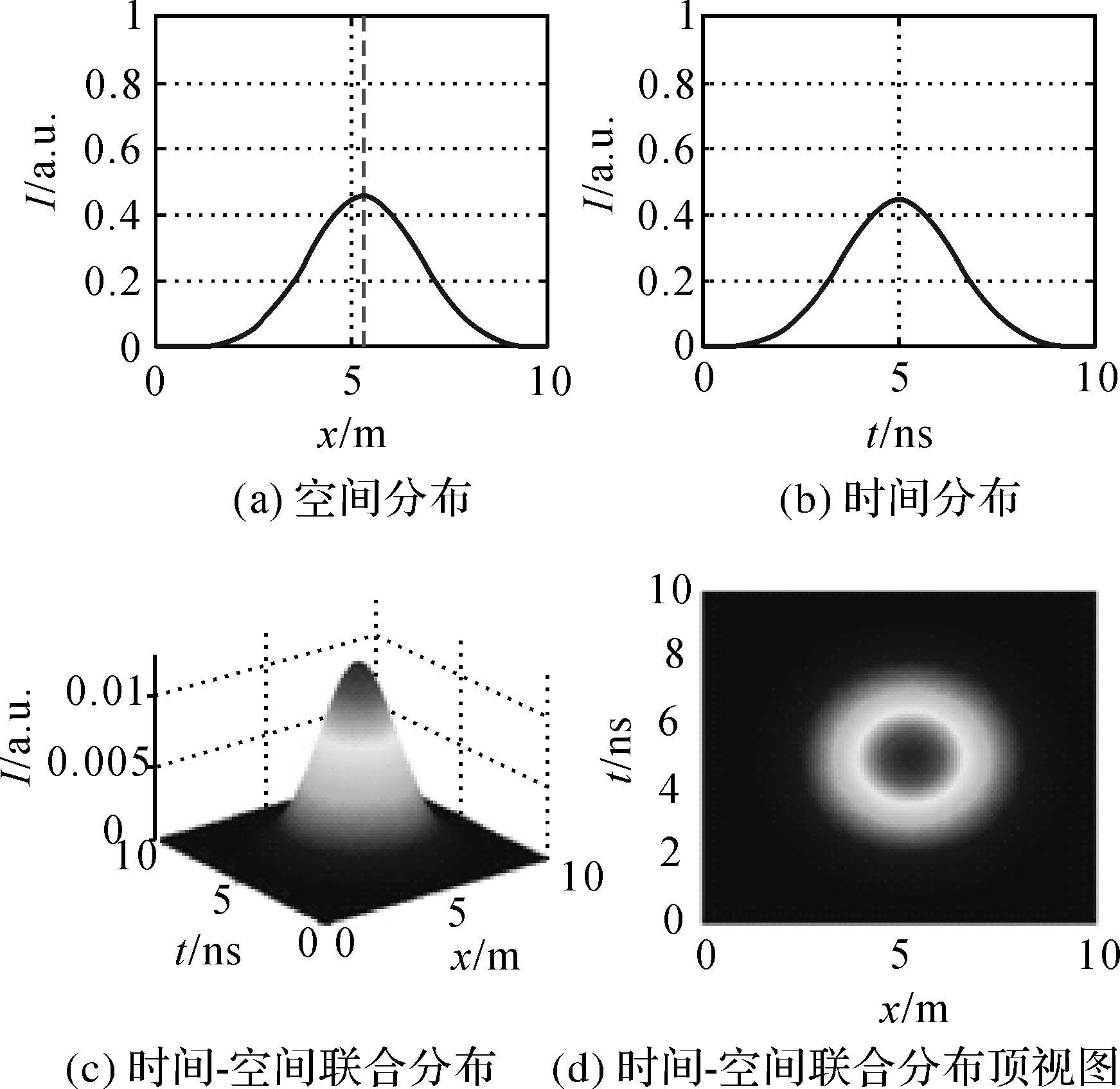
反射率“斜坡”地貌下,激光脉冲回波的时间、空间分布如图 10所示。
|
| 图 10 植被地貌回波信号的时间、空间分布特性 Fig. 10 Temporal and spatial distribution of echo pulse from vegetation terrain |
从图 10可以看出,由于地表反射率呈“斜坡”分布,回波信号中心向反射率大的方向偏移,但不影响信号的时间分布,因此高程测量误差来源于回波光子地面分布点的偏移。假设地面探测点偏移量为100 m,卫星轨道高度为400 km,则造成的高程测量误差为
误差在可以忽略范围内。实际上,地面反射率的不均匀分布造成激光光斑中心的偏移量很小,且在足印范围内,而激光三维测绘卫星的足印不大于10 m,因此植被地貌造成的高程测量误差可以忽略不计。
3.4 分界地貌——反射率“台阶”在水域与陆地、植被与沙地等分界面上,反射率会出现“台阶”式的跳跃,用以下模型表示
反射率“台阶”地貌下,激光脉冲回波的时间、空间分布如图 11所示。

|
| 图 11 分界地貌回波信号的时间、空间分布特性 Fig. 11 Temporal and spatial distribution of echo pulse from dividing terrain |
从图 11可以看出,分界地貌不影响回波信号的时间分布,但由于反射率的“台阶”式分布,回波信号在分界线的两边强度会有不均等的衰减,结果同样是回波信号强度重心的空间偏移。根据3.3小节的分析可知,该偏移造成的高程测量误差很小,可以忽略不计。
3.5 仿真试验采用Matlab建立模拟的DEM数据模型,如图 12(a)所示。仿真DEM数据面积为500 m×500 m,网格大小为1 m×1 m,包括斜坡、台阶地形和分界、植被地貌,其中,斜坡、台阶处地表反射率取0.3,植被地貌反射率呈正弦函数变化,在DEM图上以正弦起伏表示。

|
| 图 12 激光三维测绘仿真试验 Fig. 12 Simulation experiment of 3D LiDAR surveying |
激光三维测绘取网格分辨率为4 m×4 m。图 12中(b)、(c)、(d)分别为采用激光雷达探测1次、3次、8次时的结果,对应的测量误差平均值分别为:0.5 m、0.3 m、0.05 m。可以看出,在斜坡、台阶地形处,激光雷达的探测效果与原DEM数据很好地吻合,数据有一定随机误差,随着探测次数的累积误差逐渐减小;在分界、植被地貌处,探测结果也与原DEM数据具有良好的一致性。
4 结 论本文建立了不同地形、表貌物理模型,分析了不同地表空间起伏、反射率分布情况下的激光回波特性,并采用蒙特卡罗方法研究了不同地表形貌对Geiger探测模式的激光三维测绘卫星测量精度的影响,通过仿真试验验证,得到如下结论:
(1) 不同地形对回波脉冲的影响主要体现在脉冲的时间分布上,表现为回波信号的展宽、分裂等,但大量重复得到的测量平均值是平均高度值的无偏测量;随着地表坡度的增大、台阶高度的增大,测量标准差均增大。
(2) 不同地貌对回波信号的影响主要体现在脉冲的空间分布上,表现为回波信号强度中心的偏移,但偏移量较小,且造成的测量误差很小,可以忽略不计。
研究结果表明:激光三维测绘卫星对垂直陡变地形(如城市建筑)、斜坡地形(如山坡)、分界地貌(如水陆分界)和折射率起伏地貌(如植被地表等)具有良好的探测能力。
| [1] | KRIEGER G,MOREIRA A,FIEDLER H,et al. TanDEM-X:A Satellite Formation for High-resolution SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing,2007,45(11): 3317-3341. |
| [2] | ZHANG Guo, LI Fangting, JIANG Wanshou, et al. Study of Three-dimensional Geometric Model and Orientation Algorithms for Systemic Geometric Correction Product of Push-broom Optical Satellite Image[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 34-38. (张过, 厉芳婷, 江万寿, 等. 推扫式光学卫星影像系统几何校正产品的3维几何模型及定向算法研究[J]. )测绘学报, 2010, 39(1): 34-38. |
| [3] | HE Zhihua, HE Feng, HUANG Haifeng, et al. Influence of Distributed SAR Phase Synchronization Error on InSAR Performance and Experiment Validation[J]. Journal of Astronautics, 2012, 33(3): 353-357. (何志华, 何峰, 黄海风, 等. 分布式SAR相位同步误差的影响分析与试验验证[J]. )宇航学报, 2012, 33(3): 353-357. |
| [4] | TANG Xinming, ZHANG Guo, ZHU Xiaoyong. Thriple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198. (唐新明, 张过, 祝小勇. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. )测绘学报, 2012, 41(2): 191-198. |
| [5] | LEE K J, PARK Y, BUNKIN A, et al. Helicopter-based LiDAR System for Monitoring the Upper Ocean and Terrain Surface[J]. Applied Optics, 2002, 41(3): 401-406. |
| [6] | BUNKIN A F, DAVYDOV M A, REZOV A V, et al. Helicopter-based LiDAR Complex for Emission and Fluorescence Remote-sensing of Terrain Surfaces[J]. Laser Physics, 1994, 4(6): 1198-1201. |
| [7] | PHILBRICK C R. Overview of Raman LiDAR Techniques for Air Pollution Measurements[C]//LiDAR Remote Sensing for Industry and Environment Monitoring II, 2001.San Diego: SPIE, 2002: 136-150. |
| [8] | FOUCHE D G. Detection and False-alarm Probabilities for Laser Radars that Use Geiger-mode Detectors[J]. Applied Optics, 2003, 42(27): 5388-5398. |
| [9] | HENRIKSSON M. Detection Probabilities for Photon-counting Avalanche Photodiodes Applied to a Laser Radar System[J]. Applied Optics, 2005, 44(24): 5140-5147. |
| [10] | MARINO R M, DAVIS W R, RICH G C, et al. High-resolution 3D Imaging Laser Radar Flight Test Experiments[C]//Defense and Security. International Society for Optics and Photonics, 2005: 138-151. |
| [11] | ZWALLY H J, SCHUTZ R, ABDALATI W, et al. ICESat’s Laser Measurements of Polarice, Atmosphere, Ocean, and Land[J]. Journal of Geodynamics,2002, 34(4): 405-445. |
| [12] | ABSHIRE J B , SUN X L , ROBERT S A. Mars Orbiter Laser Altimeter:Receiver Model and Performance Analysis[J]. Applied Optics, 2000, 39(15): 2449-2460. |
| [13] | CHEN Junyong, ZHANG Chuanyin, DANG Yamin. Lunar Spatial Exploration, Surveying and Mapping[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 189-195. (陈俊勇, 章传银, 党亚民. 月球航天探测和月球测绘[J]. )测绘学报, 2005, 34(3): 189-195. |
| [14] | HU Y H, SHU X Y, XUE Y Q. Experiment Study of Laser Echo Identities of Terrain Object[J]. Infrared and Laser Engineering, 2002, 32(2): 105-108. |
| [15] | ALBOTA M A, AULL B F, FOUCHE D G, et al. Three-dimensional Imaging Laser Radars with Geiger-mode Avalanche Photodiode Arrays[J]. Lincoln Laboratory Journal, 2002, 13(2): 351-370. |
| [16] | YU Qiuze, CAO Ju, TAN Yihua, et al. Simulation of Intensity Image of Airborne-based Imaging Laser Radar Based on DEM and Visible Image[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 249-253. (于秋则, 曹矩, 谭毅华, 等. 基于DEM与可见光图像的机载激光成像雷达强度像仿真[J]. )测绘学报, 2004, 33(3): 249-253. |
| [17] | O′ BRIEN M E, FOUCHE D G. Simulation of 3D Laser Rader Systems[J]. Lincoln Laboratory Journal, 2005, 15(1): 37-60. |
| [18] | ZHOU Shihong, TONG Qingwei, LI Xin, et al. Research on Performance of Three-dimensional Laser Imaging System Based on Multi-pulse Detection Mode[J]. Bulletin of Surveying and Mapping, 2014(S0): 1-3. (周世宏, 童庆为, 李鑫, 等. 基于多脉冲探测模式的激光三维成像性能研究[J]. )测绘通报, 2014(S0): 1-3. |
| [19] | GARDNER C S. Target Signatures for Laser Altimeters: an Analysis[J]. Applied Optics, 1982, 21(3): 448-453. |
| [20] | MCADOO D C, FARRELL S L, LAXON S W, et al. Arctic Ocean Gravity Field Derived from ICESat and ERS-2 Altimetry: Tectonic Implications[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2008, 113(B5). |
| [21] | AULL B F, LOOMIS A H, YOUNG D J, et al. Geiger Mode Avalanche Photodiodes for Three-dimensional Imaging[J]. Lincoln Laboratory Journal, 2002, 13(2): 335-349. |
| [22] | MARINO R M, STEPHENS T, HATCH R E, et al. A Compact 3D Imaging Laser Radar System Using Geiger-mode APD Arrays: System and Measurements[C] //Aero Sense 2003. International Society for Optics and Photonics, 2003: 1-15. |
| [23] | XU Lu, ZHANG Yu, ZHANG Yong, et al. Research on the Detection Performance of Geiger-mode APD[J]. Chinese Journal of Lasers. 2012, 39(4): 206-211. (徐璐, 张宇, 张勇, 等. 盖革模式雪崩光电二极管激光雷达累积探测性能的研究[J]. )中国激光, 2012, 39(4): 206-211. |
| [24] | WANG Fei. Researches on Performance and Range Accuracy of Laser Imaging System Based on Geiger Mode Detectors[D]. Harbin: Harbin Institute of Technology, 2010. (王飞. 基于Geiger探测器的激光成像性能及测距精度研究[D]. )哈尔滨: 哈尔滨工业大学, 2010. |