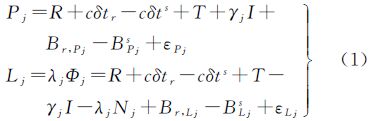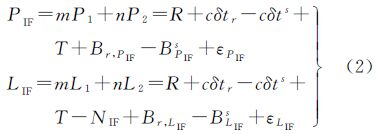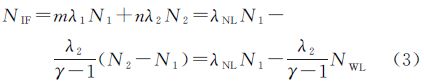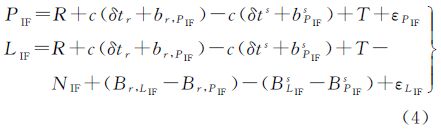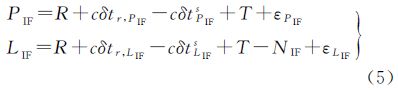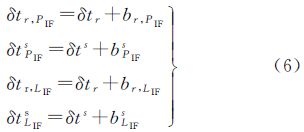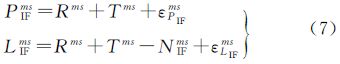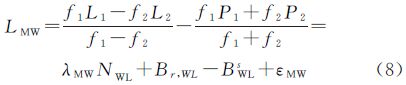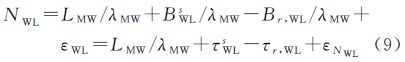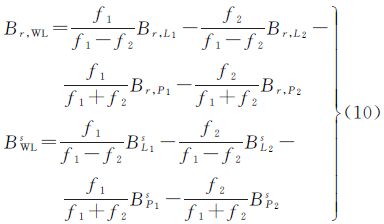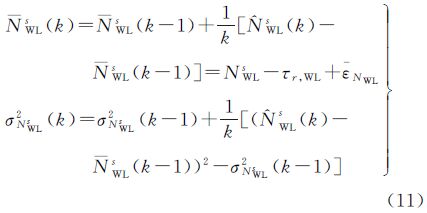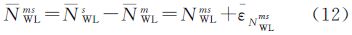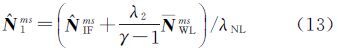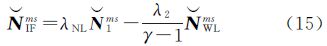1 引 言
精密单点定位(precise point positioning,PPP)技术摆脱了基准站的限制,在航空摄影测量、海洋测量等高精度测量领域有着广泛的应用前景。模糊度浮点解的动态PPP仅能达到分米级到厘米级的定位精度,与厘米级定位精度的相对定位还存在差距。近几年发展起来的PPP模糊度固定技术被证实可以有效提高收敛速度、改善定位精度,吸引了国内外学者和研究机构的广泛关注。目前,常用的PPP模糊度固定方法有3种:文献[1]提出的星间单差法、文献[2, 3]提出的整数相位钟法以及文献[4]提出的钟差解耦法。文献[5]分析了星间单差法与整数相位钟法的区别;文献[6, 7, 8]从不同角度分别独立证明了这3种方法在数学模型上的等价性,但在所用产品和算法实现上还有差异。文献[9, 10, 11]对星间单差法PPP模糊度固定进行了深入研究,但对整数相位钟法研究较少。尽管有3种PPP模糊度固定方法可供用户选择,但目前仅CNES公布了用于整数相位钟法PPP模糊度固定的产品,而另外两种方法还未有公开的常规产品供用户使用。文献[12]给出了CNES所发布产品的服务器端算法,但对用户如何使用该产品进行PPP模糊度固定未有详细论述。文献[2, 3]给出的整数相位钟法PPP模糊固定策略中缺少必要的质量控制,这将直接影响固定效果。因此研究基于整数相位钟法的用户端PPP模糊度固定模型和顾及质量控制的模糊度固定策略很有必要。
本文首先推导了基于整数相位钟法进行PPP模糊度固定的函数模型;与文献[2, 3]提出的先固定非差宽巷模糊度然后直接估计并固定非差窄巷模糊度不同,本文提出一种顾及质量控制的逐级模糊度固定策略;最后通过大量动态PPP算例对本文模型和所提模糊度固定策略进行验证分析。
2 模糊度固定模型浮点解与固定解PPP数学模型的差异主要在函数模型,本文在文献[7, 8]推导的整数相位钟法PPP模糊度固定模型的基础上进行了重新梳理。对于原始的伪距和载波相位观测方程可以表示为
式中,下标r和上标s分别指接收机和卫星;下标j表示载波频率,对于GPS而言,j取1或2;P表示伪距观测值(m);L表示载波相位观测值(m);R表示站星间几何距离(m);c表示光速(m/s);δtr和δts分别表示接收机钟差和卫星钟差(s);T表示对流层延迟(m);γj=f12/fj2,其中fj表示载波频率(Hz);I表示f1频率上的电离层延迟项(m);λj表示波长(m);Φj表示以周为单位的载波相位观测值;Nj表示初始整周模糊度(周);Br,Pj和BPjs分别表示伪距观测值的接收机端和卫星端偏差(m);Br,Lj和BLjs分别表示载波相位观测值的接收机端和卫星端偏差(m);ε表示观测噪声(m)。本文假定已经进行了天线相位中心、潮汐、相位缠绕等改正,因此未在观测方程中列出这些项。由式(1)可以得到伪距和载波相位的消电离层组合观测方程
式中,PIF和LIF分别表示伪距和载波相位的消电离层组合观测值(m);m、n表示消电离层组合系数;Br,PIF、BPIFs、Br,LIF和BLIFs表示相应的消电离层组合偏差(m);NIF表示以m为单位的消电离层模糊度,它可以分解为N1和宽巷模糊度NWL组合的形式 式中,λNL表示窄巷波长,约为10.7cm。由于N1是以窄巷波长为系数,通常称N1为窄巷模糊度。在式(2)的基础上稍加变形可得到传统的模糊度浮点解PPP模型的观测方程
式中,b表示偏差项B对应的时间延迟项(s),即b=B/c。在传统模型中,将IGS发布的伪距卫星钟差产品δts+bPIFs应用到载波相位观测值上,同时估计伪距接收机钟差δtr + br,PIF,这将导致所估计的消电离层模糊度参数NIF受(Br,LIF-Br,PIF)-(BLIFs-BPIFs) 项的污染,所估计消电离层模糊度无法准确分解成如式(3)所示的宽巷和窄巷模糊度的组合形式,这就是传统模型无法将消电离层模糊度进行固定的原因。整数相位钟法PPP模糊度固定的重要思想是将伪距钟差和载波相位钟差进行区分,使得所估计的消电离层模糊度不再受到污染,在式(2)的基础上稍加变形可得到
式中,δtr,PIF和δtPIFs分别表示伪距的接收机钟差和卫星钟差(s);δtr,LIF和δtLIFs分别表示载波相位的接收机钟差和卫星钟差(s)。它们的具体形式为 服务器端须同时估计以上4种不同的钟差,从而确保消电离层模糊度NIF能准确按照式(3)进行分解。因此,当用户将CNES发布的精密卫星钟差产品用于载波相位消电离层组合观测值LIF、将IGS发布的精密卫星钟差产品用于伪距消电离层组合观测值PIF并同时估计两类不同的接收机钟差时,就能得到具备按式(3)准确分解特性的消电离层模糊度,从而能够实现模糊度固定。对于用户端而言,为避免同时估计两类接收机钟差,可对式(5)进行卫星间求差,并认为已经进行了卫星钟差项的改正,可得
式(7)即为整数相位钟法PPP模型的观测方程,式中消掉了接收机钟差项,上标ms表示由非基准星s的某一量减去基准星m对应的量构成的单差量,式(7)中待求的参数有位置参数、对流层参数和单差消电离层模糊度参数。在实际的用户端算法中,先得到单差消电离层模糊度的浮点解和单差宽巷模糊度的固定解,此时利用式(3)可得到单差窄巷模糊度的浮点解及其方差协方差阵,然后通过适当的模糊度固定方法将单差窄巷模糊度进行固定,最后利用固定的单差宽巷模糊度和固定的单差窄巷模糊度求取单差消电离层模糊度的固定解,以此为约束求取位置等其他参数的固定解。以上就是逐级模糊度固定的基本思路,下一节会给出详细的步骤和质量控制策略。本文的模糊度固定方法与文献[2, 3]提出的方法虽有不同,但是数学模型上是一致的。除了确保模型一致外,用户端还要在误差改正模型以及数据处理策略上尽可能与服务器端算法保持一致。为了保证宽巷产品的连续性,δtLIFs不仅吸收了bLIFs,还会吸收部分宽巷延迟[12],须配合使用CNES发布的整数相位钟产品和宽巷模糊度偏差产品才能实现模糊度固定。
3 顾及质量控制的逐级模糊度固定策略 3.1 固定单差宽巷模糊度通常使用MW组合观测值来解算宽巷模糊度,MW组合观测值定义为载波相位观测值的宽巷组合减去伪距观测值的窄巷组合。由式(1)可得
式中,LMW即为MW组合观测值(m)。于是可得宽巷模糊度的求解公式为 式中,λMW表示宽巷波长,约为86cm;Br,WL和BWLs分别表示接收机端和卫星端的宽巷偏差(m);τr,WL和τWLs则是相应的以周为单位的宽巷偏差,其中Br,WL和BWLs的具体形式为若要按照式(9)求出宽巷模糊度NWL,需要去除宽巷周偏差τr,WL和τWLs的影响,其中卫星端宽巷周偏差τWLs已经作为产品提供给用户,文中对平滑后的宽巷模糊度进行星间作差来消除接收机端宽巷周偏差τr,WL的影响。由于受伪距观测噪声的影响,还须对式(9)进行多历元平滑(取平均)来降低伪距观测噪声的影响,对单颗卫星平滑公式如下[13]
式中,NWLs表示宽巷模糊度的平滑值;k和k-1分别表示当前和前一个观测历元;σNWLs表示宽巷模糊度的平滑标准差。当同时平滑两颗卫星时,对平滑的宽巷模糊度求差得可以使用文献[14]提出来的固定准则或是文献[15]提出来的纳伪概率可控的四舍五入法来决定是否对NWLms就近取整得到单差宽巷模糊度的整数解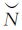 WLms。由于宽巷波长较长,因此较容易固定。
WLms。由于宽巷波长较长,因此较容易固定。
假设已经求得了精度较好的单差消电离层模糊度估值向量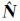 IFms和固定的单差宽巷模糊度向量
IFms和固定的单差宽巷模糊度向量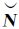 WLms,将它们代入式(3)得到单差窄巷模糊度浮点解向量
WLms,将它们代入式(3)得到单差窄巷模糊度浮点解向量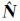 1ms
1ms
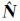 1ms的方差协方差阵近似为
1ms的方差协方差阵近似为
以单差窄巷模糊度的浮点解向量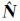 1ms及其方差协方差阵
1ms及其方差协方差阵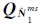 作为LAMBDA(least-square ambiguity decorrelation adjustment)算法的输入量进行整周模糊度解算,综合使用ratio值和模糊度解算成功率作为固定接受准则[16, 17, 18]。由于窄巷波长较短,因此较难固定,这一步也成为PPP模糊度固定的关键。为了避免错误固定的单差宽巷模糊度以及个别卫星消电离层模糊度收敛不完全、精度较差导致模糊度检核失败等情况,本文使用文献[19]提出的部分模糊度解算方法,即构造所有可能的卫星组合,对每一个组合进行整周模糊度解算,从中找到满足固定接受准则的组合。
作为LAMBDA(least-square ambiguity decorrelation adjustment)算法的输入量进行整周模糊度解算,综合使用ratio值和模糊度解算成功率作为固定接受准则[16, 17, 18]。由于窄巷波长较短,因此较难固定,这一步也成为PPP模糊度固定的关键。为了避免错误固定的单差宽巷模糊度以及个别卫星消电离层模糊度收敛不完全、精度较差导致模糊度检核失败等情况,本文使用文献[19]提出的部分模糊度解算方法,即构造所有可能的卫星组合,对每一个组合进行整周模糊度解算,从中找到满足固定接受准则的组合。
受模型强度弱以及滤波收敛不完全的影响,即便通过了单差窄巷模糊度的固定准则仍可能出现错误固定。文献[20]的实际算例表明即便窄巷模糊度都很接近整数且通过了ratio检验,使用LAMBDA算法仍有可能得到错误的固定结果。文献[12]研究发现当浮点解PPP的位置精度小于5cm时才能保证可靠的窄巷模糊度固定。综合以上考虑,本文判断PPP扩展卡尔曼滤波器满足给定收敛条件时才开始进行单差窄巷模糊度固定,即从PPP扩展卡尔曼滤波器输出的待估参数方差协方差阵中提取3个位置参数的方差项,以三维位置方差的平方根是否小于5cm作为收敛条件;必要时可设置连续多个历元单差窄巷模糊度固定成功且前后历元同一卫星固定的结果一致时才去固定单差消电离层模糊度
当固定了单差消电离层模糊度后,以此为约束求取位置等其他参数的固定解。
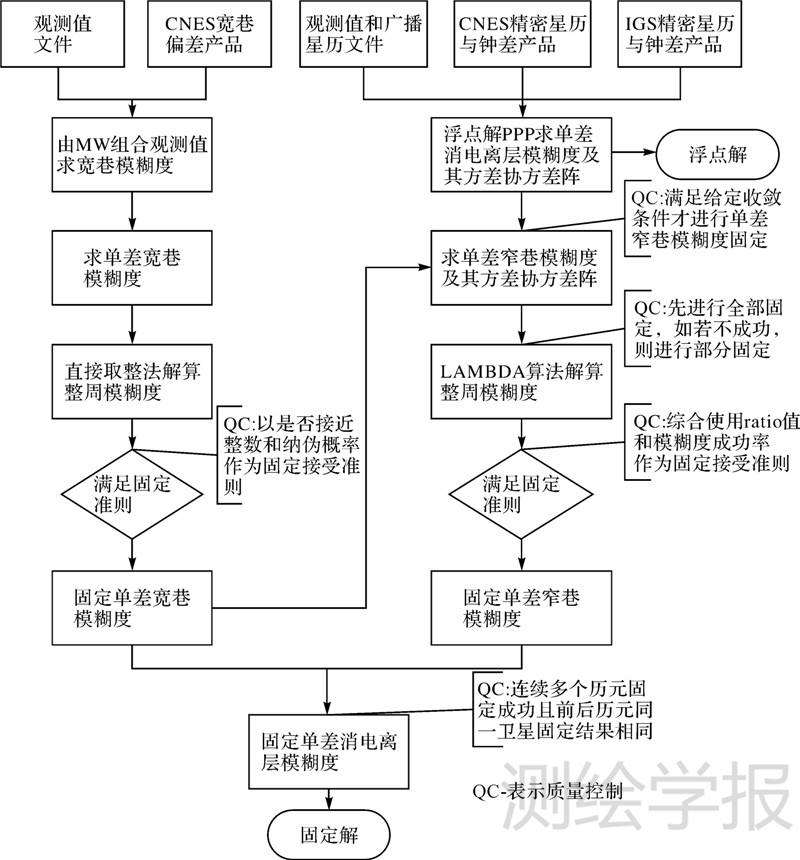
图 1给出了实施顾及质量控制的逐级模糊度固定策略的流程图:先进行PPP解算得到单差消电离层模糊度浮点解及其方差协方差阵;再利用MW组合观测值[13]求取单差宽巷模糊度的浮点解并进行宽巷偏差改正,以是否接近整数和纳伪概率作为固定准则[14]求其固定解;当满足给定收敛条件时再利用式(13)和式(14)得到单差窄巷模糊度的浮点解及其方差协方差阵,使用LAMBDA算法[16]并结合部分模糊度固定算法[19]来求单差窄巷模糊度固定解,并以ratio值和模糊度成功率作为固定准则[17, 18];当连续多个历元固定成功且前后历元固定相同时,再利用固定的单差宽巷模糊度和固定的单差窄巷模糊度求取单差消电离层模糊度的固定解,以此为约束求取其他参数的固定解。
|
| 图 1 顾及质量控制的逐级模糊度固定策略 Fig. 1 Cascaded ambiguity fixing strategy with special regard to quality control |
选取2013年12月14日10个IGS站(ALGO、ANKR、BJFS、DUBO、FLIN、GOPE、HLFX、MDVJ、UNB3、YAR3)的观测数据,采样间隔为30s,基于本文模型和顾及质量控制的逐级模糊度固定策略研制了软件PPNav并以此进行解算试验。将该天2∶00至22∶00的GPS观测数据分割成每4h为1个观测时段,这样每个测站可划分5个观测时段,10个IGS测站共有50个观测时段。对每个观测时段进行浮点解和固定解PPP这两种模式的静态模拟动态解算试验。PPP扩展卡尔曼滤波器中所使用的误差改正模型与CNES使用的模型保持一致,高度角设置为10°,位置参数建模成白噪声过程,天顶方向对流层延迟建模成随机游走,模糊度参数建模成常数。将解算结果与IGS坐标进行比较,得到每个测站浮点解与固定解PPP位置误差。
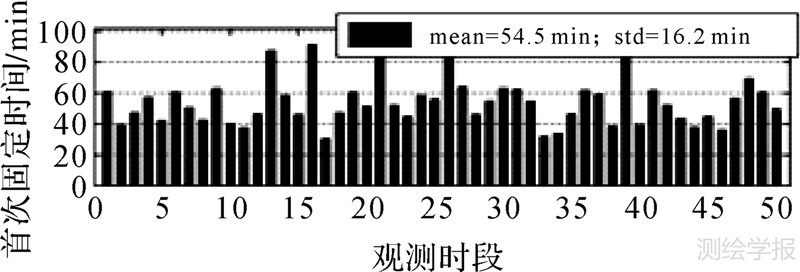
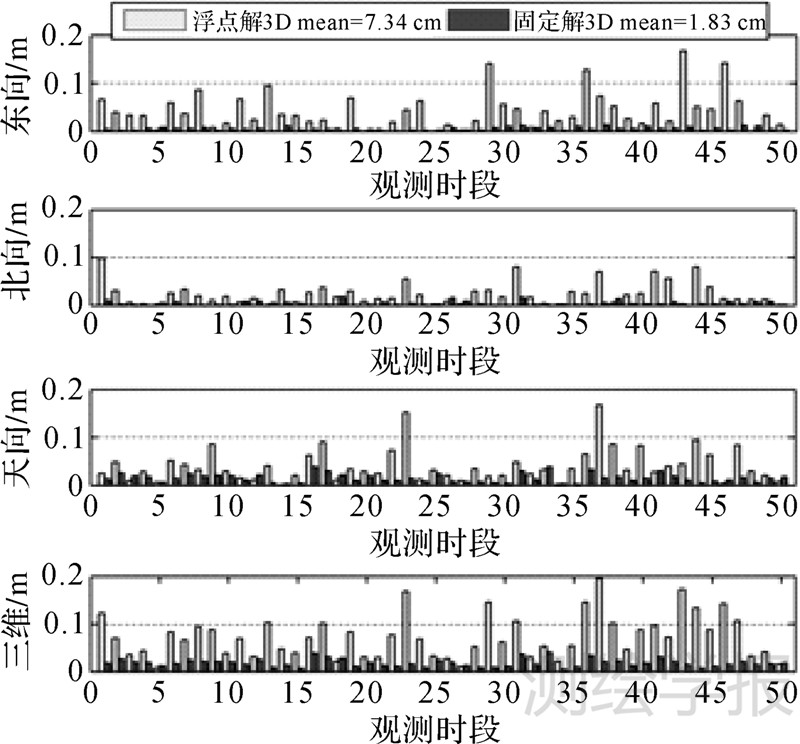
图 2统计了这50个观测时段的首次固定时间(time to first fixed solution,TFFS),首次固定时间对应的历元称为首次固定历元。图 3比较了50个观测时段首次固定历元处的浮点解和固定解PPP位置误差绝对值。表 1为具体的统计结果。对这50个观测时段的首次固定统计结果分析可知,平均54.5min就可实现首次固定,一旦实现固定,PPP的三维位置误差的平均值由7.34cm迅速下降到1.83cm,这表明固定解PPP具有更快的收敛速度。
|
| 图 2 50个观测时段的首次固定时间 Fig. 2 TFFS of 50 sessions |
|
| 图 3 50个观测时段首次固定历元处浮点解与固定解PPP位置误差 Fig. 3 Float and fixed PPP positioning error of first fixed solution for 50 sessions |
| 东向/m | 北向/m | 天向/m | 三维/m | ||
| 浮点解 | 平均值 | 0.0431 | 0.0246 | 0.0418 | 0.0734 |
| PPP | 标准差 | 0.0385 | 0.0231 | 0.0350 | 0.0451 |
| 固定解 | 平均值 | 0.0050 | 0.0047 | 0.0156 | 0.0183 |
| PPP | 标准差 | 0.0034 | 0.0045 | 0.0092 | 0.0084 |
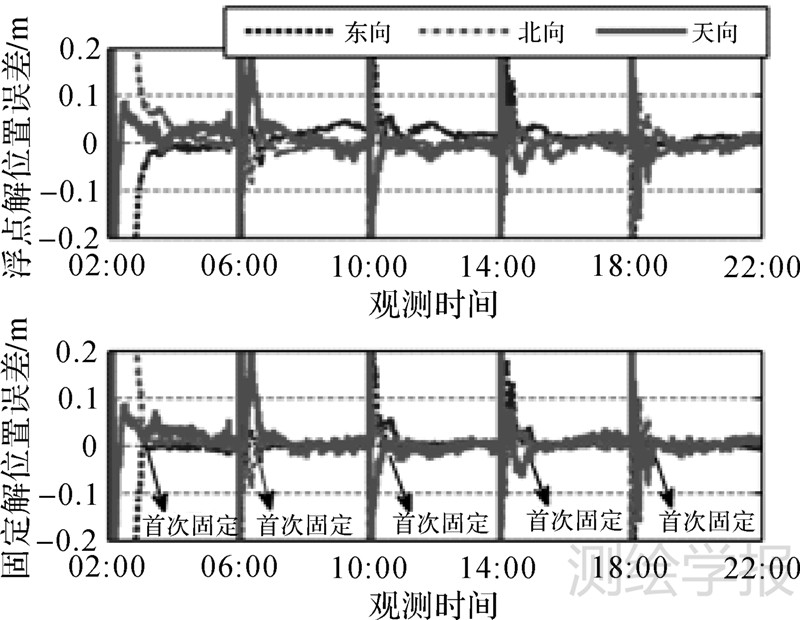
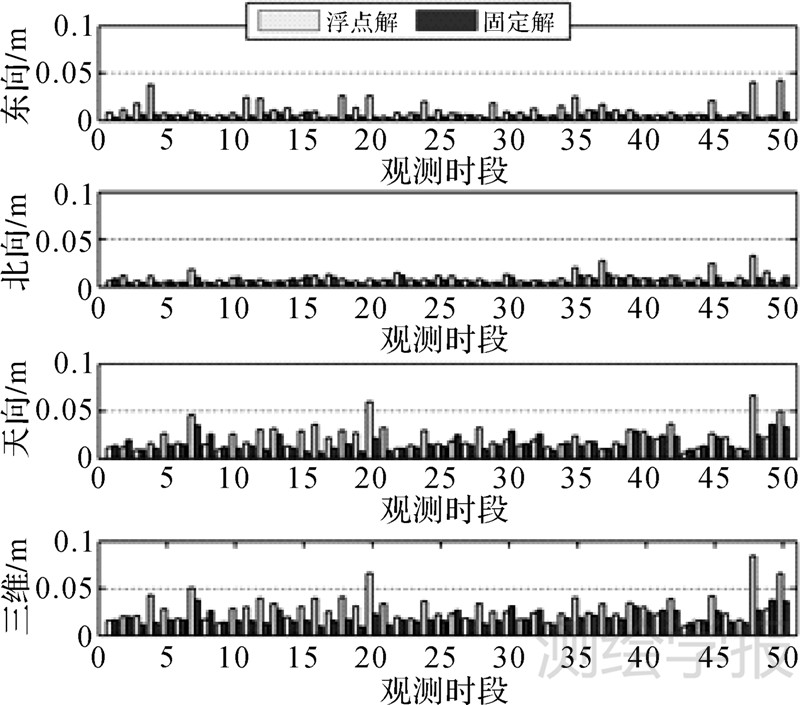
限于篇幅,仅给出ALGO站5个观测时段的浮点解和固定解PPP的位置误差图,如图 4所示。对图 4中首次固定后的位置误差分析可知,固定解PPP的精度和稳定性都要优于浮点解PPP。图 5统计了50个观测时段最后1h的位置误差的均方根(root mean square,RMS),之所以统计最后1h,是因为最后1h浮点解PPP已经完全收敛,此时的精度统计与比较更有意义。表 2进一步统计了图 5中50组位置误差RMS的平均值和标准差。综合图 5和表 2可以发现,固定解PPP的位置精度优于浮点解PPP,且固定解PPP的精度结果更为稳定。
|
| 图 4 ALGO站浮点解和固定解PPP位置误差 Fig. 4 Float and fixed PPP positioning error of ALGO station |
|
| 图 5 50个观测时段最后1h浮点解和固定解PPP位置误差RMS Fig. 5 RMS positioning error of float and fixed PPP for the last 1h of 50 sessions |
| 东向/m | 北向/m | 天向/m | 三维/m | ||
| 浮点解 | 平均值 | 0.0127 | 0.0099 | 0.0230 | 0.0294 |
| PPP | 标准差 | 0.0094 | 0.0059 | 0.0127 | 0.0143 |
| 固定解 | 平均值 | 0.0054 | 0.0072 | 0.0164 | 0.0192 |
| PPP | 标准差 | 0.0016 | 0.0025 | 0.0078 | 0.0072 |
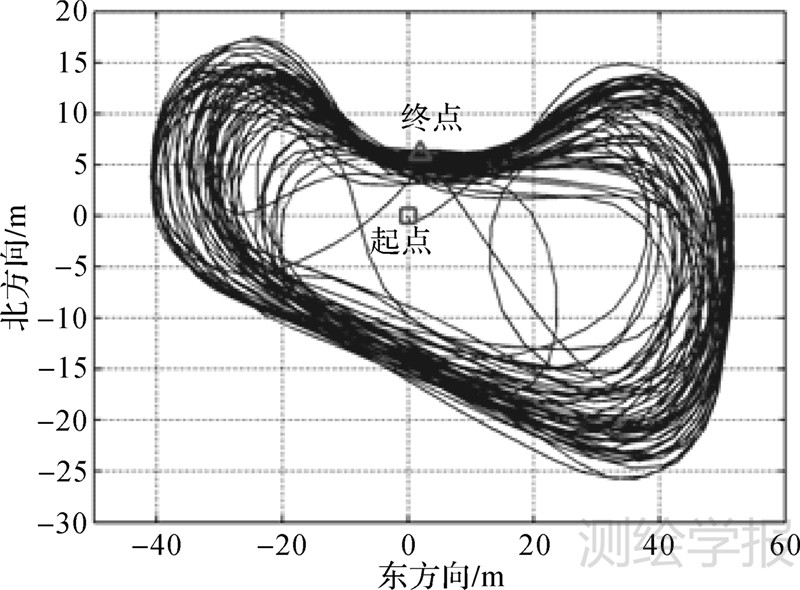
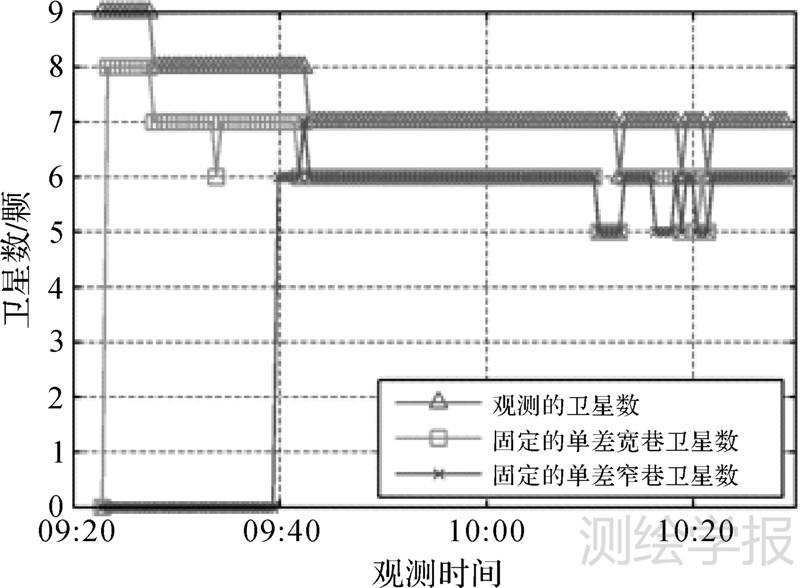
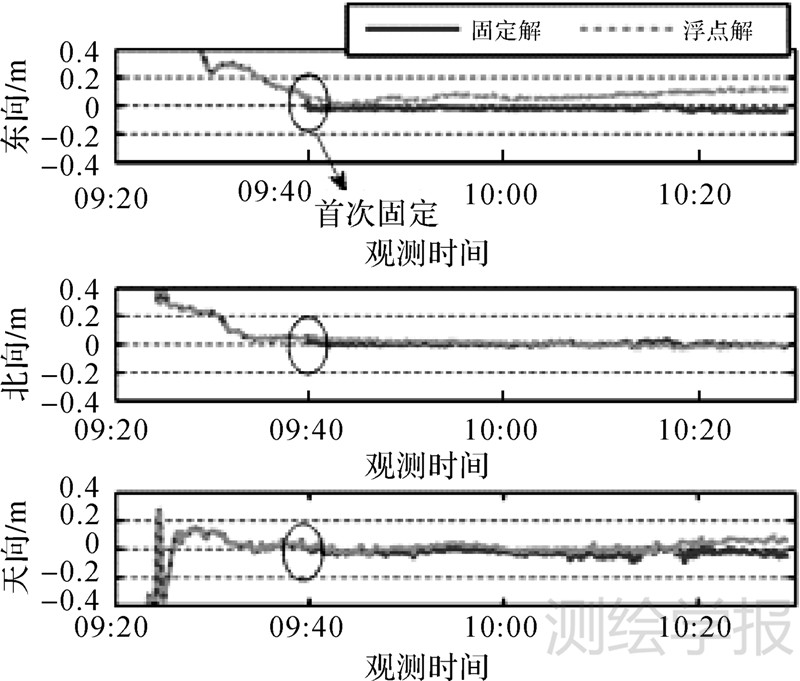
选取2013年11月14日的车载数据进行解算试验。测试地点为武汉某空旷广场,同时架设有基准站,测试时长近4000s,采样间隔为1s,测试轨迹如图 6所示。所用接收机为NovAtel OEM4双系统接收机,但只处理GPS观测数据。使用Bernese软件对基准站观测数据进行解算得到基准站高精度坐标;使用商用GNSS数据后处理软件GrafNav对基准站和流动站数据进行相对定位解算得到流动站的高精度定位结果并作为参考值。对该组跑车数据使用自研软件PPNav进行两种模式的解算,解算设置与4.1节一致。解算中观测到的总卫星数、固定的单差宽巷、窄巷卫星数如图 7所示。将浮点解、固定解PPP位置结果与相对定位结果比较,得到每个历元的位置误差,如图 8所示。对最后30min的位置误差进行统计得到浮点解和固定解的位置误差RMS,如表 3所示。从图 8和表 3中可以看出,固定解的精度比浮点解得到显著提升,特别是东方向。
|
| 图 6 测试车辆平面轨迹 Fig. 6 Horizontal routing of the test vehicle |
|
| 图 7 总的卫星数、固定的单差宽(窄)巷卫星数 Fig. 7 Total satellite number and fixed single-difference wide-lane/narrow-lane satellite number |
|
| 图 8 车辆试验浮点解和固定解PPP位置误差 Fig. 8 Float and fixed PPP positioning error of vehicle test |
| 位置误差的RMS值 | ||||
| 东向/m | 北向/m | 天向/m | 三维/m | |
| 浮点解PPP | 0.0878 | 0.0136 | 0.0378 | 0.0966 |
| 固定解PPP | 0.0229 | 0.0117 | 0.0330 | 0.0418 |
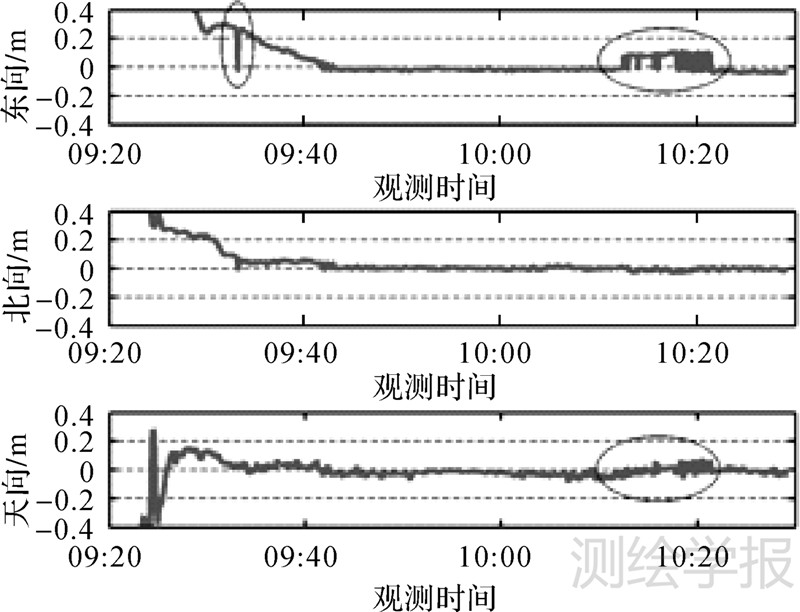
为了验证本文所提顾及质量控制的逐级模糊度固定策略的效果,不再进行收敛条件判别和部分模糊度固定,然后对该组车载试验数据进行固定解PPP解算。图 9为相应的位置误差图,其中在9:33出现若干历元能够成功固定,但是其可靠性得不到保证;比较显著的是在10:18附近历元,由于个别卫星观测条件差等因素的影响,使得当对所有单差窄巷模糊度进行固定时无法通过固定准则而造成无法成功固定。但当使用顾及质量控制的逐级模糊度固定策略时,由于策略中包含了部分模糊度固定,仍然可以通过部分模糊度固定得到10:18附近历元的准确固定解,也就是图 8所展示结果。对图 7中10:18附近的卫星数目分析也可以发现,存在固定的单差窄巷卫星数要比固定的单差宽巷卫星数少的情况,这说明此时已经进行了部分模糊度固定。
|
| 图 9 未进行收敛条件判别和部分模糊度固定的固定解PPP位置误差 Fig. 9 Fixed PPP positioning error of vehicle test without convergence decision and partial ambiguity fixing |
本文分析了整数相位钟法PPP模糊度固定的模型,提出了一种顾及质量控制的逐级模糊度固定策略。通过10个IGS站共50个观测时段的观测数据和实际的车载观测数据的动态解算试验对本文模型与所提模糊度固定策略进行了验证,大量算例表明:当浮点解PPP收敛到一定精度的时候,通过模糊度固定可直接达到厘米级的定位精度;固定解PPP有着更好的定位精度和稳定性。
精密单点定位模糊度得以正确固定依赖于浮点解模糊度收敛到一定精度,当GPS卫星数目不足或几何构形不好的时候,浮点解模糊度难以快速收敛到一定精度,这就会影响模糊度的固定。下一步需研究加入GLONASS卫星来辅助GPS的PPP模糊度固定。
致谢:感谢法国CNES的Loyer博士、澳大利亚科廷科技大学的张宝成博士、武汉大学的史俊波博士和李盼博士生对笔者的指点和帮助。
| [1] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. |
| [2] | LAURICHESSE D, MERCIER F. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007). [s.l.]: ION, 2001: 839-848. |
| [3] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135-149. |
| [4] | COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123-135. |
| [5] | ZHANG Baocheng, OU Jikun. On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 710-716. (张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40(6): 710-716.) |
| [6] | GENG J, MENG X, DODSON A H, et al. Integer Ambiguity Resolution in Precise Point Positioning: Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581. |
| [7] | SHI J. Precise Point Positioning Integer Ambiguity Resolution with Decoupled Clocks[D]. Calgary: University of Calgary, 2012. |
| [8] | SHI J, GAO Y. A Comparison of Three PPP Integer Ambiguity Resolution Methods [EB/OL]. 2013-10-01 [2014-02-01] http://link.springer.com/static-content/lookinside/391/art%253A10.1007%252Fs10291-013-0348-2/000.png. |
| [9] | ZHANG X, LI P, GUO F. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Advances in Space Research, 2013, 51(1): 153-161. |
| [10] | ZHANG X, LI P. Assessment of Correct Fixing Rate for Precise Point Positioning Ambiguity Resolution on a Global Scale[J]. Journal of Geodesy, 2013, 87(6): 579-589. |
| [11] | LI P, ZHANG X. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471. |
| [12] | LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012, 86(11): 991-1003. |
| [13] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202. |
| [14] | DONG D N, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1989, 94(B4): 3949-3966. |
| [15] | LI Bofeng, SHEN Yunzhong, ZHANG Xingfu. Error Probability Controllable Integer Rounding Method and Its Application to RTK Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 483-489. (李博峰, 沈云中, 张兴福. 纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用[J]. 测绘学报, 2012, 41(4): 483-489.) |
| [16] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |
| [17] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606-612. |
| [18] | LI T, WANG J, LAURICHESSE D. Modeling and Quality Control for Reliable Precise Point Positioning Integer Ambiguity Resolution with GNSS Modernization[J]. GPS Solutions, 2014, 18(3): 429-442. |
| [19] | PARKINS A. Increasing GNSS RTK Availability with a New Single-epoch Batch Partial Ambiguity Resolution Algorithm[J]. GPS Solutions, 2011, 15(4): 391-402. |
| [20] | JOKINEN A, FENG S, SCHUSTER W, et al. GLONASS Aided GPS Ambiguity Fixed Precise Point Positioning[J]. Journal of Navigation, 2013, 66(3): 399-416 |