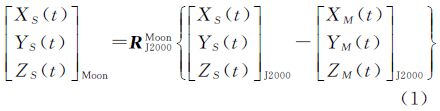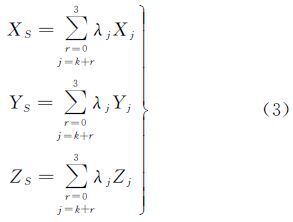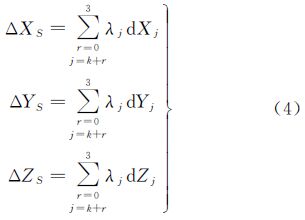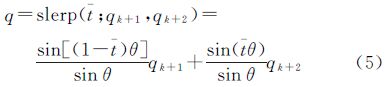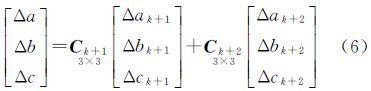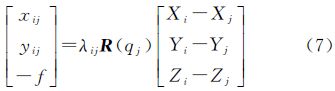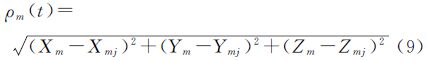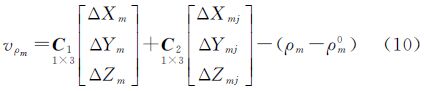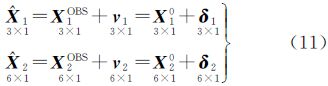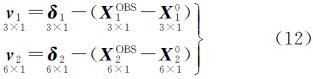2. 国家测绘地理信息局 第一航测遥感院,陕西 西安710054
2. The First Institute of Photogrammetry and Remote Sensing,National Administration of Surveying,Mapping and Geoinformation,Xi’an 710054,China
1 引 言
CE-1探月卫星轨道为200km圆形轨道[1]，携带三线阵立体相机和激光高度计两种主要制图载荷，其主要任务是获取月球表面的形貌信息。在卫星沿轨方向，激光高度计以1Hz的频率向月表发射激光脉冲，形成线性激光剖面，通过精确测定脉冲往返时间实时计算卫星到月面的距离。CE-1三线阵CCD立体相机采取线中心投影方式成像[2]，前视与中视、后视与中视构成的立体交会角均为16.7°，立体相机月面分辨率为120m。
由于卫星定轨、定姿、立体相机以及激光高度计测量误差的存在，与CE-1 120m分辨率的立体相机影像相比，CE-1影像直接定位精度仍较低，月球表面模型分辨率还十分粗糙[3，4]。月球制图的主要难点在于很难精确获取月面控制点，CE-1激光高度计测距精度为5m[3]，在缺少月面控制的条件下，将高精度的激光测距作为观测值引入光束法平差，对提高定位精度具有重要意义。文献[5]中对CE-1立体相机影像与激光高度计数据不一致性进行了较为深入的分析，指出在缺少月面高精度控制点的情况下，将CE-1激光高度计测距观测值引入光束法区域网平差，作为尺度控制约束条件[6]，可以有效地约束影像外方位元素与月面点坐标之间的几何关系，提高定位精度。
本文首先阐述了CE-1姿轨数据预处理的方法，在分析立体相机外定向参数模型的基础上，建立了立体相机影像数据与激光高度计数据的联合平差数学模型。
2 姿轨数据预处理CE-1卫星定轨由统一S波段(USB)测距测速和甚长基线干涉(VLBI)测量基于J2000惯性系联合确定[7]，卫星姿态采用星敏感器在轨姿态测量控制。根据IAU/IAG行星旋转参数[8]的定义，对卫星定轨、定姿等辅助数据进行预处理，计算相机在月固坐标系中的外定向参数，作为影像联合平差的初始外定向元素。
设t为J2000参考框架标准历元；[XS(t)YS(t)ZS(t)]J2000T表示卫星在J2000坐标系中的位置矢量;[XM(t)YM(t)ZM(t)]J2000T表示月球质心在J2000坐标系中的位置矢量；RJ2000Moon表示J2000到月球坐标系旋转矩阵[8]。卫星在月球坐标系(IAU_Moon)中的位置矢量[XS(t)YS(t)ZS(t)]MoonT可由式(1)计算
设卫星本体坐标系相对月球坐标系的旋转矩阵表示为RBodyMoon(t)，RTLSBody是立体相机的安置矩阵，则立体相机相对月球坐标系的旋转矩阵RTLSBody可用式(2)计算
3 外定向参数模型
线阵相机采用推扫式的线中心投影成像，不同的线阵影像具有不同的外方位元素，空中三角测量不可能解算每条线阵影像的外方位元素[9]。因此，在线阵影像光束法平差中，通常采用分段多项式内插或定向片的方法建立平差的数学模型[10, 11]。定向片方法进行平差的基本思想是，在线阵影像上按一定时间间隔抽取若干定向影像(可视为中心投影的像片)作定向片，建立外定向参数模型；利用扩展的、基于定向片的共线条件方程建立平差函数模型，平差解算每个定向片的6个外方位元素；根据定向片内插其余线阵影像的外方位元素。
外定向参数模型描述立体相机扫描线影像外方位元素随时间的变化。卫星线阵影像平差时，任意扫描线影像的外方位元素可表示为邻近定向片外方位元素的函数。试验表明，利用邻近的4个定向片，采用3阶Lagrange多项式内插计算精度最高[12]。
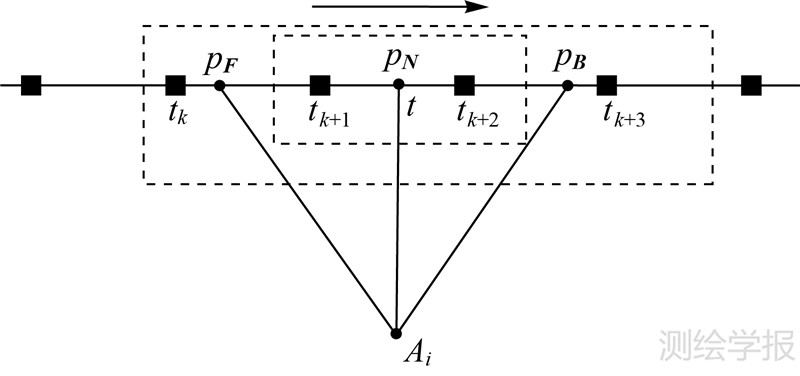
本文针对CE-1卫星近似圆形卫星轨道，考虑长条带线阵影像平差的需要，提出一种改进的立体相机外定向参数模型。将外方位定向参数模型分解为线元素内插模型及角元素内插模型。利用4个邻近定向片，采用3阶Lagrange多项式模型(LPM)建立线元素内插模型；考虑CE-1卫星近似圆形卫星轨道的特点、四元数能够方便地描述卫星姿态的变化[13, 14]，本文利用邻近的两个定向片，采用四元数球面线性内插模型(slerp)建立外定向角元素模型。此外，该模型具有计算速度快、可避免平差过程中角元素解算奇异性问题的优点。改进的内插方法能够在任意时刻计算每个扫描线影像的6个外定向参数，外定向参数建模的原理如图 1所示。图中，符号 “■”表示沿轨方向在影像上抽取的定向片影像。
|
| 图 1 外定向参数建模原理 Fig. 1 The camera exterior orientation modeling pattern diagram |
图 1中，pN表示t时刻物方点Ai在中视线阵影像上成像，邻近4个定向片分别对应成像时刻tk、tk+1、tk+2、tk+3,则pN点所在线阵影像的外方位线元素，利用邻近4个定向片内插表示
式中，XS、YS、ZS为t时刻pN点所在线阵影像的外方位线元素；Xj、Yj、Zj表示第j个定向片在tj时刻对应的外方位线元素；λj表示3阶Lagrange多项式系数，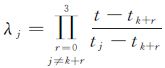
对式(3)两边取微分，可得微分关系式(4)
同理，可得前视、后视对应像点pF、pBp的相应线元素内插表达式及微分关系式。
考虑四元数在表达空间运动目标旋转时，具有姿态光滑、平稳的优点，本文采用单位四元数建立相机的姿态模型[9, 15, 16]
图 1中，pN点所在线阵影像的外方位角元素，取相邻两个定向片，分别对应成像时刻tk+1、tk+2,按照四元数球面线性内插[17]公式(5)表示
式中，qk+1=[ak+1bk+1ck+1dk+1](|qk+1|=1) 表示对应第k+1个定向片的单位四元数；qk+2=[ak+2bk+2ck+2dk+2](|qk+2|=1)表示对应第k+2个定向片的单位四元数；θ=arccos(ak+1ak+2+bk+1bk+2+ck+1ck+2+dk+1dk+2),表示上述两个单位四元数之间的夹角；t为pN点成像时刻t的归一化表示，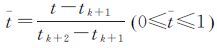
; q(|q|=1)表示pN点在成像时刻t的单位四元数。
对式(5)两边全微分，得到定向片与内插线阵之间的四元数微分关系式(6)
式中，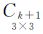
和
分别表示微分关系系数。
同样方法，可得前视、后视对应像点pF、pB的相应姿态内插表达式及微分关系式。
4 联合平差数学模型将激光高度计测距引入光束法区域网平差，进行联合平差，精化立体相机外方位元素。联合平差观测值包括连接点和激光脚印像点坐标、激光测距数值、立体相机外方位元素、激光脚印月面坐标，根据卫星测控精度、激光测距精度，确定观测值相应的先验方差，建立观测值误差方程。
4.1 影像坐标观测值影像坐标观测值包括影像连接点和激光脚印影像点两种观测值。平差连接点坐标由影像匹配获取；激光脚印影像点坐标通过影像与激光数据的配准即反投影算法[18]计算得到。影像坐标与月面点坐标关系满足共线条件方程[19]式(7)
式中，xij、yij表示第i点在第j行扫描线阵影像上的像平面坐标；f表示立体相机主距；Xi、Yi、Zi表示第i点的月面三维月固坐标；Xj、Yj、Zj表示i点所在的第j行扫描线阵影像外方位线元素；λij表示比例因子； R(qj)表示对应第j行扫描线阵影像的旋转矩阵；qj表示第j行扫描线阵影像对应的单位四元数。
将式(7)中xij、yij线性化展开，取未知数一次项，得到误差方程式(8)
式中，vxij和vyij表示第i点在第j行扫描线阵影像上的像平面坐标观测值改正数；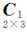
表示第i点月面点坐标未知数系数矩阵；
表示第j行扫描线阵影像对应的角元素(用四元数表示)未知数改正数系数矩阵；ΔXi、ΔYi、ΔZi 为第i点的月面三维月固坐标未知数改正数；ΔXj、ΔYj、ΔZj表示第j行扫描线阵影像外方位线元素未知数改正数；Δaj、Δbj、Δcj表示第j行扫描线阵影像四元数未知数分量改正数；xij－xij0和 yij－yij0分别表示误差方程常数项。
考虑式(3)、式(5)、式(7)可以表示为月面点坐标、4个邻近定向片外方位元素的函数。将式(4)和式(6)分别替代式(8)中微分项Δaj、Δbj、Δcj、ΔXj、ΔYj、ΔZj，可推得扩展的共线条件误差方程。
光束法联合平差中，平差连接点观测值取单位权1；激光脚印影像点观测值的定权参考文献[5]。
4.2 激光测距观测值激光测距被视为非摄影测量观测值引入三线阵影像光束法平差，作为平差尺度控制约束条件，欧式空间距离方程式表示如下
式中，Xm、Ym、Zm表示第m个激光脚印的月面坐标；Xmj、Ymj、Zmj表示第m个激光脚印所在线阵影像第j行的外方位线元素；ρm(t)表示时刻t激光测距值。
将上式线性化，得误差方程式(10)
式中，ΔXm、ΔYm、ΔZm表示第m个激光脚印的月面坐标未知数改正数；ΔXmj、ΔYmj、ΔZmj表示第m个激光脚印所在线阵影像第j行的外方位线元素未知数改正数；(ρm－ρm0)表示常数项；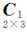
表示第m个激光脚印的月面坐标未知数改正数系数；表示线阵影像第j行的外方位线元素未知数改正数系数。
如图 1所示，若激光脉冲发射时刻t位于4个定向片成像时刻tk、tk+1、tk+2、tk+3中间，用式(4)替代式(10)中微分项ΔXmj、ΔYmj、ΔZmj，则可得到激光测距误差方程。
据文献[3]可知，CE-1激光测距精度为5m，作为距离ρ观测值的定权依据。
4.3 虚拟观测值平差之前，除像点坐标和激光测距外，初始外定向参数以及月面点(连接点和激光脚印)近似坐标是已知的。因此，为提高平差解算的稳定性及定位精度，在光束法平差过程中，可以作为加权观测值建立虚拟观测值方程参与平差[20]。虚拟观测值方程以及虚拟观测值误差方程表示形式如下
式中，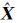
1 表示月面坐标平差值；X1OBS表示月面坐标虚拟观测值；X10表示月面坐标未知数初始值；v1表示月面坐标虚拟观测值改正数；δ1表示月面坐标未知数改正数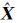；2表示定向片外方位元素平差值；X2OBS表示定向片外方位元素虚拟观测值；X2OBS表示定向片外方位元素未知数初始值；v2表示定向片外方位元素虚拟观测值改正数；δ2表示定向片外方位元素未知数改正数。
定向片外方位元素定权由卫星测控精度确定，定轨精度按350m计算；激光脚印月面坐标定权与连接点相比，具有较高的权重，激光脚印月面坐标精度按500m计算；连接点坐标作为自由未知数处理。
综上分析，式(8)、式(10)及式(12)联立构成联合平差数学模型。
5 试 验本文选取CE-1 268/269/270/271轨道 4个相邻异轨影像数据进行试验。轨道覆盖月面范围均在-70°S—+70°N，影像长度分别为36385行、35668行、36385行和36385行。试验内容包括3个部分，利用激光测高数据与影像配准，提取月面“激光脚印”的影像坐标；激光测高数据约束的联合平差；相邻异轨影像的拼接。
5.1 激光测高数据与影像配准激光测高数据与影像配准的目的是将“激光脚印”数据点反投影到影像上，并确定月面激光脚印在影像上的位置，为联合平差提供控制约束。以CE-1 268轨道影像数据为例，将“激光脚印”数据分别与前视、中视及后视影像数据进行配准，如图 2所示。经分析，以中视影像为基准，前视、后视相对中视影像配准中误差小于两个像元。
|
| 图 2 激光脚印与影像配准(0.6倍率窗口影像) Fig. 2 Registration of “footprint” and CE-1 imagery |
根据影像采样频率(84ms)、立体相机成像的基高比，按照影像上间隔约500线(时间间隔约42ms)抽取定向片影像295个，对上述4个轨道进行联合平差。
4个轨道联合平差完成后，利用平差后的外方位元素，通过计算相邻轨道公共点月面坐标较差，验证联合平差模型及算法的正确性及有效性。
以269/270轨道为例，计算相邻轨道公共点月面坐标较差。269/270轨道之间提取1029个公共点。X、Y、Z坐标较差分布如图 3所示。试验表明，X、Y坐标精度分别为47.5m、51.5m,Z坐标精度为86.1m，X、Y、Z误差均小于一个像素(120m)。
|
| 图 3 轨道公共点坐标较差 Fig. 3 The difference of conjugate points coordinates between adjacent tracks |
以CE-1 268/269异轨立体相机影像为例，根据平差得到的线阵影像扫描线的外方位元素，计算影像格网点对应的月面坐标，利用平面仿射变换进行影像拼接，图 4显示拼接效果良好(绿波段影像为268轨道中视影像、红波段影像为269轨道中视影像)。
|
| 图 4 268/269轨道中视影像拼接(0.5倍率窗口影像) Fig. 4 The image mosaic of the nadir view between adjacent tracks 268 and 269 |
本文在分析研究CE-1立体相机外定向参数模型的基础上，将CE-1激光高度计数据引入光束法区域网平差，构建了联合平差数学模型。立体相机外定向参数模型方面，根据 CE-1卫星的轨道特点，利用3阶Lagrange多项式模型和四元数球面线性内插模型，分别建立了不同的外方位线元素和角元素内插模型；光束法平差过程引入激光测距观测值，约束影像外方位元素与月面点坐标之间的几何关系，提高了平差解算的稳定性及定位精度。由于缺少月面绝对控制，本文仅对联合平差之后轨道之间的相对定位精度进行评定。试验表明，相对定位精度小于1个像元，联合平差模型及算法是有效的。
致谢：感谢国防科工委月球探测工程中心提供嫦娥一号月球探测试验数据。
| [1] | YANG Weilian,ZHOU Wenyan. Orbit Design for Lunar Exploration Satellite CE-1[J]. Spacecraft Engineering,2007,16(6):16-24. (杨维廉,周文艳. 嫦娥一号月球探测卫星轨道设计[J]. 航天器工程,2007,16(6):16-24.) |
| [2] | ZHAO Baochang, YANG Jianfeng, WEN Desheng, et al. Design and On-orbit Measurement of Chang’E-1 Satellite CCD Stereo Camera[J]. Spacecraft Engineering, 2009, 18(1):30-36. (赵葆常,杨建峰,汶德胜,等. 嫦娥一号卫星CCD立体相机的设计与在轨运行[J].航天器工程,2009, 18(1):30-36.) |
| [3] | LI Chunlai, LIU Jianjun, REN Xin, et al. CE-1 Moon Image Data Processing and Image Mapping[J]. Scientia Sinica Terrae, 2010, 40(3):294-306. (李春来, 刘建军, 任鑫, 等. 嫦娥一号图像数据处理与全月球影像制图[J].中国科学:地球科学, 2010, 40(3):294-306.) |
| [4] | PING Jingsong, HUANG Qian, YAN Jianguo, et al. Lunar Topographic Model CLTM-s01 from Chang'E-1 Laser Altimeter[J]. Scientia Sinica Pysica,Mechanica & Astronomica, 2008, 38(11):1601-1612. (平劲松,黄倩,嫣建国,等.基于嫦娥一号卫星激光测高观测的月球地形模型CLTM一s0l[J].中国科学G辑:物理学 力学 天文学,2008, 38(11):1601-1612.) |
| [5] | ZHAO Shuangming ,LI Deren ,MOU Lingli.Inconsistency Analysis of CE-1 Stereo Camera Images and Laser Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica,2011,40(6):751-755.(赵双明,李德仁,牟伶俐. CE-1立体相机影像与激光高度计数据不一致性分析[J].测绘学报,2011,40(6):751-755.) |
| [6] | DONALD L L. Photo geodesy from Apollo[C]//Fall Convention of the American Society of Photogrammetry. San Francisco:[s.n.],1971:574-587. |
| [7] | CHEN Ming, TANG Geshi, CAO Jianfeng, et al. Precision Orbit Determilllation of CE-l Lunar Satellite[J]. Geomatics and Information Science of Wuhan University, 2011,36(2):212-216.(陈明, 唐歌实,曹建峰, 等. 嫦娥一号绕月探测卫星精密定轨实现[J]. 武汉大学学报:信息科学版, 2011, 36(2):212-216.) |
| [8] | SEIDELMANN P K. Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites:2000[J]. Celestial Mechanics and Dynamical Astronomy, 2002, 82(1): 83-111. |
| [9] | LI Deren, ZHAO Shuangming, LU Yuhong, et al. Combined Block Adjustment for Airborne Three Line CCD Scanner Images[J]. Acta Geodaetica et Cartographica Sinica,2007,36(3):245-249.(李德仁, 赵双明, 陆宇红,等. 机载三线阵传感器影像区域网联合平差[J].测绘学报,2007,36(3):245-249.) |
| [10] | ZHAO Shuangming, LI Deren. Experimentation of Adjustment Math Model for ADS40 Sensor[J]. Acta Geodaetica et Cartographica Sinica,2006, 35(4):342-346.(赵双明,李德仁. ADS40 机载数字传感器平差数学模型及其试验[J]. 测绘学报,2006, 35(4):342-346.) |
| [11] | CHANGNO L, HENRY J, THEISS J S B,et al. Rigorous Mathematical Modeling of Airborne Pushbroom Imaging Systems[J].Photogrammetry Engineering and Remote Sensing, 2000, 66(4):385-392. |
| [12] | EBNER H, KORNUS W, OHLHOF T. A Simulation Study on Point Determination for the MOMS-02/D2 Space Project Using an Extended Functional Model[J]. IAPRS, 1992,29:458-464. |
| [13] | ANDREIS D,CANUTO E S. Orbit Dynamics and Kinematics with Full Quaternions[C]//Proceedings of the 2004 American Control Conference. Massachusetts: [s.n.],2004. |
| [14] | JACK C K, CHOU M. Quaternion Kinematic and Dynamic Differential Equations[J]. IEEE Transactions on Robotics and Automation, 1992,8:53-64. |
| [15] | HINSKEN L, MILLER S, TEMPELMANN U, et al. Triangulation of LH Systems’ADS40 Imagery Using ORIMA GPS/IMU[C]//Proceedings of ISPRS Commission Ⅲ. Graz:[s.n.],2002. |
| [16] | LIU Jun, WANG Donghong, ZHANG Yongsheng. Triangulation of Airboren Three-line Images Using Unit Quaternion [C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:[s.n.],2008. |
| [17] | KEN S. Animating Rotation with Quaternion Curves[J]. ACM SIGGRAPH Computer Graphics, 1985,19(3):245-254. |
| [18] | ZHAO Shuangming, RAN Xiaoya, GUO Xinhong. CE-1 Stereo Camera Imaging Geometry Model[J].Science of Surveying and Mapping,2011,36(6):112-114. (赵双明,冉晓雅,郭芯宏. CE-1立体相机成像几何模型研究[J], 测绘科学,2011,36(6):112-114.) |
| [19] | LI Deren, ZHENG Zhaobao. Analytical Photogrammetry [M]. Beijing: Survey and Mapping Press, 1992.( 李德仁, 郑肇葆. 解析摄影测量学[M]. 北京:测绘出版社,1992.) |
| [20] | MCGLONE J C, EDWARD M M, JAMES S B, et al. Manual of Photogrammetry[M]. Maryland:The American Society for Photogrammetry and Remote Sensing,2004:848-852. |