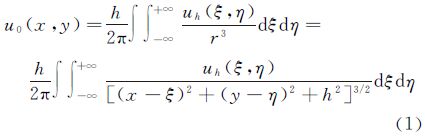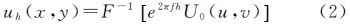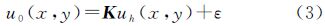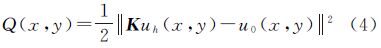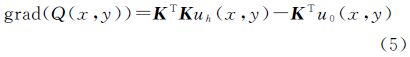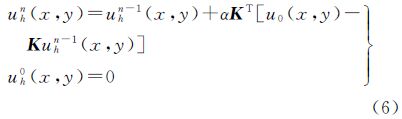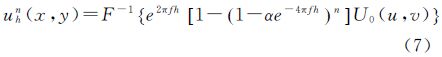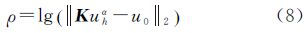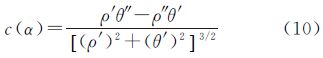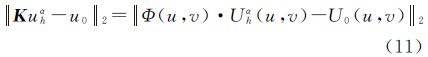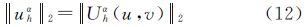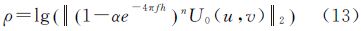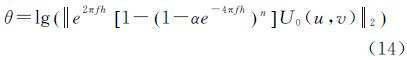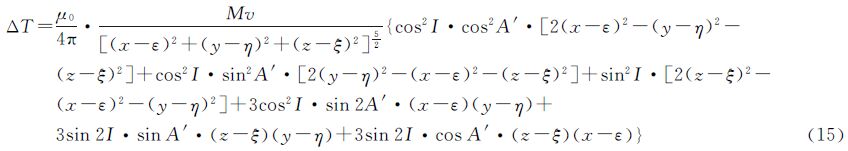2. 地理信息工程国家重点实验室,陕西 西安 710054;
3. 武汉大学 地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079
2. State Key Laboratory of Geo-Information Engineering,Xi’an 710054,China;
3. Key laboratory of Geo-space Environment and Geodesy of Ministry of Education,Wuhan University,Wuhan 430079,China
1 引 言
在实际工作中,航空重力与磁力测量通常是在起伏的航线上进行的。然而重力与磁力资料的定量解释方法一般要求测量数据分布在一个平面上,因此需要将实测资料换算到一个平面上。
重力与磁力测量数据的向下延拓直接关系到这些数据的处理及反演方法的应用效果。利用向下延拓可以把重力与磁力测量数据的观测面外推到场源体附近,突出局部场,有利于提高重力与磁力测量数据解释的可靠性。然而,向下延拓是一个典型的不适定问题,主要表现为计算的不稳定性。随着向下延拓深度的增大,会对重力与磁力测量数据中的高频干扰信号起着显著的放大作用,导致不能分辨有效信号。
目前处理不适定问题的主要方法是采用正则化技术,国内外学者也作了大量的研究。文献[1]采用正则化技术研究了位场数据的向下延拓,并推导出了稳定的频率域延拓算子;文献[2]讨论了正则化方法位场向下延拓的4个频率响应公式;文献[3]介绍了解决非线性病态性问题的改进Landweber迭代法的收敛分析;文献[4]评述了向下延拓及其基于Tikhonov正则化算法的正则化过程;文献[5]研究了航空和地表重力数据向下延拓的几种正则化方法;文献[6]基于Poisson积分方程,给出了向下延拓的正则化算法;文献[7]采用正则化方法中的Landweber迭代法来处理不适定问题;文献[8, 9]结合Tikhonov正则化算法和移去-恢复技术对航空重力测量数据进行了向下延拓的仿真试验;文献[10]根据逆Poisson积分方程,采用L曲线法确定Tikhonov正则化参数;文献[11]研究了位场数据的正则化向下延拓法,并考虑了几种有统计学意义的正则化方案;文献[12]研究了迭代正则化方法(包括迭代Tikhonov法、Landweber迭代法和截断奇异值分解法)在位场下延中的应用;文献[13]比较3种正则化参数的选取方法;文献[14]推导了积分迭代法对应的正则化滤波子函数;文献[15]探讨了3种空间域迭代解法在位场向下延拓中的异同和各自优势;文献[16]提出了Tikhonov双参数正则化法;文献[17]提出将广义岭估计用于求解航空重力向下延拓病态问题,研究了求解逆Poisson积分问题的3种正则化方法。
在向下延拓的正则化方法研究中,正则化参数的确定是一项非常重要的任务,参数选择的优劣直接影响了最终延拓结果的精度。目前,许多重力与磁力测量数据向下延拓方法都使用了正则化技术。然而,最佳正则化因子的确定,在模拟试验中是在延拓面数据已知的情况下根据最小延拓误差来估算的。而对于实际的重力与磁力测量数据向下延拓,延拓面并不一定存在已知的测量数据。因此,在这种情况下如何确定最优正则化参数,是应该重点研究的问题。总体来说,在目前的重力与磁力测量数据向下延拓的正则化技术研究中,有关正则化参数确定方法的研究较少。因此,最优正则化参数的确定问题研究具有重要意义。
本文根据观测面和延拓面重力与磁力测量数据的Poisson积分平面近似关系,结合快速傅里叶变换算法,将其转换到频率域进行计算。为了克服计算的不稳定性并提高计算结果的精度,引入Landweber正则化迭代法,在此基础上采用L曲线法研究磁力数据向下延拓中最优正则化参数的确定。
2 重力与磁力测量数据向下延拓的基础模型重力与磁力测量数据向下延拓的基本原理如图 1所示。

|
| 图 1 向下延拓示意图 Fig. 1 Downward continuation sketch map |
u0(x,y)表示观测面上的重力与磁力测量数据,uh(ξ,η)表示延拓面上的重力与磁力测量数据,计算观测面以下至场源以上空间z=h平面的重力与磁力测量数据,这种换算称为重力与磁力测量数据向下延拓。
根据重力与磁力测量数据向上延拓公式,得到观测面重力与磁力测量数据u0(x,y)与向下延拓面重力与磁力数据uh(x,y)之间的平面近似关系为[19]
式中,h是向下延拓深度;r是延拓面上点(ξ,η,h)与观测面上点(x,y,0)之间的距离。对上式进行傅里叶变换,经过整理,得到向下延拓的基本原理公式
式中,f=(u2+v2)1/2,u、v为波数,分别表示空域变量x、y对应的频域变量。从式(2)可以看出,由于向下延拓算子e2πfh的不稳定性,会对重力与磁力测量数据中的高频噪声有着显著的放大作用,在延拓深度较大时导致延拓结果精度不高,为了解决这种不适定问题,需要引入正则化因子,因此,研究了Landweber正则化迭代法数学模型。
式(1)可以修改为
式中,K表示第一类Fredholm积分算子;ε表示平面近似误差。由式(2)可知,重力与磁力测量数据向下延拓即为求解uh(x,y),并使得目标函数
最小,以求得最小平方解。函数Q(x,y)的最速下降方向亦即梯度,即 Landweber正则化迭代法是最速下降法的一种变形,其迭代形式如下对式(6)两端进行傅里叶变换,并由数学归纳法,经过调整,即可得到重力与磁力测量数据向下延拓的Landweber正则化迭代法公式为[3, 14, 15]
利用式(7)进行重力与磁力测量数据的向下延拓时,如果是采用仿真数据,则可以根据观测面和延拓面的仿真数据来求解其最优正则化参数,但在处理实测数据时,最优正则化参数的确定就需要采用其他方法,本文使用的是L曲线法。
3 L曲线法在实测重力与磁力测量数据的噪声水平未知的情况下,可以采用L曲线法来确定正则化参数。根据式(3),L曲线法采用对数尺度描述拟合误差||Kuhα-u0||2与正则解||uhα||2随参数α变化的对比曲线,它的特征是曲线呈明显的大写字母“L”形,并根据其轨点来确定正则化参数α*[18]。令 则L曲线的曲率函数c(α)定义为 式中,“′”、“″”分别表示ρ、θ关于参数α的一阶和二阶导数。
将拟合误差||Kuhα-u0||2与正则解||uhα||2转换到频率域,有
则对于Landweber正则化迭代法,根据式(7),有
利用一阶和二阶差分可以得到ρ和θ的一阶和二阶导数。根据给定的α值,利用FFT算法,可快速计算得到相应的c(α)序列,绘成曲线后其极大值所对应的正则化参数即为确定的正则化参数α*。
4 数值试验与结果分析本文在数值试验时,以磁力测量数据为例来对最优正则化参数的确定方法进行研究。
4.1 试验数据仿真利用球体磁场模型计算磁异常的公式为[20]
式中,μ0为真空中的磁导率,μ0=4π×10-7H/m;M为磁化强度;v为球体模型的体积;I为磁化倾角;A′为磁化偏角;(ε,η,ξ)为球心点坐标;(x,y,z)为空间一点的坐标。为了增加磁力试验数据的复杂性,本文共设计了4个不同位置、不同埋深的球体磁场模型,并将其产生的磁异常进行叠加。球体磁场模型采用的基本参数如表 1所示。
| 球体半径/m | 磁化强度/(A/m) | 磁化倾角/(°) | 磁化偏角/(°) |
| 300.0 | 100.0 | 45 | 30 |
球体磁场模型采用的球心坐标如表 2所示。
| 球体磁场模型 | x | y | z |
| 模型1 | 2 000.0 | 2 000.0 | 2 000.0 |
| 模型2 | 2 000.0 | -2 000.0 | 2 100.0 |
| 模型3 | -2 000.0 | -2 000.0 | 2 200.0 |
| 模型4 | -2 000.0 | 2 000.0 | 2 300.0 |
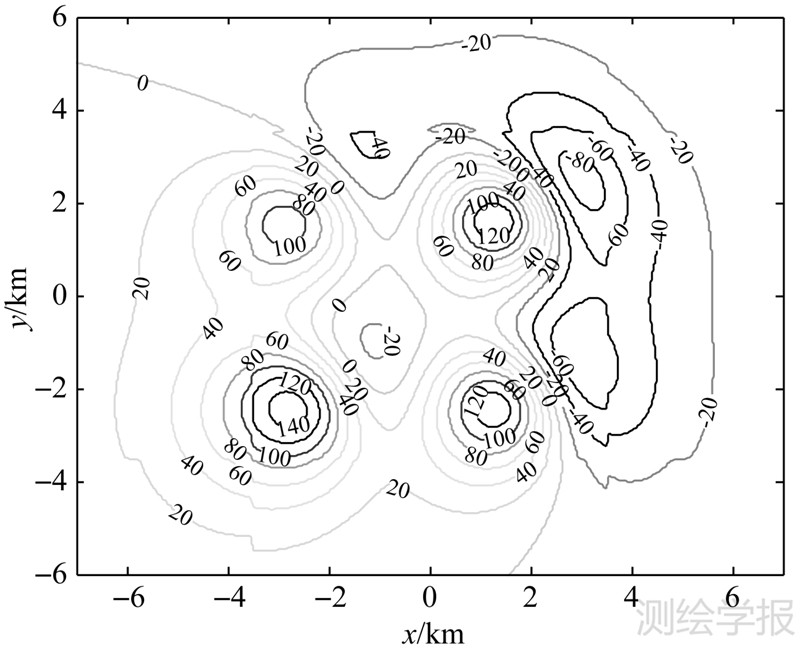
磁异常数据的格网分辨率为50m×50m,点数为221×221。根据球体磁场公式分别计算z=0m和z=300m两个不同观测面上的理论磁异常数据。图 2、图 3分别为观测面z=0m和z=300m的理论磁异常数据等值线图。为了验证本文确定最优正则化参数方法的有效性,在z=0m观测面理论磁异常数据中加入均值为0、方差为3nT的高斯白噪声,其等值线图如图 4所示。
|
| 图 2 观测面z=0m的理论磁异常数据等值线(单位:nT) Fig. 2 Isoline figure of theoretical magnetic anomaly data on the plane of z=0m(unit:nT) |

|
| 图 3 观测面z=300m的理论磁异常数据等值线图(单位:nT) Fig. 3 Isoline figure of theoretical magnetic anomaly data on the plane of z=300m(unit:nT) |

|
| 图 4 z=0m观测面加入3 nT高斯白噪声后的理论磁异常数据等值线图(单位:nT) Fig. 4 Isoline of theoretical magnetic anomaly data added with 3 nT white noise on the plane of z=0m (unit:nT) |
其统计特性如表 3所示。
| 观测面高度/m | 最大值/nT | 最小值/nT | 平均值/nT | 标准差/nT |
| 0(无噪声) | 150.190 | -87.551 | 4.280 | 34.575 |
| 0(有噪声) | 151.634 | -91.435 | 4.286 | 34.615 |
| 300 | 245.835 | -134.627 | 4.472 | 47.504 |
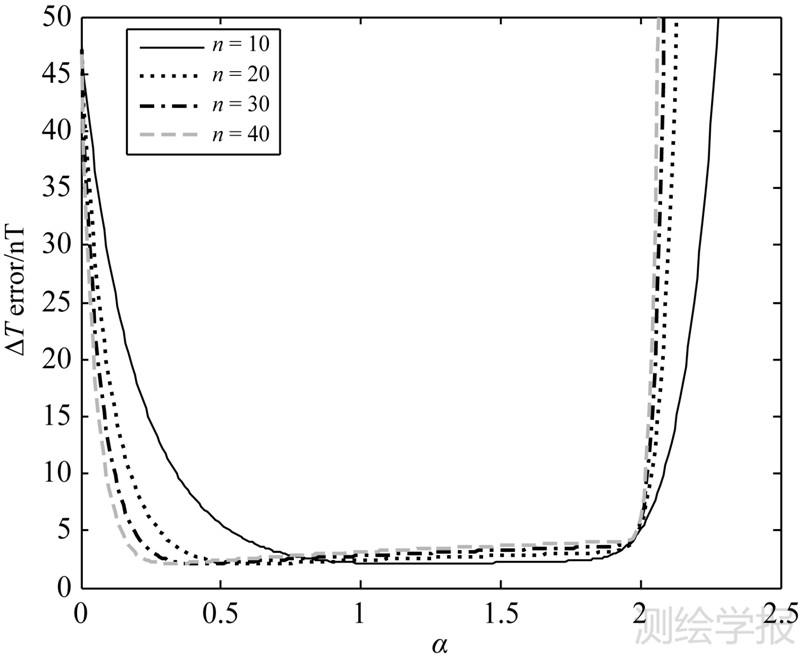
在对Landweber正则化迭代法的延拓精度进行测试时,首先需要对延拓误差与正则化因子及迭代次数的关系进行验证。具体计算时,取正则化因子分别为α=0.5、1.0、1.5、2.0。延拓误差与迭代次数的关系如图 5所示。当迭代次数分别取10次、20次、30次和40次时,延拓误差与正则化因子的关系如图 6所示。

|
| 图 5 延拓误差与迭代次数的关系图 Fig. 5 Relationship figure of continuation error and iteration times |
|
| 图 6 延拓误差与正则化因子的关系图 Fig. 6 Relationship figure of continuation error and regularization factors |
从图 5可以看出,对于不同的正则化因子,Landweber正则化迭代法在曲线的拐点处取得了最小的延拓误差。但是当正则化因子α=2.0时,延拓误差突然增大,因此可以得知,选取的正则化因子不宜过大,以小于2.0为宜。
从图 6可以看出,迭代次数越多时,在取得最小延拓误差处对应的正则化因子越小。另外,在正则化因子大于2.0时,可以看到延拓误差急剧增大,这与图 5显示的结果相符,说明在采用Landweber正则化迭代法进行磁场数据向下延拓时,正则化因子应该小于2.0。
表 4表示Landweber正则化迭代法在延拓结果取得最小延拓误差时对应的正则化因子和迭代次数。
| 正则化因子α | 迭代次数n | 最大值 | 最小值 | 平均值 | 均方差 |
| 1.171 | 10 | 14.507 | -8.133 | 0.186 | 2.101 |
| 0.621 | 20 | 14.482 | -8.361 | 0.186 | 2.113 |
| 0.421 | 30 | 14.571 | -8.417 | 0.186 | 2.118 |
| 0.321 | 40 | 14.408 | -8.499 | 0.186 | 2.121 |
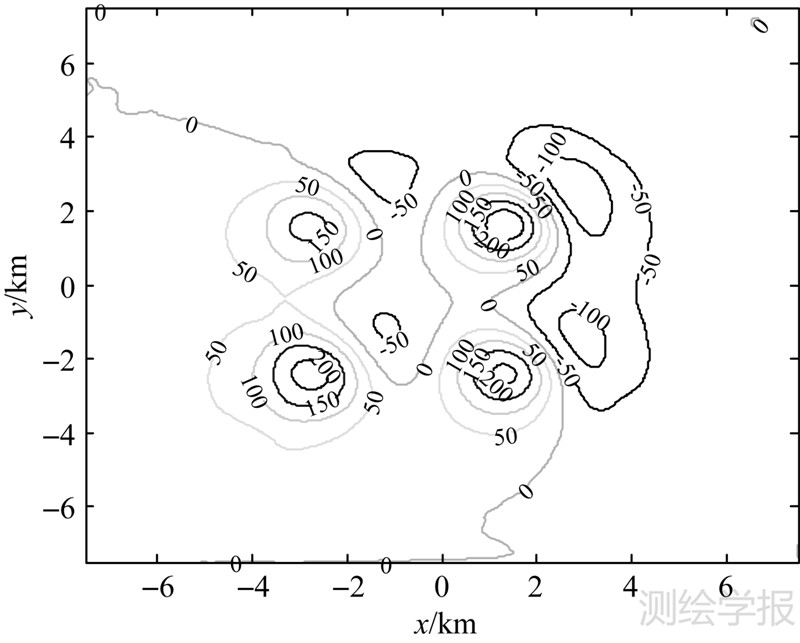
图 7给出了Landweber正则化迭代法在取得最小延拓误差(即α=1.171)时对应的延拓结果等值线图。
|
| 图 7 延拓结果等值线图(单位:nT) Fig. 7 Isoline figure of continuation results(unit:nT) |
从图 3、图 7比较看,Landweber正则化迭代法延拓结果对延拓面上理论磁异常数据的逼近效果很好。
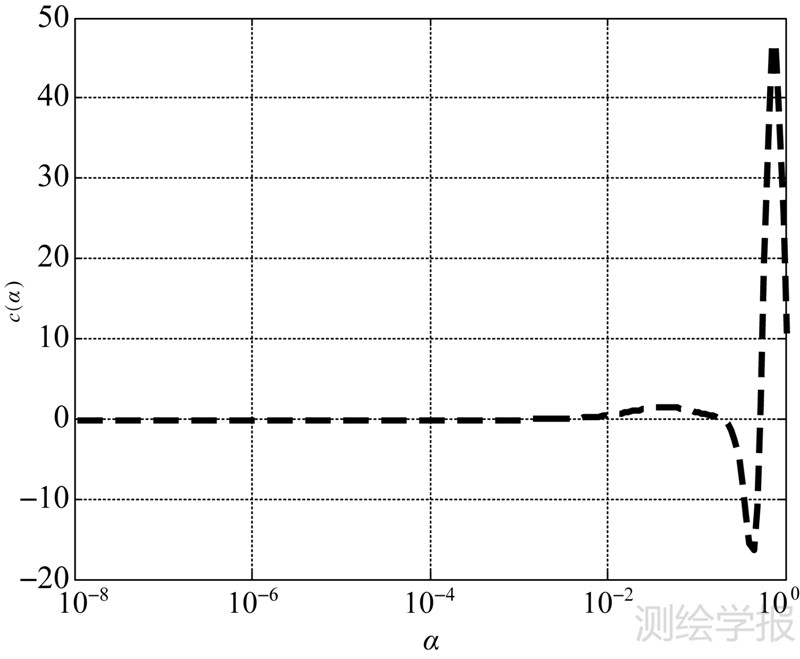
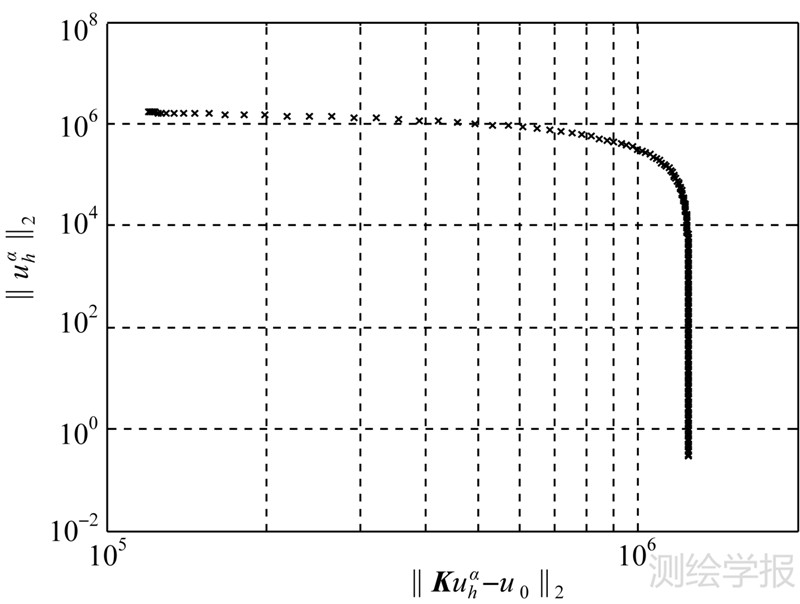
4.3 L曲线法试验结果图 8和图 9分别为迭代次数取30时Landweber正则化迭代法对应的曲率函数图和L曲线图,图 8中曲率最大值点即对应着最优正则化参数,也就是图 9中L曲线中的拐点处,有趣的是图 9中的曲线形状为倒L型。从图 8可知,α*=0.732,将α*代入式(7),可以得到L曲线法选取的正则化因子对应的延拓结果,其等值线图如图 10所示。
|
| 图 8 曲率函数图 Fig. 8 Curvature function figure |
|
| 图 9 L曲线图 Fig. 9 L-curve figure |

|
| 图 10 L曲线法选取的正则化因子对应延拓结果的等值线图(单位:nT) Fig. 10 Isoline figure of the continuation results corresponding to regularization factor chosen by L-curve method(unit:nT) |
由图 10和图 3的比较可以看出,Landweber正则化迭代法中,根据L曲线法确定的最优正则化因子,其对应的延拓结果对延拓面上的理论磁异常数据的逼近效果较好。
表 5为延拓面数据未知时利用L曲线法选取的正则化因子对应的延拓结果精度统计情况。通过与表 4比较可以看出,本文利用L曲线法来确定正则化因子,对于Landweber正则化迭代法来说精度较好。
| 延拓方法 | 正则化因子α | 最大值 | 最小值 | 平均值 | 均方差 |
| Landweber正则化迭代法 | 0.732 | 13.511 | -12.395 | 0.186 | 2.476 |
从图 9可以看出,L曲线主要由一个“水平”的部分和一个接近“垂直”的部分组成。水平部分对应的解表示正则化参数太大,因此这部分解主要由正则化误差影响较大;垂直部分对应的解表示正则化参数太小,因此这部分解主要由观测数据误差影响较大。所以,水平部分和垂直部分分别表示过于平滑解和不太平滑解,只有曲线的拐点处则是对这两种解最好的平衡。
利用理论磁场反演实例表明:①当正则化参数小于2时,反演效果很好,当正则化参数大于2时,反演效果迅速变差;②当正则化参数处于[0.7,2]区间时,反演效率最好,因为只需10步反演就能取得精确的结果;③当正则化参数小于2时,反演效果均不错,而L曲线法确定的正则化参数(0.732)亦小于2,这也说明了L曲线法在确定正则化参数时的有效性。
5 结 论本文采用L曲线法研究了Landweber正则化迭代法中最优正则化参数的确定问题,并通过模型磁测数据验证了L曲线法在确定正则化参数时的有效性。重力测量数据与磁力测量数据同属于位场数据,因此,L曲线法在重力测量数据的正则化向下延拓中也同样适用,只是其确定的正则化参数会有所不同。
对于正则化参数的确定,当观测数据噪声水平已知时,可以通过偏差原理、广义偏差原理、Arcangeli准则等方法确定;当数据噪声水平未知时,可以通过拟最优准则、广义交叉检验准则、L曲线准则等方法来确定。本文仅研究了L曲线法,还需要对其他方法的适用性进行试验。
| [1] | TIKHONOV A N, ARSENIN V Y. Solution of Certain Integral Equations of the First Kind[J]. Journal of Associate Computer Machine, 1962 (9): 84-97. |
| [2] | LIANG Jinwen. Downward Continuation of Regularization Methods for Potential Fields[J]. Chinese Journal of Geophysics, 1989, 32(5): 600-608. (梁锦文. 位场向下延拓的正则化方法[J]. 地球物理学报, 1989, 32(5): 600-608.) |
| [3] | SCHERZER O. A Modified Landweber Iteration for Solving Parameter Estimation Problems[J]. Application of Math Optim, 1998, 38: 45-68. |
| [4] | ILK K H, KUSCHE J, RUDOLPH S. A Contribution to Data Combination in Ill-posed Downward Continuation Problems[J]. Journal of Geodynamics, 2002, 33:75-99. |
| [5] | KERN M. An Analysis of the Combination and Downward Continuation of Satellite, Airborne and Terrestrial Gravity Data[R]. Calgary: University of Calgary, 2003. |
| [6] | WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J].Acta Geodaetica et Cartographica Sinica, 2004,33(1):33-38.(王兴涛,石磐,朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解[J].测绘学报,2004,33(1):33-38.) |
| [7] | CHEN Longwei, ZHANG Hui, ZHENG Zhiqiang, et al. Technique of Geomagnetic Field Continuation in Underwater Geomagnetic Aided Navigation[J]. Jounral of Chinese Inertial Technology, 2007, 15(6): 693-697. (陈龙伟, 张辉, 郑志强, 等. 水下地磁辅助导航中地磁场延拓方法[J]. 中国惯性技术学报, 2007, 15(6): 693-697.) |
| [8] | CHEN Yi, HAO Yanling, LIU Fanming. Analysis of Effect and Downward Continuation of Airborne Gravity Data[J]. Journal of System Simulation, 2008,20(8):2190-2194.(成怡,郝燕玲,刘繁明.航空重力测量数据向下延拓及其影响因素分析[J].系统仿真学报,2008,20(8):2190-2194.) |
| [9] | HAO Yanling, CHEN Yi, SUN Feng, et al. Simulation Research on Tikhonov Regularization Algorithm in Downward Continuation[J]. Chinese Joumal of Scientific Instrument, 2008, 29(3): 605-609. (郝燕玲,成怡,孙枫,等.Tikhonov正则化向下延拓算法仿真试验研究[J].仪器仪表学报,2008,29(3):605-609.) |
| [10] | DENG Kailiang, BAO Jingyang, HUANG Motao, et al. Simulation of Tikhonov Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Geomatics and Information Science of Wuhan University, 2010,35(12):1414-1417. (邓凯亮,暴景阳,黄谟涛,等.航空重力数据向下延拓的Tikhonov正则化法仿真研究[J].武汉大学学报:信息科学版,2010,35(12):1414-1417.) |
| [11] | FEDI M, FLORIO G. Normalized Downward Continuation of Potential Fields within the Quasi-harmonic Region[J]. Geophysical Prospecting, 2011, 59: 1087-1100. |
| [12] | ZHOU Jun, SHI Guiguo, GE Zhilei. Study of Iterative Regularization Methods for Potential Field Downward Continuation in Geophysical Navigation[J]. Journal of Astronautics, 2011, 32(4): 787-794. (周军,施桂国,葛致磊.地球物理导航中位场下延的迭代正则化方法研究[J].宇航学报,2011,32(4):787-794.) |
| [13] | YANG Mingming, LIU Daming, LIU Shengdao, et al. Submarine’s Magnetic Field Extrapolation Using Boundary Element Method and Tikhonov Regularization[J]. Acta Armamentarii, 2011, 31(9): 1216-1221. (杨明明, 刘大明, 刘胜道, 等. 采用边界积分方程和Tikhonov正则化方法延拓潜艇磁场[J]. 兵工学报, 2011, 31(9): 1216-1221.) |
| [14] | ZENG Xiaoniu, LI Xihai, LIU Daizhi, et al. Regularization Analysis of Integral Iteration Method and the Choice of Its Optimal Step Length[J]. Chinese Journal of Geophysics, 2011, 54(11): 2943-2950. (曾小牛,李夕海,刘代志,等. 积分迭代法的正则性分析及其最优步长的选择[J]. 地球物理学报, 2011, 54(11): 2943-2950.) |
| [15] | ZENG Xiaoniu, LI Xihai, HAN Shaoqing, et al. A Comparison of Three Iteration Methods for Downward Continuation of Potential Fields[J]. Progress in Geophysics, 2011, 26(3): 908-915. (曾小牛, 李夕海, 韩绍卿, 等. 位场向下延拓三种迭代方法之比较[J]. 地球物理学进展, 2011, 26(3): 908-915.) |
| [16] | DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(6):690-696. (邓凯亮,黄谟涛,暴景阳,等.向下延拓航空重力数据的tikhonov双参数正则化法[J].测绘学报,2011,40(6):690-696.) |
| [17] | JIANG Tao, LI Jiancheng, WAN Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(6):112-122. (蒋涛,李建成,王正涛,等.航空重力向下延拓病态问题的求解[J].测绘学报,2011,40(6):112-122.) |
| [18] | HANKE M, HANSEN P C. Regularization Methods for Large Scale Problems[J]. Survey on Mathematics for Industry, 1993, 3(4): 253-315. |
| [19] | WANG Xingtao, XIA Zheren, SHI Pan, ZHAI Zhenhe. A Comparison of Different Downward Continuation Methods for Airborne Gravity Data[J]. Chinese Journal of Geophysics, 2004, 47(6): 1017-1022. (王兴涛,夏哲仁,石磐,翟振和.航空重力测量数据向下延拓方法比较[J].地球物理学报,2004,47(6):1017-1022.) |
| [20] | GUAN Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing: Geological Publishing House, 2005. (管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.) |