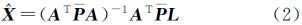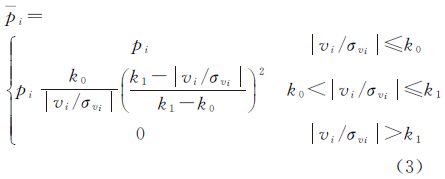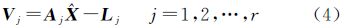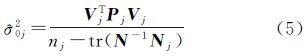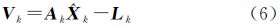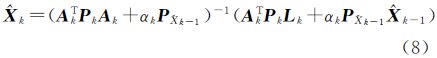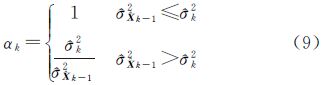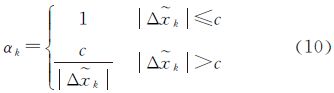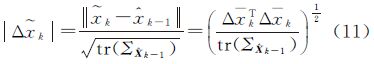2. 北京卫星导航中心，北京 100049；
3. 信息工程大学，河南 郑州 450001；
4. 西安测绘研究所，陕西 西安 710054
2. Beijing Institute of Satellite Navigation,Beijing 100049，China;
3. Information Engineering University,Zhengzhou 450001,China;
4. Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China
1 引 言
大多数自适应参数估计都基于特定的准则。基于随机模型自适应的参数估计大多与误差度量有关，不同的误差度量对应于不同的自适应估计。通常基于观测方差协方差的加权最小二乘估计可以称为内部自适应参数估计，即根据观测的内部精度自适应地调整观测对参数估值的贡献；若基于观测的外部精度自适应调整观测的贡献则可称为外部精度自适应估计；若部分根据外部信息、部分依赖内部精度调整观测对参数估计的贡献，可称为半外部精度自适应参数估计。
常用的参数最小二乘估计一般假设观测误差主要为随机误差且服从正态分布，进而基于观测验前方差协方差信息确定观测信息的权矩阵，自适应地调整观测信息对模型参数解的贡献，使模型参数估计最佳地适应于观测精度。从随机模型自适应调整角度，这类估计主要采用内部观测方差协方差作为观测权的统计量，于是，这类参数估计可以称为内部精度自适应参数估计。相应的参数估计有最小二乘参数估计、拟合推估(Collocation)[1, 2]、Bayes估计[3]、Kalman滤波等。当观测信息的验前统计信息可靠，观测误差服从正态分布，则参数最小二乘估计满足无偏、一致、有效性。但是，当观测验前统计模型不可靠，则观测对参数解的贡献的分配将不再合理。
为了合理调整各类观测量对模型参数的贡献，在大地测量及统计学界常采用方差分量估计方法[4, 5, 6, 7, 8, 9, 10, 11]，自适应地调整不同类型或不同组观测量之间的权比。由于方差分量估计的统计量含有本组观测信息和其他组观测信息，于是这类自适应随机模型的调整可以称为半外部精度自适应估计。
为了控制个别异常观测对模型参数估计的影响，一般采用抗差估计自适应地调整异常观测的贡献[12, 13, 14]。抗差估计一般是利用相应观测的残差构造权函数，于是也属于半外部自适应参数估计。
实践中，实时观测信息的可靠性一般高于先验信息，高于模型预测信息，于是，为了合理平衡实时观测信息与先验信息对模型参数估计的贡献，往往依据实时观测信息自适应地调整先验信息的贡献，这类自适应估计有自适应Kalman滤波[15, 16, 17]、附有条件的自适应滤波[18]、自适应拟合推估[19, 20]和自适应序贯平差[21]等。这类自适应估计可以称为外部自适应参数估计。
2 半外部精度自适应估计类半外部精度自适应估计类主要指参数估计过程中自适应随机模型统计量含有本观测信息。按照这一描述，大多数抗差估计、方差分量估计均属于半外部精度自适应估计类。
2.1 抗差估计设观测误差方程为
式中，L为n×1维观测向量；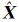
为m×1维模型参数估值向量；V为n×1维观测残差向量；A为n×m维设计矩阵。再假设观测协方差矩阵为Σ，其对角线元素为σi2；观测权矩阵为P=σ02Σ－1，参数抗差估计解为
式中，P为等价权矩阵，若采用IGGⅢ权函数，元素为[11, 3]
式中，σvi为残差vi的均方差；k0和k1为控制因子，k0一般取1.0～1.5，k1一般取3.0～8.5。
从等价权元素可见，观测量的权取决于标准化残差vi/σvi的大小，标准化残差越大，相应观测量的权越小。这类观测等价权不是完全由观测内部精度决定的，它一方面取决于内部精度，即σvi和pi，还取决于观测残差vi的大小，或本观测与观测总体的偏离程度。由于观测权的确定具有自适应性，于是这类参数估计可以称为半外部精度自适应估计。
这类半外部精度自适应估计与纯内部精度自适应估计的显著区别在于，观测权不仅由内部方差确定，也由本观测与其他观测的离差进行自适应调整。如果观测内部精度很高，则基于内部精度自适应估计的观测权一般较大，但如果某观测残差较大，则利用等价权进行调整，相应观测的权将减小，因而该观测对参数估计的贡献也随之减小。
2.2 方差分量估计方差分量估计的典型形式是Helmert型估计[11]。假设有r组观测L1，L2，…，Lr，相应误差方程为
近似Helmert方差分量估计公式为[6, 11, 22] 式中，nj为第j组观测值的个数；Nj为对应的法矩阵；N－1为总法矩阵的逆阵。应该注意，Nj必须增广到与N的维数相同，而且未知参数的顺序也必须相同。
由于上述Helmert类方差分量估计是用来自适应调整各类观测权的过渡因子，其中Vj是本组观测相对于整体参数估计的残差向量，而整体参数估计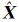含有全部观测向量的信息，当然也含有本组部分观测Lj的贡献，即
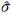0j2含有部分外部精度和内部精度信息，因此称其为半外部精度自适应估计。
基于方差分量估计的参数估计与传统参数估计的显著区别正是在于，观测向量对参数解的贡献不再完全由先验内部精度唯一确定，而是利用本组观测与整体观测的偏差重新确定方差分量，并重新调整本组观测相对于其他观测的权比，从而更合理地平衡各类观测对参数估计的贡献。
当然，如果采用条件闭合差求定各类观测方差分量，再确定相应观测量的权矩阵[7, 23]，则该类方差分量估计所对应的自适应参数估计类又变成了外部精度自适应参数估计类。因为外部条件闭合差确定的精度属于外部精度。
3 外部精度自适应估计类外部精度自适应估计是指随机模型的调整由随机参量与外部参考信息的离散度确定。典型的外部精度自适应估计有自适应Kalman滤波[15, 16]、自适应拟合推估[19, 20]等。最简单的外部精度自适应估计是动态数据的序贯平差。
设tk观测向量为Lk，相应误差方程为
式中，Ak为nk×m维设计矩阵，也称观测矩阵；Vk为nk×1维观测残差向量。
基于内部精度自适应解即为最小二乘解
基于半外部和外部精度的参数解均可表示为
若自适应因子αk由方差分量确定，则为半外部精度自适应调节因子，即 式中，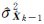
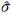和k2分别为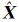k－1和Lk的方差分量估计值，由式(5)计算。
若由外部精度计算自适应因子αk，即
式中，c一般取为1.0～2.0。 式中，|Δ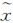
k|为tk历元之前的参数估计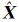k－1与由外部观测信息Lk独立求得的状态参数估计向量
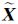k之差。由外部精度求自适应因子的式(10)和式(11)易见，自适应因子αk自适应地平衡当前历元观测信息Lk和tk历元之前的参数估计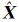k－1对模型参数估计的影响。如此确定的自适应因子比tk历元之前的参数估计获得的方差更能反映模型参数的可靠性。于是，基于式(10)和式(11)确定的自适应因子相对于tk历元之前的参数估计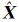k－1和动力学模型而言，属于外部自适应因子。
同样，自适应拟合推估也采用外部观测信息调整事先拟合的协方差函数[19, 20]，使其拟合推估值更接近实际观测。因为原理与自适应滤波相近，这里不再赘述。
4 计算与比较以一实测GNSS网为例，该网包含9个点，其中1号点为起算点。对这一观测网进行两个时段观测，一个时段采用GPS接收机进行观测，另一个时段采用BDS接收机进行观测，每个时段都获得72个基线向量，全部为非同步观测。两个时段的基线解算都具有较高的精度，整体平差后两组观测向量的平均残差都约为0.005 m，原始观测向量中不含粗差。为说明文中各参数估计类的平差解算效果，分别应用内部精度自适应参数估计类中的最小二乘估计，半外部精度自适应参数估计类中的抗差估计和Helmert型方差分量估计，以及外部精度自适应估计类中的自适应序贯平差进行平差解算。
4.1 最小二乘估计与抗差估计选用第一时段观测数据，随机选取6个基线向量加入0.2 m或0.3 m的粗差，然后进行整体最小二乘估计和抗差估计。在抗差估计中，选取的等价权函数为IGGⅢ。表 1列出了加入粗差后最小二乘估计和抗差估计与加入粗差前的最小二乘平差的坐标差比较。
| 加入粗差后的最小二乘估计与加入粗差前的最小二乘估计的坐标差RMS值 | 加入粗差后的抗差估计与加入粗差前的最小二乘估计的坐标差RMS值 | |||||
| RMS_X | RMS_Y | RMS_Z | RMS_X | RMS_Y | RMS_Z | |
| 0.010 0 | 0.014 6 | 0.009 6 | 0.000 4 | 0.000 4 | 0.000 4 | |
经计算，加入粗差后，应用抗差估计的验后单位权中误差与最小二乘平差的单位权中误差的数值之比约为1∶7.6。最小二乘平差后参数平均中误差为0.018 8 m，应用抗差估计后参数平均中误差为0.002 4 m。说明基于半外部精度的参数自适应估计一般优于基于内部精度的参数自适应估计(即最小二乘估计)。
4.2 最小二乘估计与方差分量估计选用两时段观测数据，形成两组观测量。对第2组数据进行处理，加入0.02 m的方差使整组精度降低。处理后第1组数据与第2组数据单独经最小二乘平差得到的单位权中误差之比约为1∶3.4。进行整体最小二乘估计和Helmert型方差分量估计，表 2列出了分别应用最小二乘估计和Helmert型方差分量估计平差后的坐标差比较。
| 加入误差后的最小二乘估计与加入粗差前的最小二乘估计坐标差RMS值 | 加入误差后的Helmert估计与加入粗差前的Helmert估计坐标差RMS值 | |||||
| RMS_X | RMS_Y | RMS_Z | RMS_X | RMS_Y | RMS_Z | |
| 0.003 0 | 0.007 8 | 0.005 3 | 0.000 1 | 0.000 3 | 0.000 1 | |
从计算结果中可得，第2组数据精度降低后，最小二乘平差参数平均中误差为0.004 9 m，应用Helmert型方差分量估计参数平均中误差为0.002 4 m。
4.3 自适应序贯平差以第1组数据为先验信息，第2组数据为当前观测信息，模拟一组动态观测。分别对第1组和第2组观测量单独进行最小二乘平差，第2组的平差结果精度略高于第1组，第2组与第1组的验后单位权中误差之比约为1∶1.2。利用两组平差结果的差值，按照式(10)和式(11)调整参数先验信息的权，再将第2组观测量加入进行自适应序贯平差。表 3列出了自适应序贯平差结果的对比情况。
| 第1组数据加入粗差后与加入粗差前自适应序贯平差坐标差RMS值 | 两组数据都加入粗差后与加入粗差前自适应序贯平差坐标差RMS值 | 加入粗差并进行抗差估计后与加入粗差前自适应序贯平差坐标差RMS值 | ||||||||
| RMS_X | RMS_Y | RMS_Z | RMS_X | RMS_Y | RMS_Z | RMS_X | RMS_Y | RMS_Z | ||
| 0.000 0 | 0.000 0 | 0.000 0 | 0.014 3 | 0.016 5 | 0.012 0 | 0.000 2 | 0.000 3 | 0.000 2 | ||
经计算，自适应序贯平差后的单位权中误差与整体最小二乘平差后的单位权中误差之比约为1∶1.4；在第1组观测量中加入粗差后的结果作为参数先验信息，即先验信息存在异常误差，再进行自适应序贯平差，得到的坐标值几乎没有变化；在第2组观测量中加入粗差后，进行自适应序贯平差，得到的坐标值有明显变化，存在约0.001 m至0.03 m的偏差，单位权中误差增大了约8倍，但进行抗差自适应序贯平差后，获得的结果与参考结果在毫米量级上无差异，说明基于外部精度的自适应估计具有较好的随机模型精度识别能力和调整能力。
5 结 论(1) 基于内部精度参数估计类，如最小二乘估计，适用于观测验前统计模型可靠的情况。若验前随机模型存在异常，仍只用内部精度来确定观测信息的权，会造成观测权分配不合理，导致平差结果出现偏差。
(2) 基于半外部精度的参数自适应估计，如抗差估计和基于方差分量估计的参数自适应估计，具有较好的调节误差影响的能力，因为观测量的权不仅由其方差确定，也由当前观测与其他观测的偏差进行自适应调整，便于控制部分异常误差对模型参数估计的影响。
(3) 基于外部精度的自适应参数估计，如自适应Kalman滤波、自适应序贯平差等，由于随机量的随机模型是由随机量与外部参考信息之差确定的，于是更客观地反映相应观测的偏差，由此确定随机模型也更能控制相应误差的影响。
(4) 必须指出，如果方差-协方差分量估计采用条件闭合差进行解算，则基于方差分量估计的自适应参数估计也应归入外部精度自适应估计类；如果自适应Kalman滤波或自适应序贯平差、自适应拟合推估等，采用半外部精度统计量，则该类自适应估计也变为半外部自适应参数估计类。
| [1] | KOCH K R. Least Squares Adjustment and Collocation [J]. Bulletin Géodésique, 1977, 51(2): 127-135. |
| [2] | MORITZ H. Statistical Foundations of Collocation [J]. Boll Geod Sci Aff, 1980, 2: 131-150. |
| [3] | KOCH K R. Bayesian Inference for Variance Components [J]. Manuscripta Geodaetica, 1987, 12(4): 309-313. |
| [4] | KOCH K R. Maximum Likelihood Estimate of Variance Components [J]. Journal of Geodesy, 1986, 60(4): 329-338. |
| [5] | KOCH K R, KUSCHE J. Regularization of Geopotential Determination from Satellite Data by Variance Components[J]. Journal of Geodesy, 2002, 76(5): 259-268. |
| [6] | OU Z. Estimation of Variance and Covariance Components [J]. Bulletin Géodésique, 1989, 63(2): 139-148. |
| [7] | LI B, SHEN Y, LOU L. Efficient Estimation of Variance and Covariance Components: A Case Study for GPS Stochastic Model Evaluation [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 203-210. |
| [8] | SHEN Yunzhong, LIU Dajie. Unbiased Estimation Formula of Unit Weight Mean Square Error in Regularization Solution [J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 604-610.(沈云中, 刘大杰. 正则化解的单位权方差无偏估计公式[J]. 武汉大学学报: 信息科学版, 2002, 27(6): 604-610.) |
| [9] | XU P, SHEN Y, FUKUDA Y, et al. Variance Component Estimation in Linear Inverse Ill-Posed Models [J]. Journal of Geodesy, 2006, 80(2): 69-81. |
| [10] | TEUNISSEN P J G, AMIRI-SIMKOOEI A R. Least-Squares Variance Component Estimation [J]. Journal of Geodesy, 2008, 82(2): 65-82. |
| [11] | YANG Y, XU T, SONG L. Robust Estimation of Variance Components with Application in Global Positioning System Network Adjustment [J]. Journal of Surveying Engineering, 2005, 131(4): 107-112. |
| [12] | YANG Y. Robust Bayesian Estimation [J]. Bulletin Géodésique, 1991, 65(3): 145-150. |
| [13] | YANG Y. Robust Estimation for Dependent Observations [J]. Manuscripta Geodaetica, 1994, 19(1): 10-17. |
| [14] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights [J]. Journal of Geodesy, 2002, 76(6-7): 353-358. |
| [15] | YANG Y X, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning [J]. Journal of Geodesy, 2001, 75(2-3): 109-116. |
| [16] | YANG Yuanxi, HE Haibo, XU Tianhe. On Adaptively Kinematic Filtering [J]. Acta Geodetica et Cartographica Sinica, 2001, 30(4): 293-298.(杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293-298.) |
| [17] | YANG Yuanxi, ZENG Anmin. Adaptive Filtering for Deformation Parameter Estimation in Consideration of Geometrical Measurements and Geophysical Models [J]. Science in China Series D: Earth Sciences, 2009, 39(4): 437-442.(杨元喜, 曾安敏. 顾及几何观测信息和地球物理模型的形变参数自适应滤波解[J]. 中国科学: D 辑, 2009,39(4): 437-442.) |
| [18] | YANG Y, ZHANG X, XU J. Adaptively Constrained Kalman Filtering for Navigation Applications [J]. Survey Review, 2011, 43(322): 370-381. |
| [19] | YANG Y, ZENG A, ZHANG J. Adaptive Collocation with Application in Height System Transformation [J]. Journal of Geodesy, 2009, 83(5): 403-410. |
| [20] | YANG Yuanxi, ZENG Anmin, WU Fumei. Horizontal Crustal Movement in China Fitted by Adaptive Collocation with Embedded Euler Vector [J]. Science China Earth Sciences, 2011, 41(8): 1116-1125.(杨元喜, 曾安敏, 吴富梅. 基于欧拉矢量的中国大陆地壳水平运动自适应拟合推估模型[J]. 中国科学: 地球科学, 2011, 41(8): 1116-1125.) |
| [21] | SUI Lifen, LIU Yanyu, WANG Wei. Adaptive Sequential Adjustment and Its Application [J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 51-54, 6.(隋立芬, 刘雁雨, 王威. 自适应序贯平差及其应用[J]. 武汉大学学报: 信息科学版, 2007, 32(1): 51-54, 6.) |
| [22] | GRAFAREND E, KLEUSBERG A, SCHAFFRIN B. An Introduction to the Variance-Covariance Component Estimation of Helmert Type [J]. Zeitschrift für Vermessungswesen, 1980, 105(4): 161-180. |
| [23] | LI Bofeng, SHEN Yunzhong, LOU Lizhi. Variance Covariance Component Estimation Based on the Equivalent Residuals[J]. Acta Geodaeatica et Cartogrphica Sinica, 2010, 39(4): 349-354.(李博峰, 沈云中, 楼立志. 基于等效残差的方差-协方差分量估计[J]. 测绘学报, 2010, 39(4): 349-354.) |