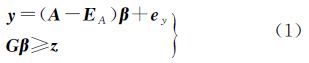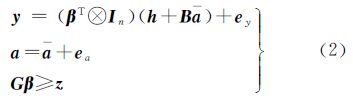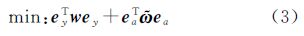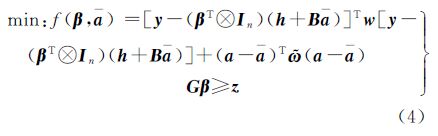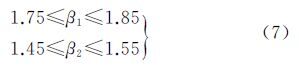2. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079
2. Research Center of GNSS, Wuhan University, Wuhan 430079, China
整体最小二乘估计(total least squares,TLS)作为EIV[1](errors-in-variables)模型的严密估计方法,目前已广泛应用于大地测量等众多科学研究和工程应用领域。文献[2]提出了整体最小二乘准则。文献[3]基于正交回归原理推导了TLS数值算法。假定观测值不相关情况下,文献[4]首次提出了真正统计意义上的TLS算法。文献[5]提出了著名的奇异值分解(singular value decomposition,SVD)算法。文献[6]研究了稳健整体最小二乘算法(robust TLS)等。文献[7]证明了当观测数趋于无穷大时,TLS估计具有渐进无偏性。大地测量领域针对普遍存在的观测值不等精度、相关的情况,文献[8—11]提出了加权TLS算法(weighted TLS,WTLS),其中,文献[11]研究了最一般性权矩阵条件下的WTLS算法。文献[1]提出了基于partial EIV模型(PEIV)的WTLS算法,能够将结构性等各种形式的系数矩阵纳入统一的模型形式求解。其他TLS算法的发展情况见文献[12]。
当参数估计存在先验信息时,EIV模型扩展为附有约束的EIV模型。相当多的文献研究了附有等式约束的EIV模型(equality-constrained EIV,ECEIV),如文献[13]、文献[14]以及文献[15]分别提出了3种不同的附有等式约束的TLS算法(equality-constrained TLS,ECTLS)。
某些先验信息要求对模型附加不等式约束条件,就形成了附有不等式约束的EIV模型(inequality-constrained EIV,ICEIV),如变形监测中某因素引起的变形系数理论上要大于某一数值,应对该估计值进行最小值约束;坐标转换模型的TLS算法中要求强制附合到某中心点,即该点坐标的改正数不能超出一定数值范围等。关于附有不等式约束的EIV模型目前仅检索到两篇研究文献,文献[16]运用拉格朗日乘数法将ICTLS问题转化为广义线性互补问题(linear complementarity problem,LCP),再通过排列组合的方法进行求解。文献[17]提出了基于穷举法的附有不等式约束的整体最小二乘算法(inequality-constrained TLS,ICTLS)。上述文献开启了ICTLS算法研究的先河,但存在以下问题有待解决:①算法的计算量随约束方程个数的增长呈指数增长,如当约束方程个数为50时,组合或搜索次数达到约250≈1015,因此,约束方程较多时,算法的计算量急剧增长甚至导致无法计算;②算法仅适用于系数矩阵元素全部为随机元素的EIV模型以及等精度、不相关观测值。
本文以partial EIV模型为基础,研究了附有不等式约束的加权整体最小二乘(inequality-constrained weighted TLS,ICWTLS)算法。本文提出的ICWTLS算法适用于随机和非随机元素并存、或呈现结构性特征的一般性系数矩阵以及不等精度、相关观测值,并且算法的计算效率远高于基于穷举法的ICTLS算法,计算量不受约束方程个数的制约。
2 附有不等式约束的partial-EIV模型 式中,y表示n×1的观测向量;ey表示y的n×1随机误差向量,且ey期望为0、协因数阵Qy=w-1σ2(w和σ2分别表示观测向量的权阵以及单位权方差);β表示t×1的参数向量;A表示n×t的系数矩阵;EA表示A的n×t随机误差矩阵,EA的期望为0且协因数阵为QA=ω-1σ2(ω表示系数矩阵观测元素的权阵),通常假定EA与ey不相关;G表示不等式约束方程的k×t系数矩阵;z表示k×1的常数向量。现有ICTLS算法[16, 17]假定式(1)中观测数据的权阵ω和w均为单位阵,并且A中元素全部为随机量。当A中存在非随机的固定元素或者呈现结构性特征时,必须对系数矩阵的协因数阵[18]或者对系数矩阵[15]进行特殊处理后求解。为了得到一般性系数矩阵下的统一算法,以partial EIV模型[1]为基础,将传统的ICEIV模型(1)改写为如下形式
式中,仅将A中的随机量提取出来构成m×1估计量a参与平差计算,a表示相应于a的观测向量,ea表示a的m×1随机误差向量;(h+Ba)=vec(A-EA),vec为向量化符号,表示将n×t矩阵(A-EA)按列顺序排列为nt×1的列向量;h为nt×1列向量,对应于vec(A-EA)中的非随机项,其中随机项部分取0,Ba对应于vec(A-EA)中的随机项,B是由常数构成的nt×m矩阵。式(2)构成了附有不等式约束的partial EIV模型(inequality-constvained partial EIV,ICPEIV),与传统的ICEIV模型[16, 17]比较,其优势主要体现为:①将ICEIV模型中系数矩阵元素全部为随机量的限定扩展到了同时包含随机和非随机元素的一般情况;②ICPEIV模型可解析结构性系数矩阵,保证了算法的统一性;③ICPEIV模型A中参与平差计算的待估量个数m小于等于ICEIV中A中元素个数nt,尤其当系数矩阵中的随机量个数较少时,ICPEIV模型形式可以大大减少待估计量。因此,ICPEIV模型更具一般性,以下在不限定观测数据权阵的等精度和相关性的一般情况下,即ICPEIV模型(2)中权矩阵ω和w为任意正定对称阵,笔者提出了普遍适用的附有不等式约束的加权整体最小二乘新算法。
3 (ICWTLS)算法非线性ICPEIV模型(2)的待估参数为β和a,根据整体最小二乘准则
可以求出其最优估计值。由式(2)可得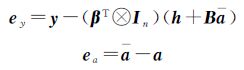
将ey和ea代入式(3),则ICPEIV模型(2)的ICWTLS算法转化为以下附有不等式约束的最优化问题
通过将ICPEIV模型的估计转换为附有不等式约束的最优化问题,避免了现有算法采用穷举法引起的算法受限于不等式方程个数的缺陷。根据最优化理论,提出了基于罚函数法[19]的ICWTLS新算法。
罚函数法的基本思想是通过对目标函数式(4)中的f(βa,)增加一个二次型惩罚项,将式(4)转化为无约束条件的目标函数形式
式中,μ表示惩罚参数(μ>0);ci(β)=max[0,-Giβ+zi](i=1,2,…,k);Gi为G的第i行;zi为z的第i个元素。式(5)存在一阶导数且一阶导数连续。
当式(5)中的二次型惩罚项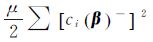 为不等于0的正数时,参数解在可行解范围之外;当惩罚项等于0时,表明参数解必定落在满足式(4)的可行解区域范围内。当惩罚参数μ增大并趋于无穷时,表示在目标函数中加大了约束条件控制程度。因此,从较小的μk值(k=1,2,…,n)开始并逐步增大其数值,将式(5)对待估参数β和a分别求一阶偏导并令其等于0,从而构成方程组或者采用牛顿法等无约束最优化方法均可求得模型的估计值
为不等于0的正数时,参数解在可行解范围之外;当惩罚项等于0时,表明参数解必定落在满足式(4)的可行解区域范围内。当惩罚参数μ增大并趋于无穷时,表示在目标函数中加大了约束条件控制程度。因此,从较小的μk值(k=1,2,…,n)开始并逐步增大其数值,将式(5)对待估参数β和a分别求一阶偏导并令其等于0,从而构成方程组或者采用牛顿法等无约束最优化方法均可求得模型的估计值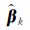 和
和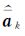 ,其中对应于最小的fICWTLS的参数解
,其中对应于最小的fICWTLS的参数解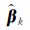 和
和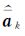 即为ICPEIV模型的最优解。
即为ICPEIV模型的最优解。
基于罚函数法的ICWTLS算法计算过程如下。
(1) 给定初始值:μ0>0及τ>0,β0和0(可采用不考虑不等式约束方程情况下的式(1)的TLS解作为初始值)。
(2) 固定μ0值,根据式(5)估计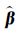 和
和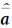 ,直到参数前后两次估计值小于设定的τ。
,直到参数前后两次估计值小于设定的τ。
(3) 如果参数解满足收敛条件,结束计算,转至步骤(4)。
(4) 按给定规则增大μ0,转至步骤(2)进行迭代计算。
(5) 系列μ值下,最小fICWTLS值对应的参数解即为最优估计值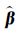 和
和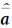 。
。
对于ICPEIV模型估计转换后的最优化式(4),除上述基于罚函数的ICWTLS算法外,同样可以采用最优估计理论的有效集法、序列二次规划法、内点算法等[19, 20]得到相应的ICWTLS算法。基于上述不同最优估计方法的ICWTLS算法的特点是下一步要讨论的问题。
4 实例分析为了说明本文提出的附有不等式约束的整体最小二乘算法的应用,笔者共模拟两个实例进行了计算。实例1的主要目的是验证和比较ICWTLS新算法与现有基于穷举法的ICTLS算法[17]的优缺点及计算效率,因此,笔者设计了一组观测数据等精度并且系数矩阵全部为随机元素的ICEIV模型数据。实例2选择了附有不等式约束的平面拟合模型,该模型的系数矩阵同时存在随机和非随机元素,现有算法无法解算,通过模拟一组不等精度的试验数据,采用ICWTLS算法求出了模型的参数解。
4.1 实例1(等精度、系数矩阵为随机元素)
实例1的模拟数据见表 1,模型包含7×1待估参数向量β以及70×1待估系数向量a,系数矩阵A的全部元素为随机量,A和y中所有观测元素不相关且中误差均为0.1,其中参数真值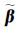 见表 2。为了改进模型的估计结果,利用参数的先验信息设计了18个不等式约束方程(见表 1),其中,0≤βi≤0.8(i=1,2,3,4)以及-0.5≤βj≤0(j=5,6,7)可分别表示为
见表 2。为了改进模型的估计结果,利用参数的先验信息设计了18个不等式约束方程(见表 1),其中,0≤βi≤0.8(i=1,2,3,4)以及-0.5≤βj≤0(j=5,6,7)可分别表示为
(I3⊗[-1, 1]T)β≥([1,1,1]T⊗[-0.5,0]T)
| A | y | ||||||
| -0.841 7 | -5.006 6 | 0.874 6 | -1.010 7 | 0.954 8 | 4.982 7 | -4.972 4 | -2.967 4 |
| -2.024 9 | -3.025 6 | 1.682 7 | -2.571 3 | 2.078 3 | 6.761 6 | -3.754 0 | -4.084 9 |
| -2.870 6 | -0.959 5 | 2.453 9 | -3.846 0 | 3.123 7 | 8.486 4 | -2.621 8 | -4.897 2 |
| -3.963 8 | 1.035 2 | 3.275 6 | -5.090 9 | 4.107 7 | 9.958 3 | -1.320 4 | -5.617 9 |
| -5.026 3 | 3.080 8 | 4.184 5 | -6.616 4 | 4.996 5 | 11.820 0 | -0.351 8 | -6.405 0 |
| -5.891 8 | 4.974 4 | 4.838 5 | -8.006 7 | 5.949 6 | 13.519 6 | 0.892 5 | -7.291 5 |
| -6.901 8 | 7.071 5 | 6.024 6 | -9.500 2 | 6.877 6 | 15.184 9 | 1.892 8 | -7.999 7 |
| -8.011 1 | 9.104 9 | 6.673 9 | -10.855 6 | 8.011 9 | 16.989 3 | 3.452 1 | -8.952 5 |
| -8.870 4 | 11.017 8 | 7.193 2 | -12.335 2 | 9.095 9 | 18.563 6 | 4.500 9 | -9.895 1 |
| -9.821 9 | 13.015 3 | 8.084 5 | -13.563 6 | 9.965 9 | 20.217 4 | 5.774 7 | -10.776 2 |
| G | z | ||||||
| 1.253 | -0.378 | 0 | 2.784 | 0 | -4.201 | 0.541 | 3.510 0 |
| 0 | 3.251 | -0.236 | 0 | 1.526 | -0.693 | 0 | 0.970 0 |
| -2.543 | 0 | 1.487 | 0 | 0.325 | -0.987 | 0 | 1.130 0 |
| 3.458 | 0 | -0.145 | 2.124 | 0 | -1.256 | 3.142 | 1.620 0 |
| 0≤βi≤0.8 (i=1,2,3,4) -0.5≤βj≤0 (j=5,6,7) | |||||||
ICWTLS算法估计值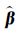 ICWTLS以及基于穷举法的ICTLS算法估计值
ICWTLS以及基于穷举法的ICTLS算法估计值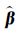 ICTLS见表 2,表中同时计算了不考虑约束方程时的TLS解
ICTLS见表 2,表中同时计算了不考虑约束方程时的TLS解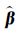 TLS,可以看到:
TLS,可以看到:
| 参数 | 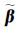 | 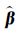 ICWTLS ICWTLS | 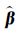 TLS TLS | 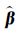 ICTLS ICTLS
|
| β1 | 0.200 0 | 0.152 6 | -0.616 6 | 0.152 6 |
| β2 | 0.300 0 | 0.260 0 | 0.664 6 | 0.260 0 |
| β3 | 0.800 0 | 0.696 1 | -0.451 3 | 0.696 1 |
| β4 | 0.500 0 | 0.504 2 | 0.453 0 | 0.504 2 |
| β5 | -0.100 0 | -0.032 8 | -1.452 6 | -0.032 8 |
| β6 | -0.500 0 | -0.500 0 | 0.047 1 | -0.500 0 |
| β7 | -0.200 0 | -0.160 9 | -0.360 1 | -0.160 9 |
(1) 由于模型数据等精度、系数矩阵全部为随机量,因此,采用本文算法求得的参数解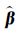 ICWTLS和基于穷举法的参数解
ICWTLS和基于穷举法的参数解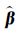 ICTLS相同,均满足全部不等式约束条件
ICTLS相同,均满足全部不等式约束条件
G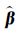 ICWTLS-z=[0.088 4 0.911 6 0.404 8 0.595 2 0.975 3 0.024 7 1.0 0 0.936 5 0.063 5 0.661 4 0.338 6 0.772 9 0.227 1 0 0 0.137 3 0]T≥0
ICWTLS-z=[0.088 4 0.911 6 0.404 8 0.595 2 0.975 3 0.024 7 1.0 0 0.936 5 0.063 5 0.661 4 0.338 6 0.772 9 0.227 1 0 0 0.137 3 0]T≥0
(2) 从算法的计算量比较,本文算法只需迭代计算23次,而穷举法理论上排列组合所需计算次数为218≈260 000。当模型约束方程个数较多的情况下,基于穷举法的ICTLS算法计算量要远大于本文提出的ICWTLS算法。当不等式约束方程过多时,基于穷举法的算法甚至无法在有效时间内求解。
(3) 若不顾及约束条件,采用TLS算法得到的参数解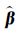 TLS代入不等式约束方程的结果向量如下,其中第1、3、14、15、16、18个元素均小于0,不满足不等式约束条件式
TLS代入不等式约束方程的结果向量如下,其中第1、3、14、15、16、18个元素均小于0,不满足不等式约束条件式
G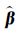 TLS-z=[-0.385 8 1.385 8 -0.039 0 1.039 0 0.970 7 0.029 3 0.714 1 0.285 9 0.733 1 0.266 9 0.491 4 0.508 6 1.103 7
TLS-z=[-0.385 8 1.385 8 -0.039 0 1.039 0 0.970 7 0.029 3 0.714 1 0.285 9 0.733 1 0.266 9 0.491 4 0.508 6 1.103 7
-0.103 7 -0.329 3 -1.634 5 1.437 9 -0.993 4]T
(4) 由于不等式约束条件利用了参数的先验信息,因此本实例的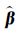 ICWTLS显然比
ICWTLS显然比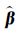 TLS更接近于参数真值
TLS更接近于参数真值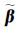 ,即,当平差模型存在可靠的参数的先验信息时,如参数在确定范围内取值、数字地形拟合模型边界范围的设定等,平差算法若能将这些先验信息作为约束条件加入计算过程中,可以有效改善模型的估计结果或者使得估计结果能够满足模型设定的条件。
,即,当平差模型存在可靠的参数的先验信息时,如参数在确定范围内取值、数字地形拟合模型边界范围的设定等,平差算法若能将这些先验信息作为约束条件加入计算过程中,可以有效改善模型的估计结果或者使得估计结果能够满足模型设定的条件。
表 2中,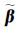 表示参数真值;
表示参数真值;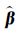 ICWTLS
ICWTLS
表示采用本文ICWTLS算法的参数估计值;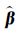 TLS表示不考虑不等式约束方程的TLS算法的参数估计值;
TLS表示不考虑不等式约束方程的TLS算法的参数估计值;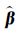 ICTLS表示采用基于穷举法的ICTLS算法的参数估计值。
ICTLS表示采用基于穷举法的ICTLS算法的参数估计值。
线性回归模型是测绘领域常用的基本EIV模型之一,实例2选用平面拟合模型说明ICWTLS算法的应用,平面拟合模型式(1)中观测向量、系数矩阵、参数向量等形式如下

由上式可以看到平面拟合模型的系数矩阵同时包含了非随机和随机元素,即第1列元素为已知量,第2列和第3列是由观测数据构成的随机量,现有附有不等式约束的整体最小二乘算法无法处理这类情况。本文算法可以解算任意结构性系数矩阵形式的EIV模型,将上式表示为partial EIV模型式(2)的形式,式中的矩阵和向量可表示为
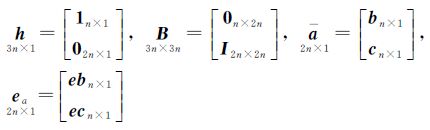
假定根据先验信息,要求模型的截距参数β1和斜率参数β2必须在如下数值范围内
式(7)相当于对平面拟合模型附加了4个参数β的不等式约束方程,相应的G和z见表 3。笔者共模拟了10个拟合点数据,系数矩阵随机量和观测向量的中误差见对应观测数据括号内数值。估计结果见表 4,可以看到,ICWTLS算法参数结果均满足所有不等式约束条件(式(7)),而TLS解并不满足不等式约束方程。即当平差模型存在可靠的先验信息时,将其作为附加约束条件,可得到满足设定条件的估计结果。| 点号 | A | y | G | z |
| 1 | 1 | 1.407(0.3) | 6.700(0.3) | -9.930(0.3) | 1 | 0 | 0 | 1.750 0 |
| 2 | 1 | 2.404(0.3) | 7.058(0.3) | -10.769(0.3) | -1 | 0 | 0 | -1.850 0 |
| 3 | 1 | 2.610(0.3) | 7.947(0.3) | -11.487(0.3) | 0 | 1 | 0 | 1.450 0 |
| 4 | 1 | 4.817(0.5) | 8.993(0.5) | -11.190(0.5) | 0 | -1 | 0 | -1.550 0 |
| 5 | 1 | 5.334(0.5) | 9.691(0.5) | -12.312(0.5) | ||||
| 6 | 1 | 6.115(0.5) | 12.046(0.5) | -13.356(0.5) | ||||
| 7 | 1 | 6.886(0.5) | 12.322(0.5) | -13.239(0.5) | ||||
| 8 | 1 | 7.317(0.7) | 13.053(0.7) | -14.783(0.7) | ||||
| 9 | 1 | 9.067(0.7) | 14.794(0.7) | -15.295(0.7) | ||||
| 10 | 1 | 9.818(0.7) | 14.977(0.7) | -17.204(0.7) |
| 参数 | β1 | β2 | β3 |
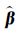 ICWTLS ICWTLS | 1.750 | 1.550 | -2.170 |
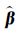 TLS TLS | 4.418 | 2.168 | -2.708 |
当EIV模型存在参数的先验信息时,如模型某些参数取值应在一定范围内或者地形拟合的边界条件等就构成了EIV模型的不等式约束条件。若平差计算顾及到约束条件,可以充分利用模型的先验信息改善估计结果或者使得估计结果满足设定的条件。目前仅有文献[16—17]对ICTLS进行了研究,但提出的算法只适用于系数矩阵全部元素随机、观测数据等权的特殊情况。此外,当约束方程数量较大时,建立在穷举法基础上的ICTLS算法的计算量随约束方程个数呈指数增长;当约束方程数量过大时,算法甚至可能无法在有效时间内进行计算。本文将ICEIV模型改写为更为一般化的ICPEIV模型,并且在整体最小二乘准则下,将模型的求解转化为标准的附有不等式约束的最优化问题,提出的ICWTLS新算法能采用统一的方法估计结构性系数矩阵、随机和非随机元素并存的各种情况,并且没有限制观测数据的精度和相关性。同时,算法的计算量不受约束方程个数的制约。论文通过两个实例对ICWTLS新算法进行了验证和说明,计算结果表明算法较好地解决了现有算法的限制问题,新算法在实际应用中简单、有效、具有普遍适用性。
| [1] | XU P L, LIU J N, SHI C. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675. |
| [2] | ADCOCK R J. Note on the Method of Least Squares[J]. The Analyst, 1877, 4(6): 183-184. |
| [3] | PEARSON K. On Lines and Planes of Closest Fit to Systems of Points in Space[J]. Philosophical Magazine Series 6, 1901, 2(11): 559-572. |
| [4] | DEMING W E. The Application of Least Squares[J]. Philosophical Magazine Series 7, 1931, 11(68): 146-158. |
| [5] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [6] | WASTON G A. Robust Counterparts of Errors-in-variables Problems[J]. Computational Statistics & Data Analysis, 2007, 52(2): 1080-1089. |
| [7] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem: Computational Aspects and Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1991. |
| [8] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [9] | SCHAFFRIN B, LEE I, CHOI Y, et al. Total Least-squares (TLS) for Geodetic Straight-line and Plane Adjustment[J]. Bollettino di Geodesia e Scienze Affini, 2006, 65(3): 141-168. |
| [10] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least Squares Adjustment[J]. Journal of Geodesy, 2010, 85(4): 229-238. |
| [11] | FANG X. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [12] | LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505-512.(刘经南,曾文宪,徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报:信息科学版, 2013, 38(5):505-512.) |
| [13] | SCHAFFRIN B, FELUS Y A. On Total Least-squares Adjustment with Constraints[C]//International Association of Geodesy Symposia. Sapporo: International Association of Geodesy, 2005, 128: 417-421. |
| [14] | MAHBOUB V, SHARIFI M A. On Weighted Total Least Squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3): 607-608. |
| [15] | FANG Xing. A Structured and Constrained Total Least-Squares Solution with Cross-covariances[J]. Studia Geophysica et Geodaetica, 2014, 58 (1): 1-16. |
| [16] | DE MOOR B. Total Linear Least Squares with Inequality Constraints[R]. Delft: Department of Electrical Engineering, 1990. |
| [17] | ZHANG Songlin, TONG Xiaohua, ZHANG Kun. A Solution to EIV Model with Inequality Constraints and Its Geodetic Applications[J]. Journal of Geodesy, 2013, 87(1): 89-99. |
| [18] | MAHBOUB V. On Weighted Total Least-squares for Geodetic Transformation[J]. Journal of Geodesy, 2012, 86(5): 359-367. |
| [19] | NOCEDAL J, WRIGHT S J. Numerical Optimization[M]. New York: Springer, 2006. |
| [20] | FLETCHER R. Practical Methods of Optimization[M]. New York: John Wiley & Sons, 2000. |