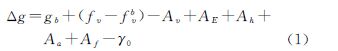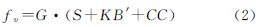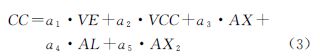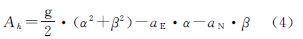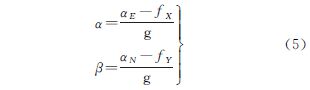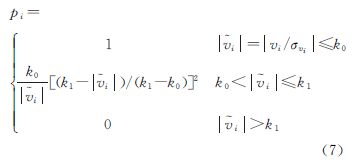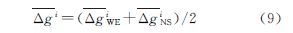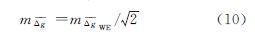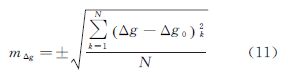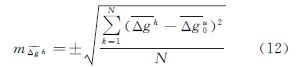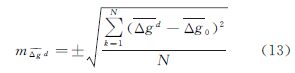2. 地理信息工程国家重点实验室,陕西 西安 710054;
3. 信息工程大学 地理空间信息学院,河南 郑州 450052
2. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China;
3. Institute of Geospatial Information Engineering University,Zhengzhou 450052,China
1 引 言
近20多年来,地球重力场研究在重力测量技术的研发、重力场逼近理论和方法的完善及卫星测高技术的应用3个方面取得了突破性进展。无缝重力由此成为可能。无缝重力一是指全球范围较高分辨率重力测量的无缝覆盖;二是指各类重力测量数据的无缝组合,尤其是陆地和海洋重力数据的无缝组合。我国重力研究离无缝重力的要求相差甚远,除了许多人烟难及的重力空白区外,海岸带重力场的测定和精化也是主要差距之一。
卫星测高技术为开阔海域高分辨率、高精度地球重力场数据的获取提供了强有力的手段,但在海岸带,由于海面状态变化的复杂性以及陆地观测量的匮乏,使卫星测高反演得到的重力场精度急剧下降,从而难以满足海岸带大地水准面精化与其他多种应用的需要。船载重力测量在浅海、滩涂和多岛礁等地区难以实施。航空重力测量成为测定海岸带重力场较为经济和实用的方法。
航空重力测量于20世纪80年代末90年代初试验成功并投入作业[1, 2]。传统的航空重力测量将改进后的船载重力仪(如L&R重力仪)安装在阻尼平台上进行测量,称为阻尼平台式航空重力测量[3],现已成为标准作业方法,对于5~10km的波长分辨率精度为2~8mGal[3, 4, 5, 6]。近些年来,新型航空重力测量系统取得了重大进展(如GT系列重力仪)[7, 8, 9, 10],对于中等分辨率其精度可优于1mGal[10]。航空重力测量已在获取陆海交界等区域的重力场方面发挥出巨大作用[11, 12, 13, 14, 15]。
我国的航空重力测量系统(CHAGS)属阻尼平台式系统,先后于2001年、2002年和2003年进行了3次飞行试验,精度对于5′×5′格网平均重力异常为2~5mGal[6, 16]。为较好地实现陆海重力场以及陆海大地水准面的统一,提高海域大地水准面的精度,我国于2008年开始逐步开展海岸带航空重力测量,本文介绍了CHAGS在渤海湾的测量情况并探讨在区域大地水准面精化中的应用。
2 渤海湾航空重力测量概况渤海湾测区范围共计包含19个1°×1°子块,如图 1所示(为讨论方便,分别表以D1、D2、…、D19)。每个1°×1°子块均布设了南北、东西测线各12条,相邻测线间距为5′。由于测区跨度较大,为提高测量效率,采用4个机场。各机场停机坪的重力基准值(航空重力测量的起始值)按二等重力测量要求从2000重力基本网点联测获得,以保证航空重力与地面重力的基准一致性。
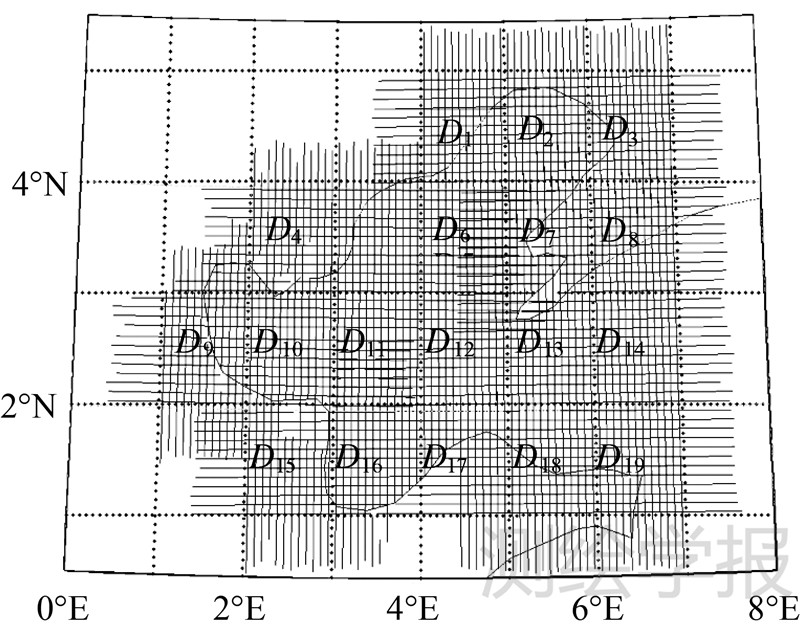
|
| 图 1 渤海湾航空重力测量测线示意图 Fig. 1 Flight lines distribute for Bohai Bay airborne gravimetry |
采用L&R II型航空重力仪,机载动态GPS接收机两套。每架次飞行,测区内均有3个地面GPS基准站,用于差分计算飞机的位置、速度和加速度。所有GPS接收机的采样率均为1Hz。依测区地形,飞行测量期间的平均海拔高约2500m,平均速度约270km/h。测量条件属中等湍流。
3 数据处理要点和精度评估方法 3.1 数据处理要点 3.1.1 数据处理模型 式中,Δg表示测线重力异常;gb系停机坪处的重力值,由陆地重力仪从2000重力基本网点联测得到;fv、fbv表示比力及其初值;Av为飞机的垂直扰动加速度;AE表示厄特弗斯改正;Ah为水平加速度改正;Aa为垂直加速度的姿态改正;Af系空间改正;γ0系正常重力。式(1)右端各项改正的计算方法参见文献[4, 12, 16],本文重点给出易产生系统误差的两项,即fv和Ah。
3.1.2 比力计算比力fv的计算公式为
式中,G为航空重力仪的格值;S为弹簧张力;B′为摆杆速度;K为摆杆尺度因子;CC为交叉耦合改正;VE、VCC、AX、AL、AX2分别是5个交叉耦合监视项的名称,ai(i=1,2,…,5)为其相应的系数。上述G、K和ai等常数是引入系统误差的主要因素[17],由于所用重力仪出厂时间不长,本文未作自行标定,而直接采用厂家给定的数值。
3.1.3 水平加速度改正计算文献[17]研究表明,式(1)中的水平加速度改正Ah是产生系统误差的主要因素。为减弱其影响,本文采用如下模型计算水平加速度改
式中,g为重力加速度,可近似为9.8m/s2;αE、αN分别为利用GPS确定的水平加速度的东、北分量,α、β为相应于αE、αN的重力仪稳定平台的倾角。α、β的计算公式为
式中,fX、fY分别为稳定平台横向水平加速度计和纵向水平加速度计敏感到的水平加速度。式(4)是水平加速度的线性组合,即如果水平加速度是零均值噪声,其产生的水平加速度改正误差的均值也应是零,故在重力估算中不会由此产生系统偏差。实际计算时,由于重力仪稳定平台的倾角在0.01Hz以上的频段基本不含信息[12, 17],因此可采用与平台运动周期相当的60~100s的低通滤波器先对倾角作滤波处理,再用式(4)计算水平加速度改正,以此降低系统偏差的影响。
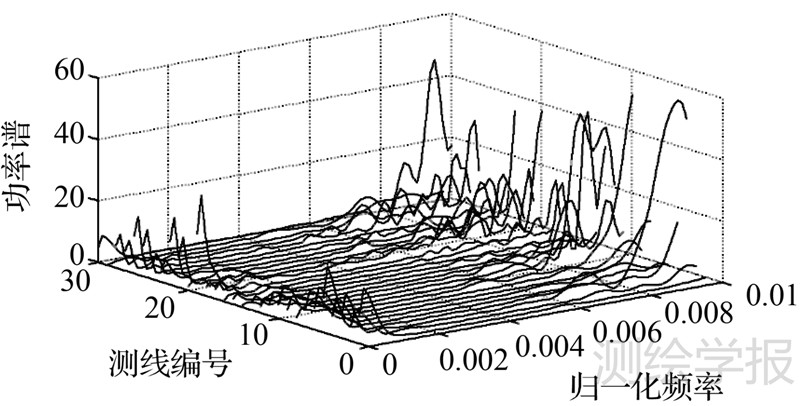
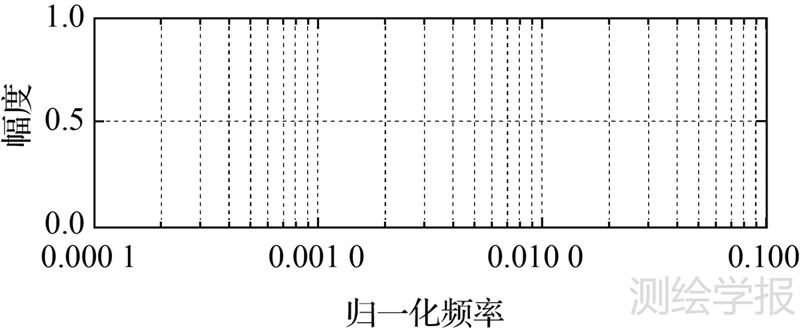
3.1.4 低通滤波器设计式(1)导出的重力异常估值受飞机长周期运动和大气湍流等因素的影响含有大量噪声,低通滤波器的主要作用是减弱高频噪声,有效提取其中的重力信号。滤波器的设计与应用需兼顾空间分辨率和精度要求,短周期滤波器有利于提高空间分辨率,但其不足是残留噪声的增多和精度的降低,反之亦然。本文按照空中原始重力异常的频谱特性(为不失一般性,图 2给出了其中30条测线的原始重力异常的频谱图)和飞机的飞行速度,按5′分辨率要求,设计了截止频率为0.0033Hz的级联式巴特沃思滤波器[16],其相应的时域周期为300s,幅频响应如图 3所示。
|
| 图 2 原始重力异常的功率谱 Fig. 2 PSD of the raw gravity anomaly |
|
| 图 3 低通滤波器的幅频响应 Fig. 3 The amplitude response of filter |
精度评估可采用内符合精度和外符合精度两种评估方法。其中内符合精度本文采用交叉点不符值统计法以及根据测线布设特点引入的重叠格网比较法,外符合精度采用其他已有的重力数据作参考予以比较。
3.2.1 交叉点不符值统计法设第i个交叉点处的重力异常分别为Δgi1、Δgi2,则相应的重力异常不符值为vi=Δgi1-Δgi2,若测线交叉点的个数为N且不符值相互独立,则可按下式估计单个采样点观测值的中误差m
式中,pi是vi相应的权。作等权处理时,式(6)即为单位权中误差。实践中,交叉点不符值中难免存在异常值,一般将不符值的绝对值大于3倍中误差的异常值舍弃后,再统计中误差(以下简称3倍中误差法),或者采用如下加权模型求取抗差估计后的中误差[18]
式中,σvi一般取为vi绝对值的中位数除以0.6745;k0、k1可分别取为1和4。 3.2.2 重叠格网比较法渤海湾航空重力测量,每个1°×1°范围都均匀地布设了12条南北测线和12条东西测线(相邻测线间距为5′),因此,仅用南北测线或东西测线都可构成5′×5′格网平均重力异常,这两者之差在一定程度上反映了航空重力测量的内符合精度,称之为重叠格网比较法。
对于第i个格网,令 为仅由南北测线的观测值所构成的格网平均重力异常,
为仅由南北测线的观测值所构成的格网平均重力异常,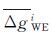 为仅由东西测线的观测值所构成的格网平均重力异常,
为仅由东西测线的观测值所构成的格网平均重力异常,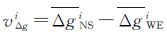 。若格网个数为N,vΔgi之间相互独立且等权,则可按下式估计
。若格网个数为N,vΔgi之间相互独立且等权,则可按下式估计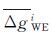 或
或 的中误差m
的中误差m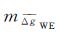
实用中,取第i个格网内的所有观测值(包含南北测线和东西测线)的均值作为该格网的平均重力异常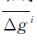 。由于飞行速度较为均匀,同一格网内南北测线和东西测线的观测数相差不大,因此,
。由于飞行速度较为均匀,同一格网内南北测线和东西测线的观测数相差不大,因此,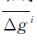 可近似为
可近似为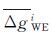 和
和 的平均值,即
的平均值,即
于是,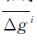 的误差m
的误差m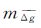 为
为
由此,通过式(8)和式(10)可对航空重力测量的格网平均重力异常的内符合精度作出评估。
3.2.3 外符合精度
设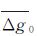 为测区内已有的地面实测格网平均重力异常,将其向上延拓到测线高度可分别求得采样点的重力异常Δg0以及对应的空中格网平均重力异常
为测区内已有的地面实测格网平均重力异常,将其向上延拓到测线高度可分别求得采样点的重力异常Δg0以及对应的空中格网平均重力异常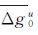 ,以此作为重力参考值,则有如下精度估算公式。
,以此作为重力参考值,则有如下精度估算公式。
采样点上重力异常Δg的中误差按式(11)估算
空中格网平均重力异常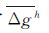 的中误差按式(12)估计
的中误差按式(12)估计
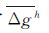 向下延拓得到的格网平均重力异常
向下延拓得到的格网平均重力异常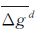 的中误差按式(13)计算
的中误差按式(13)计算
向下延拓属于不适定问题,其精度与测区地形、延拓高度及所用方法等密切相关,通常难以优于2mGal[19, 20, 21, 22, 23],故采用式(13)评估精度时受向下延拓误差的影响较大,较难反映航空重力在飞行面上的测量精度;而向上延拓比较稳定,其精度通常可优于2mGal[19],故本文以式(12)来评价航空重力测量所构成的格网平均重力异常的外符合精度。
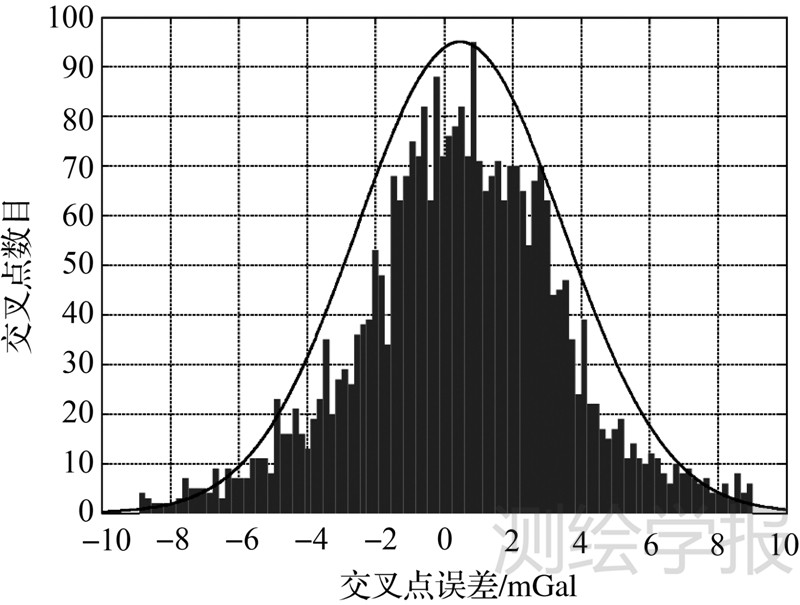
4 渤海湾航空重力测量精度分析 4.1 交叉点不符值统计分析如图 1所示的南北、东西测线总计构成3215个交叉点,其分布位置及交叉点不符值大小示意见图 4(图中,符号○和△分别表示交叉点不符值为非负值和负值,符号大小表示不符值绝对值的大小),图 5是交叉点不符值的直方图,统计结果列于表 1。

|
| 图 4 交叉点不符值示意图 Fig. 4 Sketch of crossover errors |
|
| 图 5 交叉点不符值直方 Fig. 5 Histogram of crossover errors |
| mGal | |||||
| 比较类别 | 均值 | 中误差 | 最小值 | 最大值 | 比较点数 |
| 等权比较 | 0.6 | 4.1 | -59.2 | 76.4 | 3215 |
| 3倍中误差法 | 0.5 | 2.1 | -8.9 | 9.0 | 3021 |
| 抗差估计法 | — | 1.5 | — | — | 3215 |
从图 5可见,交叉点不符值大致服从正态分布,故可以认为不符值之间相互独立。从表 1可以看出,按式(6)利用等权统计、3倍中误差法、抗差估计法的中误差分别为4.1mGal、2.1mGal和1.5mGal。交叉点不符值的均值小于1mGal,表明整体上没有较大的系统性偏差。但从图 4可见,个别测线的系统偏差明显偏大,其主要原因可能是在这些测线的局部位置水平加速度很大,导致水平加速度改正的不完善。
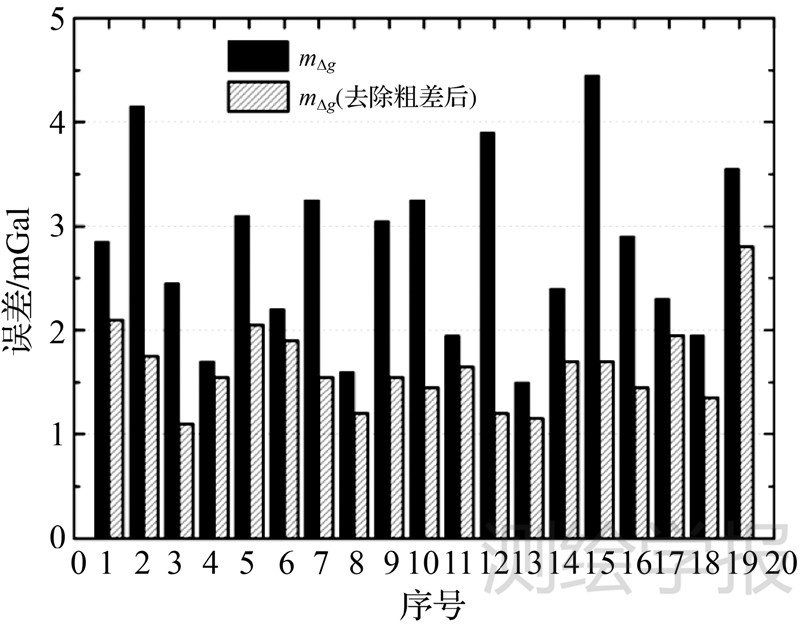
4.2 重叠格网比较结果表 2列出了19个1°×1°分块的重叠格网比较法的相关结果,表中最后一列是按式(10)获得的5′×5′格网平均重力异常的内符合精度,“/”右方数值表示舍掉绝对值大于3倍中误差的差值之后的统计结果。为直观起见,图 6以柱状形式示出了19个1°×1°分块的格网平均重力异常的中误差。
| mGal | ||||||
| 比较项目 | 差值均值 | 标准偏差 | 最小差值 | 最大差值 | 比较点数 | 中误差 |
| D1 | 0.9/0.3 | 5.6/4.2 | -15.5/-11.9 | 25.9/11.9 | 144/137 | 2.8/2.1 |
| D2 | 0.1/-1.1 | 8.3/3.3 | -19.0/-9.3 | 55.4/9.5 | 143/131 | 4.1/1.8 |
| D3 | -0.6/-0.2 | 4.9/2.2 | -36.9/-5.9 | 13.3/6.4 | 144/135 | 2.4/1.1 |
| D4 | -0.1/0.0 | 3.4/3.1 | -12.2/-7.6 | 9.4/9.4 | 144/142 | 1.7/1.5 |
| D5 | -0.0/0.7 | 6.2/4.0 | -25.9/-12.2 | 23.1/12.2 | 142/135 | 3.1/2.0 |
| D6 | 1.4/1.1 | 4.1/3.6 | -7.8/-7.8 | 19.0/9.9 | 143/140 | 2.2/1.9 |
| D7 | 0.3/0.5 | 6.5/3.1 | -25.1/-9.1 | 46.3/8.1 | 143/135 | 3.7/1.6 |
| D8 | -0.0/0.3 | 3.2/2.3 | -19.7/-5.2 | 5.6/5.6 | 144/141 | 1.6/1.2 |
| D9 | 0.4/1.3 | 6.1/2.8 | -48.0/-8.8 | 9.2/9.2 | 144/139 | 3.0/1.5 |
| D10 | 0.5/1.0 | 6.5/2.7 | -34.5/-8.4 | 31.1/7.9 | 144/132 | 3.2/1.5 |
| D11 | 0.4/0.2 | 3.9/3.3 | -11.6/-9.4 | 16.4/9.7 | 144/140 | 1.9/1.5 |
| D12 | 2.2/1.1 | 7.5/2.2 | -5.2/-5.2 | 70.8/6.8 | 144/139 | 3.9/1.2 |
| D13 | 0.4/0.4 | 2.9/2.2 | -16.1/-5.8 | 11.9/6.6 | 144/141 | 3.0/2.3 |
| D14 | 1.8/1.4 | 4.4/3.1 | -11.2/-8.1 | 26.0/10.1 | 144/139 | 2.4/1.7 |
| D15 | -1.6/0.2 | 8.8/3.4 | -56.4/-8.9 | 12.4/8.8 | 140/130 | 4.4/1.7 |
| D16 | 0.6/-0.0 | 5.8/2.9 | -10.3/-7.5 | 32.6/7.4 | 144/138 | 2.9/1.5 |
| D17 | 1.3/1.3 | 4.4/3.7 | -21.4/-9.8 | 19.4/10.7 | 144/142 | 2.3/1.9 |
| D18 | 1.5/0.9 | 3.6/2.6 | -6.4/-6.4 | 21.4/7.9 | 144/137 | 2.0/1.4 |
| D19 | 1.9/1.0 | 6.9/5.5 | -14.7/-14.7 | 27.8/15.6 | 144/139 | 3.5/2.8 |
|
| 图 6 重叠格网法精度统计 Fig. 6 Error histogram for grid-overlapping method |
从表 2及图 6可以看出,对于19个1°×1°分块,重叠格网法中误差的平均值为2.8mGal,若剔除大于3倍中误差的数据,相应的平均值为1.6mGal,该数值和表 1交叉点不符值的抗差估计中误差十分一致。
4.3 与船测重力和卫星测高的比较如图 1的D6、D11分块拥有精度较高、分布均匀的船测重力数据,而D6、D11、D12、D14分块属于宽阔海域,卫星测高重力数据的精度较为可信。以这些数据为参考,可以评估航空重力测量的外符合精度。卫星测高数据采用Sandwell在网上发布的最新数据,该数据的分辨率为2′×2′,比较时将其处理成5′×5′分辨率。船测重力数据同样是5′×5′格网平均重力异常,比较结果统计于<表 3。为直观起见,图 7为D12分块的航空重力与卫星测高的差值,右上为该分块的测线交叉点分布图。图 7中,符号○表示差值为非负,△表示差值为负,○和△的大小反映了差值的相对量级。
| mGal | ||||||
| 比较 项目 | 比较 区域 | 差值 均值 | 标准 偏差 | 均方 根差 | 最小 差值 | 最大 差值 |
| 与船测 比较 | D6 | -2.2 | 2.9 | 3.6 | -7.1 | 18.6 |
| D11 | -1.0 | 2.3 | 2.5 | -5.9 | 8.9 | |
| 与卫星 测高 比较 | D6 | -0.6 | 3.8 | 3.9 | -7.7 | 20.5 |
| D11 | 0.7 | 2.8 | 2.9 | -6.7 | 7.5 | |
| D12 | 0.5 | 4.5 | 4.5 | -7.1 | 27.1 | |
| D12* | -0.1 | 3.2 | 3.2 | -7.1 | 7.8 | |
| D14 | 0.8 | 3.0 | 3.1 | -6.2 | 8.2 | |
从表 3统计结果可以看出,除D12分块,航空重力与船测重力及卫星测高之差的标准偏差均小于4mGal,假设船测重力和卫星测高在该区域的误差分别为1.5mGal和3mGal,则由航空重力获得的5′×5′格网平均重力异常的精度为2~3mGal。在D6分块,航空重力与船测重力、卫星测高的最大差值分别为18.6mGal和20.5mGal,远大于3倍的均方根差;在D12分块,航空重力与卫星测高的最大差值为27.1mGal,6倍于均方根差。从图 7和图 4不难看出,这些异常差值的产生主要归咎于航空重力,因为D6和D12分块中自西向东排列的第8条测线的交叉点不符值普遍较大,说明该条测线的观测质量较差。若舍弃该条测线重新构成D12的格网平均重力异常,其与测高重力之差统计于表 3(示为D12*),显然标准差变小很多(其他测线类似,不再给出)。

|
| 图 7 航空重力与卫星测高之差及交叉点不符值示意图(D12) Fig. 7 Difference between airborne gravity and satellite altimetry and sketch of crossover errors for D12 |
此外,从统计结果还可以看出,航空重力与卫星测高反演结果及船测重力之间尚存在一定系统偏差,但量级不大。一方面,这是由于航空重力数据处理过程中系统性误差未被完全补偿,比如水平加速度改正的不完善及重力仪格值、交叉耦合等引起的误差[16];另一方面可能与卫星测高数据处理中的参考场误差、坐标及重力系统转换误差等有关。此外,所收集到的船测重力已是格网平均重力异常,其是否含有系统误差难以断定。
4.4 与卫星重力的比较为分析航空重力可能存在的长波误差,按D1—D19分块分别由5′×5′格网平均重力异常取平均构成1°×1°格网平均重力异常,再与对应分辨率的模型重力异常进行比较,比较结果列于表 4。此处,选择GOCE重力卫星获得的250阶次的GO-CONS-TIM模型、2190阶次的EGM2008模型和360阶次的DQM2006模型,计算时模型阶次均取至180,以与1°格网分辨率相对应。
| mGal | |||||
| 所用模型 | 差值均值 | 标准偏差 | 均方根差 | 最小差值 | 最大差值 |
| GOCE | -0.15 | 2.68 | 2.69 | -4.73 | 3.84 |
| EGM2008 | -0.81 | 3.83 | 3.92 | -8.38 | 6.49 |
| DQM2006 | 0.02 | 3.40 | 3.40 | -6.68 | 6.24 |
从表 4可见,由航空重力测量获得的1°×1°格网平均重力异常与模型重力异常之间的系统性差异并不显著,与纯卫星模型的系统性差异小于0.5mGal。
5 航空重力在海域大地水准面精化中的应用航空重力数据在海岸带的重要应用之一是实现陆海大地水准面的统一及精化海域大地水准面。为验证航空重力在精化区域大地水准面中的作用,在航空重力测量区域选择了16个GPS/水准点(见图 8),分别用DQM2006、EGM96、EGM2008计算模型大地水准面,然后利用EGM2008模型结合航空重力数据计算重力大地水准面,其与GPS/水准点高程异常的差值统计于表 5。

|
| 图 8 测区GPS/水准点分布示意图 Fig. 8 Distribution sketch of the GPS-leveling points in the test area |
| m | |||||
| 计算方法 | 差值 均值 | 最小 差值 | 最大 差值 | 标准 偏差 | 均方 根差 |
| DQM2006 | 0.17 | -0.05 | 0.48 | 0.17 | 0.28 |
| EGM96 | 0.26 | -0.97 | 1.10 | 0.48 | 0.55 |
| EGM2008 | 0.15 | -0.25 | 0.43 | 0.19 | 0.23 |
| EGM2008+ 航空重力 | -0.02 | -0.16 | 0.26 | 0.12 | 0.12 |
从表 5可以看出,利用模型计算该区域的大地水准面即使是最好的EGM2008,其精度低于20cm。当采用航空重力数据后,精度提高到12cm。因此,航空重力数据可以显著改善海岸带区域的大地水准面精度。
6 结 论航空重力测量业已成为获取海岸带重力场的主要方法,其在陆海重力数据融合及陆海大地水准面统一方面有着重要作用。本文概述了渤海湾地区的航空重力测量情况,给出航空重力测量的主要精度评估方法,针对同一1°×1°测区范围内南北测线和东西测线的相邻测线间距、布设数量大致相同的特点,引入重叠格网比较法以评估格网平均重力异常的内符合精度。通过航空重力与卫星测高、船测重力和卫星重力数据的比较分析以及在精化海域大地水准面中的应用效果分析,初步得出如下结论:
(1) 测线交叉点重力异常不符值的中误差为4.1mGal,抗差估计后的中误差为1.5mGal。受限于实际飞行条件,交叉点处重力异常的不符值难免存在异常值,因此直接由交叉点不符值估算的内符合精度往往难以真实反映格网平均重力异常的精度,根据交叉点不符值大小赋以不同的权即进行抗差估计后,其精度估计更为合理。
(2) 重叠格网比较法所获得的精度估计与格网平均重力异常的外符合精度非常吻合,也与交叉点不符值的抗差估计结果相一致,实践中可择情采用。
(3) 与船测、卫星测高反演获得的重力异常相比,5′×5′格网平均重力异常之差的标准偏差分别为2.3mGal和2.7mGal,扣除船测、卫星测高的误差,由航空重力测量获得的5′×5′格网平均重力异常的精度可优于2.0mGal。
(4) 由航空重力测量获得的1°×1°格网平均重力异常与GOCE卫星重力位模型的计算值相比较,其系统性差异小于0.5mGal,中误差约为2.7mGal,表明航空重力数据与卫星重力之间不存在明显的系统性差异。
(5) 利用EGM2008模型结合航空重力数据计算的大地水准面与16个GPS水准点的比较精度约为12cm,比单独利用EGM2008模型的计算精度提高了近1倍,表明航空重力数据可以显著改善海岸带区域大地水准面的精度。
| [1] | BROZENA J M, CHILDERS V A. The NRL Airborne Geophysics Program [C]//Proceedings of IAG Geodesy beyond 2000——The Challenges of the First Decade. Berlin:Springer Verlag, 2000: 126-130. |
| [2] | VALLIANT H D. The LaCoste and Romberg Air/Sea Gravity Meter: An Overview [M]. Boca Raton:CRC Press, 1991. |
| [3] | VERDUN J,BAYER R, KLINGELE E, et al. Airborne Gravity Measurements over Mountainous Areas by Using a LaCoste&Romberg Air-sea Gravity Meter [J]. Geophysics, 2002, 67(3): 807-816. |
| [4] | KLINGELE E E,COCARD M, HALLIDAY M E, et al. The Airborne Gravimetric Survey of Switzerland [R]. Zürich:Swiss Geophysical Commission,1995. |
| [5] | FORSBERG R, OLESEN A V. Airborne Gravity Survey of Sea Areas around Greenland and Svalbard 1999-2001 [M]. Copenhagen: National Survey and Cadastre, 2003. |
| [6] | XIA Zheren, SHI Pan, SUN Zhongmiao, et al. Chinese Airborne Gravimetry System CHAGS [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 216-220.(夏哲仁,石磐,孙中苗,等. 航空重力测量系统CHAGS[J]. 测绘学报,2004, 33(3):216-220.) |
| [7] | ARGYLE M, FERGUSON S. AIRGrav Results: a Comparison of Airborne Gravity Data with GSC Test Site Data [J]. The Leading Edge, 2000, 10: 1134-1138. |
| [8] | WOOLDRIDGE A. Review of Modern Airborne Gravity Focusing on Results from GT-1A Surveys [J]. First Break, 2010, 28(5): 85-92. |
| [9] | STUDINGER M, BELL R,FREARSON N. Comparison of AIRGrav and GT-1A Airborne Gravimeters for Research Applications [J]. Geophysics, 2008, 73(6): 151-161. |
| [10] | GLENNIE C,SCHWARZ K P, BRUTON A M, et al. Comparison of Stable Platform and Strapdown Airborne Gravity [J]. Journal of Geodesy, 2000, 74(5): 383-389. |
| [11] | HEHL K, BASTOS L,CUNHA S, et al. Concepts and First Results of the AGMASCO Project [C]// Proceedings of International Symposium on Kinematic System in Geodesy, Geomatics and Navigation.Banff:[s.n.], 2001: 557-563. |
| [12] | OLESEN A V. Improved Airborne Scalar Gravimetry for Regional Gravity Field Mapping and Geoid Determination [D]. Copenhagen: University of Copenhagen, 2002. |
| [13] | GUO Zhihong, XIONG Shengqing, ZHOU Jianxin, et al. The Research on Quality Evaluation Method of Test Repeat Lines in Airborne Gravity Survey [J]. Chinese Journal of Geophysics, 2008, 51(5): 1538-1543.(郭志宏,熊盛青,周坚鑫,等. 航空重力重复线测试数据质量评价方法研究[J].地球物理学报,2008, 51(5): 1538-1543.) |
| [14] | FORSBERG R, OLESEN A V. Airborne Gravity and Geoid Surveys in the Arctic and Baltic Seas [C]//Proceedings of IAG International Symposium on Gravity, Geoid and Geodynamics 2001. Banff:[s.n.], 2001: 586-592. |
| [15] | CHEINWAY HWANG, YU-SHEN HSIAO, HSUAN-CHANG SHIH. Data Reduction in Scalar Airborne Gravimetry: Theory, Software and Case Study in Taiwan [J]. Computers and Geosciences, 2006, 32:1573-1584. |
| [16] | SUN Zhongmiao. Theory, Methods and Application of Airborne Gravimetry [D]. Zhengzhou: Information Engineering University , 2004. (孙中苗. 航空重力测量理论、方法及应用研究 [D]. 郑州:信息工程大学,2004.) |
| [17] | SUN Zhongmiao, ZHAI Zhenhe, XIAO Yun, et al. Systematic Error Compensation for Airborne Gravimetry [J]. Chinese Journal of Geophysics , 2013, 56(1): 47-52. (孙中苗,翟振和,肖云,等. 航空重力测量的系统误差补偿[J].地球物理学报,2013, 56(1): 47-52.) |
| [18] | YANG Yuanxi. Robust Estimation for Dependent Observations [J]. Manuscripta Geodaetica, 1994, 19: 10-17. |
| [19] | WANG Xingtao, SHI Pan, XIA Zheren, et al. Comparison of Different Downward Continuation Methods for Airborne Gravity Data [J]. Chinese Journal of Geophysics,2004,47(6):1017-1022.(王兴涛,石磐,夏哲仁,等. 航空重力测量数据向下延拓方法比较[J]. 地球物理学报,2004,47(6):1017-1022.) |
| [20] | GU Yongwei, GUI Qingming. Study of Regularization Based on Signal to Noise Index in Airborne Gravity Downward to the Earth Surface [J]. Acta Geodaetica et Cartographica Sinica, 2010,39(5):458-464. (顾勇为,归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J].测绘学报, 2010,39(5):458-464.) |
| [21] | JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. The Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity [J]. Acta Geodaetica et Cartographica Sinica, 2011,40(6):684-689(蒋涛,李建成,王正涛,等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011,40(6):684-689.) |
| [22] | DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regularization Algorithm in Downward Continuation of Airborne Gravity Aata [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40 (6): 690-696. (邓凯亮,黄谟涛,暴景阳,等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报,2011,40(6): 690-696.) |
| [23] | JIANG Tao, DANG Yamin, ZHANG Chuanyin, et al. Downward Continuation of Airborne Gravity Aata Based on Rectangular Harmonic Analysis [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 475-480.(蒋涛,党亚民,章传银,等. 基于矩谐分析的航空重力向下延拓[J]. 测绘学报, 2013, 42(4): 475-480.) |