高光谱影像虽然有很高的光谱分辨,但是空间分辨率往往较低[1],从而使影像中普遍存在着混合像元,影响影像的分类精度。提高高光谱影像分类精度的主要手段是混合像元分解,混合像元分解的步骤主要包括端元提取和丰度反演[2]。端元提取算法根据光谱数据中是否存在纯净像元分为端元识别算法和端元生成算法[3]。端元识别算法假定影像中存在纯净像元,并直接选取不同纯净像元作为端元;端元生成算法是从影像中产生端元,过程较为复杂。目前常用的端元提取算法主要有纯净像元指数法(pixel purity index,PPI)[4]、内部最大体积法(N-FINDR)[5]、顺序最大凸锥(sequential maximum angle convex cone,SMACC)[6]、顶点成分分析法(vertex component analysis,VCA)[7, 8]、最大体积法(MaxV)、最大距离法(MaxD)、单体增长算法(simplex growing algorithm,SGA)[9]、正交子空间投影算法(orthogonal subspace projection,OSP)[10]等。丰度反演作为像元分解的另一个重要组成部分,其实质就是把影像中每个混合像元含有的端元百分比计算出来。常用的丰度反演方法主要有最小二乘法、滤波向量法、迭代光谱混合分析法、基于端元投影向量的丰度反演方法和基于单形体体积的丰度反演方法等[10]。
本文在对上述端元提取与丰度反演方法研究的基础上,提出基于压缩感知(compressive sensing,CS)理论的端元提取模型,用于实现高光谱影像混合像元组分的有效识别;同时,将经典牛顿力学模型引入到混合像元的丰度反演中,并提出基于万有引力模型(universal gravitation model,UGM)的丰度反演算法。
2 理论与方法 2.1 端元提取模型 2.1.1 CS理论CS是近年来信号处理领域诞生的一种新的信号处理理论[11, 12, 13, 14, 15],该理论自诞生之日起便极大地吸引了相关研究人员的关注。CS突破了奈奎斯特采样定理的限制,能够在几乎不损失原始信号信息量的基础上大量减少采样数据,提高数据处理的运算效率。
任何一个长度为N的一维离散时间信号x都可以看作RN空间N×1的列向量,都可以用一组N×1的规范正交基向量{Ψi}(i=1,2,…,N)线性组合表示。以Ψi为列向量组成N×N的正交基矩阵Ψ,则任意的信号x可以表示为x=Ψs,s为系数矩阵。CS理论认为只要信号x在正交基矩阵Ψ的变换系数s具有稀疏性,就能以较低频率M(M«N)采样信号,并能够以高概率重构该信号。假设x在正交基矩阵Ψ的变换系数是稀疏的,用一个与正交基矩阵Ψ不相关的M×N(M«N)观测基E对系数向量进行线性变换,那么就可以利用优化求解方法从观测集合y(M×1)精确或高概率的重构原始信号x,具体见式(1)
运用CS理论进行信号降维的关键有[16]:①寻找最佳正交基矩阵Ψ,使信号x能够稀疏表示;②设计与Ψ不相关的观测矩阵E(M×N)使得稀疏向量s从N维降到M维时信息不遭破坏;③设计算法使得原始信号x从观测信号y中快速准确重构。一般的自然信号x并不是稀疏的,为此需要找到能够稀疏表示信号的正交基矩阵。目前有很多进行信号稀疏表示的算法,较好的有k均值奇异值分解(k-means singular value decomposition,k-SVD)[17]以及冗余字典下的稀疏分解[18]。在信号重构方面,由于观测数量M远远小于N,方程组y=EΨs看似无解,但是x的稀疏性使问题得到了解决。目前常用的CS重构算法有很多,如正交匹配追踪(orthogonal matching pursuit,OMP)算法[19]、分段OMP(StOMP)算法[20]、基追踪(basis pursuit,BP)算法[12]、树形匹配追踪(tree matching pursuit,TMP)算法[21]、链式追踪(chaining pursuit,CP)算00法。2.1.2 SOFM特征聚类
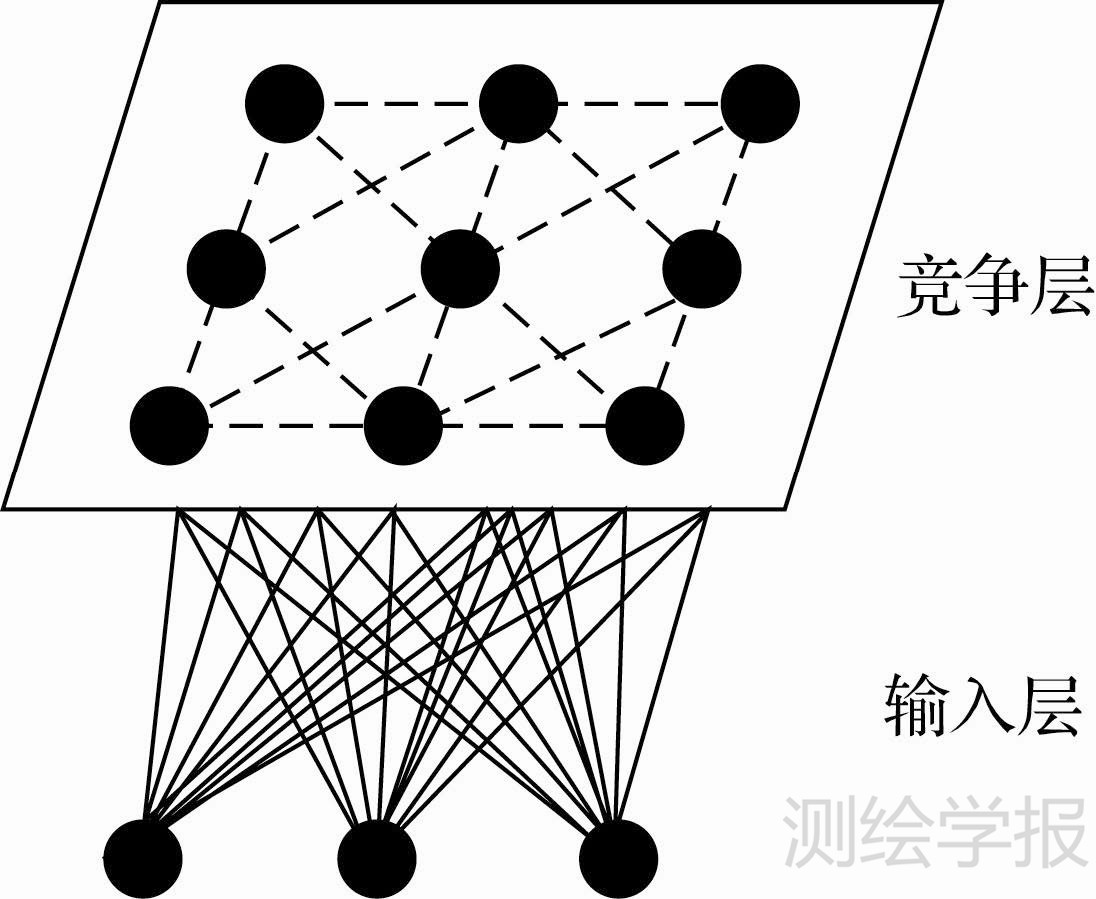
自组织特征映射(self-organizing feature map,SOFM)神经网络由文献[22]提出。该神经网络是一种无导师学习网络,由输入层和竞争层组成,竞争层的各个神经元相互连接,其网络拓扑结构见图 1。
|
| 图 1 SOFM拓扑结构示意图 Fig. 1 The diagram of the SOFM topological structure |
SOFM神经网络不需要训练样本学习,能够根据输入向量的内在特征自组织的学习,将学习结果映射到竞争层来实现分类。
2.1.3 基于CS理论的端元提取模型本文提出的CS端元提取模型的步骤是:①将影像压缩至最佳维度。为使降维后数据丢失信息量尽量少,在降维之前需要对影像进行试验,选取最佳降维维数,将图像压缩至最佳维度。②选取候选端元集。在每一维度上选取一定数量的最大值、最小值,综合各个维度,选取一定数目的候选端元点,组成候选端元集。③端元聚类。将候选端元集在SOFM神经网络中进行聚类,聚类的数目可以参考SMACC算法,从而得到指定个数的分类结果。④端元信号重构。所得的端元还在低维度空间,通过OMP算法,使端元返回至高维度空间,从而得到端元提取结果。具体细节见图 2。

|
| 图 2 基于CS算法端元提取流程 Fig. 2 Flowchart of endmember extracting based on the CS algorithm |
由傅里叶(Fourier)级数分解可知,任何曲线函数f(t)可以分解为无限多个不同频率的正弦和余弦信号的叠加,展开如式(2)所示的傅里叶级数形式
式中,A0/2为谐波余项;Ah和Bh分别为傅里叶谐波系数;L为周期;h为分解次数;t为时间。将光谱曲线的波段总数Z替换周期L,号数s代替t,波段则每条光谱曲线可以按照式(2)进行傅里叶级数分解。曲线分解后决定曲线形状的主要是余弦系数Ah和正弦系数Bh[23],因此可以将光谱曲线分解成正余弦信号的叠加。曲线分解的次数太多会影响算法效率,过少则不可避免地存在较大的信息量损失。通过计算逆变换得到的光谱与原始光谱曲线的均方根误差,可以实现对分解次数分析,均方根误差的计算见式(3)
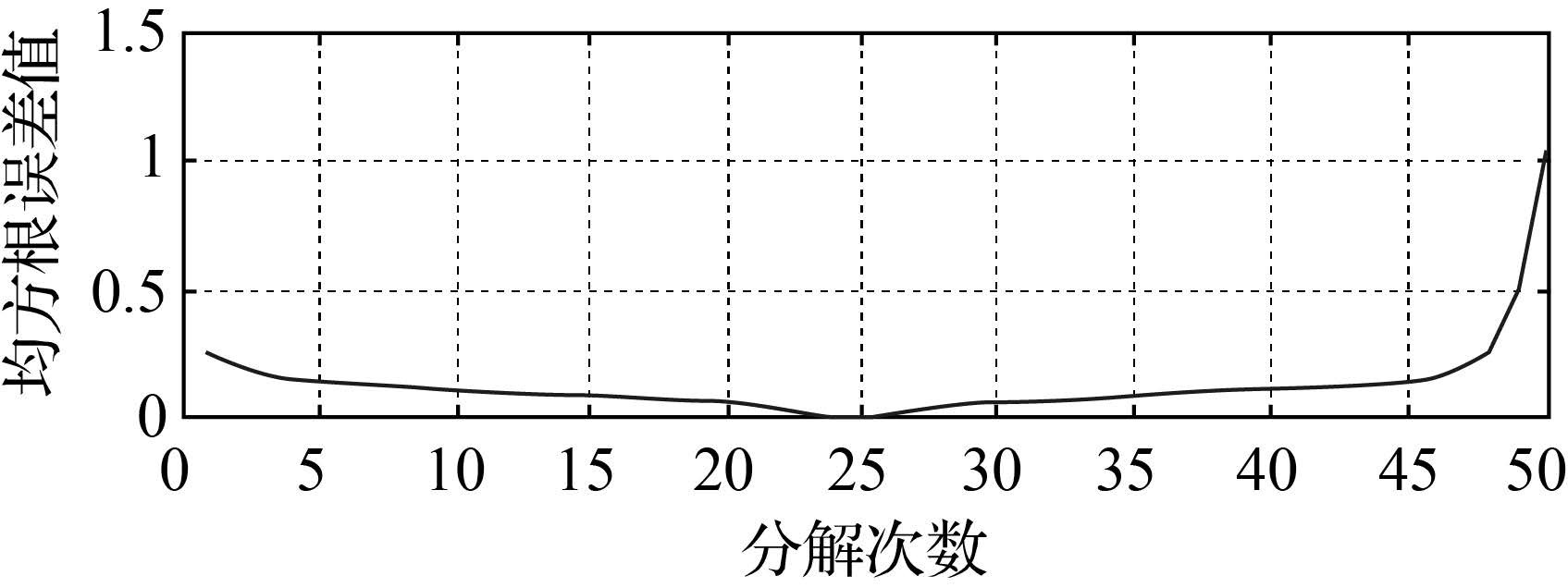
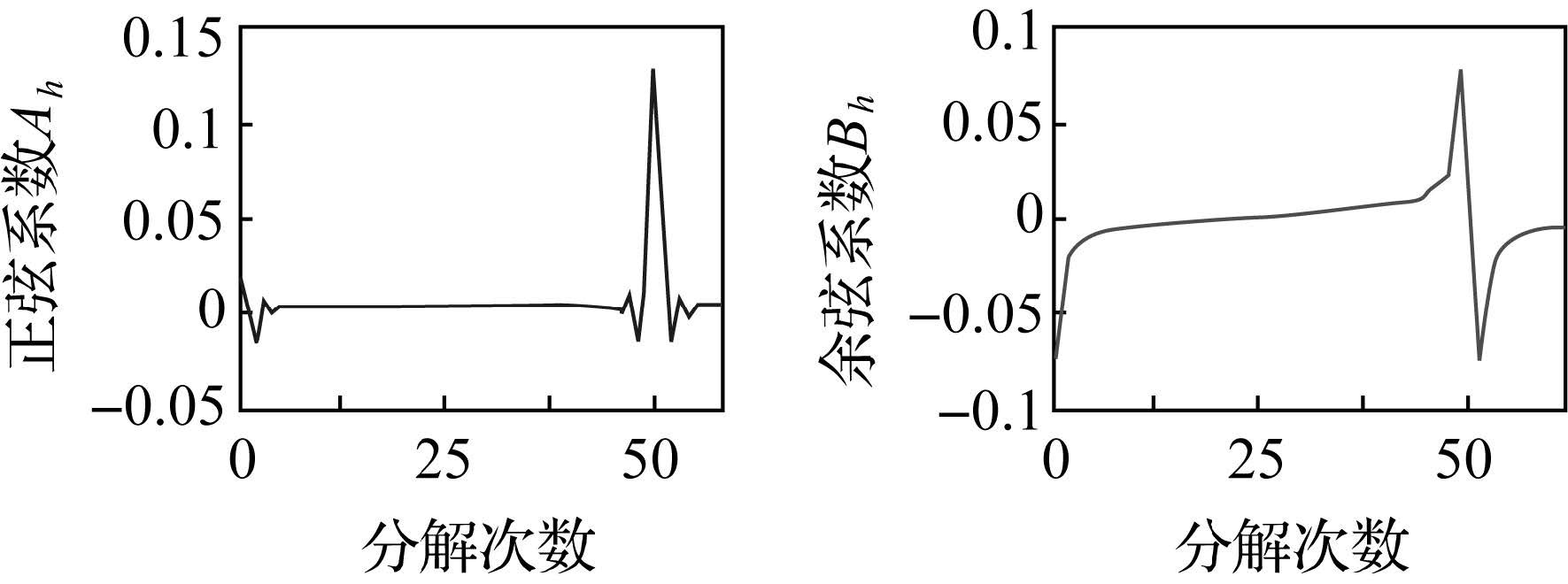
式中,f′(s)为曲线傅里叶级数展开式值;f(s)为曲线函数值。图 3为不同分解次数的整体均方根误差。从图中可以发现均方根误差先减小后增大,当分解次数为波段数的一半时,均方根误差最小。因此,最佳分解次数值可以确定为所研究影像有效波段数的一半。在最佳分解次下对波谱曲线进行分解,正弦系数Ah和余弦系数Bh随着分解次数的变化规律见图 4。以波段的一半作为分解次数进行分解时,随着分解次数的变大,系数接近为0。在顾及精度的同时为了增加算法的效率,将波谱曲线分解次数h定为5。
|
| 图 3 不同分解次数下均方根误差曲线 Fig. 3 RMSE curve under different decomposing times |
|
| 图 4 分解系数随傅里叶分解次数的变化 Fig. 4 Coefficient variation with Fourier decomposing times |
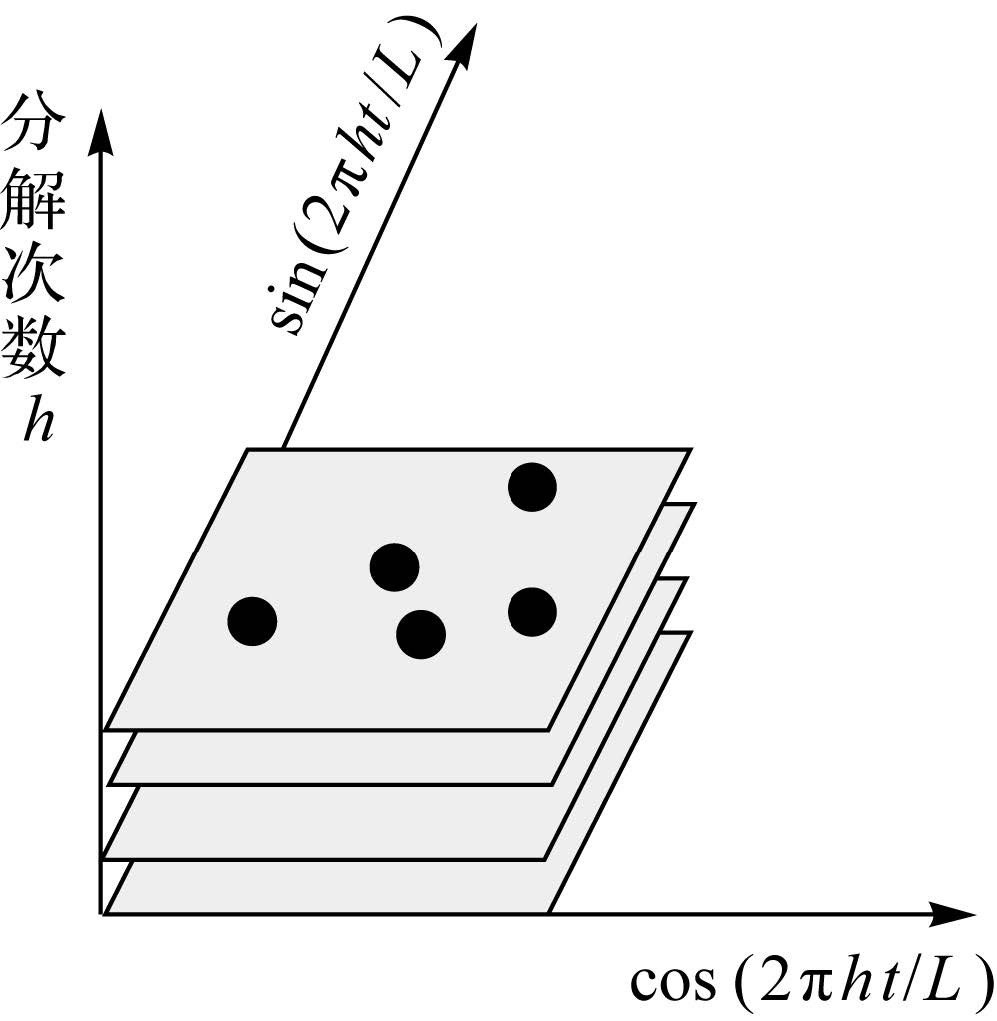
将曲线按(cos(2πht/L),sin(2πht/L))为一组投影基底投影到二维平面上,这样就将曲线转换到二维平面上,如图 5所示。该投影变换将高光谱影像每个像元光谱转换为h个二维平面空间的点,从而将光谱空间转换到二维的平面空间中。
|
| 图 5 混合像元光谱曲线投影示意图 Fig. 5 Spectral projection diagram of the mixed pixels |
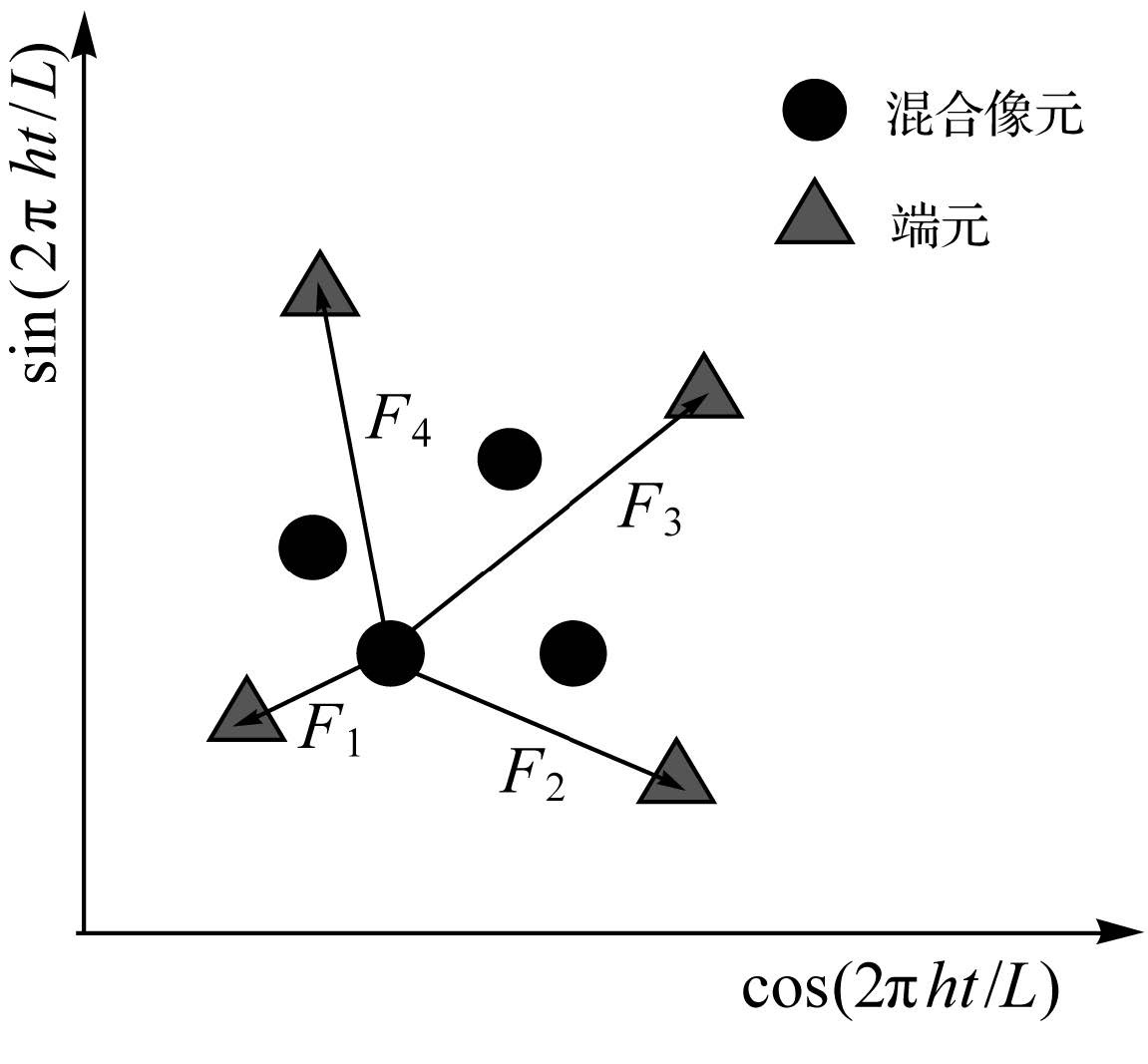
根据光谱空间转换思想以及选定的特定分解次数,将高光谱每个像元光谱以及提取的端元光谱投影变换到二维平面空间中。混合像元和端元的关系可描述为:各个端元与混合像元之间存在牛顿万有引力,混合像元所处的位置不同,受到各个端元对其作用力的大小和方向不同,并在各个力的相互作用下处于平衡状态,如图 6,图中“●”表示混合像元,“▲”表示端元。混合像元的丰度反演可以看成是求取这种平衡状态下,各个端元与混合像元之间万有引力的大小,具体计算见式(4)
式中,n为端元个数;h为曲线分解次数;G为万有引力系数;Fnh为端元n在第h个平面的万有引力;α和β分别为光谱曲线空间变换后的横、纵坐标值;m1和m2代表端元和混合像元的质量(在本次研究中暂不作讨论,将m1和m2统一设为1)。
3 试验与分析 3.1 试验数据试验数据的区域位于云南省香格里拉县城向北70km的格咱乡大山深处,地理坐标为:99°56′00″E—100°02′30″E,27°58′00″N—28°08′00″N,面积约为162km2,如图 7所示。试验数据采用Hyperion高光谱遥感影像,该影像拥有242个波段,光谱分辨率为10nm,空间分辨率为30m,光谱范围355~2577nm,本试验选取了其中较前50个波段,波长范围为426~925nm。
|
| 图 6 丰度反演示意图 Fig. 6 Schematic diagram of the abundance inversion |

|
| 图 7 研究区的Hyperion高光谱影像 Fig. 7 Hyperion hyperspectral image of the study area |
为了验证CS端元提取模型的正确性及可行性,分别用SMACC方法和CS模型进行Hyperion高光谱影像端元提取,通过所提取结果的对比,分析本文所提出CS模型的优势。为了使两种方法提取的端元结果对比更有说服力,端元提取的条件需要进行统一。试验数据都是用研究区域的同一幅原始影像;波谱识别的判断依据统一采用波谱特征拟合(spectral feature fitting,SFF),权重都设为1。
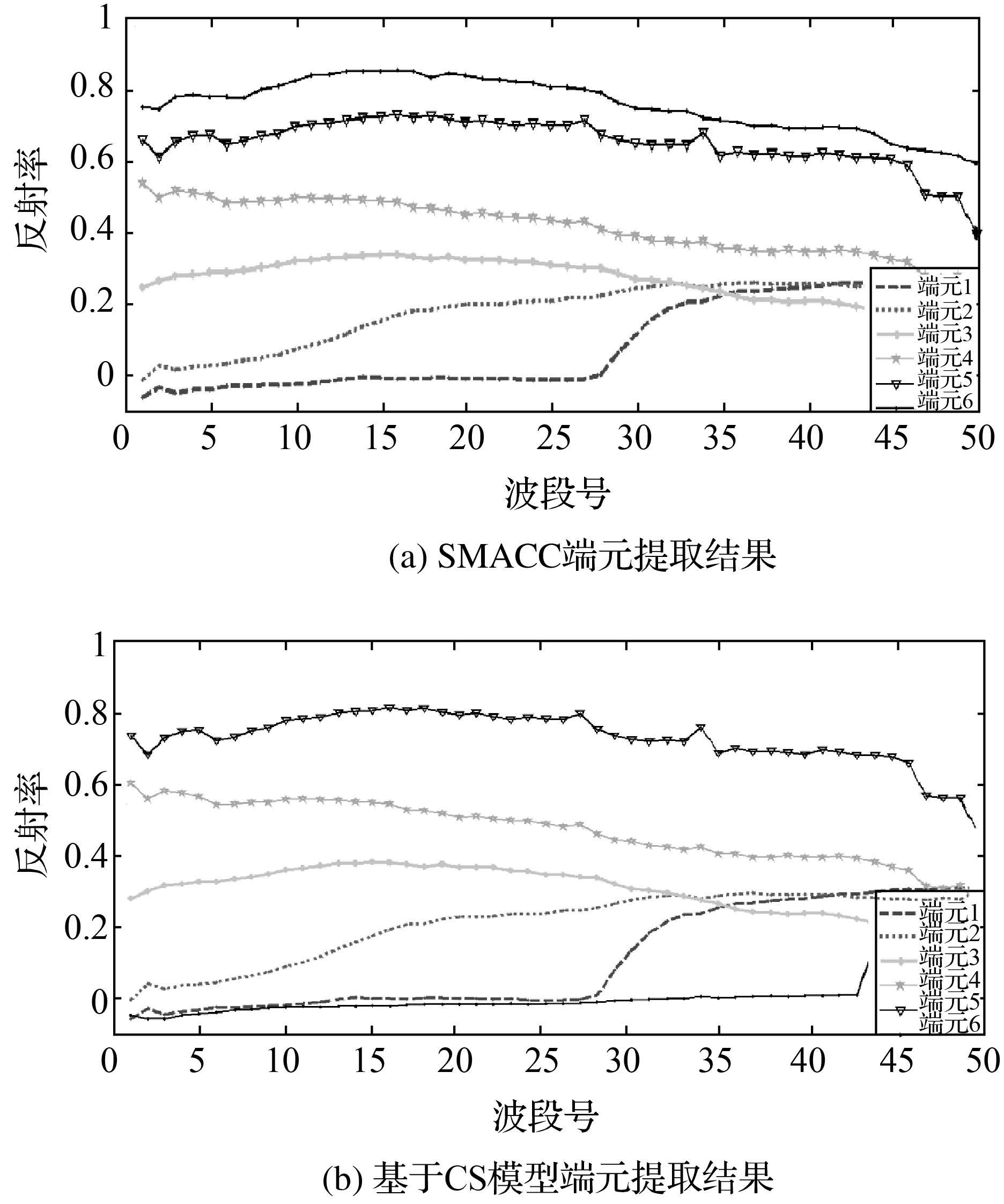
3.2.1 SMACC方法的端元提取结合给定的约束条件得到影像端元,设置端元数目为10,误差容许值为0.01,并根据预定的条件生成了试验数据Hyperion影像的10条端元光谱,进行相似光谱合并后,最终得到6条端元光谱,如图 8(a)所示。将所提取端元波谱与美国地质调查局(United States Geological Survey,USGS)公布的地物光谱库进行SFF的相似度比较,识别出基于SMACC方法提取的端元所代表地物,如表 1所示。
|
| 图 8 两种端元提取结果对比 Fig. 8 Comparison diagram of two endmember extrac-tion results |
| 端元 | 识别结果 | SFF值 |
| 端元1 | Vegetation(植被) | 0.821 |
| 端元2 | Corundum(金刚玉) | 0.466 |
| 端元3 | Muscovite(白云母) | 0.545 |
| 端元4 | Mizzonite(针柱石) | 0.791 |
| 端元5 | Roscoelite(钒云母) | 0.799 |
| 端元6 | A-chloride(卤砂) | 0.803 |
将基于CS理论的端元提取模型在Matlab中编程实现对试验数据Hyperion影像的端元获取,最终也得到6条端元光谱,结果如图 8(b)。同样,将所提取端元波谱与USGS公布的地物光谱库进行SFF的相似度比较,识别出基于CS理论提取的端元所代表地物如表 2所示。
| 端元 | 识别结果 | SFF值 |
| 端元1 | Vegetation(植被) | 0.871 |
| 端元2 | Corundum(金刚玉) | 0.738 |
| 端元3 | Muscovite(白云母) | 0.520 |
| 端元4 | Mizzonite(针柱石) | 0.618 |
| 端元5 | Roscoelite(钒云母) | 0.706 |
| 端元6 | Augite(辉石) | 0.627 |
从试验结果可以看出,SMACC方法提取的端元波谱与CS端元提取模型提取的端元波谱整体上有一定相似性。两种方法提取的端元1—5波形十分一致,而且本文提出的端元提取模型提取了与端元1易区分的端元6,由此可得出基于CS的端元提取模型能够实现更有区分度端元的提取。植被的诊断性光谱带主要位于可见光与近红外,矿类物质的诊断性光谱带主要位于近红外1300~2500nm,本文的试验数据所用的光谱范围更有利于植被端元的识别。最后将两种方法提取植被的端元波谱与USGS公布的数据作比较,SMACC方法的SFF值为0.821,而CS端元提取模型的SFF值为0.871(其值更大),由此可以推断出基于CS理论提取出的端元与USGS光谱库中相应地物光谱具有较高的吻合度。可见,本文提出的基于CS理论端元提取模型取得了较为满意的结果。
3.3基于UGM的丰度反演将研究区光谱曲线数据转换到二维平面特征空间中,然后用式(4)计算基于CS端元提取模型所提取的端元丰度值。其中,植被与金刚玉的端元丰度反演结果如图 9所示。
本文采用均方根误差(RMSE)对丰度反演精度进行评价,通过式(5)计算波段数为n的均方根误差
式中,RMSE为均方根误差;ei为第i波段的误差。得到的RMSE影像如图 10所示。统计RMSE影像数据,结果如表 3所示。由表 3可知丰度反演的RMSE值整体较小,且最大值只有0.5571,因此,本文提出基于UGM的丰度反演算法达到了较高精度水平。
| 评定指数 | 最小值 | 最大值 | 均值 | 标准差 |
| 数值 | 0 | 0.5571 | 0.2563 | 0.0129 |

|
| 图 9 基于UGM的植被与金刚玉端元丰度反演结果 Fig. 9 Inversed abundance results of vegetation and corundum endmembers based on UGM |

|
| 图 10 端元丰度反演的RMSE图像 Fig. 10 RMSE map of endmember abundance inversion |
本文在混合像元的分解中引入了CS理论与UGM,为端元提取与丰度反演作了一些探索性的研究,也为混合像元分解提供了一种思路及参考。本文取得的主要成果有:①结合CS理论和SOFM神经网络技术提出了一种端元提取方法。CS能够在损失很少信息的情况下将高维数据降到低维,减少数据的冗余,提高模型的效率。SOFM神经网络能够自动寻找数据的内在规律进行自动聚类,能够减少人为因素影响,能够提高数据处理的自动化、精确化。②将经典牛顿力学应用到丰度反演中,提出了UGM下的丰度反演算法。基于UGM的丰度反演算法通过转换光谱特征空间,使混合像元投影到二维平面空间中,将丰度反演转换为二维平面的距离问题,使问题变得简单明了、易于实现。
对于结果的可信度及精度,针对端元提取模型和丰度反演算法采用不同的方式进行评价。将基于CS理论的端元提取模型试验结果与SMACC方法提取的端元相比较,并对端元与USGS公布的数据进行识别,证明了本文提出的CS端元提取模型有一定的可行性和较高的可信度。采用RMSE指标对丰度反演结果进行精度评定,得出基于UGM的丰度反演算法满足精度要求。
| [1] | FENG Mingbo, LIU Xue, ZHAO Dong. A Fusion Method of Hyperspectral and Multispectral Images Based on Projection and Wavelet Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2):158-163. (丰明博, 刘学, 赵冬. 多/高光谱遥感图像的投影和小波融合算法[J]. 测绘学报, 2014, 43(2):158-163.) |
| [2] | KESHAVA N, MUSTARD J F. Spectral Unmixing[J]. Signal Processing Magazine, 2002, 19(1): 44-57. |
| [3] | LI Ersen, ZHU Shulong, ZHOU Xiaoming, et al. The Development and Comparison of Endmember Extraction Algorithms Using Hyperspectral Imagery[J]. Journal of Remote Sensing, 2011, 15(4): 659-679. |
| [4] | BOARDMAN J W, KRUSE F A, GREEN R O. Mapping Target Signatures via Partial Unmixing of AVIRIS Data in Summaries[C]//The Fifth JPL Airborne Earth Science Workshop. Pasadena: JPL Publication, 1995: 23-26. |
| [5] | WINTER M E. N-FINDR: An Algorithm for Fast Autonomous Spectral Endmember Determination in Hyperspectral Data[C]//SPIE’s Proceedings of Imaging Spectrometry. Denver:[s.n.], 1999, 3753: 266-275. |
| [6] | GRUNINGER J H, RATKOWSKI A J, HOKE M L. The Sequential Maximum Angle Convex Cone (SMACC) Endmember Model[C]//SPIE Proceedings of Algorithms for Multispectral, Hyperspectral and Ultraspectral Imagery X. Orlando:[s.n.], 2004, 5425: 1-14. |
| [7] | NASCIMENTO J M P, DIAS J M B. Vertex Component Analysis: a Fast Algorithm to Unmix Hyperspectral Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 898-910. |
| [8] | ZHAO Chunhui,WANG Nannan. Anomaly Detection of Hyperspectral Imagery Based on Background Restrain and VCA[J]. Applied Science Technology, 2009, 36(9): 11-14.(赵春晖,王楠楠. 基于背景抑制及顶点成分分析的高光谱异常小目标检测[J]. 应用科技, 2009, 36(9): 11-14.) |
| [9] | CHANG C I, WU C C, LIU W M. A New Growing Method for Simplex-based Endmember Extraction Algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2804-2819. |
| [10] | ZHANG Bing, GAO Lianru. Hyperspectral Image Classification and Target Detection[M]. Beijing: Science Press, 2011: 102-150. (张兵, 高连如. 高光谱图像分类与目标探测[M]. 北京: 科学出版社, 2011: 102-150.) |
| [11] | CANDES E J. Compressive Sampling[C]//Proceedings of the International Congress of Mathematicians. Madrid:[s.n.], 2006: 1433-1452. |
| [12] | CANDES E J, ROMBERG J, TAO T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. |
| [13] | CANDES E J, TAO T. Near Optimal Signal Recovery from Random Projections: Universal Encoding Strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. |
| [14] | DONOHO D L, TSAIG Y. Extensions of Compressed Sensing[J]. Signal Processing, 2006, 86(3): 533-548. |
| [15] | DONOHO D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| [16] | SHI Guangming, LIU Danhua, GAO Dahua, et al. Advances in Theory and Application of Compressed Sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081. (石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081.) |
| [17] | AHARON M, ELAD M, BRUCKSTEIN A M. K-SVD: an Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. |
| [18] | SHEN H F, LI X H, ZHANG L P, et al. Compressed Sensing-based Inpainting of Aqua Moderate Resolution Imaging Spectroradiometer Band 6 Using Adaptive Spectrum-Weighted Sparse Bayesian Dictionary Learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2):894-906. |
| [19] | TROPP J, GILBERT A. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. IEEE Transaction on Information Theory, 2007, 53(12): 4655-4666. |
| [20] | DONOHO D L, TSAIG Y, DRORI I. Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121. |
| [21] | LA C, DO M N. Signal Reconstruction Using Sparse Tree Representations[C]//Proceedings of Society of Photo-Optical Instrumentation Engineers Conference. San Diego:[s.n.],2005: 273-283 |
| [22] | KOHONEN T. Self-organized Formation of Topologically Correct Feature Maps [J]. Biological Cybernetics, 1982, 43(1):59-69. |
| [23] | YANG Keming, ZHANG Tao, WANG Libo, et al. Harmonic Analysis Fusion of Hyperspectral Image and Its Spectral Information Fidelity Evaluation[J]. Spectroscopy and Spectral Analysis, 2013, 33(9): 2496-2501. (杨可明, 张涛, 王立博, 等. 谐波分析法高光谱影像融合及其光谱信息保真度评价[J]. 光谱学与光谱分析, 2013, 33(9): 2496-2501.) |