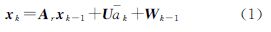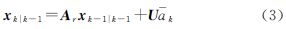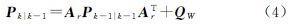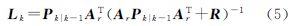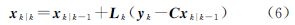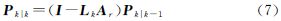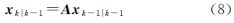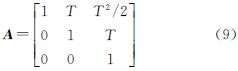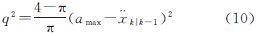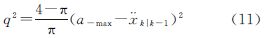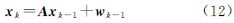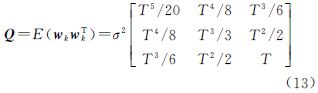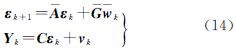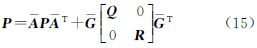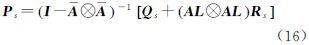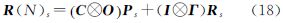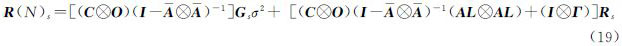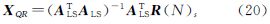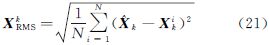2. 武汉大学 地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079;
3. 测绘遥感信息工程国家重点实验室,湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy,Ministry of Education,Wuhan University,Wuhan 430079,China;
3State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan 430079,China
1 引 言
目标跟踪是指人们运用各种观测和计算手段,实现主体对被关注运动客体状态建模、估计和跟踪的过程。伴随着Kalman滤波技术的发展和应用,其在军事领域和民用领域均有着广泛的应用[1, 2]。可靠的Kalman滤波则需要有可靠的函数模型和随机模型[3]。近几十年来,国内外学者对机动载体运动模型问题展开了讨论,建立的模型包括:微分多项式模型、常速度模型、常加速度模型、Singer模型[4]、半马尔柯夫模型[5]及“当前”统计模型等[6, 7, 8]与Jerk模型[9, 10]。当加速度为常数或小范围波动时,通常认为采用常加速度模型建模较为合理,而当加速度同时含有随机机动和确定机动时,则采用“当前”统计模型建模而更为合理[1]。
“当前”统计模型把机动目标加速度的一步预测看作是“当前”统计加速度,同时利用机动加速度方差与状态噪声协方差的关联实现目标的方差自适应滤波[7, 8, 11, 12]。但其中机动频率α的选择仍然是应用此模型的一个难点问题[13, 14, 15]。因此从一个简单的模型出发,合理的调整协方差矩阵,使其能反映载体的机动变化,也将是不错的选择。文献[1]提出了基于常加速度模型的自适应加速度算法,在计算状态噪声协方差时同样采用与“当前”统计模型自适应算法相同计算方法,通过理论分析和仿真试验得出结论:基于常加速度模型的自适应加速度算法与“当前”统计模型的性能基本相当。但需要注意的是,无论是“当前”统计模型自适应算法还是基于常加速度模型的自适应加速度算法均不是真正意义上的自适应,其中最大加速度参数a±max的选取是经验性的,其取值对自适应滤波结果有着直接影响[1]。并且,在进行自适应滤波时仅对状态噪声协方差矩阵进行调整,无法对观测噪声协方差矩阵进行估计。
国内外学者针对自适应Kalman滤波算法展开了广泛研究,提出了极大似然法、贝叶斯法、协方差匹配法、相关法以及自适应抗差Kalman滤波方法[16, 17]。自协方差最小二乘噪声估计方法是基于相关法的一种自适应Kalman滤波方法,且具有较高的噪声估计精度,近年来被广泛应用[18, 19, 20, 21]。本文基于常加速度模型建模的基础上,顾及状态噪声协方差矩阵满足特定结构,提出了一种简化的自协方差噪声估计方法,通过建立Kalman滤波新息与未知状态噪声协方差矩阵和观测噪声协方差矩阵间的函数模型,进而求解未知的噪声协方差矩阵。其目标跟踪精度较“当前”统计模型自适应算法和基于常加速度模型的自适应加速度算法有着明显提高。
2 “当前”统计模型
当加速度不仅包含随机机动,同时包含确定性机动时,一般认为采用有色噪声而不是白噪声描述加速度将更加合理。机动目标跟踪的“当前”统计模型采用非零均值和修正瑞利分布表示机动加速度的特性,本质上是加速度均值非零的一阶时间相关模型。令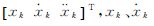 和
和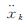 分别表示机动载体的位置、速度和加速度,则其运动状态可表示为
分别表示机动载体的位置、速度和加速度,则其运动状态可表示为
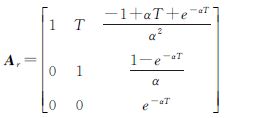
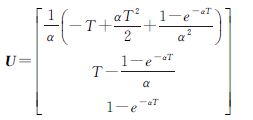
α为相关时间的倒数,即机动频率;T为采样间隔;ak为“当前”加速度的均值;系统状态噪声Wk-1的协方差矩阵
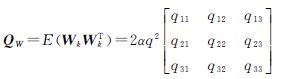
qij(i=1,2,3; j=1,2,3)的具体形式可参考文献[7]。
假设测量方程为
式中,yk为观测值;C为设计矩阵;vk为测量噪声。此时,“当前”统计模型的Kalman滤波的计算如下
式中,Lk表示k时刻的滤波增益矩阵;Pk|k-1表示k时刻的一步预测误差方差矩阵。
把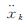 的一步预测值
的一步预测值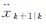 看作(k+1)T瞬间的“当前”加速度即随机加速度的均值,则此时Kalman滤波一步预测可表示为[7]
看作(k+1)T瞬间的“当前”加速度即随机加速度的均值,则此时Kalman滤波一步预测可表示为[7]
式中
采用加速度方差自适应算法时,状态噪声协方差矩阵QW中q2的取值为:
(1) 当“当前”加速度为正时
(2) 当“当前”加速度为负时
式中,amax和a-max分别为相应坐标轴上的加速度上限和下限。
3 简化自协方差最小二乘法尽管“当前”统计模型从形式较常加速度模型更为合理的对机动载体的运动轨迹进行了描述,但其模型相比常加速度模型更加复杂,且其中关键的机动频率α和最大加速度a±max的取值是经验性的,不合适的参数的选择也会使最终的滤波结果退化。
当载体加速度为常数或者处于小范围波动时,可采用常加速度模型对机动载体的运动进行建模,则其运动状态可表示为
式中,wk-1为系统状态噪声,其协方差矩阵为对称非对角矩阵,即
式中,σ2为常量方差。
从式(8)可知,把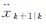 看作加速度的均值时,“当前”统计模型的一步预测实际采用的是常加速度模型的状态矩阵,同时从式(6)可知,k时刻的状态估值xk|k与状态预测值xk|k-1、观测值yk以及滤波增益矩阵Lk,说明“当前”统计模型与常加速模型进行目标跟踪的唯一区别在于滤波增益矩阵Lk的计算。“当前”统计模型中Lk是关于Ar、C、QW和R的函数,而在常加速度模型中Lk是关于A、C、Q和R的函数,如果能合理的调整噪声协方差矩阵,常加速度模型也能体现出和“当前”统计模型相当的目标跟踪效果。
看作加速度的均值时,“当前”统计模型的一步预测实际采用的是常加速度模型的状态矩阵,同时从式(6)可知,k时刻的状态估值xk|k与状态预测值xk|k-1、观测值yk以及滤波增益矩阵Lk,说明“当前”统计模型与常加速模型进行目标跟踪的唯一区别在于滤波增益矩阵Lk的计算。“当前”统计模型中Lk是关于Ar、C、QW和R的函数,而在常加速度模型中Lk是关于A、C、Q和R的函数,如果能合理的调整噪声协方差矩阵,常加速度模型也能体现出和“当前”统计模型相当的目标跟踪效果。
文献[1]提出了基于常加速度模型的自适应加速度算法,其在计算状态噪声协方差时同样采用与“当前”统计模型自适应算法相同的式(10)和式(11)。通过理论分析和仿真试验得出:基于常加速度模型的自适应加速度算法和“当前”统计模型的性能基本相当。但需要注意的是,无论是“当前”统计模型自适应算法还是基于常加速度模型的自适应加速度算法均不是真正意义上的自适应,其中参数a±max的选取也是经验性的,其取值对自适应滤波结果有着直接影响,并且在进行自适应滤波时仅对状态噪声协方差矩阵进行估计,无法对观测噪声协方差矩阵进行估计。
自协方差最小二乘噪声估计方法是基于相关法的一种自适应Kalman滤波方法,且具有较高的噪声估计精度,近年来被广泛应用。采用自协方差最小二乘法进行噪声估计时,是对状态噪声协方差矩阵和观测噪声协方差矩阵中的每一个非零元素进行估计。当采用常加速度模型对机动载体进行建模时,则需对状态噪声协方差矩阵Q中的9个元素进行估计。顾及矩阵Q满足式(13)结构,则Q阵的确定可转变为常数σ2的求解,因此,本文提出一种基于常加速度模型的简化自协方差最小二乘噪声估计方法。
为了方便描述,令

则常加速度模型的状态噪声协方差矩阵Q=σ2G。用L表示稳态的卡尔曼滤波增益,εk表示预测状态向量的误差,令A=(A-ALC)、=[I-AL]、w k=[wkvk]T,新息Yk=yk-Cxk|k-1。构造基于新息的状态空间模型为
预测状态向量协方差P=E(εkεTk),滤波达到稳态时,其满足Lyapunov等式
将式(15)展开,并进行克罗内克积运算,整理可得
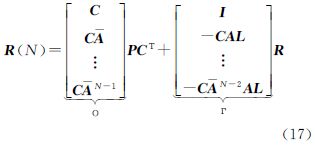
式中,“⊗”表示克罗内克积算子,下标“s”表示矩阵按列序排列。式(16)建立了预测状态向量协方差矢量Ps与状态噪声协方差矢量Qs、观测协方差矢量Rs之间的线性关系。同时令R(N)=[E(YkYTk) … E(Yk+NYTk)]T,由此可得新息{Yk}的相关函数R(N)可表示为
同理,对式(17)进行克罗内克积运算,可整理为
式(18)建立了相关函数R(N)S与预测状态向量协方差矢量Ps、观测协方差矢量R<sub>s之间的线性关系。并将式(16)代入式(18),同时顾及Qs=Gsσ2,整理可得
因为状态噪声协方差矩阵Q满足特殊结构,对Q中各元素的求解转换为常数σ2的确定。通过构造基于新息的状态空间模型,将新息Yk的相关函数R(N)表示为常数σ2和观测协方差矩阵R的函数,由此可同时对σ2、R进行估计,进而确定Kalman滤波模型的噪声协方差矩阵。式(19)可采用最小二乘估计的方法进行求解
式中
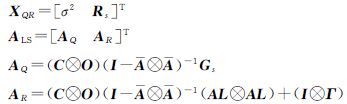
自协方差最小二乘噪声估计方法是直接对状态噪声协方差矩阵和观测噪声协方差矩阵中的非零元素进行估计。当采用常加速度模型对机动载体进行建模时,顾及其状态噪声协方差矩阵满足特定结构,可对自协方差最小二乘估计方法进行简化,将对状态噪声协方差矩阵中各元素的求解转换为对常量方差σ2的求解,提高噪声估计的精度。
本文所提方法无须对机动频率和最大加速度进行先验假设,只需先验设定常量方差和观测噪声协方差,且通过迭代计算后可避免常量方差和观测噪声协方差的初值对目标跟踪精度所带来的误差影响[21]。
4 数值仿真为了验证本文提出的基于常加速度模型的简化自协方差最小二乘噪声估计的Kalman滤波方法(ALSCA)的有效性,通过100次蒙特卡罗仿真来比较自适应“当前”统计模型(ACS)、自适应常加速度模型(ACA)和ALSCA的机动目标跟踪性能。
设置如下两类仿真环境:①阶跃加速度,0~400 s载体以3 m/s的速度做匀速运动,401~500 s以0.5 m/s2的加速度做匀加速运动,501~700 s载体做匀速运动,701~800 s载体以1.5 m/s2的加速度做匀加速运动,801~1000 s载体再做匀速运动;②变加速度,0~200 s载体以-1000 m/s的速度做匀速运动,201~600 s载体以0.09 m/s3的加加速度做变加速运动,601~1000 s载体以-0.09 m/s3的加加速度做变加速运动。直接在真实位置的输出上叠加白噪声信号作为位置的观测值。位置误差的方差取1 m2,采样间隔为1 s。
采用状态估计质量的RMS作为试验结果的评价指标[22],其定义为
式中,N表示蒙特卡罗仿真试验的总次数;i表示第i次仿真;k表示第k个历元。
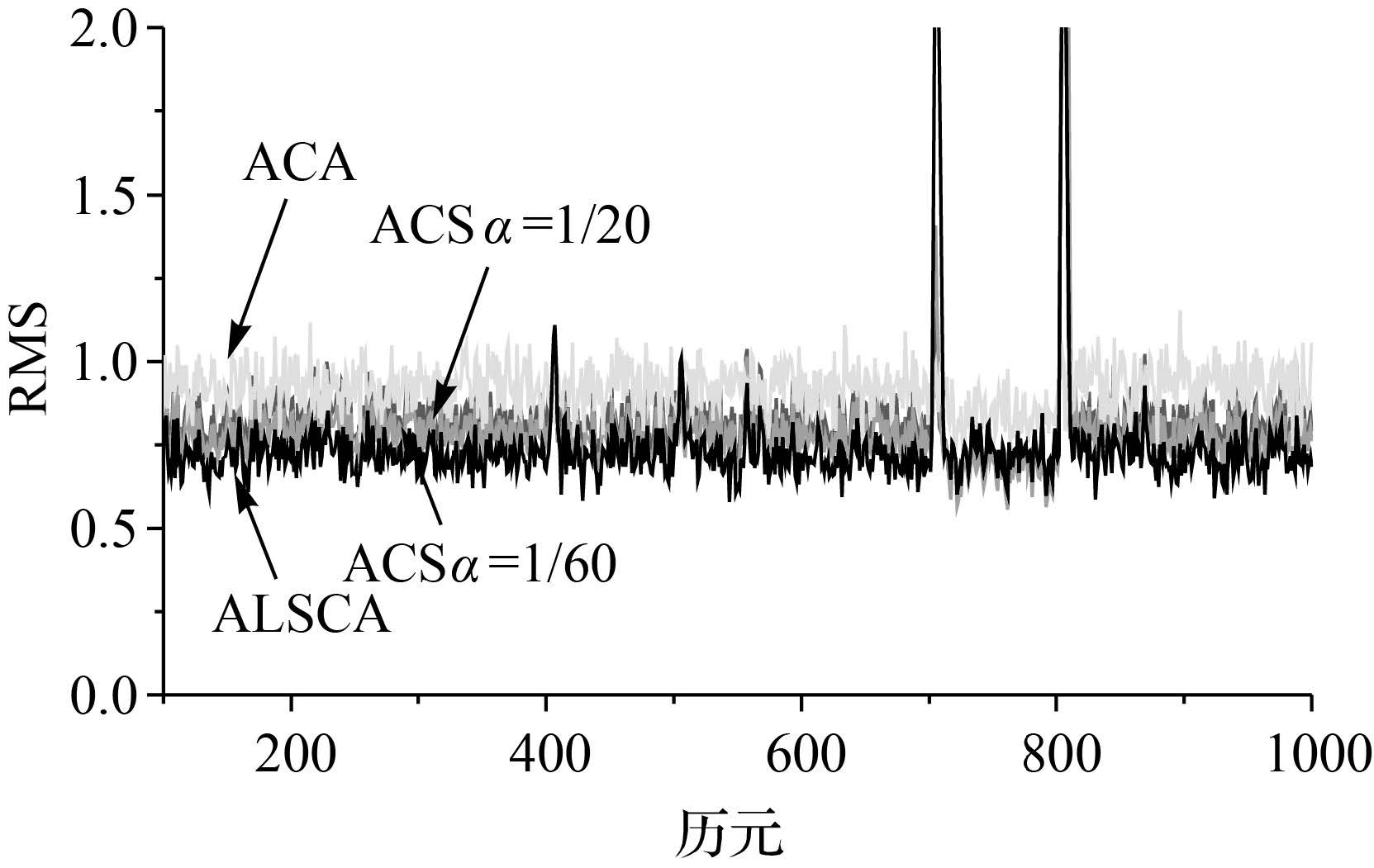
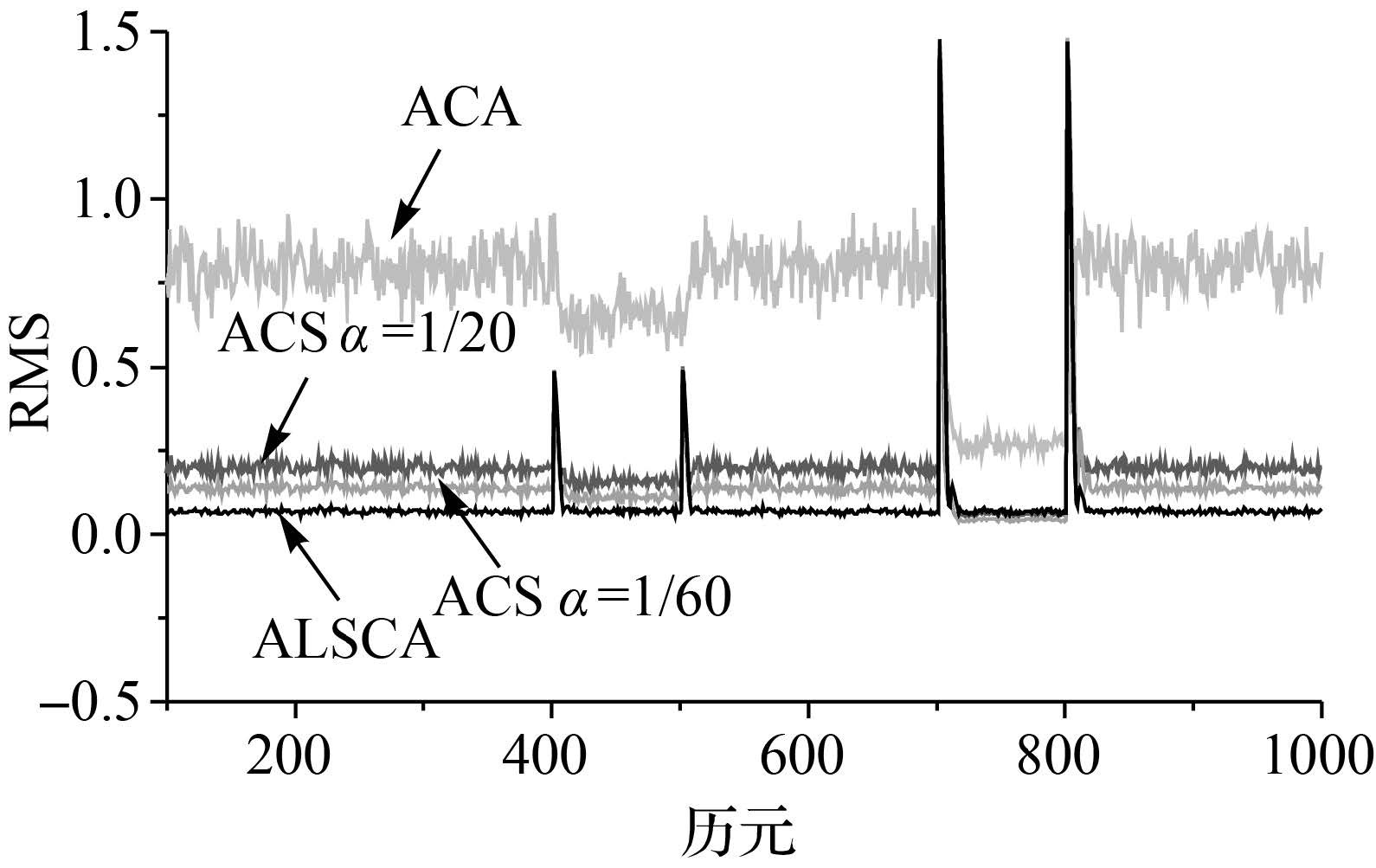
在实际应用中,机动频率α的取值一般是经验确定的,转弯机动α=1/60,逃避机动α=1/20,大气扰动α=1[15],同样最大加速度a±max也是根据相关应用而经验设定的。在仿真环境1中,采用ACS方法进行目标跟踪时,分别取机动频率α为1/20和1/60,最大加速度a±max=2,观测噪声协方差矩阵R=1;采用ACA方法进行目标跟踪时,取a±max=2;采用ALSCA方法进行目标跟踪时,取σ2=0.1,R=0.01。图 1-图 3给出了采用4种方法在环境1中的位置、速度和加速度的RMS。位置、速度和加速度的RMS的平均值(分别表示为xRMS、 和
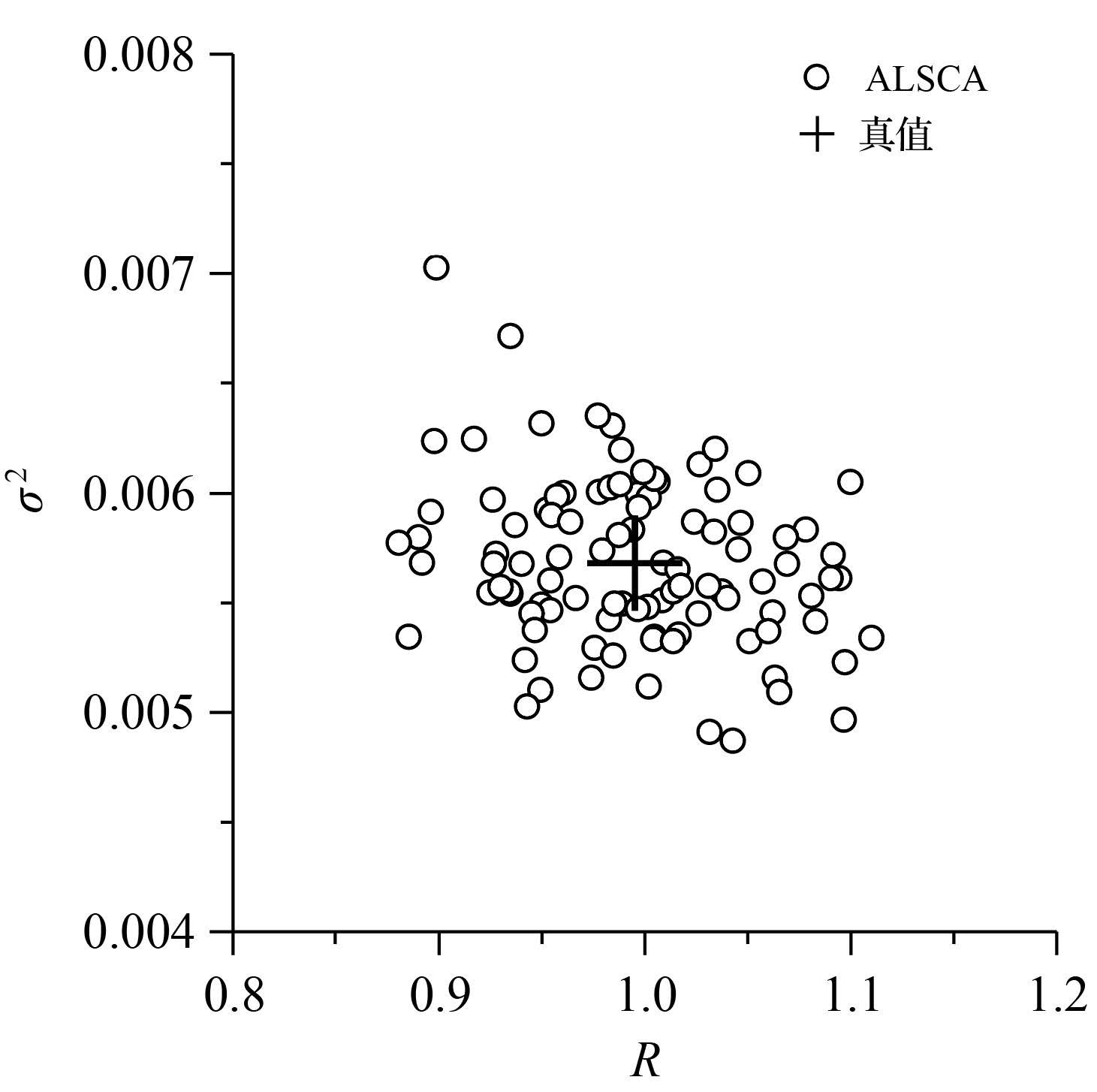
和 )见表 1。采用ALSCA方法估计的σ2和R见图 4,图中的“+”表示估值的平均值。
)见表 1。采用ALSCA方法估计的σ2和R见图 4,图中的“+”表示估值的平均值。
|
| 图 1 4种方法在环境1中的位置RMS Fig. 1 RMS of position for the four algorithms in case 1 |
|
| 图 2 4种方法在环境1中的速度RMS Fig. 2 RMS of velocity for the four algorithms in case 1 |
|
| 图 3 4种方法在环境1中的加速度RMS Fig. 3 RMS of acceleration for the four algorithms in case 1 |
| xRMS | 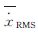 | 
| |
| ACS(α=1/20) | 0.82 | 0.56 | 0.19 |
| ACS(α=1/60) | 0.80 | 0.46 | 0.14 |
| ACA | 0.92 | 1.14 | 0.73 |
| ALSCA | 0.74 | 0.34 | 0.08 |
|
| 图 4 在环境1中σ2和R的估值 Fig. 4 Estimates of σ2 and R in case 1 |
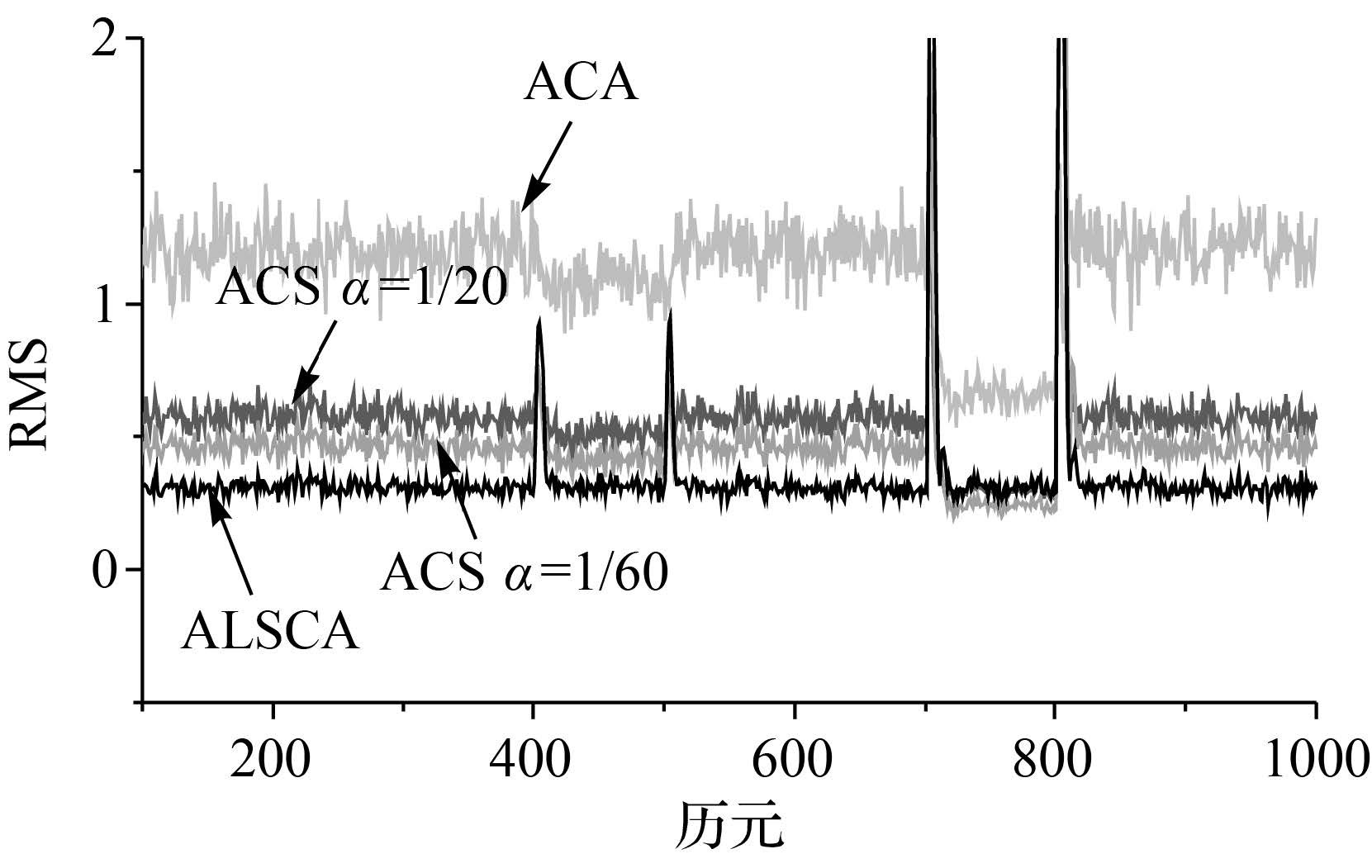
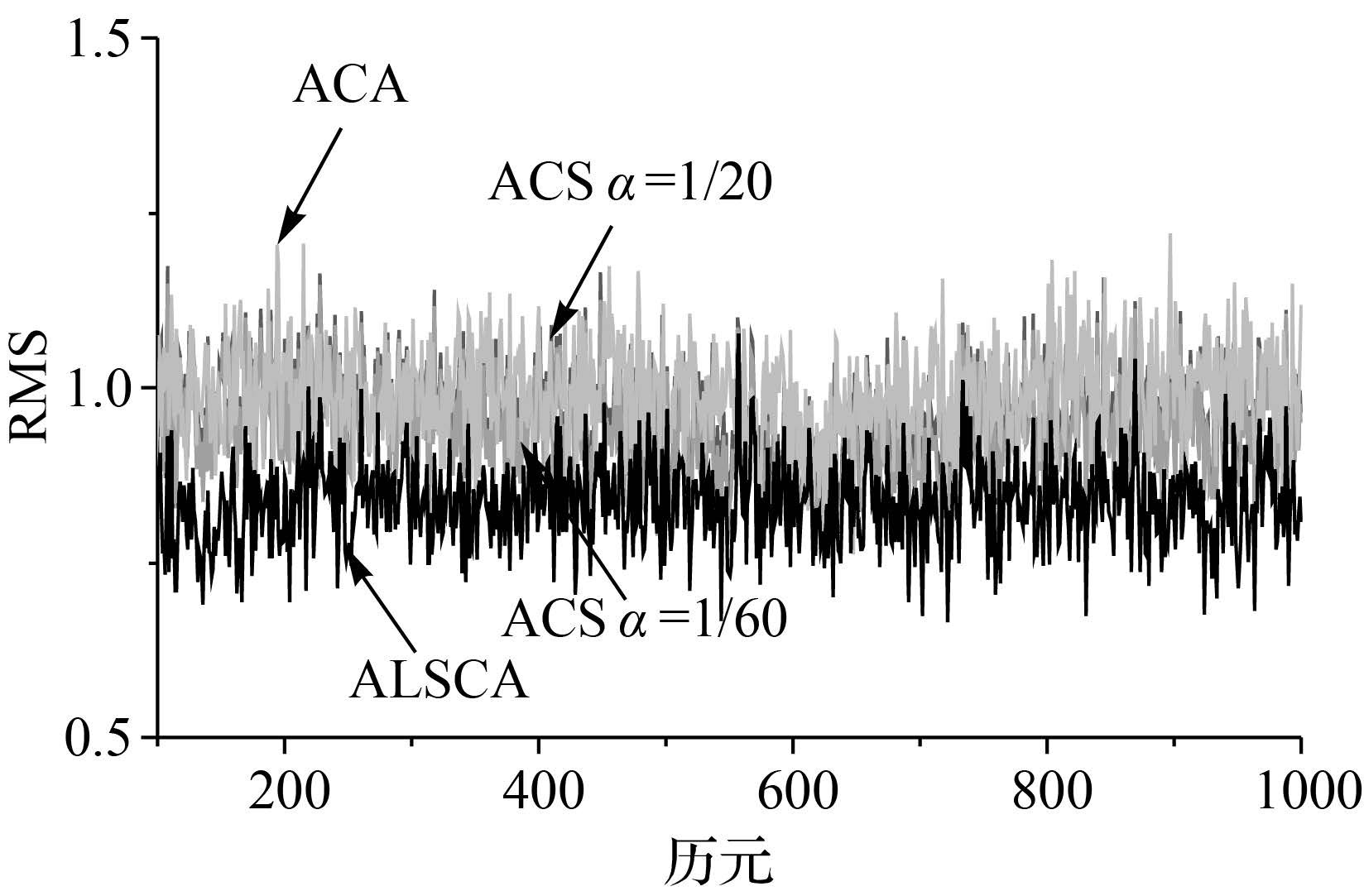
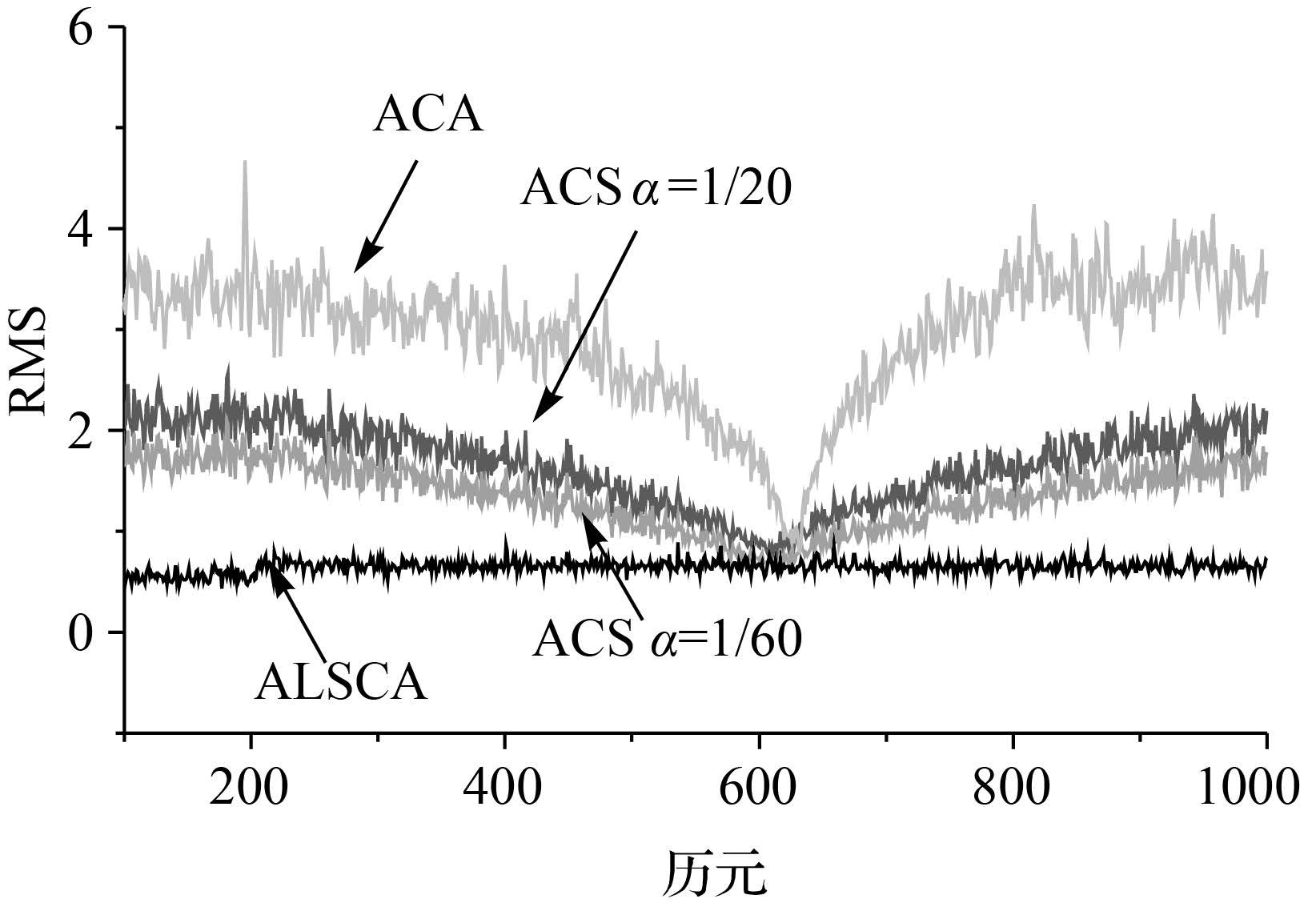
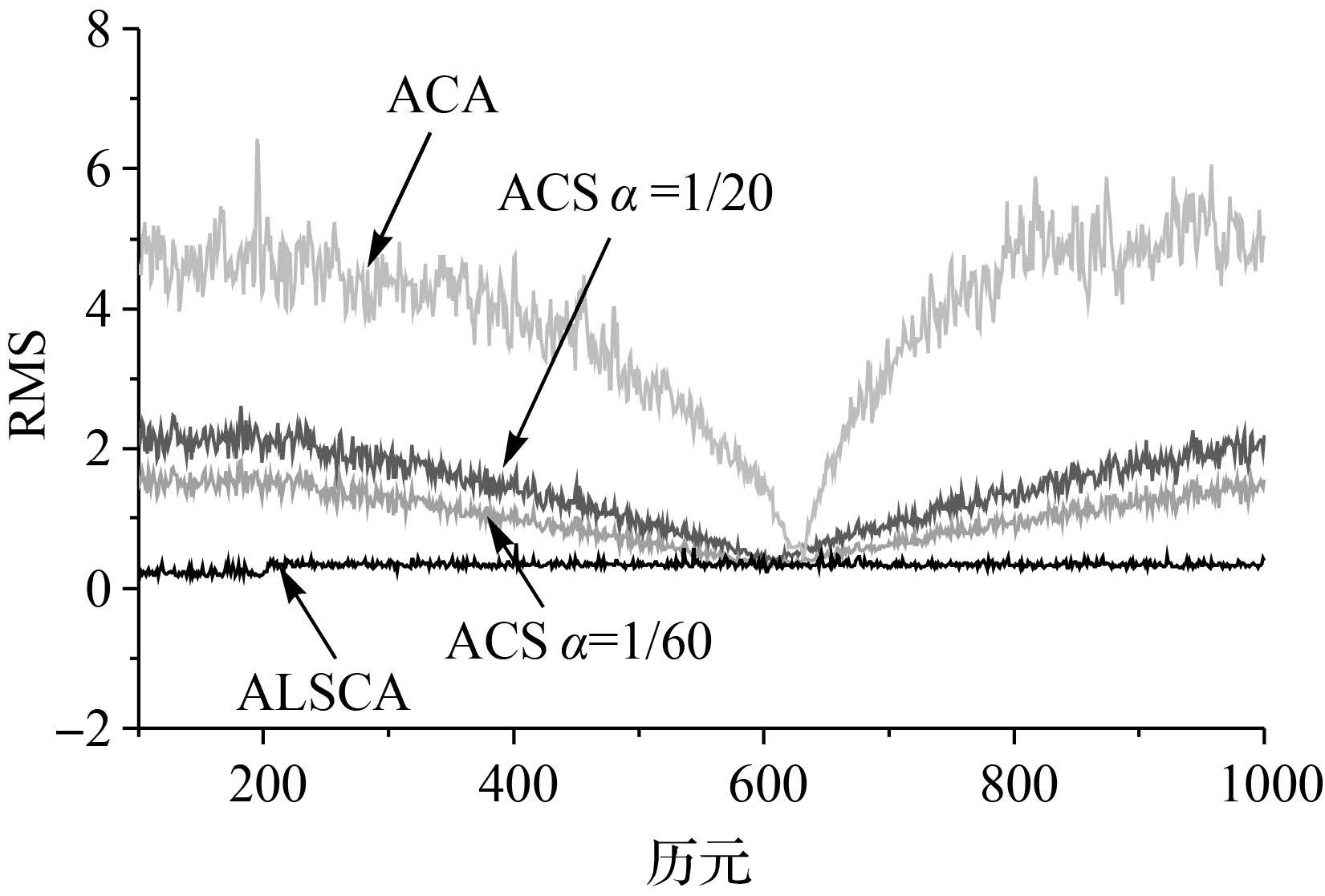
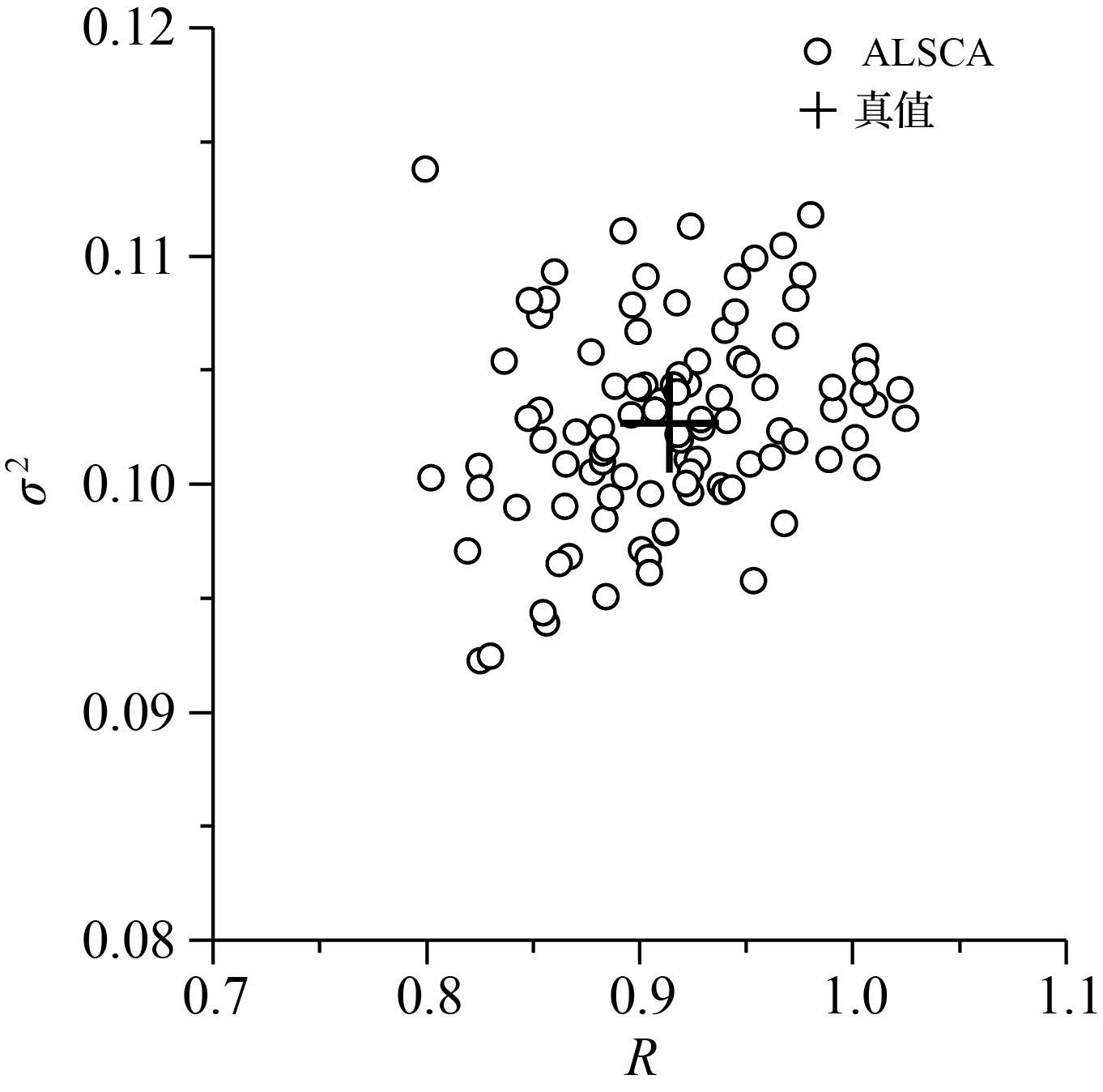
在仿真环境2中,采用ACS方法进行目标跟踪时,分别取机动频率α为1/20和1/60,最大加速度a±max=40,观测噪声协方差矩阵R=1;采用ACA方法进行目标跟踪时,取a±max=40;采用ALSCA方法进行目标跟踪时,取σ2=0.1,R=0.01。图 5-图 7给出了采用4种方法在环境2中的位置、速度和加速度的RMS。位置、速度和加速度的RMS的平均值见表 2。采用ALSCA方法估计的σ<sup>2和R见图 8,图中的“+”表示估值的平均值。
|
| 图 5 4种方法在环境2中的位置RMS Fig. 5 MS of position for the four algorithms in case 2 |
|
| 图 6 4种方法在环境2中的速度RMS Fig. 6 RMS of velocity for the four algorithms in case 2 |
|
| 图 7 4种方法在环境2中的加速度RMS Fig. 7 RMS of acceleration for the four algorithms in case 2 |
| xRMS |  | 
| |
| ACS(α=1/20) | 0.96 | 1.67 | 1.44 |
| ACS(α=1/60) | 0.94 | 1.36 | 1.01 |
| ACA | 0.99 | 2.99 | 3.98 |
| ALSCA | 0.83 | 0.65 | 0.33 |
|
| 图 8 在环境2中σ2和R的估值 Fig. 8 Estimated σ2 and R in case 2 |
从上述结果可以看出:
(1) ACS方法和ACA方法均非真正意义上的自适应滤波方法。应用ACS方法进行目标跟踪时,需要对机动频率、最大加速度和观测噪声协方差矩阵进行设定;应用ACA方法时,需要对最大加速度和观测噪声协方差矩阵进行设定。两种方法均只能对状态噪声协方差矩阵进行自适应估计,而无法对观测噪声协方差矩阵进行估计。不同的{机动频率、最大加速度、观测噪声协方差矩阵}或者{最大加速度、观测噪声协方差矩阵}的组合选择分别也会对ACS和ACA方法的目标跟踪精度带来影响。ALSCA方法虽然在应用时需先验设定常量方差和观测噪声协方差,但通过迭代计算后可避免先验参数误差对自适应滤波结果所带来的误差影响,其作用仅是用于启动算法而已。
(2) ACA方法的跟踪精度最差,ACS方法次之,而ALSCA估计精度最高。从图 1—图 4和表 1中可知,当载体加速度为阶跃加速度,即加加速度为零时,在加速度突变时刻ALSCA方法和ACS方法的误差基本相当,而在加速度稳定阶段,ALSCA方法的跟踪精度略优于ACS方法;从图 5—图 7和表 2可知,当载体加速度为变加速度时,即加加速度非零时,ACS和ACA方法在最大加速度a±max与真实加速度值最接近时,即在600 s时刻,两种方法的跟踪精度最优,特别是速度和加速度的跟踪精度最优;而随着最大加速度a±max与真实加速度值之间差值的增大时,两种方法的跟踪精度变差,在速度和加速度的跟踪精度上表现的特别明显。而ALSCA方法则整个变加速度阶段均具有较高的跟踪精度,其目标跟踪精度不会随着机动过程产生较大影响,且明显优于ACS方法和ACA方法。
(3) ALSCA方法能自适应估计未知的观测噪声协方差和常量方差。从图 4和图 8中可以看出,在两种仿真环境中,估计出的观测噪声协方差和常量方差具有较高的估计精度。当载体加速度为阶跃加速度,观测噪声协方差和常量方差估值的均值分别为1.00和0.005 7;当载体加速度为变加速度时,观测噪声协方差和常量方差估值的均值分别为0.91和0.10。当载体加速度为阶跃加速度,估计出的观测噪声协方差均值与真值一致,而当载体加速度为变加速度时,估计出的观测噪声协方差均值略微有偏,这主要是由于常加速度模型无法对变加速度过程进行精确描述。即使如此,采用估计出的观测噪声协方差和常量方差进行Kalman滤波时其目标跟踪精度较高。
(4) ALSCA方法无须对机动频率和最大加速度进行先验假设,只需先验设定常量方差和观测噪声协方差,且其滤波结果与先验参数的选取无关,通过迭代计算能有效地克服先验参数偏差所带来的误差影响,先验参数仅仅是作为启动程序的相关参数而已。
5 结 论通过对比“当前”统计模型和常加速度模型的Kalman滤波过程可以发现,两种方法的区别在于Kalman滤波增益的计算,如果合理地选择噪声协方差矩阵,两者将具有相当的目标跟踪能力。而不适当的参数的选择,也会对“当前”统计模型的自适应算法和常加速度模型自适应加速度算法的性能产生影响。采用常加速度模型对运动载体进行建模,顾及其状态噪声协方差矩阵满足特定结构,可将状态噪声协方差矩阵的求解转换为常值σ2的计算,因此本文提出了基于常加速度模型的简化自协方差最小二乘法。同时,对未知的状态噪声协方差和观测噪声协方差进行估计,采用估计出的状态噪声协方差进行Kalman滤波,避免了对机动频率和最大加速度的假设。仿真结果表明,当载体进行阶跃加速度运动和变加速度运动时,ALSCA方法目标跟踪精度均优于ACS方法和ACA方法。
| [1] | PAN Quan, LIANG Yan, YANG Feng, et al. Modern Target Tracking and Information Fusion[M]. Beijing: National Defense Industry Press, 2009. (潘泉, 梁彦, 杨峰, 等. 现代目标跟踪与信息融合[M]. 北京: 国防工业出版社, 2009.) |
| [2] | LI X R, JILKOV V P. A Survey of Maneuvering Target Tracking: Dynamic Models[C]//Proceedings of SPIE of Conference on Signal and Data Processing of Small Targets: 4048. Orlando:SPIE,2000: 212-236. |
| [3] | GAO Weiguang, YANG Yuanxi, ZHANG Shuangcheng. Adaptive Robust Kalman Filtering Based on the Current Statistical Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 15-18. (高为广, 杨元喜, 张双成. 基于当前加速度模型的抗差自适应 Kalman 滤波[J]. )测绘学报, 2006, 35(1): 15-18. |
| [4] | SINGER R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(4): 473-483. |
| [5] | GHOLSON N H, MOOSE R L. Maneuvering Target Tracking Using Adaptive State Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1977, 13(3): 310-317. |
| [6] | FANG Jiancheng. The Study and Application of the Optimal Estimation Theory and Method in Integrated Navigation System[D]. Nanjing: Dongnan University, 1998. (房建成. 最优估计理论与方法在组合导航中的应用研究[D].) 南京: 东南大学, 1998. |
| [7] | ZHOU Hongren. A “Current” Statistical Model and Adaptive Tracking Algorithm for Maneuvering Targets[J]. Acta Aeronautica et Astronautica Sinica, 1983, 4(1): 73-86. (周宏仁. 机动目标 “当前” 统计模型与自适应跟踪算法[J].) 航空学报, 1983, 4(1): 73-86. |
| [8] | ZHOU H, KUMAR K S P. An Adaptive Algorithm for Estimating the Acceleration of Highly Maneuvering Targets[C]//Proceedings of IEEE 1982 21st Conference on Decision and Control. [S. l.]: IEEE, 1982: 1133-1134. |
| [9] | MEHROTRA K, MAHAPATRA P R. A Jerk Model for Tracking Highly Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4): 1094-1105. |
| [10] | QIAO Xiangdong, WANG Baoshu. A CS-Jerk Model for Tracking Highly Maneuvering Targets[J]. Systems Engineering and Electronics, 2002, 24(6): 53-56. (乔向东, 王宝树. 高度机动目标的 “当前” 统计 Jerk 模型[J]. )系统工程与电子技术, 2002, 24(6): 53-56. |
| [11] | HOU Ming, WANG Peide. Statistical Model and Tracking Algorithm for Maneuvering Target[J]. Acta Aeronautica et Astronautica Sinica, 1990, 11(5): 282-287. (侯明, 王培德. 机动目标的模型与跟踪算法[J]. )航空学报, 1990, 11(5): 281-287. |
| [12] | JIA Zhijun, SHAN Ganlin, CHENG Xingya, et al. The Adaptive Extended Kalman Filter Algorithm in GPS Positioning for Moving Vehicles[J]. Journal of Ordnance Engineering College, 2001, 13(2): 39-43. (贾志军, 单甘霖, 程兴亚, 等. GPS 动态定位中的自适应扩展卡尔曼滤波算法[J]. )军械工程学院学报, 2001, 13(2): 39-43. |
| [13] | REN Shaowei, WANG Rui, ZHANG Pingding. An Adaptive Algorithm of Maneuvering Targets Tracking Based on Maneuvering Frequency[J]. Journal of Air Force Engineering University: Natural Science Edition, 2004, 5(5): 32-35. (任少伟, 王睿, 张平定. 基于机动频率自适应的目标跟踪算法[J]. )空军工程大学学报: 自然科学版, 2004, 5(5): 32-35. |
| [14] | WANG Junzheng, SHEN Wei, ZHAO Jiangbo. Adaptive Adjustment of Maneuvering Frequency in Target Tracking[J]. Transactions of Beijing Institute of Technology, 2007, 27(1): 38-41. (王军政, 沈伟, 赵江波. 机动目标跟踪中机动频率的自适应调整[J].) 北京理工大学学报, 2007, 27(1): 38-41. |
| [15] | LIU Wangsheng, LI Yaan, CUI Lin. Adaptive Strong Tracking Algorithm for Maneuvering Targets Based on Current Statistical Model[J]. Systems Engineering and Electronics, 2011, 33(9): 1937-1940. (刘望生, 李亚安, 崔琳. 基于当前统计模型的机动目标自适应强跟踪算法[J].) 系统工程与电子技术, 2011, 33(9): 1937-1940. |
| [16] | YANG Y X, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116. |
| [17] | YANG Y, GAO W. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. |
| [18] | ODELSON B J, RAJAMANI M R, RAWLINGS J B. A New Autocovariance Least-squares Method for Estimating Noise Covariances[J]. Automatica, 2006, 42(2): 303-308. |
| [19] | ODELSON B J, LUTZ A, RAWLINGS J B. The Autocovariance Least-squares Method for Estimating Covariances: Application to Model-based Control of Chemical Reactors[J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 532-540. |
| [20] | ABDEL-HAFEZ M F. The Autocovariance Least-squares Technique for GPS Measurement Noise Estimation[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 574-588. |
| [21] | LUO Zhicai, LIN Xu, ZHOU Boyang. Improved Algorithm of Autocovariance Least-squares Noise Estimation[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1164-1167. (罗志才, 林旭, 周波阳. 自协方差最小二乘噪声估计的改进算法[J]. )武汉大学学报: 信息科学版, 2012, 37(10): 1164-1167. |
| [22] | LI X R, ZWI X, ZWANG Y. Multiple-model Estimation with Variable Structure. Ⅲ. Model-group Switching Algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 225-241. |