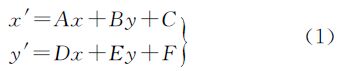2. 常州市基础地理勘测中心,江苏 常州 213003;
3. 南通大学 地理科学学院,江苏 南通 226007
2. Basic Geographic Surveying Center of Changzhou, Changzhou 213003, China;
3. School of Geographic Science, Nantong University, Nantong 226007, China
空间数据库的建立及更新需应用和集成多源地理信息数据,这些数据往往存在不同主题、不同比例尺、不同时态数据匹配的不一致问题,如地理匹配关系矛盾、要素表达不一致、邻近关系冲突、拓扑结构不一致等,而一致性是空间分析决策、空间数据挖掘等过程中应考虑的重要因素。因此,如何发现、纠正数据的不一致并对异源数据进行有效的匹配成为当前GIS领域的研究热点[1]。地图数据库中,等高线与河流是两种基本的地理要素类型,两者之间有着显著的空间依赖性,在地图上具体表现为河流通常与成组等高线的谷底线重合[2, 3],但由于数据采集方式、更新周期的不同,等高线与河流数据在集成、更新过程中往往产生河流“爬坡”、等高线“入水”等违背自然规律的现象[1];制图综合中采用“分治”[4]策略分别对等高线和河流进行综合后也会产生不一致问题,是地图综合所面临的难题之一[2]。
目前对等高线与河流空间关系不一致的探测和修正主要采用目视判读与人工编辑的方法,即通过观察与河流相交的等高线组的整体形态特征来判断出近似山谷点和山谷线,根据经验目估山谷线和河流之间的偏离程度并判断其一致性。由于依赖于作业员的经验且需要大量的人工编辑,因此容易错判、漏判且效率较低[5]。文献[5]提出河流与山谷线的一致性检测方法,该方法基于矢量投影法提取山谷点并计算近似山谷线,通过计算其到河流的最小垂距来检测空间一致性,但未提及自动改正方案。文献[6]利用向量变换方法对局部等高线进行修正以消除与河流的冲突,方法简单运行速度快,但该方法需要在运行前指定作为控制线的河流和需要被修正的等高线且只适用于等高线与河流偏离较小的情况。文献[1]提出等高线与水网匹配的一致性改正方法,即利用Delaunay三角网对等高线进行弯曲分析提取地形特征点,基于河流分布与谷地走势的相关性识别两者间的一致性并建立匹配关系,利用仿射变换实现水网与等高线的一致化改正,探讨移位水网和移位等高线两种匹配方式,但在等高线成组分布且形状变化较大、水网与谷底线相距较远时,移位等高线的方法还存在产生二次相交等次生冲突或原有冲突未解决的问题,需要探索更好的移位方法。
移位等高线或移位河流这两种方法的选择取决于数据的定位精度及数据的具体应用背景[1]。等高线的定位精度受获取方法和地图比例尺的影响,运用航测方法获取的高于运用散点插绘方法获取的,大比例尺的高于小比例尺的[7],因此地理要素精度的确定需要视具体情况而定。一般情况下,河流数据的精度高于等高线数据的精度,有时两者的精度难以确定,如地图制图综合中对等高线和河流数据化简后产生了空间冲突[2],此时很难确定等高线与河流哪个精度更高。河流作为地图内容的控制“骨架”对其他要素有一定的制约作用,其重要性通常高于等高线[7, 8]。因此,在河流数据获取方法的精度高于等高线等可以确定河流精度更高的情况下,应该保持河流而移位等高线;在数据来源、比例尺等相同河流与等高线的精度相近或者在地图综合产生空间冲突而无法确定精度大小时,考虑要素重要性,也应该优先保持河流位置;只有在其他能够明确等高线数据精度高于河流的情况下才适合移位河流。
完备合理的移位模型在避免产生次生冲突同时也需要保持原有的空间形态和分布模式[9, 10],考虑到等高线的形态结构,仅通过移位其局部或单个弯曲无法达到一致化的效果,但移位范围过大又难以进行控制,往往出现相邻等高线相交等空间冲突。因此移位等高线匹配至河流的关键是选择合适的移位范围并确立合理的移位函数模型。本文以等高线一个完整弯曲弧段为最小单元,综合考虑多方面约束因素动态确定各点仿射变换移位模型,有效实现等高线移位的质量控制,能够较好地完成等高线匹配至河流的一致性改正。
2 相关概念与方法基础 2.1 相关概念 2.1.1 坡段
等高线在地图上表现为起伏波状,起伏的最高点或最低点一般为山谷点或山脊点,这些地形特征点将等高线分割为多段,在此将这样的每一条等高线段称为坡段。若该坡段两端的地形特征点为A、B,则将该坡段表示为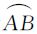 。
。
相邻两个坡段呈弧形“V”或其倒置状,称为坡弧。成组相关的坡弧在自然地形中反映一个完整的坡面,是地貌的基本构成部分。设一个坡弧上的地形特征点依次为A、B、C 3点,则该坡弧可表示为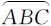 ,包括
,包括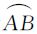 和
和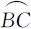 两个坡段。
两个坡段。
地图上河流应沿山谷点延伸与山谷线近似重合,可求取与河流相交的等高线上距离河流最近的山谷点到河流的垂距,利用该垂距来判断河流是否偏离山谷线更符合人的认知习惯[5],也易于操作,匹配时将最近山谷点移位至垂足位置即可。但由于等高线成组分布且形态变化较大,移位易产生数据冲突[1];移位范围过小难以达到移位目的,范围过大则难以控制全局质量。因此等高线移位的难点在于确定移位范围和避免空间冲突。坡弧是等高线最为完整的局部形态,反映在地形上也是一个完整的坡面,以其作为最小移位单元便于过程控制;鉴于地图上成组相邻等高线近似平行,综合考虑角度、位置、缩放等约束,有针对性的确立移位模型可避免相邻等高线相交等冲突。仿射变换是坐标变换效果较好的常用方法之一[11],考虑以上多个因素建立模型可兼顾避免空间冲突和保持等高线局部形态,同时可增强方法的普适性以适应不同情形等高线数据的移位。综上,本文尝试通过可控制的移位范围和多约束条件下的移位模型实现等高线与河流的一致性改正。
2.3 地形特征及其提取自然长期作用形成的地形有其特征可循,其中山脊线和山谷线在几何上构成了地形起伏变化的分界线或骨架线,在地形表示方面有极其重要的作用;另一方面,山脊线的分水性和山谷线的合水性等地理特性又使其在工程应用方面有着特殊意义[12]。具体表现在地图上,地形可由等高线表示,山脊线和山谷线与等高线相交于山脊点和山谷点;河流在山地沿山谷发育并沿山谷点延伸。因此,要移位等高线匹配河流首先要根据地形特征判断数据一致性,再将相关山谷点移位至河流上并协同移位其他特征点,而地形特征的提取成为一致性改正的必要前提。
目前利用等高线提取地形特征点、线已有了诸多可借鉴的研究成果[12, 13, 14, 15, 16, 17, 18]。较为简单的方法是利用Split方法筛选等高线上的特征点,判断特征点处张角范围内相邻等高线的高程与该点高程对比识别出山脊点和山谷点等地形特征点,利用这些点再生成山脊线和山谷线,具体实现方案可参考文献[15]。
2.4 仿射变换仿射变换是基于仿射坐标系建立的一种坐标变换数学模型,是经过坐标系的平移、比例、旋转、对称和错切等复合变换得到的[19],广泛应用于坐标变换和图形图像校正等领域。若设某点初始坐标为(x,y),移位后坐标为(x′,y′),则仿射变换基本模型可表示为[20]
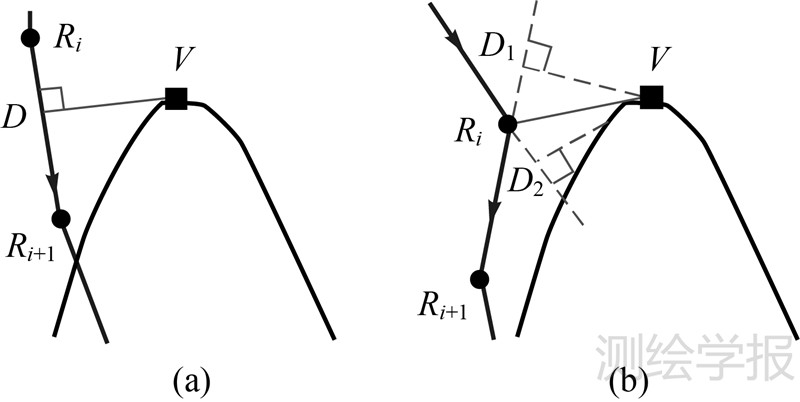
仿射变换要求至少有3个定向点,本文希望通过考虑多因素动态确定等高线上不同位置特征点的仿射变换模型,以增强一致性匹配过程中等高线移位的质量控制。 3 等高线匹配与河流的一致性改正 3.1 等高线与河流不一致性探测正常情况下河流应沿山谷点延伸并与山谷线大致重合,当等高线与河流数据不一致时会出现河流偏移山谷点。在对等高线与河流的不一致性进行探测时先求取与某条河流相交的等高线组,然后找到每条等高线上到该河流距离最近的山谷点,即通过计算各山谷点到河流的垂距,其中垂距最小的山谷点即为要移位的目标匹配山谷点。需要说明的是,求取某一山谷点V到某一河流的垂距时,需判断垂足D是否在河流上,若在河流上则VD为山谷点V的移位,如图 1(a)所示;若不在河流上,则求取构成河流的特征点中到山谷点V距离最小的一个记为Ri,则VRi为V的移位,如图 1(b)所示。
|
| 图 1 不一致性探测 Fig. 1 Detecting the inconsistency |
但是仅通过单条等高线获取目标山谷点存在不足,上述匹配过程仅考虑了单个水网和等高线交点与谷底点间的位置关系,未顾及水网流向及整体匹配情况[1],求取目标山谷点可能会出现个别错误,如图 2所示。由于复杂的地形情况以及数据误差这种情况是难以避免的,为确保获取正确的匹配关系,在求取全部需移位的山谷点集后还需进一步检查改正。可将水网和等高线交点与对应的目标山谷点连接来近似表示水网及山谷线,并连接山谷线两端点与邻近水网节点,通过计算相邻有向线段顺时针方向夹角,并进行对比找到错误匹配并修正[1]。也可利用等高线提取的山谷线,求取需要移位至河流的山谷点集所集中在的山谷线,进而对所求取的山谷点集进行改正。
3.2 等高线移位坡弧是等高线较为完整的局部形态,无论从等高线在地图上的几何特征表现还是地理上的地形特征来看,坡弧都是最稳定的局部构成。坡弧由两个坡段按一定角度组合而成,类似“脚架”结构,连接坡弧上的3个地形特征点形成一个三角形的稳定结构,因此以坡弧作为等高线与河流一致性匹配时的基本单元是较为合适的选择。考虑直接对每个坡弧应用同一个仿射变换模型进行移位的明显不足[1],本研究对等高线不同位置的特征点综合考虑相对移位角度、地形特征点相对位置、局部综合形态等相关因素,单独确定移位模型。
一般而言,山谷点移位至其到河流的垂足,其移位幅度是最大的,需要按照一定规则建立坡弧上其余各特征点与山谷点移位的对应关系,考虑相邻坡弧的连动机制,同时还应顾及构成坡弧的两个坡段形态的大致对称性以区别处理。综合以上因素,本研究确定等高线匹配到河流的移位模型的角度、位置和缩放等约束条件。
3.2.1 角度约束
取坡弧R1VR2,其中R1、R2为山脊点,V为山谷点,按照上述不一致性探测所确定的移位将V移位至河流上的V′点,以其向两侧到两个山脊点的移位幅度应逐渐减小,以实现范围控制并维持整个坡弧形态和结构的稳定。取两山脊点R1、R2连线的中点Rm,连接Rm、V和Rm、V′,则坡段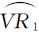 和
和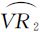 以RmV为轴大致对称。设定两坡段上任一特征点P移位的角度约束参数α,则坡段
以RmV为轴大致对称。设定两坡段上任一特征点P移位的角度约束参数α,则坡段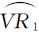 上特征点移位的角度约束参数α1=∠R1RmPi/∠R1RmV=∠VRmT/∠VRmV′,对应的有坡段
上特征点移位的角度约束参数α1=∠R1RmPi/∠R1RmV=∠VRmT/∠VRmV′,对应的有坡段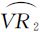 上特征点移位的角度约束参数α2=∠R2RmPj/∠R2RmV=∠VRmT/∠VRmV′,根据该角度约束参数可确定T点位置,具体如图 3所示。最后通过V、Rm和T 3点利用基线旋转和缩放的方式确定P点的仿射变换矩阵。可以看出P点的仿射变换模型与V点移位到T点的变换相同,通过这一措施使得山谷点V的移位变形递减分配到其余各点,并保持其相邻两山脊点的位置不动使得移位范围控制在坡弧上。
上特征点移位的角度约束参数α2=∠R2RmPj/∠R2RmV=∠VRmT/∠VRmV′,根据该角度约束参数可确定T点位置,具体如图 3所示。最后通过V、Rm和T 3点利用基线旋转和缩放的方式确定P点的仿射变换矩阵。可以看出P点的仿射变换模型与V点移位到T点的变换相同,通过这一措施使得山谷点V的移位变形递减分配到其余各点,并保持其相邻两山脊点的位置不动使得移位范围控制在坡弧上。

|
| 图 3 确立仿射变换模型 Fig. 3 Building the affine transformation model |
地形起伏中的凹陷和凸起即山谷和山脊是相互依存的[21],某一坡弧移位后需要对两侧相邻的坡弧作适当调整,以维持整体坡弧形状,因此还需要对移位造成影响的两个邻近坡弧进行“惯性移位”。具体方法为对需要匹配到河流的坡弧移位前,先计算临近山脊点相对于两侧相邻山谷点的相对位置,即由山脊点R向V1V2作垂线垂足为M,得到山脊点相对于相邻两个山谷点的位置约束参数β=V1M/V2M,要求山谷点移位后V1′M′/V2′M′=β,从M′点作垂线交于V1′V2′的平行线RR′于R′,RR′就为山脊点R的移位。同样按照上述角度约束确定移位仿射变换模型的方法,对相邻以山脊点为中心的坡弧进行移位。特殊情况下当相邻两个山谷点所在的坡弧都需要移位时,对其重合部分组成的坡弧也按照上述位置约束移位,具体如图 4所示,此时双方移位会使中间坡弧变形引起相关山谷和山脊形态的变化,类似按照上述方法对移位后的中间坡弧按照位置约束重新调整,得到如图 4(b)的结果。

|
| 图 4 一致性改正过程 Fig. 4 Process of consistency correcting |
考虑以上两个移位约束确定移位模型进行等高线到河流的匹配移位后,对比结果发现相对河流只是稍偏离山谷点但整体走向与山脊线近似平行的情形匹配效果较好,本研究的移位策略已初见成效,方法可行。但当河流偏移更多,与等高线组中部分等高线相交于邻近山脊点附近甚至跨过山脊点,此时数据误差较大,更为复杂的情况下,河流部分或整体偏移至山脊线位置,且所经等高线密集且弯曲较大,单纯地利用角度和位置约束进行一致性改正后出现等高线相交、等高线局部与河流重合等次生冲突现象,如图 5所示(图中方形点为山谷点,三角点为山脊点)。从整体形态可以看出,坡弧的两个构成坡段的中部向同一侧扭曲,说明需要加强每个坡段中部的移位幅度,同时仍需考虑对称坡段的协同移位,以解决中部变形和空间冲突问题。

|
| 图 5 等高线移位后产生冲突 Fig. 5 Conflicts generated from displacing the contours |
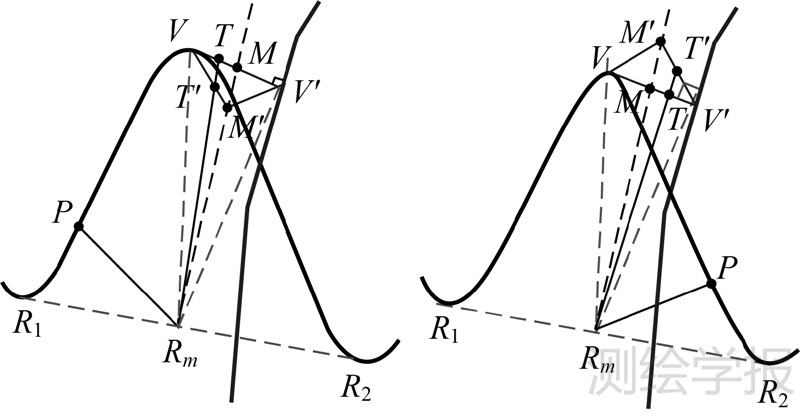
要解决坡弧的两个坡段中部向同一侧变形的问题,需增加坡段中部特征点的位移量控制。若以山谷点为中心,从整体形态保持方面考虑其移位角度和距离直接影响两侧特征点的移位,且其移位后两侧的坡段移位是随之对应进行的,以此为出发点在确定各特征点移位角度的基础上增加位移的缩放处理。V移位至V′的角度为∠VRmV′,取其角平分线为中心轴与VV′交于M,以RmM为基准轴设定坡弧每个坡段上等高线特征点移位的缩放约束参数μ=MM′/RmM。由于相对于河流位置的不同,与河流相交的那一侧的坡段必然距离河流更近,其位移量应增大,因此延长RmM至M′使MM′/RmM=μ,如图 6(b)所示;相反另一条坡段中部位移量应缩减,M′点的位置应该在RmM上同样使MM′/RmM=μ(由大量试验验证得μ的取值以χ=VV′/R1R2的0.5倍为宜),如图 6(a)所示。由此连接M′和V、V′两点得到该坡弧移位的缩放三角形ΔVM′V′,结合两平坡段上各特征点P的移位角度约束参数α=∠R1RmP/∠R1RmV=∠VRmT/∠VRmV′得到T点,RmT(或取其延长线)交ΔVMV′的另一边于T′点,由V、Rm、T′ 3点最终确定P点的仿射变换模型。
|
| 图 6 移位缩放比例系数计算 Fig. 6 Calculating the zoom coefficient of displacement |
加入缩放考虑后,通过角度、位置、缩放3参数约束建立移位模型对各种情形进行一致性匹配改正,得到如图 7所示的结果,可以看出移位后未产生新的空间冲突,且等高线的形态保持较好。
|
| 图 7 一致性改正结果 Fig. 7 Results of consistency correcting |
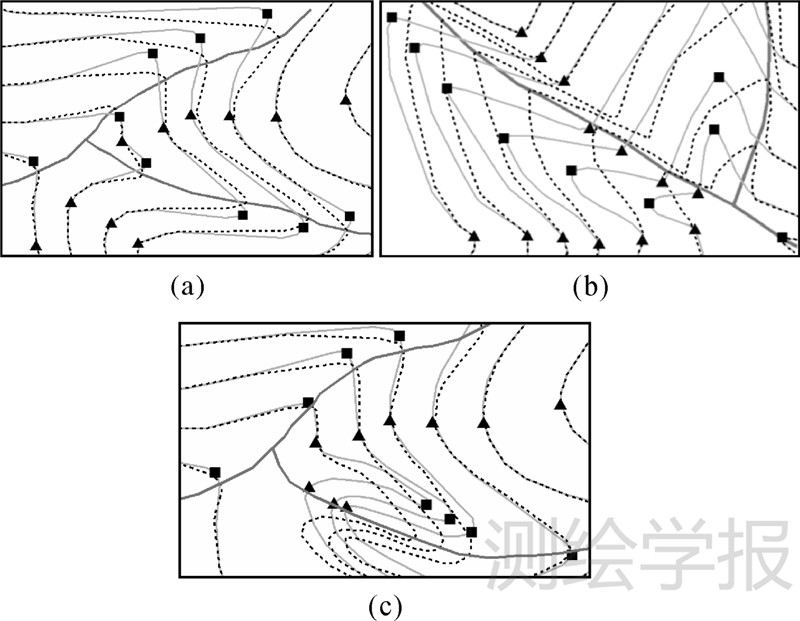
本文选取多组试验数据,综合应用上述方法对河流与等高线的一致性进行探测和匹配,如图 8为选取的局部匹配效果图,图中深色曲线为改正后的等高线。可以看出经过本文的方法改正后,等高线与河流的空间一致性明显提高,试验也发现对于狭长型谷地等高线等特殊地形情况,本方法也较好地完成了一致性改正,如图 8(b)所示。

|
| 图 8 试验结果 Fig. 8 Result of experiments |
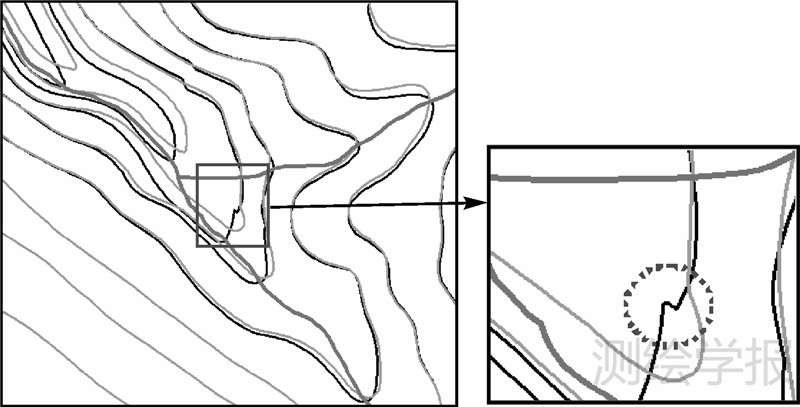
试验结果中出现个别等高线移位后特征点的跳动现象,如图 9所示,在等高线局部走势较为平缓特征点较少时,该部分多点移位幅度过大会出现此现象。这是动态计算每点的移位模型所造成的,但从图中看出移位后的整体形态是符合要求的,且跳动点的数量较少,幅度较小,可通过化简处理解决该问题。
|
| 图 9 等高线移位的局部跳动现象 Fig. 9 Local flop in displacement of contour |
此外由于只对与河流相交的等高线移位,当数据的不一致性偏差较大时,最外缘等高线由于移位较大可能与外围未移位的等高线相交。虽然此种情况较少但是仍然影响数据质量,需要增加对边缘位置的移位控制,或者进一步考虑带动边缘等高线移位的一体化改正方案,这些将在以后的研究中作进一步探讨。
5 结 论本文在现有等高线与河流不一致性探测和匹配方法的基础上,具体针对等高线匹配到河流的一致性改正方案进行了探讨,提出等高线移位的角度、位置、缩放3个约束参数,有效确立了对每条坡段上每个数据点的移位模型,解决了移位过程中的空间冲突问题,完成了等高线到河流的一致性匹配。需要说明的是本文研究的前提是山谷点虽然偏离河流,但河流仍距离其应在山谷线上的大部分山谷点最近,否则无法正确匹配。
| [1] | YANG Min, AI Tinghua, LIU Pengcheng, et al. The Matching and Consistency Correcting in the Integration of Contour and River Network[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 152-158.(杨敏, 艾廷华, 刘鹏程, 等. 等高线与水网数据集成中的匹配及一致性改正[J]. 测绘学报, 2012, 41(1): 152-158.) |
| [2] | LONG Yi, CAO Yang, SHEN Jie, et al. Cooperative Generalization Method of Contour Cluster and River Network Based on Constrained D-TIN[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 379-385.(龙毅, 曹阳, 沈婕, 等. 基于约束D-TIN的等高线簇与河网协同综合方法[J]. 测绘学报, 2011, 40(3): 379-385.) |
| [3] | SHU Fangguo, LONG Yi, ZHOU Tong, et al. An Extraction Method of Catchment Basin Based on Cooperation of Contour Cluster and River Network in River Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):774-781.(舒方国, 龙毅, 周侗, 等. 地图水系综合中等高线簇与河网协同的汇水区域提取方法[J]. 测绘学报, 2013,42(5):774-781.) |
| [4] | WU Hehai. Research on Fundamental Theory and Technical Approaches of Automated Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 377-386.(毋河海. 地图信息自动综合基本问题研究[J]. 武汉测绘科技大学学报, 2000, 25(5): 377-386.) |
| [5] | LIU Wanzeng, CHEN Jun, DENG Kazhong, et al. Detecting the Spatial Inconsistency between the Updated Rivers and Valleys[J]. Journal of Image and Graphics, 2008, 13(5): 1003-1008.(刘万增, 陈军, 邓喀中, 等. 数据库更新中河流与山谷线一致性检测[J]. 中国图象图形学报, 2008, 13(5): 1003-1008.) |
| [6] | WANG Qiang, CAO Hui. Automatic Detection and Correction of Spatial Confilct between River Line and Valley Line on Digital Topographic Maps[J]. Bulletin of Surveying and Mapping, 2010(12):58-61.(王强, 曹辉. 数字地形图中河流线与谷底线空间冲突自动检测及纠正[J]. 测绘通报, 2010(12):58-61.) |
| [7] | WANG Jiayao, SUN Qun, WANG Guangxia, et al. Principle and Method of Cartography[M]. Beijing: Science Press, 2006:209-339.(王家耀,孙群, 王光霞,等. 地图学原理与方法[M]. 北京: 科学出版社, 2006:209-339.) |
| [8] | QIAN Haizhong, WU Fang, GUO Jian, et al. Spatial Data Checking with Generalization Knowledge[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(2):184-190.(钱海忠, 武芳, 郭健, 等. 基于制图综合知识的空间数据检查[J]. 测绘学报, 2006,35(2):184-190.) |
| [9] | ZHOU Qi, AI Tinghua, ZHANG Xiang. A Displacement Field Model to Resolve Multiple Spatial Conflicts[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4):615-620.(周启, 艾廷华, 张翔. 面向多重空间冲突解决的移位场模型[J]. 测绘学报, 2013,42(4):615-620.) |
| [10] | ANSELIN L, LONGLEY P A, GOODCHILD M F, et al. Geographical Information System: Principles, Techniques, Management and Applications[M]. New York:John Wiley & Sons, 1999. |
| [11] | ZHONG Cheng, LI Hui, LI Zonghua, et al. Affects of Geometrical Conditions and Transformation Methods on Quality of Coordinate Transformation[J]. Acta Geodaetica Cartographica Sinica, 2010, 39(6): 642-648.(钟成, 李卉, 李宗华, 等. 几何条件与变换模型对坐标变换质量的影响[J]. 测绘学报, 2010, 39(6): 642-648.) |
| [12] | HUANG Peizhi. A New Method for Extracting Terrain Feature Lines from Digitized Terrain Data[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3): 247-252.(黄培之. 提取山脊线和山谷线的一种新方法[J]. 武汉大学学报: 信息科学版, 2001, 26(3): 247-252.) |
| [13] | YU Shengchen, LIU Dayou,LIU Hong. Auto-recognizing Ridge lines and Ravine Lines by Computer[J]. Journal of Image and Graphics, 1999, 4(8): 693-696.(余生晨, 刘大有, 刘洪. 山脊线与山谷线的计算机自动检测[J]. 中国图象图形学报: A版, 1999, 4(8): 693-696.) |
| [14] | AI Tinghua, ZHU Guorui, ZHANG Genshou. Extraction of Landform Features and Organization of Valley Treestructure Based on Delaunay Triangulation Model[J].Journal of Remote Sensing, 2003, 7(4): 292-298.(艾廷华, 祝国瑞, 张根寿. 基于 Delaunay 三角网模型的等高线地形特征提取及谷地树结构化组织[J]. 遥感学报, 2003, 7(4): 292-298.) |
| [15] | JIN Hailiang, KANG Jianrong, GAO Jingxiang. Research on the Algorithm of Extracting Ridge and Valley Lines Using Contour Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 809-812.(靳海亮, 康建荣, 高井祥. 利用等高线数据提取山脊 (谷) 线算法研究[J]. 武汉大学学报:信息科学版, 2005, 30(9): 809-812.) |
| [16] | GUO Qingsheng, YANG Zuqiao, FENG Ke. Extracting Topographic Characteristic Line from Contours[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 253-256.(郭庆胜, 杨族桥, 冯科. 基于等高线提取地形特征线的研究[J]. 武汉大学学报: 信息科学版, 2008, 33(3): 253-256.) |
| [17] | ZHANG Yao, FAN Hong, LI Yu’e. A Method of Terrain Feature Extraction Based on Contour[J]. Acta Geodaetica et Cartographica Sinica,2013, 4(42): 574-580.(张尧, 樊红, 李玉娥. 一种基于等高线的地形特征线提取方法[J]. 测绘学报, 2013, 4(42): 574-580.) |
| [18] | AI T. The Drainage Network Extraction from Contour Lines for Contour Line Generalization[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007,62(2):93-103. |
| [19] | GUO Jinyun, ZHU Mingfa, XU Panlin. Comparison between the Affine Transformation and the SimilarityTransformation and Its Analysis[J]. Bulletin of Surveying and Mapping, 2001 (4):23-24, 27.(郭金运, 朱明法, 徐泮林. 地图数据几何纠正时仿射变换与相似变换的对比分析[J]. 测绘通报, 2001 (4):23-24, 27.) |
| [20] | ZHOU Wei, ZHANG Yanyan, LONG Yi. The Methods and Implement of Coordinates Conversion for Graphs[J]. Geo-Information Science, 2007, 9(2): 101-105.(周卫, 张彦彦, 龙毅. 图形坐标转换方法与实现[J]. 地球信息科学, 2007, 9(2): 101-105.) |
| [21] | LI Wenjing, QIU Jia, LIN Zhiyong, et al. Approach of Curve Bends Recognition and Contour Cluster Structurization[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 295-303.(李雯静, 邱佳, 林志勇, 等. 曲线弯曲识别与等高线簇结构化方法[J]. 测绘学报, 2013, 42(2): 295-303.) |