以数字化的方式表达城市空间信息,为智能化交通、动态导航和物流配送等日常需求提供最优决策支持是当前数字城市相关研究和信息化服务应用的热点问题,可达性作为上述热点问题研究中的主要空间动因,是空间行为和空间决策的决定性因素。可达性研究自文献[1]提出引力模型描述商业分布以来,逐渐发展成为一个重要的基础概念而被广泛地应用于交通运输经济学、城市规划、地理学等相关研究领域。可达性是衡量城市居民与社会经济活动之间地理关系深度和广度的指标[2]。时空可达性[3, 4]是一种从个体角度出发,综合考虑空间因素和时间因素,研究在特定的时空约束下的可达时空范围的方法,该方法将GIS技术和时间地理学的概念结合起来研究交通网络可达性[5]。这种可达性研究方法是以20世纪60年代末文献[6]提出的时间地理学为基础的,文献[7]利用等时线将时空地理学框架和可达性度量方法融合在一起分析交通网络的可达范围。
从文献分析,近年来对等时线的研究主要集中在4个方面:①利用等时线衡量时间成本,研究交通网络可达性,例如文献[8]使用等时线的方法进行交通运输成本的分析,利用GIS技术生成等时区域表达交通运输成本;②服务设施可达性评价,例如文献[9]用等时线来评估城市设施对于不配备小汽车的家庭妇女的可达性;③建立桌面或网页GIS系统辅助居民出行决策及城市交通规划,例如文献[10]创建的MySociety,利用等时线提供房价估测,辅助规划公路铁路网络,出行决策等服务,文献[11]的FromToMap LBS网站对OSM欧洲范围内GB级别的道路实现了可达性分析服务,伦敦交通局行程计划系统提供各种个性化定制估计行程时间的服务[12];④高效率的等时线生成算法研究,文献[13]制作一种在多模态联运网络下,结合步行和公共交通系统计算等时线的系统,但该系统只表示一段时间内可以到达的道路弧段,没有生成等时区域,并且算法效率较低。为了确定等时区域范围,文献[14]设计了基于线的和基于面的两种算法。文献[15]重新定义多模态联运网络下的等时线,将交通分为在时间和空间上分别离散和连续的模态,提出了基于Dijkstra算法的多模态联运网络扩展(MINE)的等时线计算算法。之后又对MINE算法进一步优化产生高效和可扩展的MINEX算法[16]。等时线辅助可达性分析的应用研究成果丰富,这些研究通常将等时线作为一种工具来解决某一具体问题,而对等时线的特性及意义关注较少。等时线生成算法的研究主要是基于Dijkstra算法[17],该算法的主要限制是路径向各个方向扩展,并且难以负载约束条件,这样的算法机制忽略了等时线与道路网络结构本身的内在联系。
本研究对等时线展开系统的研究,主要包括以下两方面:首先,对网络栅格化模型进行改进,提出生成等时线的水流扩展算法(简称水流法),针对等时线扩展考虑其独特的约束条件,包括道路网络状况(通行条件、通行能力等)、移动条件及时间分段等;其次,类比等高线表示地貌特征的分析方法,选取特定区域生成等时线,利用生成的等时线的排列、疏密、弯曲形式、弯曲方向、延伸方向等参考条件,反向分析产生上述表象的可达性动因,发现暗藏于该区域道路网络内部的可达性规律。
2 等时线 2.1 等时线及其特性等时线是基于道路网络的可达性分析方法,用来表示从出发点出发,在经过相同的时空约束所有能到达的点的连线,等时区域则代表所有能到达的等时线内点的集合[18]。
等时线作为等值线的一种,拥有等值线的共性特征:①同一条等时线上的各点时间成本相同;②同一幅图中相邻两条等时线之间的时间差相等;③等时线是闭合的曲线;④等时线一般不相交、不重叠。等时线的疏密变化,弯曲变化以及延伸特性将在本文第4节详细介绍。
2.2 基于水流扩展思想的等时线生成方法本文提出一种基于水流扩展思想的等时线生成方法,通过道路网络栅格化实现矢量数据的离散化,操作对象的单元化;采用类似于水流扩展的算法模拟路径扩展过程,获取可达路径,扩展步长为权重约束函数控制的栅格单元长度;最后提取路径扩展终结点信息,通过基于凸包以及角平分线移位的方法确定等时区域边界。
2.2.1 道路网络栅格化
水流法首先对道路数据栅格化,类比遥感图像与像元的关系,对道路网进行栅格化处理,创建矢量数据中的基本分析单元。与传统的格网栅格化处理方式不同,定义道路交叉点和不同等级道路的分界点等特征点为网络节点,利用节点分割道路生成道路弧段,将道路网的每一条弧段都用相同的分割单元进行剖分,构造节点-弧段、栅格-栅格和节点-栅格拓扑关系,建立网络栅格数据结构。将对道路网进行的操作转变为对相关道路上的栅格单元进行操作,剖分效果如图 1(b)所示。
2.2.2 约束条件下的路径扩展过程将离出发点欧氏距离最近的栅格单元标记为新的发生元,初始化发生元。类比水滴沿木板的纹理扩散的过程,以发生元为“水源”,“水流”从发生元栅格出发,沿可扩展的方向扩展,扩展操作的执行路径只能是网络弧段。通过节点-栅格拓扑关系检索扩展栅格在可扩展方向上的邻接栅格,标记为新的扩展栅格。更新扩展栅格的位置及扩展边缘位置。遇到道路网络交叉口时,依据网络拓扑关系分散为不同支流继续扩展,如图 1(c)所示,在扩展时加入负载约束条件,设置权重约束函数,道路网上约束条件的变化直接反映为道路网剖分单元的变化,如图 2所示。单位时间扩展一个栅格步长,直至到达规定时间间隔或网络边终点。
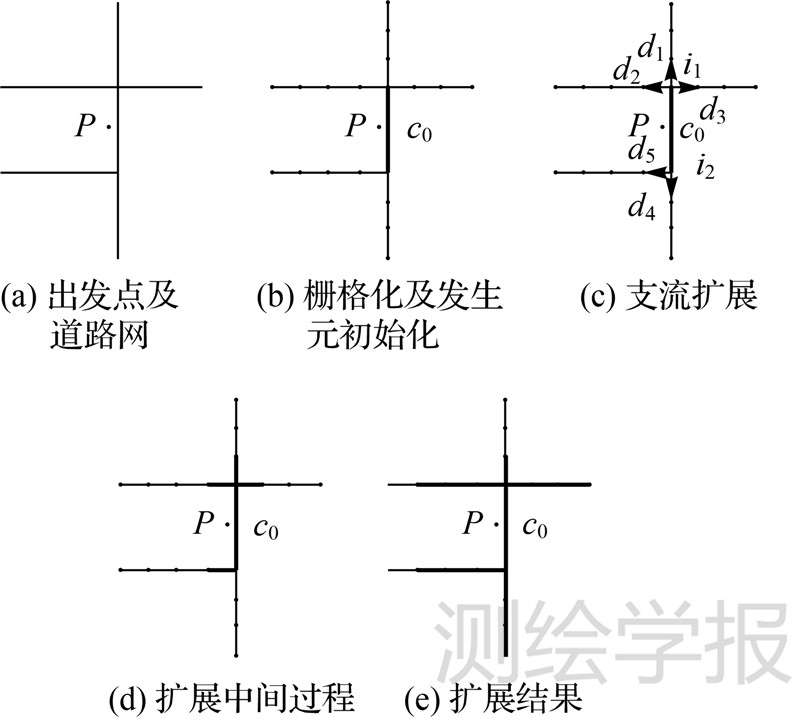
|
| 图 1 水流法扩展原理示意图 Fig. 1 Principle diagrams of the flow method |
|
| 图 2 基于水流法的等时线生成约束条件 Fig. 2 Constraints of generating isochrones based on the flow method |
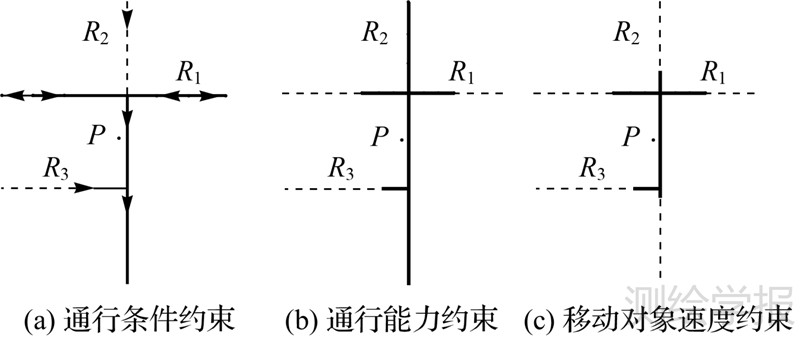
道路网拓扑结构以及交通流的变化会影响交通网络的可达时空范围,其原因是道路网约束了移动对象的运动范围,道路网上的交通状态也影响移动对象的运行速度,时空可达性的描述也应该跟用户的个性化需求及提供服务的设施数量密切相关[19]。道路网和个性化的需求必然会约束等时区域范围。等时线依托道路网获取可达路径时,需要考虑道路网本身的条件与限制、移动对象的属性及关心的时间分段。结合图 2,分析3类约束条件对扩展结果的影响:
(1) 道路网络约束:①道路通行条件约束,由于城市道路限制通行方向,在道路交叉口和出入口处判断道路在某方向是否通行,如图 2(a)所示,道路R2限制只能由北向南行驶,R3由西向东行驶,扩展4个单位时间的结果成“T”字型与图 1(e)形成对比,由此可得道路通行方向决定等时区域的排列;②道路通行能力约束:道路等级限制了等时范围,是影响等时区域形态的重要因素,图 2(b)中等级关系R2>R1>R3,设剖分栅格单元比4∶2∶1,扩展结果与图 1(e)对比发现路径向高等级道路方向延伸。
(2) 移动条件约束:移动对象的出行方式(步行或驾车)直接表现为移动对象的速度的变化,所以设置移动对象的速度权重,如图 2(c)所示,当移动对象速度减为原来的1/2时,扩展结果的规模减小。
(3) 时间分段约束:时间分段即所关心的时间间隔,如步行出行时适宜以较小的时间分段方式,5 min一个时间间隔。与移动对象速度约束的结果相似,时间分段将影响扩展结果的范围大小,此处省略示意图。
水流法可以在任意感兴趣的部分灵活加载约束条件,根据不同目的,选用不同的约束条件组合或在3类约束条件中定义新的扩展约束条件。如生成实时等时线图时,除了考虑道路通行条件约束和道路通行能力约束外,还需要考虑由交通拥堵约束,道路交叉口停滞约束。另外在地势起伏较大的区域,还应考虑地形约束。这方面的具体研究将在第3节试验部分给出实例。
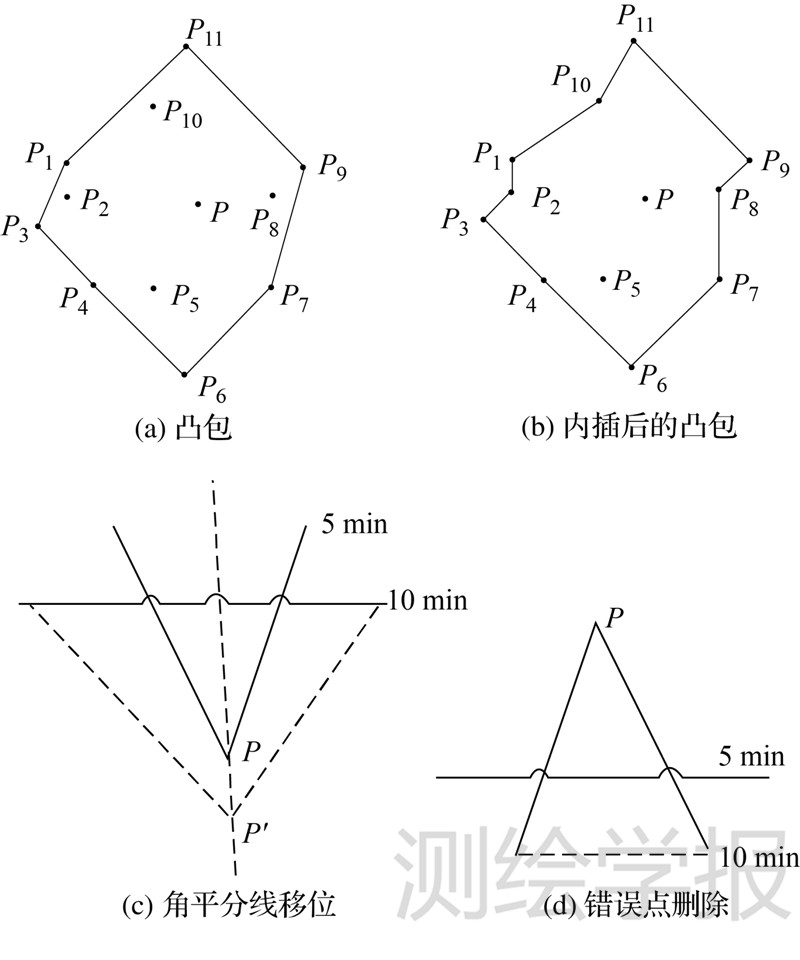
2.2.3 等时区域边界确定在水流扩展路径的基础上,提取所有扩展终点信息生成包含所有节点的最小凸多边形。利用凸包算法生成的等时线不能准确表达可达区域,将大量空白区域包括进来,产生较大误差,本研究在基础的凸包算法上进行扩展,当凸包内的点投影在距其最近的边上的投影距离小于阈值(本文设为一个单元栅格步长,即不加约束权重时的栅格步长)时,则将该点作为相应边的内插点进行内插,如图 3(a)、(b)所示。
|
| 图 3 等时区域边界确定 Fig. 3 Isochrones’ boundary determination |
由此生成的等时线在某些区域存在明显相交现象,产生相交的原因是断头路的存在使得后一圈生成的等时线在断头路区域扩展范围要小于前一圈的等时区域范围。等时线的弯曲通常是出现在道路上,考虑到计算道路方向的复杂度,取每一个弯曲的角平分线方向逼近道路方向,提出角平分线移位的解决方法,这样可以在形态上延续等时线扩展趋势,便于之后的分析并消除交叉。原则上不改变已经生成的等时线,原因是改变已经生成的等时线从几何意义上会导致连带反应,会造成5 min的可达范围和10 min内的5 min可达范围不一致的不合理情况。设定以下规则,如图 3(c)、(d)所示:
(1) 当5 min线上的点出现在新生成的10 min线外时,取该点与相邻结点组成的夹角的角平分线方向向外扩展阈值距离。
(2) 当10 min线上的点出现在5 min线内时,则将其视作错误点删除。
3 等时线生成试验本文基于domap软件系统开发了基于水流扩展思想的等时线生成功能模块,在i5-2640 m/2.8 GHZ/4 G/Windows7环境下,基于1∶10 000深圳道路网数据某区域内某固定点位置进行等时线生成模拟,该区域道路网数据包含5063条路段,参考《公路路线设计规范》按照道路等级主要分为城际道路80 km/h、快速路60 km/h、主干道50 km/h、次干道40 km/h以及支线20 km/h[20],道路等级权重分别设为8、6、5、4、2,并考虑方向限制。
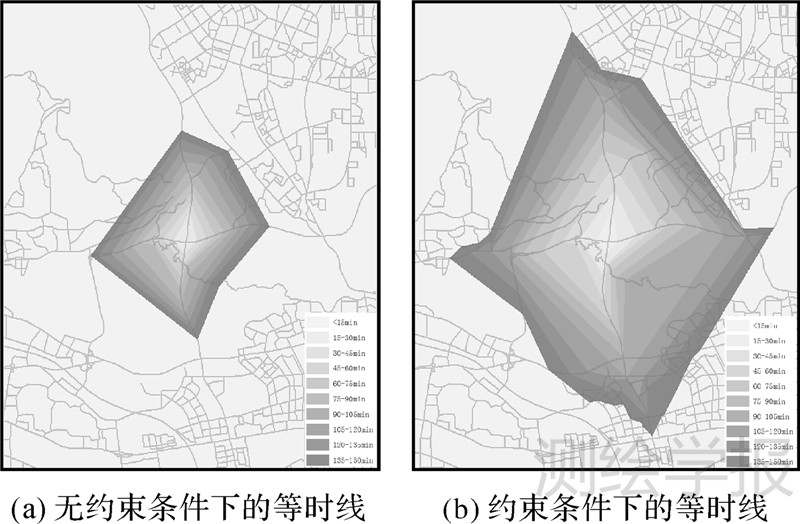
在深圳市1∶1万的道路网络下,设计了试验1,分别生成约束条件下和无约束条件下等时线,如图 4。
|
| 图 4 约束条件下的等时线和无约束条件下的等时线 Fig. 4 Isochrones with constraints and isochrones without constraints |
第2节中图 1和图 2分别展示了有/无约束条件下的栅格扩展路径的变化。现选取一组实际路网,呈现无约束等时线和约束条件下的等时线在实际路网中的不同延伸形态。试验1:设定无约束条件下的路网速度均设为10 km/h,道路权重均为1,此时的等时线沿道路网各方向均匀扩展,生成的等时区域形状规则,主要受道路网本身的拓扑结构影响。考虑道路等级约束条件及方向约束下生成的等时线在扩展范围和形状上都与无约束条件下的等时线有较大变化,更贴近实际情况。
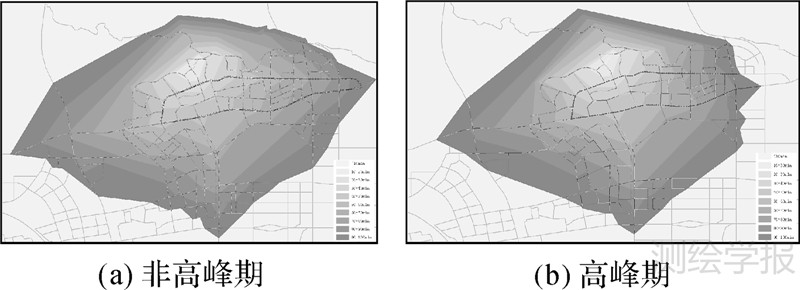
水流法负载约束的灵活性使得该算法与实时交通信息的结合成为可能。试验2:根据所获得的实时路况信息,可以选择性的在某个路段或区域,设置交通拥堵约束,实现实时等时线的制作。本研究主要是针对等时线生成方法,由于获取实时数据成本较高,本文采用高峰期和非高峰期两个敏感时间段作试验。在进行实时等时线的生成时,不仅需要考虑由于车流量增大而造成的行驶过程中的拥堵延误,道路交叉口及出入口处的信号灯也会引起等待及排队延误时间也不容忽视。因此为了更加贴近实际情况,在道路交叉口附近设置交叉口停滞约束条件,到达以交叉口为端点的栅格时设置停滞,本文假定停滞时间为一个信号灯周期60 s,即扩展到该类型的栅格时,其他栅格继续扩展,而该类型的栅格停滞扩展直至停滞时间到达60 s。
选取深圳市梅林关作为试验区域,梅林关及梅观路,进出关早晚高峰潮汐特点明显。高峰期会出现交通拥堵现象,因此在相关路段的行驶速度会受到限制,考虑交通拥堵约束及交叉口停滞约束,可以得到实时的等时线,如图 5所示(对梅林路和北环大道设置非高峰期速度40 km/h、50 km/h,高峰期速度20 km/h、30 km/h)。图 5(a)和图 5(b)中黑线为梅林路及北环大道处,对两处道路的剖分栅格进行夸张显示。对比两幅图中线框内部分,可以发现在相同的路段上,非高峰期的栅格单元比高峰期的栅格单元要长,高峰期栅格加密,并且等时线扩展范围在拥堵方向上被压缩,可以看出道路的拥堵加大了通行难度,限制了通行范围。
|
| 图 5 实时等时线 Fig. 5 Real-time isochrones |
道路的拥堵程度直接影响行驶速度,而地形作为道路的自然区位条件影响实际的可达范围。对于地势起伏较大的区域,只简单地计算二维平面的扩展距离并不能反映真实的情况。试验3:采用30 m分辨率的DEM影像内插出高程信息,将高程信息与道路网叠加,得到2.5维的道路网数据,设定地形约束函数,生成的等时线如图 6所示。图 6中等时线图与图 5(a)相比,南北方向相对其他方向地势起伏较大,等时区域在该方向上压缩明显。

|
| 图 6 地形约束下的等时线 Fig. 6 Isochrones with constraints of terrain |
本文利用第2节所述方法生成的等时线,针对等时线的形态特征设定指标,分析各指标的性质,对不同通行条件下的区域生成等时线,通过分析其形态特征发现可达性规律与道路网络特征的关系。各指标的性质及意义如表 1所示。
| 指标 | 性质 |
| 等时线的长度L | 表征扩展形状的边界大小的量 |
| 等时线的面积S | 表征扩展范围大小的量,值越大,范围越大 |
| 圆形度 | 取值范围为[0, 1],在相同面积的情况下,具有光滑边界的形状边界较短,圆形度较大,随着边界凹凸变化程度的增加,周长L相应增加圆形度减小。表征各项扩展均匀度的量,值越接近于1,越均匀 |
| 等时线时间坡度 | 表征等时线分布疏密的量,在相同的时间间隔下,当D逐渐变小,表示等时线由密集变稀疏,扩展能力由弱变强,反之亦然 |
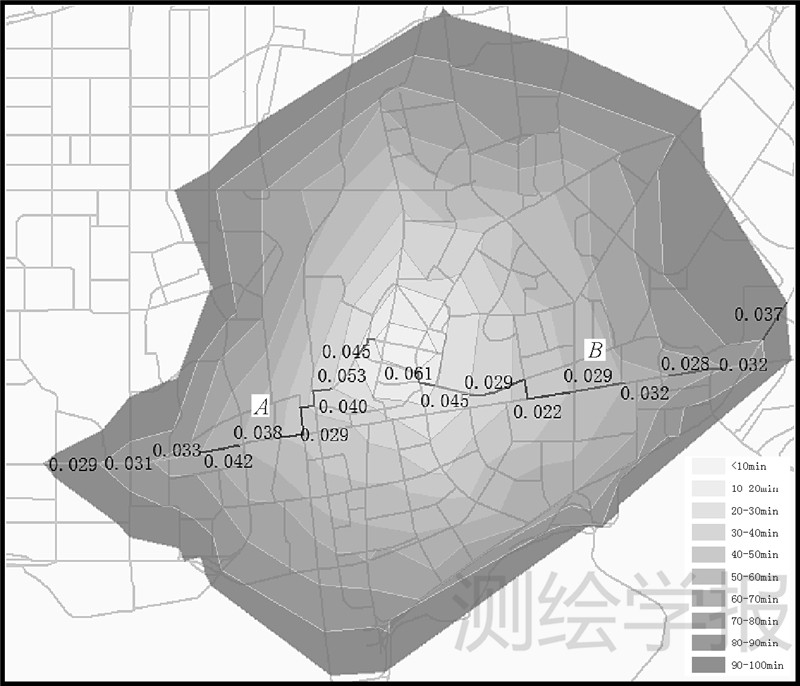
等时线的疏密变化通过时间坡度来衡量,网络空间下衡量时间坡度,需要沿道路方向,如图 7所示,在A、B两个方向上,坡度变化总体上均呈逐渐变小的趋势,等时线在该方向上分布由密集变为稀疏。等时线形态呈先圆滑后向某个方向扩展的趋势,A、B方向上相同时间间隔内沿道路网扩展的距离逐渐增大,扩展能力由弱变强,可达性差异变大。该区域为罗湖区的商业中心区,该区域道路应该分为两部分,内部道路和内外衔接道路,不仅内部需要有便捷的交通运输条件,还要有干线与外界道路连接。该区域中次干道纵横交错形成区域内部道路网骨架,为较为规则的网格结构,相邻次干道之间均有多条支路链接。区域与外界连接处包围有笋岗东路—文锦中路—深南东路—红岭中路—爱国路等多条主干道,使得该区域与外界交流便利,通达条件优越。
|
| 图 7 等时线疏密变化与时间坡度D Fig. 7 Isochrones’ density variation and time gradient D |
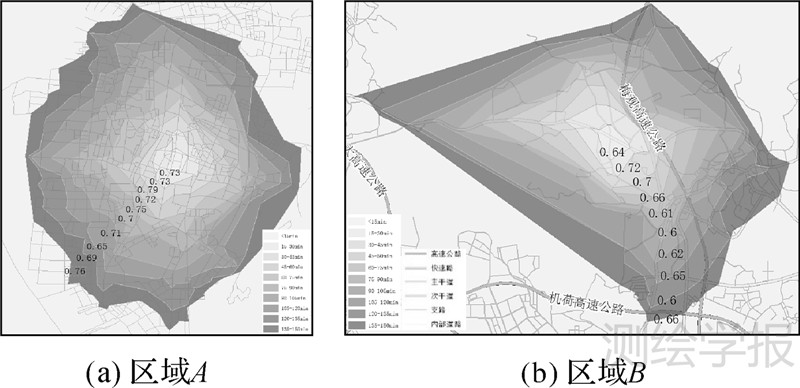
利用圆形度来衡量等时线各向可达性的差异,如图 8所示,选取深圳市道路网中不同道路密度的A、B两块区域,分别生成时间间隔为0.25 h的等时线。A区域中等时线边界圆形度较B区域较高,从等时线形态上看A区域也较B区域圆滑,这与区域内道路密度及道路级配有关,A区域等时线向各向扩展,等时线轮廓圆滑且形状饱满;B区域出现轴化扩展的形态,等时线轮廓平直,轴线方向上出现较大凸起弯曲,该方向上道路等级高于周边地区且差异较大,可达性扩展不平衡。等时线的弯曲变化表征等时线扩展的均匀度,等时线弯曲凸出或凹进处,表示该处的可达性比周边值较高或较低,且凹凸弯曲度越大,表示变化越大。
|
| 图 8 等时线弯曲变化与圆形度C Fig. 8 Isochrones’ bending variation and circularity C |
图 8(b)中的区域有纵向的梅观高速公路及主干道四黎路,横向的主干道观光路,周围搭配多条次干道及支路。从图 8中可以看出,生成等时线的多边形轴向延展方向与道路分级主方向一致,即等时线以高等级道路为轴线向外扩展延伸。图中横向轴线以北的等时线弯曲凹凸程度小于轴线以南的凹凸程度,这是由于北方向上主干道旁多为次干道,道路网络上可达性相对均匀,而南方向上多为支路,道路间级差较大,道路网络上可达性参差不齐,导致生成的等时线扩展力度不均,由此勾画出的等时线有较明显的凹凸起伏,这表明等时线弯曲的凹凸程度越大,则主方向上的道路级别与周边道路差异越大。
5 结 论作为道路网络可达性测度的一种工具,本文围绕等时线从概念、定义、生成方法及形态特征4个方面进行了讨论。对网络栅格化模型进行改进,提出了基于水流扩展思想的等时线生成方法,构建道路网络状况、移动条件和时间分段等约束条件下生成等时线。该算法可扩展性强,可以根据具体问题灵活地添加约束条件,很好地解决实时等时线和个性化等时线的生成问题。
类比等高线形态反映地势起伏特征,引入等时线形态分析,不仅可以反映时间序列上的可达性,还与道路网络结构内在特征联系紧密,不同区域的等时线均表现出各自特有的形态:①等时线的疏密可以反映可达性的地区差异;②等时线弯曲凸出或凹进处,表示该处的可达性比周边值较高或较低,且凹凸弯曲度越大,表示变化越大;③等时线的延伸方向与高等级的道路有较强的一致性;④等时线弯曲平滑(圆形度越高)表示等时区域内各向可达性较均匀,差异较小,反之亦然。
后续需要扩展研究的内容有以下3点:①结合公交线路等实际的离散型时间表数据扩展算法,多模态联运网络下的等时线的生成可以分为在时间和空间上分别离散和连续的模态,结合公交站点数据,设置水流扩展断点,标记流经的公交站点,实现分段处理;②结合数据处理和数据挖掘的相关理论,与数据部门取得合作,获得实时交通数据,开发相应的客户端应用程序,以生成等时线;③对更多的道路网络类型进行等时线分析验证,如重庆枝状自由式网络、西安方格网式网络、成都环形放射式网络、北京混合式网络等。
| [1] | POOLER J A. The Use of Spatial Separation in the Measurement of Transportation Accessibility [J]. Transportation Research Part A, 1995, 29(3):421-427. |
| [2] | SHEN Q. Spatial Technologies, Accessibility and the Social Construction of Urban Space [J]. Computers, Environment and Urban Systems, 1998, 22 (5):447-464. |
| [3] | MILLER H J. Modeling Accessibility Using Space-Time Prism Concepts within Geographical Information Systems [J]. International Journal of Geographical Information System, 1991, 5:287-301. |
| [4] | KWAN M P. Space-time and Integral Measures of Individual Accessibility: a Comparative Analysis Using a Point- Based Framework [J]. Geographical Analysis, 1998, 30: 370-394. |
| [5] | KIM H M, KWAN M P. Space-time Accessibility Measures: A Geocomputational Algorithm with a Focus on the Feasible Opportunity Set and Possible Activity Duration [J]. Journal of Geographical Systems, 2003, 5(1): 71-91. |
| [6] | HGERSTRAND T. What about People in Regional Science [J]. Papers of the Regional Science Association, 1970 (24):7-21. |
| [7] | O’SULLIVAN D, MORRISON A, SHEARER J. Using Desktop GIS for the Investigation of Accessibility by Public Transport: An Isochrone Approach [J]. International Journal of Geographic Information Science, 2000, 14(1):85-104. |
| [8] | JULII S B, ANDREW A L, IAN J B. Using Isochrone Surfaces in Travel-Cost Models [J]. Journal of Transport Geography, 1997, 5(2):117-126. |
| [9] | FORER P C, KIVELL H. Space-time Budgets, Public Transport, and Spatial Choice [J]. Environment and Planning A, 1981, 13: 497-509. |
| [10] | LIGHTFOOT C, STEINBERG T. MySociety: Travel-time Maps and Their Uses [EB/OL]. [2006-03-04]. http://www.mysociety.org/2006/travel-time-maps/. |
| [11] | JIANG B. A Short Note on Data-Intensive Geospatial Computing [M]//Information Fusion and Geographic Information Systems. Berlin: Springer Berlin Heidelberg, 2011: 13-17. |
| [12] | STREET N. TimeContours: Using Isochrone Visualisation to Describe Transport Network Travel Cost [R].London:Imperial College London,2006. |
| [13] | BAUER V, GAMPER J, LOPERFIDO R, et al. Computing Isochrones in Multi-Modal, Schedule-Based Transport Networks [C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. [S.l.]:ACM, 2008: 78. |
| [14] | MARCIUSKA S, GAMPER J. Determining Objects within Isochrones in Spatial Network Databases [C]//Proceedings of Advances in Databases and Information Systems. Berlin:Springer Berlin Heidelberg, 2011: 392-405. |
| [15] | GAMPER J, BHLEN M, COMETTI W, et al. Defining Isochrones in Multimodal Spatial Networks [C]//Proceedings of the 20th ACM International Conference on Information and Knowledge Management. [S.l.]:ACM, 2011: 2381-2384. |
| [16] | GAMPER J, BHLEN M H, INNEREBNER M. Scalable Computation of Isochrones with Network Expiration[C] //Proceedings of Scientific and Statistical Database Management. Berlin:Springer Berlin Heidelberg,2012: 526-543. |
| [17] | DIJKSTRA E W. A Note on Two Problems in Connexion with Graphs [J]. Numerische Mathematik, 1959, 1(1): 269-271. |
| [18] | DOLING J. Accessibility and Strategic Planning [M]. Birmingham: University of Birmingham,1979. |
| [19] | FANG Zhixiang, LI Qingquan, SHAW Shilun. Representation of Location-specific Space-time Accessibility Based on Time Geography Framework [J]. Geomatics and Information Science of Wuhan University, 2010, 35(9): 1091-1095.(方志祥, 李清泉, 萧世伦.利用时间地理进行位置相关的时空可达性表达[J].武汉大学学报:信息科学版. 2010, 35(9):1091-1095.) |
| [20] | Ministry of Communications of the People’s Republic of China. Specification for Design of Highway Route JTG D20—2006 [S].Beijing: Standard Press,2006. (中华人民共和国交通部.公路路线设计规范JTG D20—2006 [S].北京:标准出版社, 2006.) |



