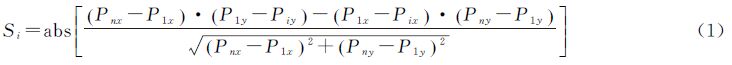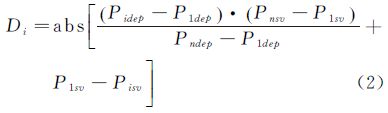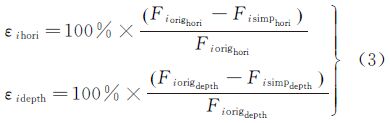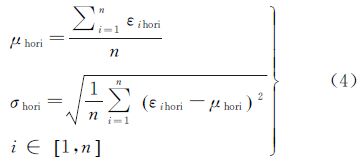2. 国家海洋局海底科学重点实验室,浙江 杭州 310012
2. Key Laboratory of Submarine Geosciences,State Oceanic Administration,Hangzhou 310012,China
1 引 言
多波束测深系统自20世纪90年代引进我国以来,已被广泛应用。目前,关于多波束数据误差分析和数据处理已取得较多的研究成果[1, 2, 3, 4, 5, 6, 7]。多波束系统采用定向发射一组声波,接收其双程反射或散射时间,并通过声速剖面(sound velocity profile,SVP)结构,基于斯涅尔定律计算探测目标的水深和坐标[8]。声速剖面一般通过直接法(仪器测定)和间接法(声速经验模型)确定[9]。目前,声速剖面测量设备(如AML公司的SV PLUS)的采样率普遍可达到20 Hz[10],如果按1 m/s的仪器下降速度算,100 m水深所采集的声速剖面数据点的数量将达到2000组。在深水区进行多波束勘测,SVP数据量将非常庞大。高采样密度的声速剖面数据,导致射线追踪与波束脚印归算的运算时间大幅增加,从而降低了多波束勘测工作效率,有时甚至导致多波束系统不能正常运行。很多多波束测深系统对所使用SVP的数量提出了限制,如,最早引进我国的深水多波束系统SeaBeam 2112就限制声速剖面数据文件中声速数据不超过30行[11];又如,Kongsberg EM系列多波束系统对输入处理单元用于实时射线追踪计算的SVP文件进行限制,要求声速剖面文件不能大于30 kB,对于EM710、EM302和 EM 122,最大采用数据点数量不超过1000组,对于更老型号的系统,则不超过570组[12]。为了提升多波束勘测与数据处理的时效性,必须筛除原始声速剖面中的冗余点,同时需要评估和控制精简后的声速剖面所带来的误差。
在多波束勘测过程中,多采取人工方法挑选声速剖面特征点,但人工方法挑选的SVP精度难以评估,易遗漏SVP的特征点,同时效率也非常低。文献[13]提出了新的方法,通过选定一定深度值大小的窗口,对声速数据进行滑动平均后,将所求的平均声速值作为窗口中心位置深度所对应的声速值,但此方法可能会遗漏原始声速剖面的特征点。在多波束数据后处理中,近年来发展了一种基于等效声速模型的改正方法,文献[14, 15, 16, 17, 18]先后提出了多种等效声速模型或改进方法,有些模型已在假地形数据改正处理中得到很好的应用[14, 15, 16]。但等效声速方法完全抛弃了实测声速剖面数据,易导致在水深变化剧烈的复杂海底地形区改正效果不佳,同时由于多波束测深误差的复杂性和多源性,该方法也易掩盖其他非声速剖面造成的误差。因此,既要精简声速剖面以提升工作效率,又要忠实原始声速剖面以避免对多波束实测数据误差多来源的掩盖是值得深入研究的问题。
为解决原始声速剖面快速精简问题,本文提出了基于声速最大偏移量法(maximum offset of sound velocity,MOV)的SVP精简与评估方法。该方法建立在实测声速剖面数据基础上,对D-P(Douglas-Peucker)算法进行改进,通过计算声速维度上的最大距离,判断声速采样点的取舍,完成精简声速剖面数据的处理。为了评估精简后的声速剖面的精度,基于实测声速剖面,采用射线追踪法和误差百分比分析法评估精简前后的声速剖面对测深精度的影响。经过此算法处理后的声速剖面,不仅能够保证射线追踪后的波束脚印精度,还能大幅减少计算时间,有效地提升外业调查和内业数据处理的工作效率,在工程应用上具有重要的实际应用价值。
2 试验数据声速剖面采集仪器为加拿大RBR公司生产的XR-420型温盐深仪,该仪器采样率为1 Hz,温度范围-5°C-35°C,精度0.002°C、电导范围0-85 ms/cm,精度0.003 ms/cm(35 psu 15°C)、深度范围为500 m,精度为满量程的0.05%,使用威尔逊(Wilson)经验公式计算声速。
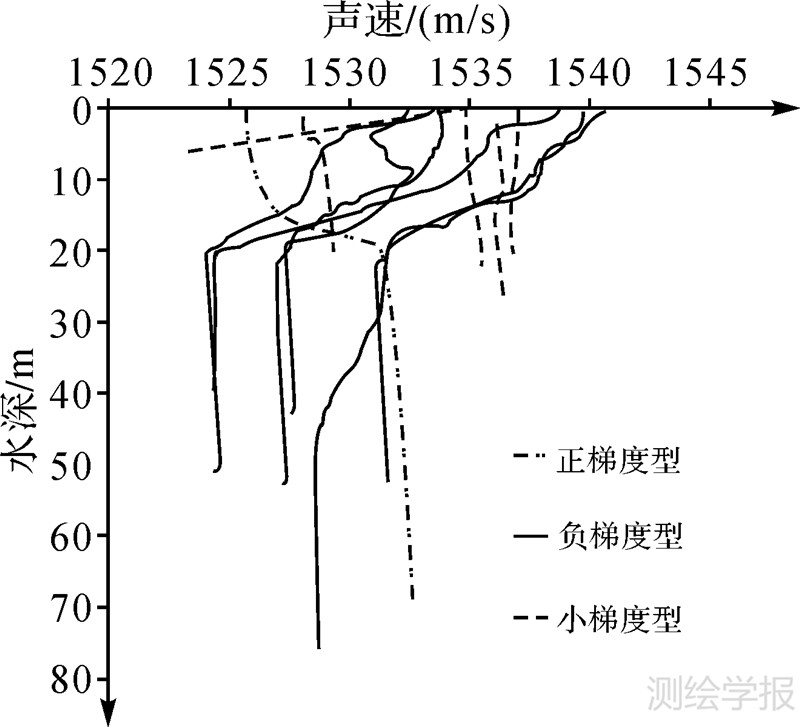
2012年7-8月,在执行多波束勘测任务过程中,于台湾海峡北部区域使用XR-420型温盐深仪实测声速剖面11个(图 1)。对获取的11个声速剖面数据进行分析与分类,可分为3种类型(图 1):①正梯度型,声速随深度的增加而增大;②负梯度型,声速随深度的增加而减少;③小梯度型,声速随深度的增加而几乎不变。从图 1中可以看出该区域的声速的基本特征:①区域声速变化范围在1523~1541 m/s,在不到100 m水深的垂向范围内声速变化达18 m/s,表明该区水文环境复杂,声速变化剧烈;②多数声速剖面在3.5 m和20 m左右出现两个明显的声速跃层,3.5 m的声速跃层可能系太阳光照和表层流引起,20 m的跃层可能属于两种不同性质的海流在海峡混合导致;③该区域的声速剖面类型主要为负梯度型构成,这与多数海域的声速剖面不同;④经查证勘测日志,小梯度型声速剖面是由于台风过境后所导致的海洋水团充分混合,从而使声速在垂向上的分层特征消失。
|
| 图 1 实测声速剖面数据 Fig. 1 Measured sound speed profile data |
为验证本文方法的有效性,还使用了同步测量的多波束测深数据,并使用精简前后的声速剖面进行了多波束水深数据处理的时效对比分析。
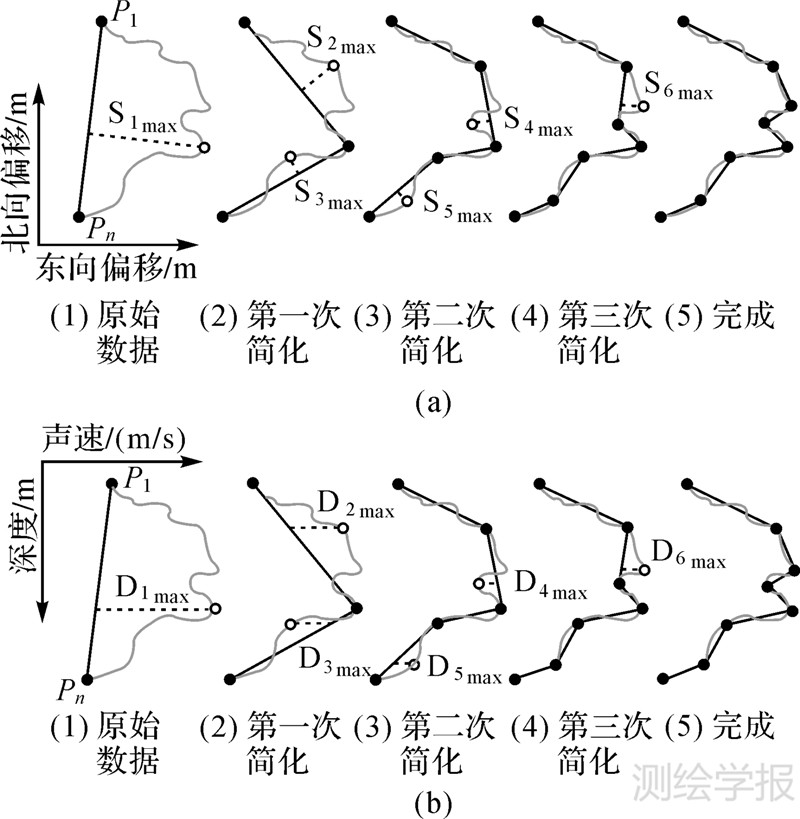
3 方法与模块 3.1 改进的D-P算法 3.1.1 D-P算法D-P线简化算法是一种用于计算机图形显示方面,对高度复杂的多段线对象进行线简化的常用方法[19]。该算法的基本思想,如图 2(a)所示,首先确定该算法的唯一参数阈值Q(单位为m),连接线段首尾两个端点P1和Pn,依次计算线段内其余各点Pi到这条直线的垂直距离Si,找出其中最大垂直距离Simax,比较Q和Simax的大小,Si计算公式为
若Simax≤Q,则删除首尾两点以外的所有点,结束;若Simax>Q,则保留此点Pi,从Pi处将线段分为两个部分;分别连接P1和Pi以及Pi和Pn,同式(1)对这两段重复计算垂距,检查最大垂直距离Sjmax和Skmax是否大于Q;重复迭代上述过程,直到所有点到线段的垂直距离Si≤Q,完成线简化运算。
|
| 图 2 改进前后的D-P算法示意图 Fig. 2 A comparison of D-P algorithm before and after the improvement |
D-P算法是为两个坐标轴上单位相同的二维线性对象简化所设计的,但对于声速剖面数据,其横坐标代表声速,单位为m/s,纵坐标为深度,单位为m。在该种情况下,D-P算法所依赖的基本物理模型与数学模型已经发生变化,无法计算距离,不可直接用于SVP的精简。
本文在D-P算法的基础上进行了改进,由距离计算改变为声速维的最大偏移量计算。如图 2(b)所示,对于给定的阈值参数T(单位为m/s),连接剖面首尾两个数据点P1和Pn,依次计算线段内其余各点Pi到这条直线在声速维度上的距离Di,找出最大距离Dimax,比较T和Dimax的大小,Di计算公式为
其余步骤同上所述的D-P算法,直到没有多余的点被舍弃,完成声速剖面数据的精简。该方法中阈值参数T的智能选取是关键步骤。
因此,本文所改进的D-P算法适用于二维坐标系不同维度的曲线简化,就SVP精简而言,可称之为声速最大偏移量法。显然这种方法可扩展到其他类似的二维曲线简化问题。
3.2 方法基本模块构成如何判断精简后的SVP是否符合精度要求?因此,本文的研究可分解为两个问题:SVP的精简问题,以及精简后的SVP对于多波束测深及数据处理精度的分析问题。基于此,该方法可分解为两大模块:精简模块和评估模块(图 3)。

|
| 图 3 MOV法基本模块 Fig. 3 Basic models of MOV method |
精简模块用于声速剖面的精简,其核心是上文所述的MOV算法,其主要实现步骤如下。
(1) 数据输入:输入原始声速剖面点数据集Vorig和阈值参数T。
(2) 变量初始化:初始化存储精简声速剖面点数据集的变量Vsimp和其他变量。
(3) 提取声速最大偏移:使用循环算法和式(2)获取最大偏移量值Dmax和所对应的声速点数据Pk。
(4) 剖面线段切割:判断Dmax和T的大小,若Dmax≤T,转至步骤(5);若Dmax>T,保存Pk至Vsimp,将剖面线段在Pk处分为两段,并分别返回步骤(3)。
(5)数据输出:将Vorig中起始和终止声速点数据保存到Vsimp,并输出Vorig和Vsimp。
3.2.2评估模块评估模块是用于评估精简前后的声速剖面对波束脚精度的影响,其核心是射线追踪法和误差分析法,该模块主要体现在以下三大步骤。
(1) 数据输入:输入原始声速剖面点数据集Vorig和精简声速剖面点数据集Vsimp。
(2) 射线追踪:使用循环算法和层内常梯度射线追踪算法,计算波束样本数据库中的波束Bi(i∈[1,n])在原始声速剖面Vorig下对应的脚印位置坐标Fiorig(i∈[1,n])和在精简声速剖面Vsimp下对应的脚印位置坐标Fisimp(i∈[1,n]);并计算其在水平位移方向的误差百分比εihori(i∈[1,n])和深度方向的误差百分比εidepth(i∈[1,n])。
(3) 精度评定:计算所有波束脚印在水平位移方向的平均误差百分比和方差百分比μhori、σhori以及在深度方向的平均误差百分比和方差百分比μdepth、σdepth。
(4) 数据输出:输出精简后的声速剖面Vsimp以及精度评估数据σhori和σdepth。
4 关键技术问题研究 4.1 阈值对SVP精简的影响及计算区间的自动搜索SVP精简问题的核心在于算法阈值的自动选择。为研究该问题,从实测的SVP数据集中任选一实测声速剖面,分析在不同阈值大小下,该算法对声速剖面的精简情况。
图 4中红色实线代表原始声速剖面,绿色实线代表精简后的声速剖面。当选取一个较小的阈值,如0.05 m/s时,精简后的声速剖面数据点数量从214个下降到21个,精简率达90.19%,原始和精简后声速剖面的相关系数为0.999 99,表明此时精简后的剖面能较好地保留原始剖面的主要特征。当阈值增大一倍,即0.1 m/s时,精简后的剖面数据点数减少了一半,精简率为94.86%,原始和精简后数据的相关系数为0.999 94,表明精简后剖面较好地保留了原始剖面的主要特征。随着阈值的继续增大,声速剖面数据点数量不断减少。当阈值为0.25 m/s时,精简剖面的点数又减少了3个,精简速度明显放缓,精简率为96.26%,相关系数相应地下降为0.999 92。当阈值取0.5 m/s时,算法对原始声速剖面数据的精简速率继续放缓,为97.66%,剖面底部被精简为一条直线,原始数据细节特征在快速消失,相关系数快速下降为0.999 04。当阈值增大到1.0 m/s时,原始剖面进一步精简为4个特征点,精简率为98.13%,相关系数为0.998 64。当阈值取3.0 m/s时,剖面精简率高达98.60%,相关系数急速下降为0.953 15,声速剖面被简化为二层水层模型,原始剖面特征已基本消失。试验中,随着阈值的继续增大,最终精简剖面将只保留原始剖面起点和终点,对应的最大剖面简化率为99.07%,相关系数减为最小的0.834 57。

|
| 图 4 不同阈值下声速剖面简化情况 Fig. 4 Cases of simplified SVP under different thresholds |
由此上述实例分析可以看出,阈值的选取对于声速剖面的精简和保真至关重要,见表 1。
| 阈值T/(m/s) | 原始剖面点数norig | 精简剖面点数nsimp | 精简率/(%) | 剖面相关系数r |
| 0.05 | 214 | 21 | 90.19 | 0.999 99 |
| 0.1 | 214 | 11 | 94.86 | 0.999 94 |
| 0.25 | 214 | 8 | 96.26 | 0.999 92 |
| 0.5 | 214 | 5 | 97.66 | 0.999 04 |
| 1 | 214 | 4 | 98.13 | 0.998 64 |
| 3 | 214 | 3 | 98.60 | 0.953 15 |
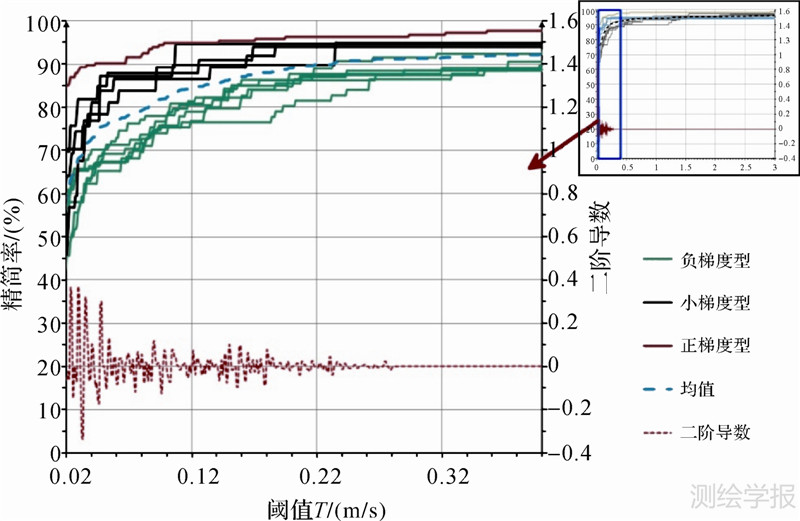
为进一步分析阈值对于声速剖面精简的影响,将实测的11个声速剖面按不同阈值进行精简处理,得到阈值和精简率的关系图。如图 5所示,该算法对所有类型的声速剖面都能较好地完成精简工作。在阈值取0.02 m/s时,该算法对剖面的平均精简率约为60%;在阈值取0.12 m/s时,该算法对剖面的平均精简率约为82%;在阈值取0.22 m/s时,算法对剖面的平均精简率约为90%,即100个数据点只保留10个;当阈值取0.50 m/s时,精简率约为93%,此后简化曲线逐渐趋向于平行;图中所有简化率曲线呈阶梯状上升,表明该算法对数据的精简是不连续的。当阈值超过某一个数值的时,简化率将不会继续增大,这个临界值,即剖面数据点精简为原始剖面的起点和终点,此时的简率为2/n(n为原始声速剖面点数)。
|
| 图 5 阈值vs声速剖面简化vs均值二阶导数 Fig. 5 The reduction rate and the second derivative plotted versus the threshold T |
图中红色实线对11个声速剖面精简率均值(图 5黑色虚线)的梯度再求导数,即二阶导数。当阈值为0.04 m/s时,二阶导数的值突然减小到0.1左右;当阈值为0.18 m/s时,此后的二阶导数的值逐渐趋近于零。由此可见,针对一个特定的SVP进行精简,其阈值存在一个区间[T1,T2],T1和T2就是SVP精简率梯度发生突变的位置。
4.2 精简后的SVP精度分析在精简后的SVP被使用之前,有两个问题必须理清,首先是精简后的声速剖面是否会影响最终声速折射改正,其次是阈值的大小与测深数据精度的关系。由于多波束系统是一个由众多子系统组成的复杂系统,其误差具有多源性,如果直接使用原始多波束数据,采用构建精简前后地形对比度方法进行评估难免会引入其他误差源。为了解决该问题,笔者使用误差百分比分析法评估精简后的声速剖面数据对水深数据精度所造成的影响。
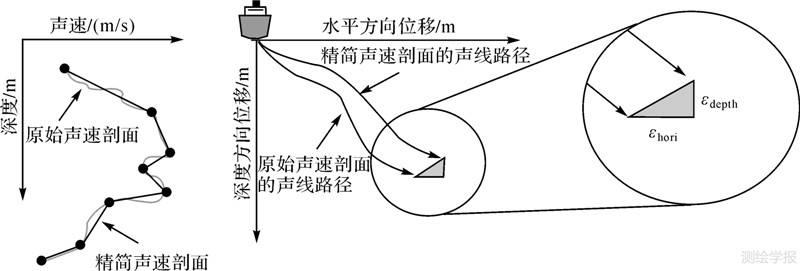
如图 6所示,为快捷评估声速剖面对于测深的影响,假设水深数据由水平位移方向的值和与其对应的深度方向的值构成,分别使用原始声速剖面和精简后的声速剖面,采用层内常梯度射线追踪算法对同一波束进行波束脚印归算对比,分析两个波束脚印在水平位移方向和垂直方向的误差百分比(假设原始声速剖面对应的波束脚印是正确的)。由于声速剖面的准确性对边缘波束的影响较大,为了消除入射角度对于水深误差的影响,本文所选波束样本库的波束,其入射角范围均在60°±1°范围内。对于某一确定的阈值,本方法的实现步骤如下:
(1) 从坐标原点出发的,分别使用原始声速剖面Vorig和精简后的声速剖面Vsimp,对波束样本库中同一波束Bi(i∈[1,n])进行射线跟踪,得到波束脚印Fiorig和Fisimp(i∈[1,n]);使用式(3),计算这两个脚印在水平位移方向和深度方向的误差百分比εihori和εidepth(i∈[1,n])
(2) 使用式(4)和式(5),计算该阈值下水平位移方向的平均误差百分比μhori、标准差百分比σhori以及深度方向的平均误差百分比μdepth、标准差百分比σdepth
|
| 图 6 误差百分比分析法示意图 Fig. 6 A sketch of percentage error analysis method |
表 2为对所有实测声速剖面在选取不同阈值精简后,产生的误差百分比均值统计的结果。由于阈值的增加导致不断精简的声速剖面,使得水深数据(水平位移方向和深度方向)的标准误差百分比不断增大。但水平位移方向和深度方向的平均误差百分比μhori和μdepth变化并不强烈,这是由于在大量数据统计的情况下,绝对值相同的正负平均误差百分比相互抵消的结果。当阈值为0.01 m/s或更小时,相应精简后的声速剖面进行波束脚归算几乎不产生任何水深标准差百分比。
| 阈值T/(m/s) | 简化率均值/(%) | 水平位移方向 | 深度方向 | |||
| μhori/(%) | σhori/(%) | μdepth/(%) | σdepth/(%) | |||
| 0.01 | 44.2 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.05 | 76.1 | 0.00 | 0.01 | 0.00 | 0.01 | |
| 0.1 | 82.1 | 0.00 | 0.02 | 0.00 | 0.02 | |
| 0.25 | 90.0 | 0.00 | 0.05 | 0.00 | 0.05 | |
| 0.5 | 93.4 | 0.00 | 0.10 | 0.00 | 0.10 | |
| 0.75 | 94.1 | 0.00 | 0.15 | 0.00 | 0.15 | |
| 1 | 94.3 | -0.01 | 0.20 | -0.01 | 0.19 | |
| 2 | 95.3 | 0.01 | 0. 41 | 0.01 | 0.43 | |
| 3 | 96.1 | 0.01 | 0.51 | 0.01 | 0.49 | |
| 4 | 96.2 | 0.02 | 0.6 | 0.02 | 0.61 | |
| 5 | 96.3 | 0.02 | 0.68 | 0.03 | 0.70 | |
| 6 | 96.4 | 0.03 | 0.75 | 0.03 | 0.76 | |
| 7 | 96.5 | 0.02 | 0.77 | 0.02 | 0.78 | |
| 8 | 96.5 | 0.02 | 0.77 | 0.02 | 0.78 | |
如表 2和图 7所示,当阈值T∈[0, 1]时,随着阈值的增大,阈值和水深数据的标准差百分比呈线性关系,其斜率为0.2;当阈值T∈[1, 7]时,随着阈值的增大,阈值和水深数据的标准差百分比呈非线性关系;当阈值大于7 m/s时,曲线的斜率为零,此时,SVP已经简化为首尾两点的最简化模型。

|
| 图 7 阈值vs水深标准误差百分比 Fig. 7 The standard deviation percentage error σ plotted versus the threshold T |
国际海道测量组织(International Hydrographic Organization,IHO)对水深测量的标准为:水深大于30 m时,水深误差百分比必须控制在1%以内,但是在实际测量情况下,只有0.3%~0.5%的水深误差百分比可以被分配给声速剖面折射误差和波束指向角误差[20]。上述试验证明随着阈值的增大(图 7),剖面不断精简,但也导致水深误差百分比随之增大,因此SVP的精简必须要符合一定的要求。基于此,根据试验结果,本文建议对于SVP误差所带来的水深误差百分比可控制在0.1%,并以此为标准来精简原始SVP。
4.3 声速剖面自动精简与寻优通过上述分析,可知SVP精简和评估是两个有密切联系的算法过程。由精简模块产生一个精简后的SVP,然后由评估模块进行评估,以判断是否符合精度要求,如此往复,直至获取满足要求的SVP。但如何对方法的核心参量阈值进行限定和自动筛选是降低运算量的关键。
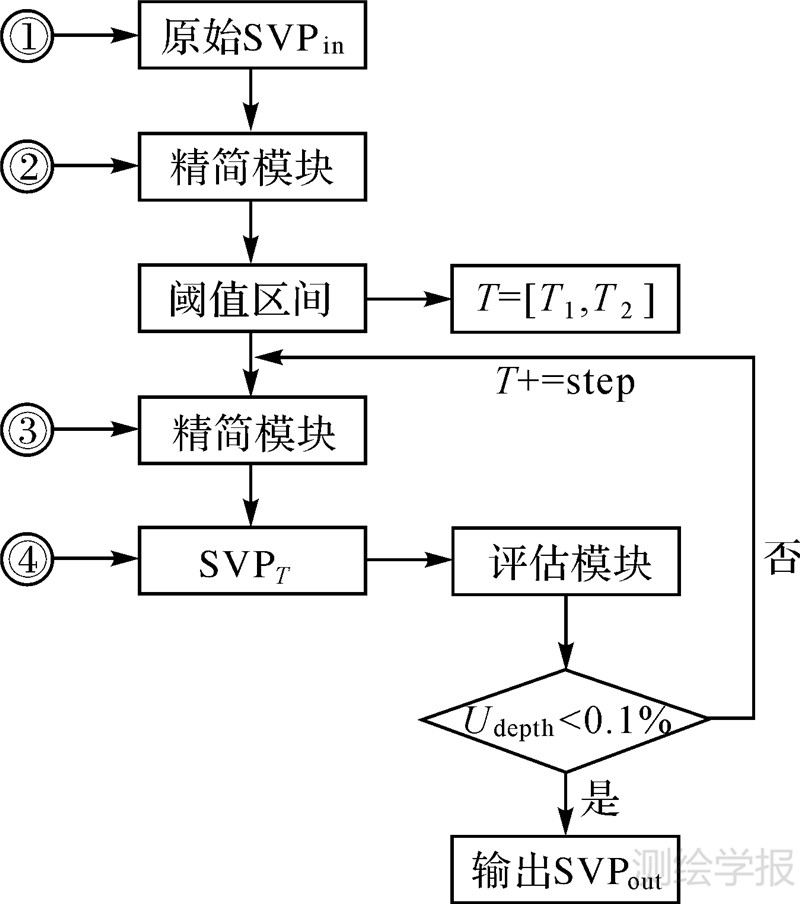
基于上述考虑,提出如下SVP自动精简与评估流程(图 8):①输入原始的SVPin;②调入精简模块,通过D-P算法获取阈值T的区间[T1,T2],设置阈值T的初始值为T1,该步骤的目的在于减少程序运算量,将阈值的计算范围进行限定;③再次调入精简模块,根据阈值T计算一个中间结果的SVPT;④调入评估模块,导入SVPT,使用射线法评估水深标准差百分比σdepth是否小于0.1%,满足则输出结果,否则按步长step自动调整T,并返回步骤③,直至计算出符合要求的SVPout;计算步长值step可由外部输入,也可由程序自动根据阈值区间计算。
|
| 图 8 声速剖面自动寻优过程 Fig. 8 The flow diagram of SVP automatic optimization |
该流程以阈值的自动选取为纽带,将精简模块与评估模块结合在一起,最终自动实现实测SVP的自动寻优过程。
5 实例时效分析为了检验精简前后的声速剖面对数据处理效率的影响,基于实测的多波束测深数据,使用精简前后的SVP进行数据处理对比,以进行时效分析。
参与试验的多波束探测设备为SeaBeam 1180多波束测深系统,采集区域位于台湾海峡北部,所采集的水深区间为40~50 m。共选取了40个数据文件,测线长度为498 km,数据量为390 MB,原始数据点数(Beam)为5.83×106个。
参与试验的声速剖面来自多波束勘测同步测量(图 1),本文从3种类型的声速剖面中各选取1个声速剖面,按不同阈值大小,以水深标准误差百分比σdepth小于0.1%为条件进行精简,获得精简后的声速剖面。
参与试验的多波束处理软件为Caris HIPS 7.1,使用该软件中的声速改正模块对不同声速剖面数据进行声线追踪[21],并统计运算时间。
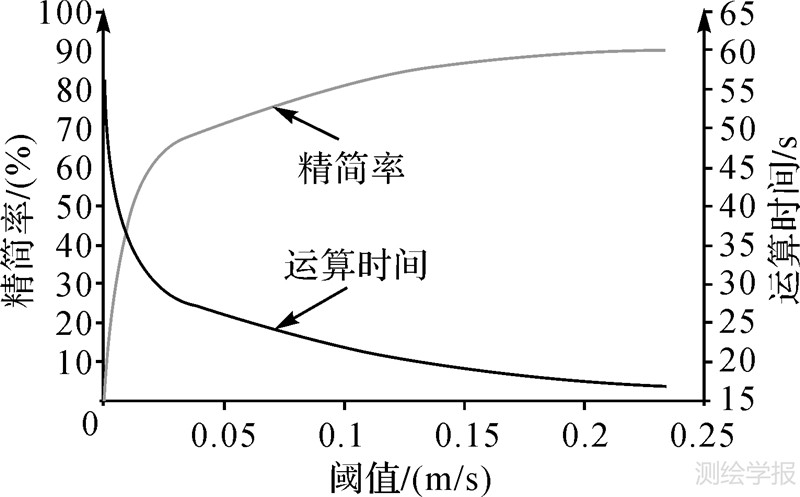
如图 9所示,当阈值为0,即使用原始声速剖面时,声线追踪所需的时间为58 s;随着阈值的不断增大,剖面精简率的不断提高,相应声线追踪所需的时间不断减少,且呈现非线性下降的趋势;当精简率为90%时,声线追踪所需的时间为17 s。
|
| 图 9 阈值与精简率和运算时间关系 Fig. 9 The relation of threshold and operation time |
由此可见,使用本文方法所精简的声速剖面在保证数据精度的前提下,能大幅减少数据后处理的运算时间,当精简率为90%时,数据处理的工作效率提升了3.41倍,工作效率显著提升,表明本文方法对于多波束探测与数据处理具有重要的工程应用价值。
6 结 论(1) 提出并实现了一种适用于实测声速剖面数据的精简运算的MOV方法。该算法是一个基于整体考虑的简化算法,可保留声速剖面上较大弯曲形态上的特征点。
(2) 给出了实测声速剖面精简的详细流程与方法。为评估精简后的声速剖面对于测深精度的影响,进而采用射线追踪法分析不同阈值对于测深与垂直航迹方向距离的影响,结果表明阈值大小与误差基本呈线性关系。
(3) 基于实测数据的分析表明,使用MOV方法对声速剖面数据进行精简,通过自动优选阈值,可减少原始声速剖面90%的数据点,由此引入的水深不确定度可控制在0.1%以内。
(4) 基于实测多波束数据的对比处理试验表明,通过实测速剖面的自动精简与优选,可大幅提升多波束勘测与数据后处理的工作效率,也表明所研究方法具有重要的工程应用价值。
| [1] | YANG Fanlin, LI Jiabiao, WU Ziyin,et al.The Methods of High Quality Post Processing for Shallow Multibeam Data[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(4): 444-457.(阳凡林, 李家彪, 吴自银, 等.浅水多波束勘测数据精细处理方法[J].测绘学报,2008,37(4): 444-457.) |
| [2] | YANG Fanlin, LI Jiabiao, WU Ziyin,et al.The Methods of Removing Instantaneous Attitude Errors for Multibeam Bathymetry Data[J].Acta Geodaetica et Cartographica Sinica, 2009,38(5):450-456.(阳凡林, 李家彪, 吴自银, 等.多波束测深瞬时姿态误差的改正方法[J].测绘学报, 2009,38(5):450-456.) |
| [3] | ZHANG Hongmei, ZHAO Jianhu.Quality Control of GPS Height in Precise MBS Measurement[J].Acta Geodaetica et Cartographica Sinica, 2009,38(1):22-27.(张红梅, 赵建虎.精密多波束测量中GPS高程误差的综合修正法[J].测绘学报,2009,38(1):22-27.) |
| [4] | HUANG Xianyuan, ZHAI Guojun, SUI Lifen,et al.The Influence of Optimized TRA in Samples on Elimination of Sounding Outliers in the LS-SVM Arithmetic[J].Acta Geodaetica et Cartographica Sinica,2001,40(1):22-27. (黄贤源, 翟国君, 隋立芬, 等.LS-SVM算法中优化训练样本对测深异常值剔除的影响[J].测绘学报, 2001,40(1):22-27.) |
| [5] | WANG Haidong, CHAI Hongzhou,WANG Min.Multibeam Bathymetry Fitting Based on Robust Kriging[J].Acta Geodaetica et Cartographica Sinica, 2011,40(2):238-248. (王海栋, 柴洪洲, 王敏.多波束测深数据的抗差Kriging拟合[J].测绘学报,2011,40(2):238-248.) |
| [6] | ZHANG Lihua,JIA Shuaidong,YUAN Jiansheng,et al. A Method for Controlling Shoal-bias Based on Uncertainty[J].Acta Geodaetica et Cartographica Sinica, 2012,41(2):184-190.(张立华, 贾帅东, 元建胜,等.一种基于不确定度的水深控浅方法[J].测绘学报, 2012,41(2):184-190.) |
| [7] | HUANG Motao, ZHAI Guojun, OUYANG Yongzhong,et al. Data Fusion Technique for Single Beam and Multibeam Echo Soundings[J].Acta Geodaetica et Cartographica Sinica, 2001,30(4):299-303. (黄谟涛, 翟国君, 欧阳永忠,等.多波束与单波束测深数据的融合处理技术[J].测绘学报,2001, 30(4):299-303.) |
| [8] | LI Jiabiao, WANG Xiaohua, HUA Zugen, et al. Multibeam Sounding Principles, Survey Technologies and Data Processing Methods[M]. Beijing: Ocean Press, 1999.(李家彪,王小华,华祖根, 等. 多波束勘测原理、技术和方法[M].北京:海洋出版社,1999.) |
| [9] | ZHAO Jianhu. Research on Multibeam Depth and Image Processing Methods[D]. Wuhan: Wuhan University,2002.(赵建虎. 多波束深度及图像数据处理方法研究[D]. 武汉:武汉大学,2002.) |
| [10] | AML OCEANOGRAPHIC.SV Plus V2. Sound Velocity Profiling Standard[EB/OL].[2012-10-05]. http://www.amloceanographic.com/core/media/media.nl/id.241/c.1068955/.f?h=1160b7b6a2b58dc8e2de. |
| [11] | L3 COMMUNICATIONS.SEA BEAM 2100 Multibeam Bathymetric Survey Mapping System,External Interface Specifications[EB/OL].[1999-08-15]. http://www.mbari.org/data/mbsystem/formatdoc/SB2100 External Interface.pdf. |
| [12] | KONGSBERG MARITIME AS.EM Series Multibeam Echo Sounders Datagram Formats, Revision[EB/OL].[2010-01-20]. http://www.ldeo.columbia.edu/res/pi/MB-System/formatdoc/EM_Datagram_Formats_RevP.pdf. |
| [13] | JONATHAN B,STEVE S, ARNOLD F.Streamlining Sound Speed Profile Pre-Processing: Case Studies and Field Trials[C]//Proceedings of US Hydrographic Conference. Florida:[s.n.],2011:25-28. |
| [14] | GENGX Y,ZIELINSKI A. Precise Multibeam Acoustic Bathymetry[J].Marine Geodesy,1999,22:157-167. |
| [15] | ZHAO Jianhu, LIU Jingnan.Development of Method in Precise Multibeam Acoustic Bathymetry[J].Geomatics and Information Science of Wuhan University, 2002,27(5):473-477. (赵建虎,刘经南.精密多波束测深系统位置修正方法研究[J]. 武汉大学学报:信息科学版, 2002,27(5):473-477.) |
| [16] | YANG Fanlin, LI Jiabiao, WU Ziyin, et al. A Post-Processing Method for the Removal of Refraction Artifacts in Multibeam Bathymetry Data[J]. Marine Geodesy,2007,30:235-247. |
| [17] | DING Jisheng, ZHOU Xinghua, TANG Qiuhua. Ray Tracking of Multibeam Echosounder System Based on Equivalent Sound Velocity Profile Method[J]. Hydrographic Surveying and Charting, 2004, 24(6):27-29.(丁继胜,周兴华,唐秋华.基于等效声速剖面法的多波束测深系统声线折射改正技术[J].海洋测绘,2004,24(6):27-29.) |
| [18] | KAMMERER E. A New Method for the Removal of Refraction Artifacts in Multibeam Echosounder Systems[D]. Saint John: University of New Brunswick, 2000. |
| [19] | DOUGLAS D H,PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J].Cartographica, 1973, 10(2): 112-122. |
| [20] | DINN D F, LONCAREVIC B D, COSTELLO G.The Effect of Sound Velocity Errors on Multi-beam Sonar Depth Accuracy[C]//Proceedings of ’95 IEEE Conference on Oceans.California:[s.n.],1995, 1001-1010. |
| [21] | CARIS. CARIS Multibeam Data Processing[EB/OL]. [2007-06-01]. http://www.caris.com. |