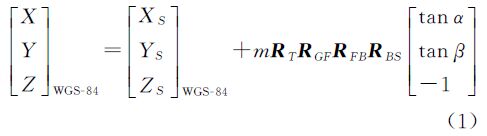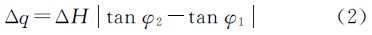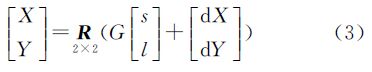2. 国家测绘地理信息局 卫星测绘应用中心,北京 101300
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation,Beijing 101300,China
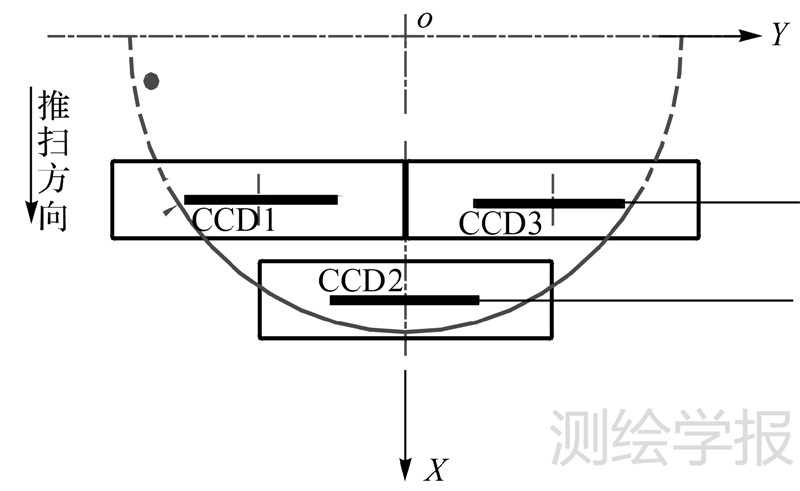
时间延时积分电荷耦合元件(TDI CCD)能在不降低成像空间分辨率的同时,有效地提高空间相机的成像灵敏度和信噪比,因而已逐渐取代常规CCD器件成为高分辨率光学推扫式相机的主流传感器[1]。目前,IKONOS、QuickBird、WorldView、Pleiades等高分辨率商业卫星以及我国资源一号02B (CBERS-02B)、资源一号02C星(ZY-1 02C)、资源三号(ZY-3)等卫星上的光学相机均采用TDI CCD器件作为成像传感器[2, 3, 4, 5, 6, 7, 8, 9, 10]。由于单片TDI CCD像元个数有限,在空间相机的设计上,为了保证获取较高空间分辨率和一定幅宽的影像,需要将多片TDI CCD 连接排列以获得较大的成像视场。然而受器件等物理因素的限制,多片TDI CCD很难直接在焦平面上按照共线方式进行物理排列,因而很多传感器采用了非共线的设计方式进行焦平面视场拼接,即将多片TDI CCD在焦平面上装配成上下交错的双列[11],例如,ZY-1 02C所搭载的高分辨率(HR)相机采用了典型的三片非共线设计,其焦平面排列方式如图 1所示。采用这种成像设计的TDI CCD相机获取的原始影像,受传感器焦平面摆放位置及其误差、相机光学系统畸变、偏流角控制偏差、卫星姿态变化、地面起伏、行积分时间变化等因素的影响,难以直接形成一幅覆盖相机全视场的连续无缝影像。为了满足后续影像产品的生产要求,必须对原始数据进行高精度内视场拼接,而多片TDI CCD的非共线设计使得分片影像间的错位和偏移特性较为显著和复杂,大大增加了高精度拼接处理的难度[12, 13, 14],因此针对该类相机成像数据进行内视场拼接的理论与方法研究,具有重要的理论意义和应用价值。
|
| 图 1 三片非共线TDI CCD焦平面排列示意图 Fig. 1 Focal plane assembly of three non-collinear TDI CCD chips |
出于对卫星设计参数以及卫星应用技术的保密,商业高分辨率卫星影像的前期视场拼接工作通常由数据供应方完成,可供参考的文献较少。目前,国内学者针对以CBERS-02B为代表的非共线TDI CCD成像数据的内视场拼接问题开展了一些研究工作。从理论基础上看,现有的方法可以分为像方拼接和物方拼接两大类。像方拼接本质上是基于像面变换的片间配准过程,如传统的基于片间平移的方法[14, 15]、基于分段仿射变换的方法[12, 16]和基于行积分时间归一化的方法[12]。像方拼接方法具有模型简单、计算量小的优点,通常能够保证拼接后的影像目视无缝,但缺点在于拼接后的影像失去了摄影测量的投影几何特性,无法对拼接影像进行高精度几何建模,这在较大程度上制约了影像的后续应用。相比而言,物方拼接具有严密的理论基础,其本质上是从相机的成像几何模型出发,利用相邻TDI CCD的物方摄影几何约束条件建立严格的相机内视场拼接模型,文献[17, 18]发展了基于虚拟线阵的方法[12],将其应用于ALOS/PRISM扫描仪、ZY-3全色多光谱相机等共线TDI CCD相机成像数据的内视场拼接处理中。文献[12, 19]提出了基于投影基准面的方法,并基于模拟的非共线TDI CCD数据对拼接模型的正确性进行了验证,但该方法采用了片间相对定向的策略,几何模型并不严谨。本文在此基础上,针对非共线TDI CCD成像数据的特点,提出了一种非共线TDI CCD成像数据内视场拼接方法。该方法直接建立在原始影像的传感器几何模型之上,并考虑了各种潜在的误差来源,对拼接处理的流程也进行了优化,无需进行片间相对定向处理,适合于业务化的运行系统。
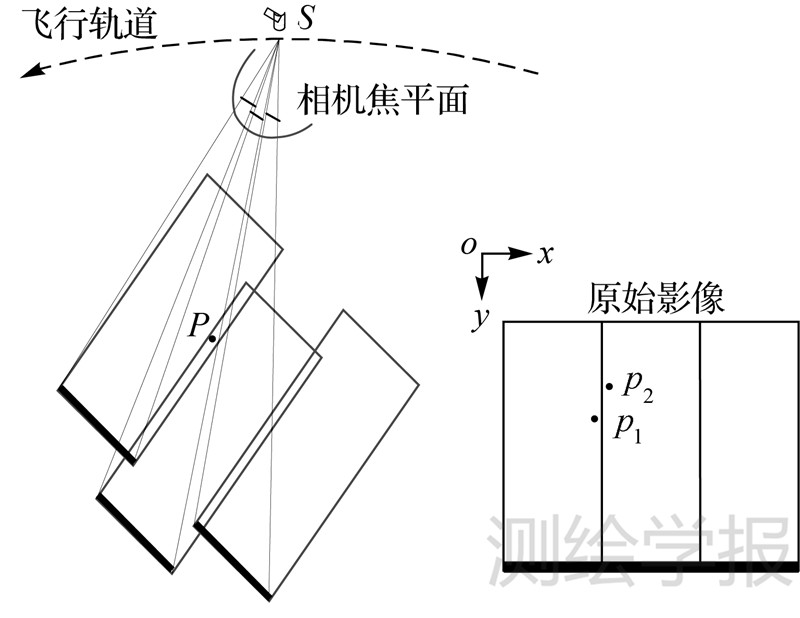
2 非共线TDI CCD的严格成像几何模型如图 2所示,以ZY-1 02C所搭载的HR相机为例,当相机沿轨推扫成像时,在焦平面上按非共线排列的三片TDI CCD共有一套轨道姿态、相机安装角、焦距和主点参数,基于传感器线阵与地面扫描投影线的映射关系,相机获得的地面覆盖范围由品字形分布的3条扫描带构成。根据HR相机焦平面设计特点[7],在垂轨方向相邻扫描带之间有大约30个像元的重叠,在沿轨方向上两侧扫描带相对于中间扫描带有大约2600行的成像时延。三片TDI CCD影像按成像时间或行计数对齐后即构成HR相机的原始影像。
|
| 图 2 HR相机成像模式和原始影像坐标系示意图 Fig. 2 Illustration of the imaging mode and the original image scene of HR camera |
在推扫成像时,每片TDI CCD都遵循线中心投影透视几何原理,所有分片TDI CCD影像的严格成像几何模型共同构成原始影像的传感器几何模型。每片TDI CCD影像的严格成像几何模型描述如下
式中,α、β分别为成像探元的光线相对于相机焦平面横轴和纵轴方向的指向角[20];m为摄影比例尺因子;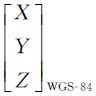 为地面点的WGS-84地心直角坐标;
为地面点的WGS-84地心直角坐标;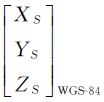 为成像时刻卫星在WGS-84地心直角坐标系下的坐标;RBS为是相机坐标系与卫星本体坐标系之间的旋转矩阵;RFB为卫星本体坐标系到轨道坐标系之间的姿态矩阵;RGF为轨道坐标系与地球惯性坐标系CIS之间的坐标转换矩阵;RT为像点成像时刻地球惯性坐标系CIS到地球固定坐标系CTS的坐标转换矩阵。
3 一种非共线TDI CCD成像数据内视场拼接方法
3.1 基本原理
为成像时刻卫星在WGS-84地心直角坐标系下的坐标;RBS为是相机坐标系与卫星本体坐标系之间的旋转矩阵;RFB为卫星本体坐标系到轨道坐标系之间的姿态矩阵;RGF为轨道坐标系与地球惯性坐标系CIS之间的坐标转换矩阵;RT为像点成像时刻地球惯性坐标系CIS到地球固定坐标系CTS的坐标转换矩阵。
3 一种非共线TDI CCD成像数据内视场拼接方法
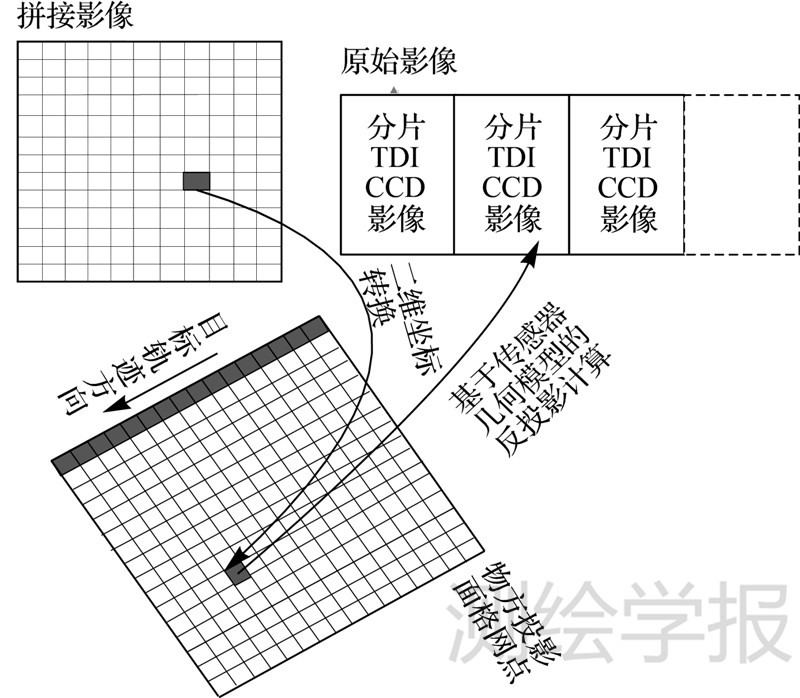
3.1 基本原理根据相机的严格成像几何模型,本文提出一种非共线TDI CCD成像数据内视场拼接方法。如图 3所示,假设物方投影面是定义在成像覆盖区域的平均高程面,沿卫星推扫成像的目标轨迹方向,对物方投影面上的成像覆盖区域划分等间隔格网,格网大小与原始影像的地面分辨率相一致。通过二维平移、旋转和缩放变换,将拼接影像像点与所定义的物方投影面格网点一一对应,然后基于原始影像的传感器几何模型,对物方投影面格网点进行反投影计算,得到其对应的原始影像像点坐标,由此便建立了从拼接影像像点到原始影像像点的坐标转换关系,进而采用间接法影像纠正的方式对原始影像进行重采样生成拼接影像。根据拼接影像像点在原始影像上的位置以及原始影像的传感器几何模型,得到拼接影像像点的等效摄影光线,由此构建拼接影像的等效摄影几何模型。该方法生成拼接影像的过程等效于沿卫星推扫成像的目标轨迹方向对原始影像进行了一次准系统几何校正。
|
| 图 3 拼接方法原理示意图 Fig. 3 Principle of the stitching method |
事实上,物方拼接就是利用拼接影像对地覆盖区域的连续性和原始影像的成像几何模型,建立拼接影像像点与原始影像像点的严格坐标映射关系。基于上述方法的原理,不难发现,良好的片间摄影几何约束条件是实现非共线TDI CCD成像数据严格无缝内视场拼接的几何基础,即要求片间几何定位精度具有一致性。如图 2所示,具体表现为,对于落在相邻两片TDI CCD成像地面覆盖重叠区内的任一物点P,基于原始影像的传感器几何模型分别反投影计算其在相邻两片影像上的像点,得到的一对像点p1和p2应满足共轭关系,即是一对同名像点。然而,在实际情况下,非共线TDI CCD在成像时存在的各类观测误差,均会不同程度地影响片间几何定位精度的一致性,应该在拼接处理之前对相机几何畸变及其安装角误差、卫星平台稳定性等参数进行检校,对各类系统误差进行补偿[7, 12]。
3.2 地物高差对拼接精度的影响除相机几何畸变及其安装角误差、卫星平台稳定性等参数外,物点与平均高程面之间的高差对非共线TDI CCD成像数据沿轨方向上的拼接精度也有一定影响[12]。如图 4所示,对于片间重叠区域内的任一物点P,假设其高程值与平均高程值的偏差为ΔH;φ1和φ2分别为相机两列TDI CCD偏场角的设计值;Δq表示由ΔH引起的影像拼接误差在物方的投影距离,则有
由式(2)可知,地物高差对物方拼接精度的影响程度与相邻两片TDI CCD的偏场角正切的差值成正比。对于HR相机,φ2≈1.15°,φ1≈0.7°,地面分辨率为2.36 m,根据式(2)计算,当地物点相对于平均高程面的高差达到300 m时,将引起2.36 m即1个像元的拼接误差。大多数情况下地物高差小于300 m,因此地物高差对拼接精度的影响均在一个像素以内,在保证精度的情况下将地物点的高程统一用平均高程替代,能降低地表模型的复杂度,提高物方拼接的效率。若相邻两片TDI CCD的偏场角非常相近乃至相等时,Δq取值接近于0,则在任何地形条件下的影响均可忽略不计。因此在非共线TDI CCD相机设计时,应尽量缩小两列TDI CCD沿轨方向的间距,以减弱地形起伏等因素对拼接精度的影响。

|
| 图 4 地物高差对拼接精度的影响 Fig. 4 Influence of the elevation error on stitching accuracy |
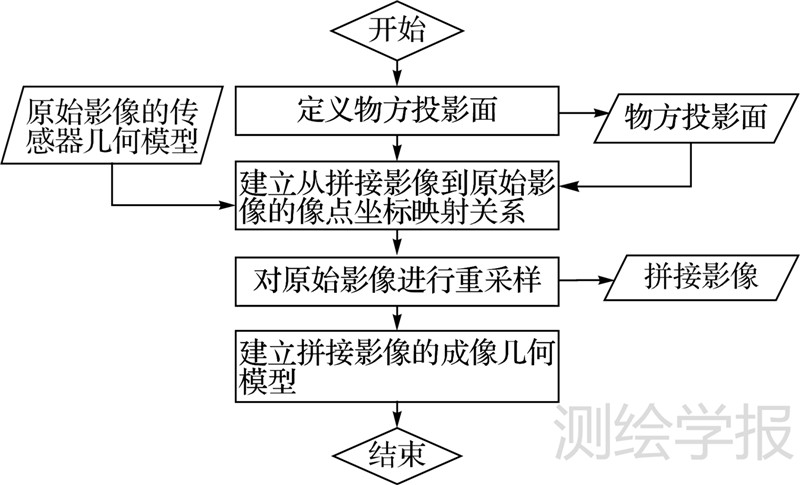
基于以上原理,本文非共线TDI CCD成像数据内视场拼接方法流程如图 5所示。
|
| 图 5 拼接方法流程图 Fig. 5 Workflow of the stitching method |
(1) 定义物方投影面。将物方投影面定义在成像区域所对应的通用横轴墨卡托(UTM)投影坐标系下,高程取WGS-84大地坐标系下的摄影区域平均椭球高H。
(2) 建立从拼接影像到原始影像的像点坐标映射关系。
① 基于原始影像的传感器几何模型、高程值H及UTM投影正算,分别计算原始影像第一列的首、尾像素在物方投影面上投影点坐标,将两个投影点的连线方向定义为推扫成像时的目标轨迹方向。
② 基于原始影像的传感器几何模型、高程值H及UTM投影正算,确定原始影像在物方投影面上的投影覆盖区域AOP(area of projection)。
③ 确定拼接影像在物方投影面上的投影覆盖区域AOI(area of interest),沿推扫成像时的目标轨迹方向,确定AOP的最小外廓矩形AOI,即拼接影像在物方投影面上的投影覆盖区域。
④ 根据原始影像的地面分辨率确定物方投影面采样间隔,对AOI划分等间隔格网,将拼接影像的像点与格网点一一对应,沿目标轨迹和垂直于目标轨迹方向的格网数目分别对应拼接影像的行数和列数。拼接影像与物方投影面之间的坐标转换关系如式(3)所示
式中,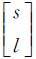 为拼接影像像点的像素坐标;
为拼接影像像点的像素坐标;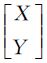 为拼接影像像点在物方投影面的投影点坐标;G为物方投影面采样间隔大小;
为拼接影像像点在物方投影面的投影点坐标;G为物方投影面采样间隔大小;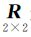 是根据目标轨迹方向确定的二维坐标旋转矩阵;
是根据目标轨迹方向确定的二维坐标旋转矩阵;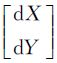 为坐标平移量。
为坐标平移量。
⑤ 基于UTM投影反算得到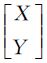 对应的经纬度坐标
对应的经纬度坐标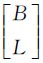 ,然后基于原始影像的传感器几何模型,由物方投影面投影点的大地坐标
,然后基于原始影像的传感器几何模型,由物方投影面投影点的大地坐标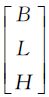 计算对应的原始影像像点坐标
计算对应的原始影像像点坐标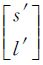 。
。
由此即建立了从拼接影像到原始影像的像点坐标映射关系。
(3) 对原始影像进行重采样,生成拼接影像。根据拼接影像到原始影像的像点坐标映射关系,采用间接法影像纠正的方式对原始影像进行重采样,生成拼接影像。对于高差较大区域,可在片间重叠区进一步提取若干连接点,并在一定范围进行影像局部纠正[16],以达到子像素级的目视拼接精度。
(4) 构建拼接影像的成像几何模型。
① 对于拼接影像上的任一像点,令其像素坐标为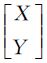 ,根据建立的拼接影像到原始影像的像点坐标映射关系,计算对应的原始影像像点坐标
,根据建立的拼接影像到原始影像的像点坐标映射关系,计算对应的原始影像像点坐标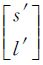 。
。
② 通过原始影像上的影像坐标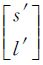 加上高程h,利用原始影像的传感器几何模型,计算对应的地面点大地坐标
加上高程h,利用原始影像的传感器几何模型,计算对应的地面点大地坐标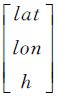 。
。
③ 根据步骤①和步骤②得到拼接影像等效摄影几何模型的正算公式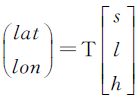 ,这里,T表示由拼接影像像点坐标正算到大地经纬度坐标的转换关系。根据该正算公式构建像方均匀分布的控制点立体格网,利用与地形无关的RPC求解方式[15]得到拼接影像的有理函数模型(RFM)参数。
,这里,T表示由拼接影像像点坐标正算到大地经纬度坐标的转换关系。根据该正算公式构建像方均匀分布的控制点立体格网,利用与地形无关的RPC求解方式[15]得到拼接影像的有理函数模型(RFM)参数。
为验证本文方法的效果和可行性,本文采用ZY-1 02C卫星HR相机成像数据对方法进行试验验证。ZY-1 02C卫星上所搭载的HR相机每片TDI CCD 有4096像元,在沿轨方向上CCD1、CCD3与CCD2有大约2600行的成像时延,在垂轨方向上有大约30像素左右的重叠,相机地面分辨率为2.36 m,幅宽27 km。本文给出了该相机获取的不同地形条件下的两景数据的试验情况(图 6、图 7),表 1列出了试验数据的相关信息。

|
| 图 6 数据1试验结果 Fig. 6 Experimental results of data 1 |
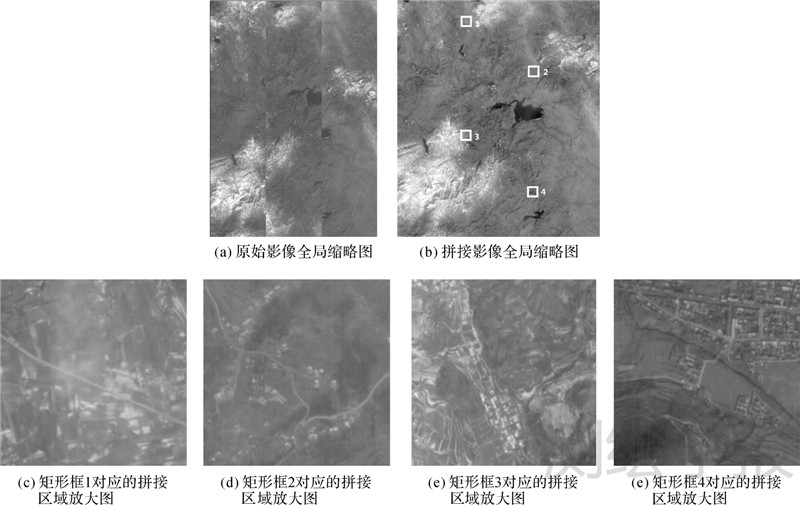
|
| 图 7 数据2试验结果 Fig. 7 Experimental results of data 2 |
| 影像覆盖区域 | 获取时间 | 传感器 | 原始影像大小 | 地形条件 | 参考数据源 | |
| 数据1 | 北京 | 2012-02-01 | ZY-1 02C/HR | 17 575行×12 288 列 | (平原、丘陵)平均高程约20 m最大高程约30 m | 2.5 m分辨率卫星正射影像;30 m采样间隔DEM |
| 数据2 | 河南登封 | 2012-01-23 | ZY-1 02C/HR | 17 575行×12 288列 | (山地、高山地)平均高程约340 m最大高程约1450 m | 1 m分辨率航空正射影像;5 m采样间隔DEM |
本文分别采用目视(定性)评价以及统计分析拼接影像的RFM拟合精度及其像点定位中误差(定量),对视场拼接的效果以及精度进行评价。
4.1 视场拼接及目视评价对表 1中的两景数据分别进行拼接试验,检查所生成的拼接影像是否满足目视无缝的要求,即在拼接区域是否存在错位现象。
数据1(图 6)所对应的北京地区地势较为平坦,地物高差所引起的拼接误差很小,远在1个像素以内;数据2(图 7)所对应的河南登封地区属于山地和高山地地形,地物相对于平均高程的高差最大达到了1100 m以上,根据地物高差对拼接精度的影响可知,由此会引起最大3.67个像素的局部拼接误差。为了克服该影响,在片间重叠区提取了若干连接点,并在拼接区域进行局部像面纠正[16]从而实现子像素级的目视拼接精度。数据1和数据2拼接前后的影像分别如图 6(b)和图 7(b)所示,由拼接区域的放大图可以看出,拼接影像达到了目视无缝的精度要求。
4.2 拼接影像RFM拟合精度评价按照本文3.3节步骤4的描述构建上述两景拼接影像的RFM,评价RFM对等效摄影几何模型的拟合精度。采用 256像素×256像素的像面格网,高程分层为5,这些格网点全部作为控制点;再平移半个格网距离、格网大小不变,再计算出另一批虚拟格网点作为检查点。控制点用于求解分母不相等的三阶RFM 模型参数[20],检查点用于统计RFM拟合精度。如表 2 所示,对两景拼接影像构建RFM的拟合精度均在0.000 3个像素以内,完全可满足影像生产应用的需求。
| 像素 | |||||
| 行方向 | 列方向 | ||||
| 最大误差 | 中误差 | 最大误差 | 中误差 | ||
| 数据1 | 0.000 281 | 0.000 135 | 0.000 253 | 0.000 114 | |
| 数据2 | 0.000 277 | 0.000 136 | 0.000 241 | 0.000 112 | |
br> 本文采用统计像点定位中误差的方式对拼接影像的几何精度进行分析评价。其过程如下:
(1) 利用提供的参考数据,在拼接影像范围内提取均匀分布的控制点。对于数据1,在拼接影像范围选取了268个控制点;对于数据2,在拼接影像范围内选取了205个控制点。
(2) 基于拼接影像的RFM和控制点的地面经纬度坐标反投影计算其像点坐标,与其量测的像点坐标进行比较求差,得到无控制点情况下像点定位误差。如表 3所示,经统计,数据1行和列两个方向上的像点定位中误差分别为1.92个像素和2.46个像素,数据2行和列两个方向上的像点定位中误差分别为1.57个像素和2.47个像素。
| 像素 | |||||||||
| 方法 | 影像 | 无控制点 | 有控制点(像方仿射变换模型) | 有控制点(像方多项式变换模型) | |||||
| 行方向中误差 | 列方向中误差 | 行方向中误差 | 列方向中误差 | 行方向中误差 | 列方向中误差 | ||||
| 本文的方法 | 数据1 | 1.92 | 2.46 | 2.37 | 1.69 | — | — | ||
| 数据2 | 1.57 | 2.47 | 1.42 | 2.44 | — | — | |||
| 基于行积分时间归一化的方法 | 数据1 | 8.32 | 18.55 | 4.04 | 5.68 | 1.45 | 3.12 | ||
| 数据2 | 20.70 | 10.39 | 2.56 | 6.21 | 3.18 | 2.11 | |||
| 基于分段仿射变换的方法 | 数据1 | 3.15 | 11.18 | 1.55 | 3.48 | 1.05 | 2.85 | ||
| 数据2 | 6.72 | 14.76 | 2.27 | 6.43 | 1.31 | 3.02 | |||
(3) 利用控制点数据求解拼接影像RFM的像方仿射变换补偿参数[21],进而统计有控制点情况下像点定位误差。如表 3所示,经统计,数据1行和列两个方向上的像点定位中误差分别为2.37个像素和1.69个像素,数据2行和列两个方向上的像点定位中误差分别为1.42个像素和2.44个像素。
根据方法的原理,拼接影像无控制点几何精度与拼接过程中所采用的原始影像严格成像几何模型的精度是一致的,通过引入几何检校对模型误差进行补偿,在实现子像素级目视无缝拼接精度的同时,还可以消除拼接影像中的几何畸变。因此基于该方法生成的拼接影像,用户可以无须控制点或只选取极少量控制点就能获得具有较高几何质量的拼接影像,满足后续应用的需求。试验也表明,对于数据1和数据2,拼接影像无控制点情况下的像点定位中误差在2.5个像素以内,即使利用控制点对拼接影像的RFM误差进行补偿之后,反映拼接影像内部畸变的中误差指标值也没有明显变化,这说明通过在原始影像的传感器几何模型中引入相机几何检校结果已经较好地去除了系统性的几何畸变,因此在有控制点情况下,控制点对内部畸变的改善效果不明显。
4.4 与像方拼接方法的比较
本文还将基于行积分时间归一化的方法[12]以及基于分段仿射变换的方法[12, 16]等两种像方方法与本文方法进行了对比。这两种像方拼接方法对数据1和数据2所生成的拼接影像均能满足目视无缝的要求。但由于像方拼接后影像实际上失去了摄影测量的投影几何特性,因此只能对其构建了一种近似等效摄影几何模型[12],本文在此基础上进行了精度统计,统计的像点定位中误差见表 3。从表 3可以看出,无控制点情况下,基于行积分时间归一化的方法像点定位中误差最大接近21个像素,基于分段仿射变换的方法像点定位中误差最大也接近12个像素,表明影像内部几何精度较低。而利用控制点采用像方仿射变换模型补偿RFM系统误差之后,像点定位中误差有所改善,基于行积分时间归一化的方法最大仍接近7个像素,基于分段仿射变换的方法中误差则与本文方法接近。采用像方多项式变换模型补偿RFM系统误差之后,像点定位中误差均进一步减小,与本文方法接近。但由于选取的控制点较多,在实际应用中工作量太大,因此本文方法更具优越性。
5 结 论本文从相机的严格成像几何模型出发,提出了一种非共线TDI CCD成像数据内视场拼接方法。该方法根据拼接影像像点在原始影像上的位置以及原始影像的传感器几何模型,得到拼接影像像点的等效摄影光线,由此构建拼接影像的等效摄影几何模型。为了验证方法的效果及可行性,本文用国产ZY-1 02C卫星高分辨率相机的成像数据进行了试验验证。试验结果及定性、定量评价表明,本文方法切实可行,拼接影像的生成过程等效于沿卫星推扫成像的目标轨迹方向对原始影像进行了一次准系统几何校正,能满足影像后续处理和应用的需求。目前,该方法已成功应用于国产资源卫星地面处理系统。本文方法不仅适用于ZY-1 02C卫星高分辨率相机的成像数据的视场拼接处理,也同样适用于其他非共线设计的TDI CCD相机高分辨率成像数据的视场拼接处理。如果具有高精度的相机几何定标数据,可进一步提高本文方法拼接处理的几何精度。
| [1] | HUANG Qiaolin, JIANG Wei. A Study of the New Direction of Space-borne Hi-resolution Optical Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 48-50. (黄巧林,姜伟. 高分辨率航天光学遥感器发展新思路研究[J]. 航天返回与遥感,2007,28(4):48-50.) |
| [2] | YANG Bingxin. Characteristics and Main Specifications of IKONOS and QuickBird2 Satellite Camera: Some Points for Developing such Like Satellite Camera[J]. Spacecraft Recovery & Remote Sensing, 2002, 23(4): 14-16. (杨秉新. 美国IKONOS 和QuickBird-2 卫星相机的主要性能和特点分析及看法[J]. 航天返回与遥感,2002,23(4):14-16.) |
| [3] | UPDIKE T, COMP C. Radiometric Use of WorldView-2 Imagery: Technical Note[DB/OL]. Colorado: [s.n.], 2010-11-01. http://www.digitalglobe.com/sites/default/files/. |
| [4] | JACOBSEN K. Calibration of Optical Satellite Sensors[C]// Proceedings of International Calibration and Orientation Workshop EuroCOW. Casteldefels: [s.n.], 2006. |
| [5] | MATERNE A, BARDOUX A, GEOFFRAY H, et al. Backthinned TDI CCD Image Sensor Design and Performance for the Pleiades High Resolution Earth Observation Satellites[C]// Proceedings of Sixth International Conference on Space Optics. Noordwijk: European Space Agency, 2006. |
| [6] | ZHOU Shengli. Analysis of Three-linear TDI CCD Array Application in Cartography Satellite[J]. Spacecraft Engineering, 2007, 16(4): 19-22. (周胜利. 三线阵TDI CCD在测图卫星中的应用分析[J]. 航天器工程, 2007, 16(4): 19-22.) |
| [7] | YANG Bo, WANG Mi. On-orbit Geometric Calibration Method of ZY-1 02C Panchromatic Camera[J]. Journal of Remote Sensing, 2013, 17(5): 1175-1190. (杨博,王密. 资源一号02C 卫星全色相机在轨几何定标方法[J]. 遥感学报, 2013, 17(5): 1175-1190.) |
| [8] | LI Deren. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322. (李德仁. 我国第一颗民用三线阵立体测图卫星: 资源三号卫星[J]. 测绘学报, 2012, 41(3): 317-322.) |
| [9] | JIANG Yonghua, ZHANG Guo, TANG Xingming, et al. High Accuracy Geometric Calibration of ZY-3 Three Line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529. (蒋永华, 张过, 唐新明, 等.资源三号测绘卫星三线阵影像高精度几何检校[J].测绘学报, 2013,42(4):523-529.) |
| [10] | TANG X M, ZHANG G, ZHU X Y, et al. Triple Linear-array Image Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. International Journal of Image and Data Fusion(IJIDF), 2013, 4(1): 33-51. |
| [11] | YANG Hua, GUO Yue, FU Ruimin. Study on Field Butting of TDI CCD[J]. Optical Technique, 2003, 29(2): 226-228. (杨桦,郭悦,伏瑞敏. TDI CCD的内视场拼接[J]. 光学技术,2003,29(2):226-228.) |
| [12] | HU Fen. Research on Inner FoV Stitching Theories and Algorithms for Sub-images of Three Non-collinear TDI CCD Chips[D]. Wuhan: Wuhan University, 2010. (胡芬. 三片非共线TDI CCD成像数据内视场拼接理论与算法研究[D]. 武汉: 武汉大学, 2010.) |
| [13] | LONG Xiaoxiang, WANG Xiaoyan, ZHONG Huimin. Analysis of Image Quality and Processing Method of a Space-borne Focal Plane View Splicing TDI CCD Camera[J]. Scientia Sinica: Informationis, 2011, 41(sup): 19-31. (龙小祥,王小燕,钟慧敏. 星载焦面视场拼接TDI CCD相机成像质量及处理方法分析[J]. 中国科学: 信息科学, 2011, 41(增刊): 19-31.) |
| [14] | LI Shiwei, LIU Tuanjie, WANG Hongqi. Image Mosaic for TDI CCD Push-broom Camera Image Based on Image Matching[J]. Remote Sensing Technology and Application, 2009, 24(3): 374-378. (李世威, 刘团结, 王宏琦. 基于图像匹配的CBERS-02B卫星HR相机图像拼接方法[J]. 遥感技术与应用, 2009, 24(3): 374-378.) |
| [15] | LU Jinbo. Automatic Mosaic Method of Large Field View and Multi-channel Remote Sensing Images of TDI CCD Cameras[D]. Jilin: Changchun Institute of Optics, Fine Mechanics and Physics of CAS, 2010. (禄金波. TDI CCD大视场多通道图像自动拼接方法[D]. 吉林:中国科学院长春光学精密机械与物理研究所,2010.) |
| [16] | HU Fen, WANG Mi, JIN Shuying. Satellite-borne Three-non-colinear TDI CCD(time delayed and integration charge coupled device) Image Splicing Method Based on Segmented Affine Transformation:CN 101799293 B[P]. 2011-11-02. (胡芬,王密,金淑英. 基于分段仿射变换的星载三片非共线TDI CCD影像拼接方法: 中国, 101799293 B[P]. 2011-11-02.) |
| [17] | ZHANG Guo, LIU Bin, JIANG Wanshou. Inner FoV Stitching Algorithm of Spaceborne Optical Sensor Based on the Virtual CCD Line[J]. Journal of Image and Graphics, 2012, 17(6): 696-701. (张过,刘斌,江万寿. 虚拟CCD线阵星载光学传感器内视场拼接[J]. 中国图象图形学报,2012,17(6):696-701.) |
| [18] | PAN Hongbo, ZHANG Guo, TANG Xinming, et al. The Geometrical Model of Sensor Corrected Products for ZY-3 Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 516-522. (潘红播,张过,唐新明,等. 资源三号测绘卫星传感器校正产品几何模型[J]. 测绘学报, 2013, 42(4): 516-522.) |
| [19] | HU F, WANG M, JIN S Y. An Algorithm for Mosaicking Non-collinear TDI CCD Chip Images Based on Reference Plane in Object-space[C]// Proceedings of the 6th International Symposium on Digital Earth(ISDE6). Beijing: SPIE, 2009. |
| [20] | ZHANG Guo. Rectification for High Resolution Remote Sensing Image under Lack of Ground Control Points[D]. Wuhan: Wuhan University, 2005. (张过. 缺少控制点的高分辨率卫星遥感影像几何纠正[D]. 武汉:武汉大学,2005.) |
| [21] | TAO C V, HU Y.A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001,67(12):1347-1357. |