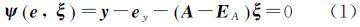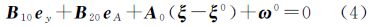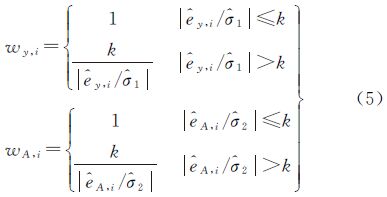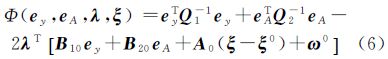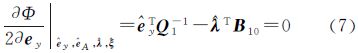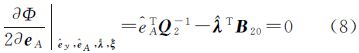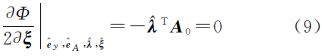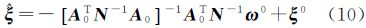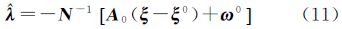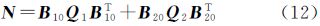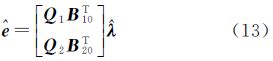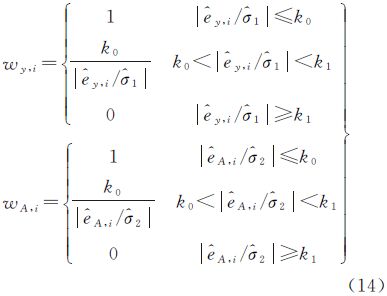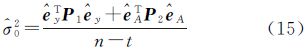2. 东华理工大学 江西省数字国土重点实验室,江西 南昌 330013;
3. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉 430079
2. Jiangxi Province Key Lab for Digital Land,East China Institute of Technology,Nanchang 330013,China;
3. Key Laboratory of Precise Engineering and Industry Surveying of National Administration of Surveying,Mapping and Geoinformation,Wuhan 430079,China
1 引 言
在测绘地理信息领域,无论是线性模型还是非线性模型,如建筑物表面模型拟合、坐标转换、GPS高程拟合等,都需要对模型的未知参数进行估计。最小二乘(least squares,LS)估计理论由Gauss和Legendre在18世纪末19世纪初提出。由于它是最优线性无偏估计,且简单方便,已广泛应用于参数估计中。然而,LS平差理论认为函数模型中系数矩阵没有误差或不考虑系数矩阵的误差,所有的误差都限于观测向量。由于受采样误差、模型误差、仪器误差、人为误差等多方面的影响,系数矩阵也可能含有误差,例如坐标转换中的原坐标也是含有误差的观测量,此时采用LS方法进行参数估计得到的结果从统计观点看就是有偏的[1]。
总体最小二乘(total least squares,TLS)估计方法能够同时考虑观测向量和系数矩阵的误差[2, 3, 4, 5],引起了测绘地理信息学者的大量研究[6, 7, 8, 9, 10, 11, 12, 13, 14]。近年来,由总体最小二乘扩展的加权总体最小二乘也引起了相关研究[15, 16, 17, 18, 19]。然而,这些加权总体最小二乘方法均没有考虑观测数据中存在粗差的情况,而现代测量手段趋向于向数据采集的自动化和快速化发展,其观测量中同时包含了粗差、系统误差和随机误差。在平差处理中,如何发现和区分粗差观测量,并消除其影响,是提高平差成果精度的一个关键问题。稳健估计(robust estimation) 正是针对这一缺陷而提出来的[20],其目的在于构造某种估计方法,使其对于模型误差、特别是粗差具有较强的抵抗能力。
文献[21]在非线性观测方程中对随机误差和未知参数进行线性化,应用LS,通过交替迭代,得到非线性高斯-赫尔默特模型下由LS平差获得的TLS解[22]。针对文献[21]没有考虑观测数据中可能存在粗差的情况,文献[22, 23]提出基于Huber权函数的稳健总体最小二乘方法,由于它们均考虑了权矩阵,其实质应分别为加权总体最小二乘(weighted total least squares,WTLS)方法和基于Huber权函数的稳健加权总体最小二乘(robust weighted total least squares based on Huber weight function,RWTLS-Huber)方法。关于权函数的选取,在测量实践中认为IGG(institute of geodesy and geophysics,由周江文教授提出)权函数更优。本文通过公式推导,给出基于IGG权函数的稳健加权总体最小二乘(robust weighted total least squares based on IGG weight function,RWTLS-IGG)方法的具体求解步骤,并选取合理的评定指标,通过模拟数据和真实数据试验,系统地评估了这种方法,并将结果与WTLS方法、RWTLS-Huber方法进行比较分析。
2 现有稳健加权总体最小二乘方法同时考虑观测向量和系数矩阵误差的EIV(errors-in-variables)模型为
式中,y为n×1观测向量;ey为观测向量y所对应的随机误差向量;A为n×t系数矩阵;EA为系数矩阵A所对应的随机误差矩阵;ξ为t×1未知参数向量; 为随机误差向量,其中eA=vec(EA)指的是将矩阵EA向量化变换为eA(即拉直运算)。
为随机误差向量,其中eA=vec(EA)指的是将矩阵EA向量化变换为eA(即拉直运算)。
EIV模型本质上是一种非线性模型,因此也可以将其当作非线性高斯-赫尔默特模型进行线性化。令随机误差向量和未知参数向量的近似值分别为e0和ξ0,则式(1)可线性化为[21, 22, 23]
式中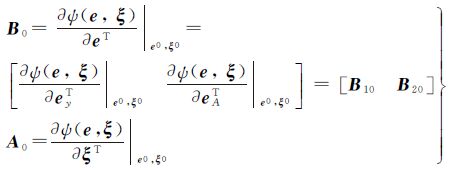
联合式(2)和式(3)可得观测方程
将Huber权函数用于WTLS方法中[22, 23],采用选权迭代法进行求解,形成RWTLS-Huber方法,其权因子为
式中,wy,i、wA,i分别为观测向量和系数矩阵第i点的权因子; y,i、
y,i、 A,i分别为观测向量和系数矩阵第i点的残差;
A,i分别为观测向量和系数矩阵第i点的残差; 1、
1、 2分别为观测向量和系数矩阵的中误差;k为常数(一般取k=2)。
2分别为观测向量和系数矩阵的中误差;k为常数(一般取k=2)。
由式(5)可分别求得观测向量y和系数矩阵A的权因子矩阵
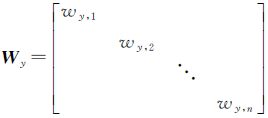
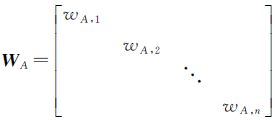
利用拉格朗日乘数λ构造目标函数
对其求偏导数 经过整理可得 式中 相应的残差向量为 将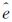 、
、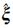 作为新的初值,重新定权后代入式(10)计算,通过迭代,直到参数向量满足收敛条件。
作为新的初值,重新定权后代入式(10)计算,通过迭代,直到参数向量满足收敛条件。
文献[22, 23]通过模拟的三维相似坐标转换进行试验,证明了该方法的有效性。然而,在基于选权迭代法的稳健估计方法中,Huber权函数并不是最优的,因此有必要采用效果更好的权函数进行稳健估计。
3 一种基于IGG权函数的稳健加权总体最小二乘方法在LS的稳健估计中,对等价权函数的选取方法主要有Huber权函数、丹麦权函数和IGG权函数等[24]。已有文献及大量实际计算表明,IGG权函数更适于测量计算[25, 26],其中IGG权因子为
式中,k0、k1为常数(一般取k0=1.5,k1=2.5)。根据以上推导公式,得出RWTLS-IGG方法的解算步骤:
(1) 取LS解为初始值ζ0。
(2) 根据式(13)计算残差向量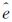 i(设初始值为零向量),同时分别求得观测向量y和系数矩阵A的中误差
i(设初始值为零向量),同时分别求得观测向量y和系数矩阵A的中误差 1、
1、 2。
2。
(3) 由实际观测条件确定观测向量y和系数矩阵A的初始权矩阵Py和PA,根据式(14)分别确定观测向量y和系数矩阵A的权因子矩阵Wy、WA(设初始值为单位矩阵),从而得到观测向量y和系数矩阵A的权矩阵P1和P2,对应的协因数阵为Q1和Q2。
(4) 利用式(10)计算参数向量ζi+1。
(5) 重复(2)-(4)步,直到||ζi+1-ζi||<ε,迭代结束。
4 试验设计以上简要阐述了RWTLS-IGG方法,为了验证这种方法的有效性,下面采用模拟数据和真实数据进行试验,将所得结果与WTLS方法和RWTLS-Huber方法进行比较分析。
4.1 评定指标在模拟试验中,通过单位权方差和均方误差来定量地评估WTLS方法、RWTLS-Huber方法和RWTLS-IGG方法参数估计结果的好坏。其中,单位权方差为
式(15)所得单位权方差是有偏的,因偏差较小,故对结果几乎没有影响[15, 22]。
虽然比较单位权方差能直接分析估计方法之间的差异,但它只反映了估计方法本身的性能。因此,在模拟试验中,笔者使用均方误差作为另一个指标来评定参数估计结果的准确度,其中均方误差越小,估计结果的准确度越高。根据所得参数向量估计值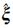 ,求出均方误差
,求出均方误差
设计模型Y=2X1+3X2,每次试验均模拟100组观测数据,其中X1、X2为1~10之间的随机整数,相应的Y为5~50之间的随机整数。然后在模拟的观测数据中添加服从正态分布N(0,σ2I)(σ=0.1,I为单位阵)的随机误差,使得观测向量和系数矩阵都有误差(见图 1),假设模拟数据为等权观测。为了进一步比较3种方法的抗差能力,根据粗差在观测数据中存在的概率一般不超过10%[27]的原则,同时考虑粗差大小对参数估计结果的影响,采用两种方式进行模拟试验:①控制粗差的大小为8σ,改变每个观测量中粗差的数量;②控制每个观测量中粗差的数量为5(即粗差在数据中存在的概率为5%),改变粗差的大小。
|
| 图 1 加入随机误差后的模拟数据 Fig. 1 Simulation data for adding random errors |
在对模拟数据进行试验的基础上,结合真实数据,将稳健WTLS方法应用到真实数据的参数估计中。以文献[17]中数据作为样本(见表 1),设直线方程为y=ξ1+ξ2x。
| 点号 | x | P1 | y | P2 |
| 1 | 0.0 | 1 000.0 | 5.9 | 1.0 |
| 2 | 0.9 | 1 000.0 | 5.4 | 1.8 |
| 3 | 1.8 | 500.0 | 4.4 | 4.0 |
| 4 | 2.6 | 800.0 | 4.6 | 8.0 |
| 5 | 3.3 | 200.0 | 3.5 | 20.0 |
| 6 | 4.4 | 80.0 | 3.7 | 20.0 |
| 7 | 5.2 | 60.0 | 2.8 | 70.0 |
| 8 | 6.1 | 20.0 | 2.8 | 70.0 |
| 9 | 6.5 | 1.8 | 2.4 | 100.0 |
| 10 | 7.4 | 1.0 | 1.5 | 500.0 |
以上采用模拟数据和真实数据进行试验,分别利用WTLS方法和两种稳健WTLS方法进行参数估计,下面从各种方法的模型、单位权方差和均方误差等方面对他们的估计结果进行比较分析。
5.1 模拟试验结果与分析首先通过模拟试验探讨本文提出方法的有效性,根据含随机误差和粗差的模拟数据进行试验。采用本文提出的RWTLS-IGG方法对模型进行参数估计,并将其与WTLS方法和RWTLS-Huber方法进行比较。
5.1.1 模拟试验1的结果与分析:粗差数量的影响图 2表示每个观测量中的粗差数量为0到10时3种方法所得的单位权方差。从图中可以看出,当观测数据中不含粗差时,WTLS方法的单位权方差在0.010左右,但当数据中的粗差数量不断增多时,WTLS方法的单位权方差也呈现不断增大的趋势,最大值甚至超过0.070,其结果远大于仅含随机误差时的单位权方差,这说明WTLS方法的单位权方差明显受粗差数量的影响。RWTLS-Huber方法所得单位权方差虽然小于WTLS方法,但其同样随粗差数量的增多而呈现明显增大的趋势,这说明RWTLS-Huber方法抗差效果不好。而RWTLS-IGG方法的单位权方差却很小,且随粗差数量增多的影响较小,可认为其抗差效果更优。

|
| 图 2 模拟试验中粗差数量变化时的单位权方差 Fig. 2 Variance of unit weight as an increase in the numbers of gross errors in simulation data experiment |
除了对单位权方差的比较,更需要注意均方误差的结果。图 3表示粗差数量不同时均方误差的变化,从中可以明显地看出:①当观测数据中不含粗差时,3种方法所得的均方误差相近,但当粗差数量增多时,两种稳健WTLS方法所得的均方误差明显小于WTLS方法,这表明两种稳健WTLS方法对粗差有一定的抵抗能力;②WTLS方法所得均方误差随着粗差数量的增多而呈现增大的趋势,这说明采用WTLS方法进行参数估计时,不同数量的粗差对结果的影响也不同;③RWTLS-Huber方法同样受粗差数量变化的影响,且其均方误差较大,说明其参数估计结果不好;④RWTLS-IGG方法所得均方误差小于RWTLS-Huber方法,这说明RWTLS-IGG方法的参数估计结果更可靠。
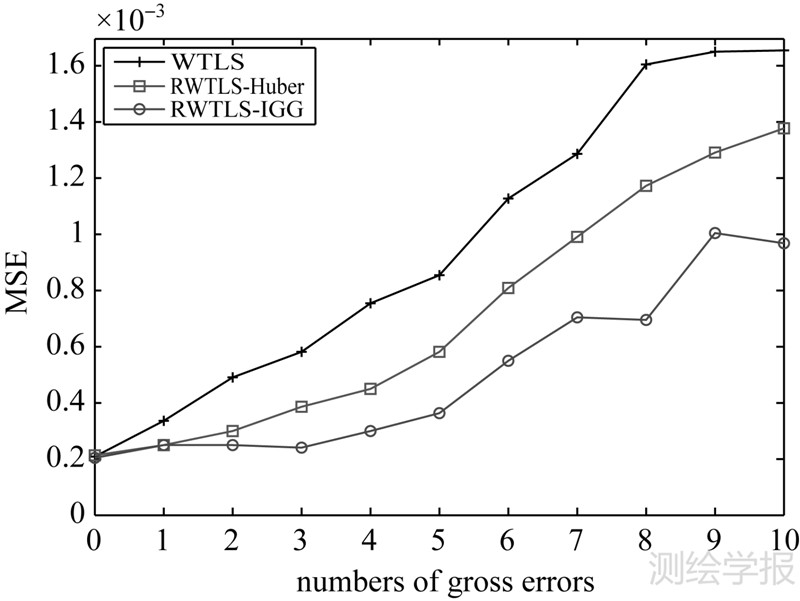
|
图 3 模拟试验中粗差数量变化时的均方误差
Fig. 3 Mean square error of estimated parameter vectors 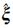 as an increase in the numbers of gross errors in simulation data experiment as an increase in the numbers of gross errors in simulation data experiment
|
在评估粗差大小对参数估计结果的影响时,首先比较单位权方差的结果。图 4表示粗差大小从0.3~1.3时,WTLS方法和两种稳健WTLS方法所得的单位权方差。结果表明WTLS方法所得单位权方差均在0.012以上,并随着粗差大小的增加而增大,最大值甚至超过0.081,其结果远大于不含粗差时的单位权方差0.010,说明WTLS方法的单位权方差明显受粗差大小的直接影响。显然RWTLS-Huber方法所得单位权方差小于WTLS方法,但同样受粗差大小变化的影响较大,这是因为Huber权函数缺少淘汰段,不利于提高估值的抗差能力,从而造成RWTLS-Huber方法的单位权方差结果不好。而RWTLS-IGG方法所得单位权方差很小,且随粗差大小变化的影响较小,这说明RWTLS-IGG方法抵抗粗差的效果更好。
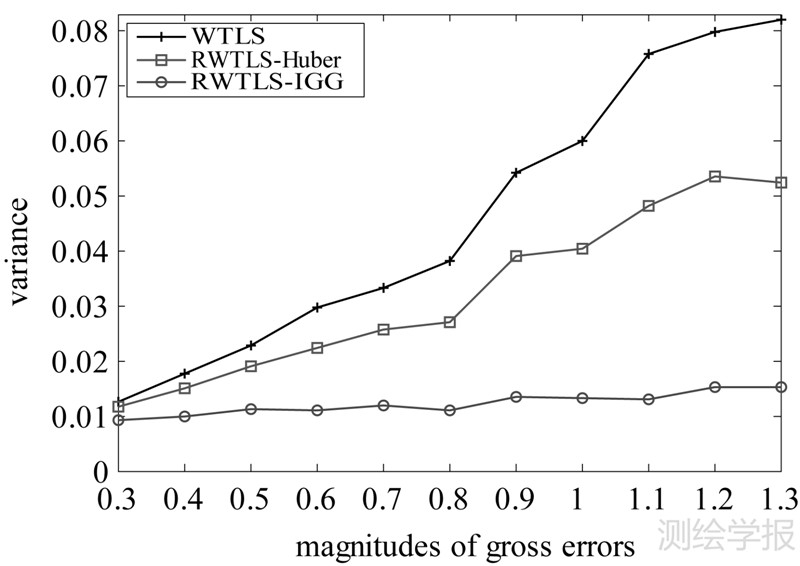
|
| 图 4 模拟试验中粗差大小变化时的单位权方差 Fig. 4 Variance of unit weight as an increase in the magnitudes of gross errors in simulation data experiment |
从图 5中可以明显地看出,3种方法所得均方误差均随着粗差大小的增加而呈现增大的趋势,其中两种稳健WTLS方法所得的均方误差明显小于WTLS方法,这说明两种稳健WTLS方法能够一定程度上抵抗数据中的粗差。RWTLS-Huber方法的均方误差大概在0.235×10-3至1.100×10-3之间,而RWTLS-IGG方法所得均方误差却在0.270×10-3至0.468×10-3之间,因此RWTLS-IGG方法的均方误差明显比RWTLS-Huber方法更稳健。
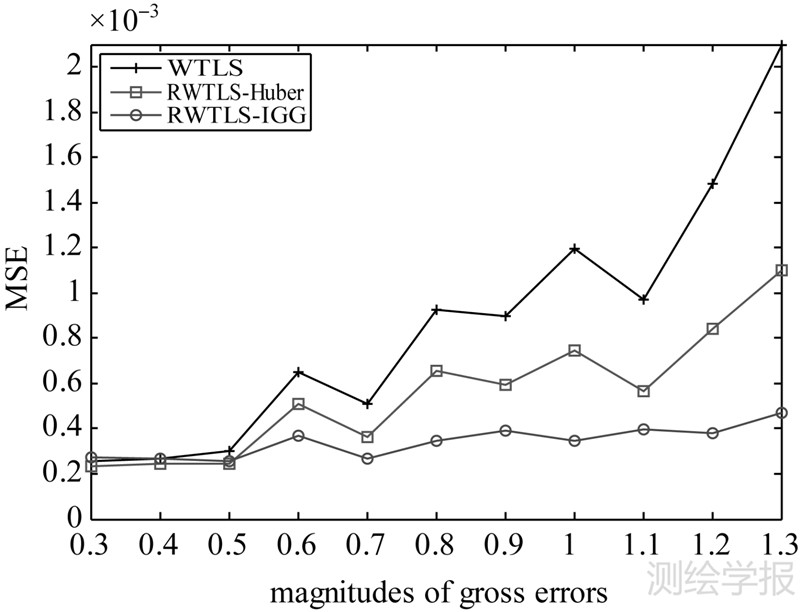
|
图 5 模拟试验中粗差大小变化时的均方误差
Fig. 5 Mean square error of estimated parameter vectors 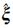 as an increase in the magnitudes of gross errors in simulation data experiment as an increase in the magnitudes of gross errors in simulation data experiment
|
根据表 1数据,分别利用WTLS方法、RWTLS-Huber方法和RWTLS-IGG方法对直线方程进行参数估计,求出参数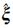 1、
1、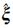 2和单位权方差
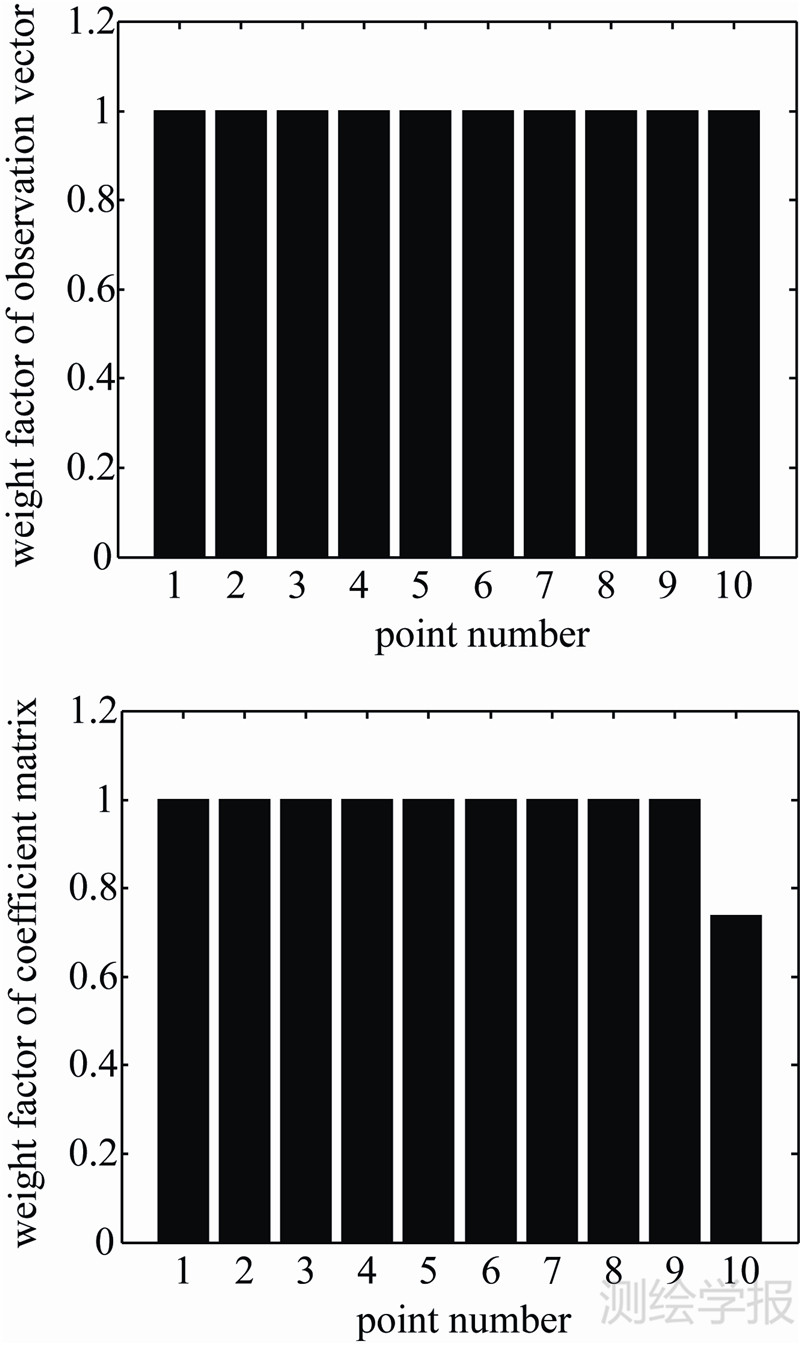
2和单位权方差 02,其结果如表 2所示。在对直线方程进行参数估计时,由于WTLS方法没有考虑数据中存在粗差的情况,其单位权方差大于其他方法,而两种稳健WTLS方法则考虑了数据中的粗差,因此所得结果更加合理。为了验证RWTLS-Huber方法对粗差的抵抗能力,作出迭代后各点的权因子图(见图 6)。
02,其结果如表 2所示。在对直线方程进行参数估计时,由于WTLS方法没有考虑数据中存在粗差的情况,其单位权方差大于其他方法,而两种稳健WTLS方法则考虑了数据中的粗差,因此所得结果更加合理。为了验证RWTLS-Huber方法对粗差的抵抗能力,作出迭代后各点的权因子图(见图 6)。
| 方法 | 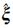 1 1 | 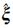 2 2 |  02 02
|
| WTLS | 5.480 | -0.481 | 1.483 |
| RWTLS-Huber | 5.455 | -0.475 | 1.456 |
| RWTLS-IGG | 5.359 | -0.453 | 1.361 |
|
| 图 6 真实试验中RWTLS-Huber方法迭代后的权因子 Fig. 6 Weight factor after iteration based on RWTLS-Huber method in real-life data experiment |
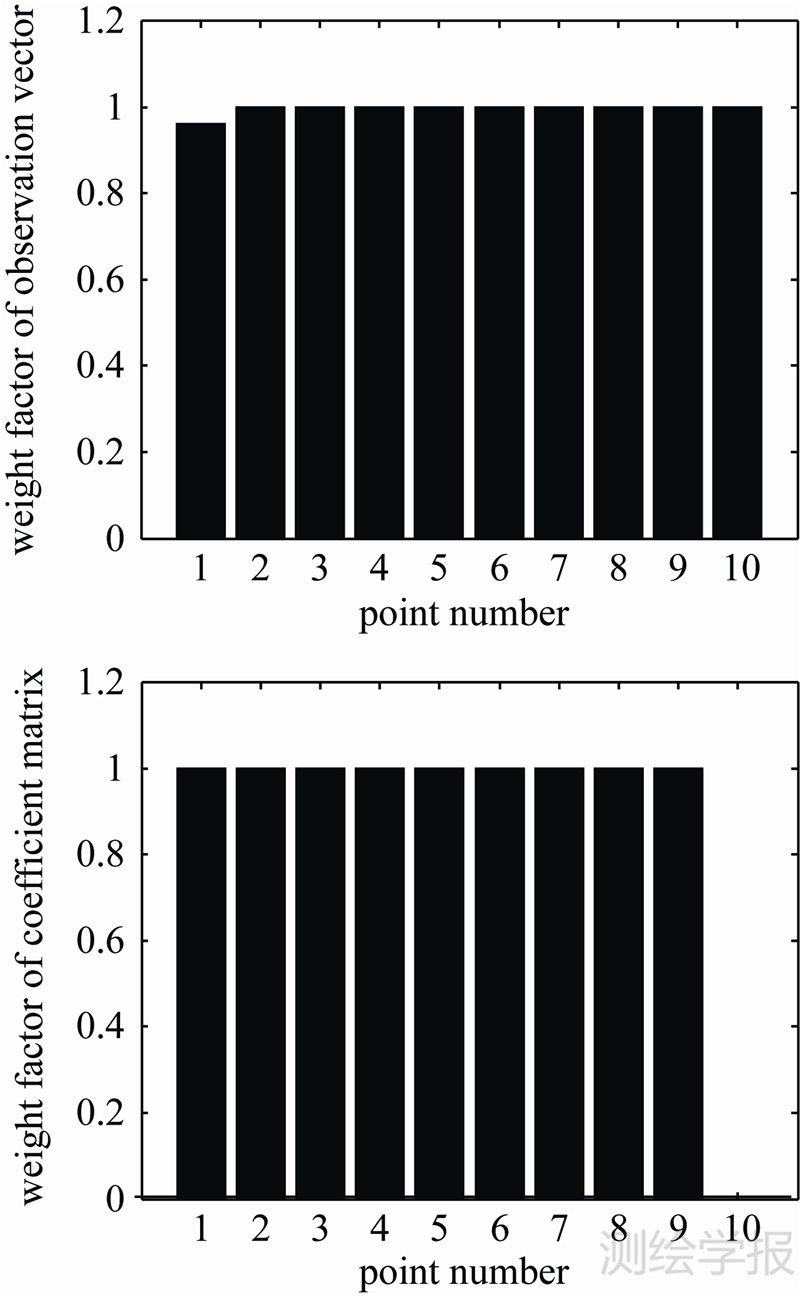
从图 6可知,RWTLS-Huber方法仅第10号点x观测数据迭代后的权因子小于1,这说明该数据可能存在粗差。为了进一步比较RWTLS-Huber方法和RWTLS-IGG方法抵抗粗差的效果,同时作出RWTLS-IGG方法迭代后各点的权因子图(见图 7)。
|
| 图 7 真实试验中RWTLS-IGG方法迭代后的权因子 Fig. 7 Weight factor after iteration based on RWTLS-IGG method in real-life data experiment |
由图 7可得,RWTLS-IGG方法第1号点y观测数据和第10号点x观测数据迭代后的权因子均小于1,且第10号点x观测数据的权因子为0,这说明他们可能存在粗差。通过对RWTLS-Huber方法和RWTLS-IGG方法迭代后权因子的比较发现,RWTLS-IGG方法探测出可能存在粗差的数据更多,所得单位权方差小于WTLS方法和RWTLS-Huber方法,说明采用RWTLS-IGG方法进行参数估计更加合理。
6 结 论在测绘实践中,可能会遇到系数矩阵含有误差的情况,如果此时采用LS方法进行参数估计显然是不恰当的。为了克服这个缺点,在顾及权矩阵的前提下,采用同时考虑观测向量和系数矩阵误差的WTLS方法被认为是更可取的。然而WTLS方法虽然考虑了系数矩阵存在随机误差的情况,但对于数据中可能存在的粗差却没有考虑,造成结果较大地偏离真实值。现有稳健加权总体最小二乘方法选取的Huber权函数缺少淘汰段,不利于提高估值的抗差能力,致使抗差效果变差。
本文通过与WTLS方法和RWTLS-Huber方法的比较表明:RWTLS-IGG方法采用IGG权函数,将系数矩阵和观测向量分别进行选权迭代,所得单位权方差和均方误差更小,且随粗差数量和粗差大小增加而增大的速度比WTLS方法和RWTLS-Huber方法要慢得多,故认为采用RWTLS-IGG方法进行参数估计的结果更加可靠。
| [1] | ZHANG Xianda. Matrix Analysis and Applications [M]. Beijing: Tsinghua University Press, 2004: 403-418.(张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 403-418.) |
| [2] | ADCOCK R. A Problem in Least Squares [J]. Analyst, 1878, 5: 53-54. |
| [3] | PEARSON K. On Lines and Planes of Closest Fit to Systems of Points in Space [J]. Philosophical Magazine and Journal of Science, 1901, 2(11): 559-572. |
| [4] | YORK D. Least-squares Fitting of a Straight Line [J]. Canadian Journal of Physics, 1966, 44(5): 1079-1086. |
| [5] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem [J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [6] | SCHAFFRIN B, SNOW K. Total Least-squares Regularization of Tykhonov Type and an Ancient Racetrack in Corinth [J]. Linear Algebra and Its Applications, 2010, 432(8): 2061-2076. |
| [7] | XU P L, LIU J N, SHI C. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis [J]. 2012, Journal of Geodesy, 86(8): 661-675. |
| [8] | LU Tieding, TAO Benzao, ZHOU Shijian. Modeling and Algorithm of Linear Regression Based on Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504-507. (鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 504-507.) |
| [9] | GONG Xunqiang, LI Zhilin. A Robust Mixed LS-TLS Based on IGGII Scheme [J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 462-466. (龚循强, 李志林. 一种利用IGGII方案的稳健混合总体最小二乘方法[J]. 武汉大学学报: 信息科学版, 2014, 39(4): 462-466.) |
| [10] | FELUS Y A. Application of Total Least Squares for Spatial Point Process Analysis [J]. Journal of Surveying Engineering, 2004, 130(3): 126-133. |
| [11] | SCHAFFRIN B, UZUN S. Errors-in-variables for Mobile Mapping Algorithms in the Presence of Outliers[C]//Proceedings of the International Symposium on Mobile Mapping Technology. Kraków: [s.n.], 2011. |
| [12] | LU Jue, CHEN Yi, ZHENG Bo. Applying Total Least Squares to Three-dimensional Datum Transformation[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 77-81. (陆珏, 陈义, 郑波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2008, 28(5): 77-81.) |
| [13] | GONG Xunqiang, CHEN Qing, ZHOU Xiufang. The Application Research of GPS Height Fitting Based on TLS Adjustment Method[J]. Bulletin of Surveying and Mapping, 2014(3): 6-8. (龚循强, 陈磬, 周秀芳. 总体最小二乘平差方法在GPS高程拟合中的应用研究[J]. 测绘通报, 2014(3): 6-8.) |
| [14] | GONG Xunqiang, LI Tong, CHEN Xijiang. Application of Total Least Squares Method in Curve Fitting[J]. Surveying and Mapping of Geology and Mineral Resources, 2012, 28(3): 4-6. (龚循强, 李通, 陈西江. 总体最小二乘法在曲线拟合中的应用[J]. 地矿测绘, 2012, 28(3): 4-6.) |
| [15] | SHEN Y, LI B, CHEN Y. An Iterative Solution of Weighted Total Least-squares Adjustment [J]. Journal of Geodesy, 2011, 85(4): 229-238. |
| [16] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression [J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [17] | FANG X. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters [J]. Journal of Geodesy, 2013, 87(8): 733-749. |
| [18] | WANG Leyang, XU Caijun. Total Least Squares Adjustment with Weight Scaling Factor[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 887-890. (王乐洋, 许才军. 附有相对权比的总体最小二乘平差[J]. 武汉大学学报: 信息科学版, 2011, 36(8): 887-890.) |
| [19] | ZHOU Yongjun, ZHU Jianjun, DENG Caihua. The Consistency between Row-wised Weighted Total Least Squares and Condition Adjustment with Parameters[J]. Acta Geodaetica et Cartographic Sinica, 2012, 41(1) : 48-53,58. (周拥军, 朱建军, 邓才华. 附参数的条件平差与按行独立的加权总体最小二乘法估计的一致性研究[J]. 测绘学报, 2012, 41(1): 48-53,58.) |
| [20] | HUBER P J. Robust Statistics [M]. Berlin: Springer, 2011. |
| [21] | NEITZEL F. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |
| [22] | CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographic Sinica, 2012, 41(5): 715-722. (陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.) |
| [23] | LU J, CHEN Y, LI B, et al. Robust Total Least Squares with Reweighting Iteration for Three-dimensional Similarity Transformation[J]. Survey Review, 2014, 46(334): 28-36. |
| [24] | QIU Weining, TAO Benzao, YAO Yibin, et al. The Theory and Method of Surveying Data Processing [M]. Wuhan: Wuhan University Press, 2008: 126-139. (邱卫宁, 陶本藻, 姚宜斌, 等. 测量数据处理理论与方法[M]. 武汉: 武汉大学出版社, 2008: 126-139.) |
| [25] | ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographic Sinica, 1989, 18(2): 115-120. (周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120.) |
| [26] | YANG Yuanxi. The Principle of Equivalent Weight: The Robust Least Squares Solution of Uniformity Model of the Parameter Adjustment[J]. Bulletin of Surveying and Mapping, 1994, 49(6): 33-35. (杨元喜. 等价权原理: 参数平差模型的抗差最小二乘解[J]. 测绘通报, 1994, 49(6): 33-35.) |
| [27] | GUI Q, Li X, GONG Y, et al. A Bayesian Unmasking Method for Locating Multiple Gross Errors Based on Posterior Probabilities of Classification Variables[J]. Journal of Geodesy, 2011, 85(4), 191-203. |