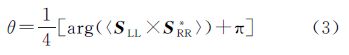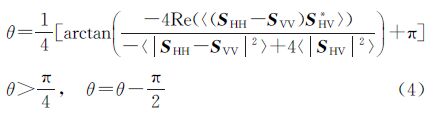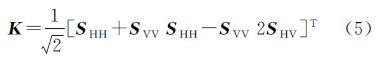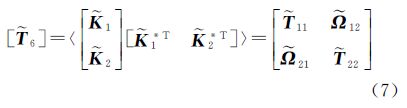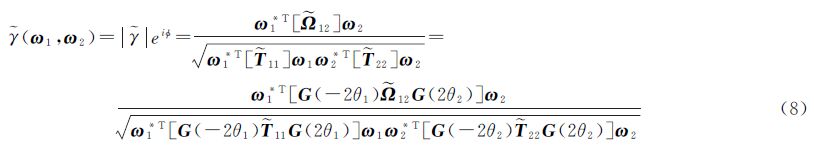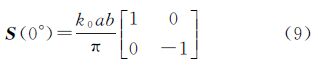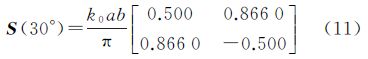2. 香港理工大学 土地测量与地理资讯学系，香港 九龙
2. Department of Land surveying and Geo-informatics, Hong Kong Polytechnic University, Hong Kong，China
电磁波的极化状态由极化方位角和椭圆角两个参数表示，极化方位角是极化椭圆的长轴和水平线的夹角。散射目标的极化方位角被认为是方位向坡度、距离向坡度和雷达入射角的函数[1]。当SAR传感器对水平地表成像，水平极化方向与地表平行，极化方位角为0°，当成像地表存在方位向和距离向的坡度，散射目标的极化方位角发生偏移。极化方位角的偏移导致散射矩阵的幅度和相位发生变化，改变散射目标的散射特性。相同散射特性的散射体由于极化方位角偏移产生不同的散射矩阵，直接影响SAR图像的分类、建筑物信息提取以及极化信息的反演[1, 2]。为了准确反演散射矩阵中包含的极化信息，文献[1, 3]提出基于外部DEM的极化方位角估计，分析了地表坡度与极化方位角的关系；文献[4]提出基于极化信号的极化方位角估计；文献[5]提出基于圆极化方法极化方位角估计；文献[1, 3]分析了极化方位角估计的特点，认为圆极化方法是比较理想的极化方位角估计方法。
极化方位角的估计与补偿已经应用于地形坡度信息反演、极化目标的识别与分类以及极化特征分解等，如文献[3]通过估计极化方位角反演了地表方位向坡度，文献[6]利用极化方位角补偿获取目标散射矩阵中的最大对称分量，文献[7]利用去极化方位角补偿将散射目标的能量集中到共极化通道，文献[8]提出多视散射矩阵和相干矩阵的极化方位角补偿方法，并应用于目标检测和极化信息分解。
极化方位角的估计与补偿对PolInSAR的复相干性估计以及植被参数反演的研究局限于模拟数据和理论分析阶段。文献[7]根据散射特性差异分析了极化方位角对PolInSAR的复相干性估计的影响，并从理论上证明了植被参数估计与极化方位角补偿的关系，并根据模拟数据分析了植被高度估计误差与极化方位角大小的关系。但是极化方位角补偿对复相干性值域以及估计方法的影响还有待进一步研究，而且，PolInSAR植被参数反演是以估计的复相干性为基础，极化方位角补偿后的复相干性对体相干性和地表相位估计的影响需要进一步明确。
本文以三阶段植被参数反演模型为基础，通过对极化SAR图像进行极化方位角估计和补偿，减弱散射目标取向差异，降低散射目标散射特性的模糊性，并建立极化方位角对极化干涉相干矩阵的补偿模型，便于准确估计植被区域的复相干性，确定体散射相位中心。以模拟数据和实际SAR分析极化方位角补偿对极化干涉相干性估计和植被参数反演的影响，研究极化方位角与复相干性估计方法的关系，明确极化方位角补偿对体散射和地表相位估计的影响程度，进一步提高植被参数反演精度。
2 极化方位角估计与补偿模型全极化SAR图像获取的2×2散射矩阵与散射目标的材质、形状和结构等物理参数相关。散射目标构造复杂性和结构空间分布差异性造成散射目标的取向差异，即引起极化SAR图像中散射矩阵极化特性的差异。极化方位角是散射目标取向的度量，认为是散射目标绕雷达视线方向的方位度量。
2.1 极化方位角的估计极化方位角可以根据外部DEM和全极化SAR 图像的散射矩阵进行估计[3, 8]。基于全极化SAR 图像散射矩阵的极化方位角的估计方法分为极化响应的方位角估计[4]，基于圆极化方法极化方位角估计[5, 9]和基于极化目标分解的极化方位角估计[10, 11]等。本文主要采用适应性较好、计算简洁的基于圆极化方法估计极化方位角。
全极化SAR数据中，散射目标在H、V线极化基下的散射矩阵S可以表示为[1]
根据极化基旋转理论，该散射目标的左旋、右旋极化基的散射矩阵Scirc可以表示为[1] 式中，SLL和SRR为左旋和右旋极化。单视或多视情况下散射目标的极化方位角可以通过SLL和SRR的相位差进行估计，极化方位角θ可以表示为[3, 8] 式中，arg表示复数的相位，SRR*表示SRR的共轭，〈·〉表示取平均运算。把式(2)代入式(3),可得基于H、V线极化基下的极化方位角θ的估计公式[3, 8, 9] 式中，Re(A)表示复数A的实部。通过式(4)估计的极化方位角的取值范围为－45°~45°。 2.2 基于极化方位角补偿的相干性估计模型
极化方位角偏移使得散射机理相同的散射目标具有不同的散射矩阵，从而导致提取的散射目标的极化信息不准确，影响散射目标的物理参数反演。极化方位角补偿是通过不同极化方位角的散射矩阵围绕雷达视线方向旋转到同一极化方位角下(如零度极化方位角)，将同一散射体具有不同极化方位角的散射矩阵变换到同一基准下，即同一散射目标在相同的散射机理下具有相同的散射矩阵，消除极化方位角对散射矩阵的影响。
散射目标的极化方位角补偿可以看作是散射目标不动，雷达视线在H、V线极化基坐标下旋转角度θ，即极化方位角补偿后的散射矩阵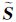
通过以旋转角度θ为参数的旋转矩阵实现[8, 9]。极化干涉SAR中的干涉矢量是以散射矩阵S为基础的Pauli基矢量K[13, 14]
为[1]
式中
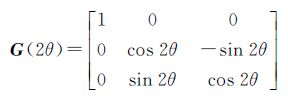
在极化干涉中两次成像时可以获取某个像元全极化散射矩阵S1和S2，分别估计S1和S2散射矩阵的极化方位角θ1和θ2，经过极化方位角补偿后的散射矩阵为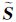1和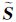2形成两个矢量1、2，半正定的赫尔默特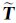
6矩阵表示为
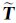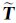11]、[22]和[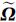
12]是3×3的复矩阵，*T表示共轭转置，其中<
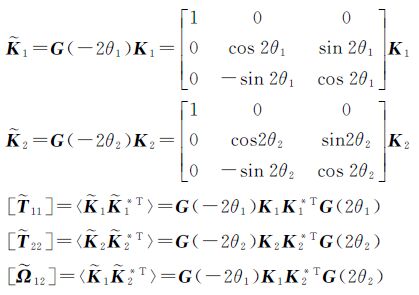
在相同的散射机制下，获取散射目标的散射矩阵会随着极化方位角偏移而变化，影响极化干涉复相干矩阵和相干性的估计。植被信息反演是以复相干性估计为基础，不同极化状态的相干性决定地表相位中心和体散射相位中心的估计。
3.1 极化方位角补偿与复相干性估计极化方位角补偿是将同一散射目标的取向归一化，即极化方位角归零化，让同一散射机制的散射矩阵不会由于极化方位角的差异导致散射矩阵的差异。理想情况下二面角在极化方位角为零时的散射矩阵可以表示为S(0°)[8]
式中，k0为波数；a和b为二面角的尺寸。根据式(5),当极化方位角为10°和30°时的散射矩阵表示为S(10°)和S(30°) 从式(10)、式(11)可以看出，极化方位角偏移使得相同散射机制下的散射矩阵存在差异，改变了散射目标的极化特性。
相同散射机制下，极化方位角偏移对散射矩阵的影响可以传递到对极化干涉复矩阵和相干性估计的影响。从式(8)中可以看出，主辅图像的极化方位角偏移促使各自散射矩阵绕雷达视线方向旋转。极化方位角补偿可以将散射矩阵归一化到零度方位角状态，准确的估计极化方位角有助于准确的估计复干涉相干性。
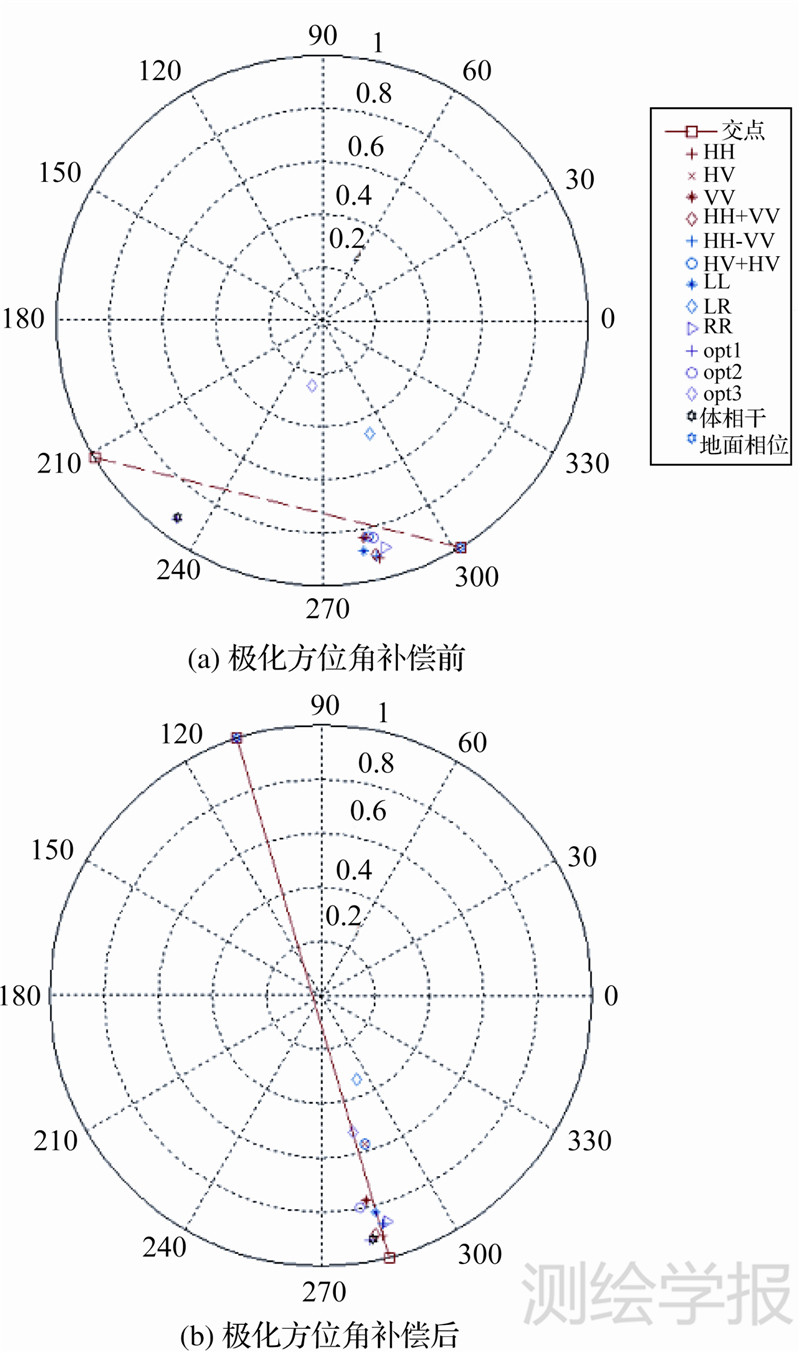
利用PolSARpro模拟的植被覆盖的全极化SAR数据，根据式(4)估计各自的极化方位角，得到极化方位角补偿后的散射矩阵。根据式(8)中复相干性估计模型，主辅影像的散射矩阵在极化方位角取值范围内以不同的组合估计极化干涉相干性，图 1为不同组合的极化方位角对相干性幅度和相位的影响。在相同的散射机制下，散射目标在主辅图像上的极化方位角对相干性的估计产生一定程度的影响。极化方位角补偿后估计相干性的幅度|r|=0.556，φ=1.183 8。未进行极化方位角补偿时，不同的极化方位角组合估计的相干性幅度变化范围为0.1~0.6，相位变化范围为－1.49~2.99。
|
| 图 1 不同极化方位角补偿对相干性的影响 Fig. 1 The influence to complex coherence by difference polarization orientation angle |
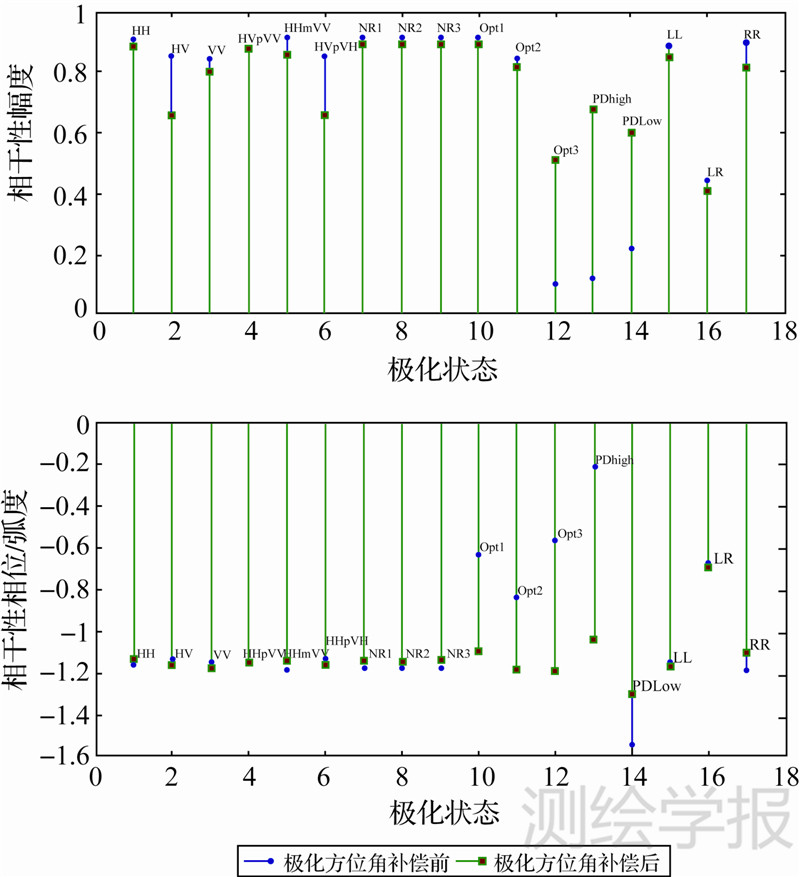
极化干涉复相干性的估计过程中，极化空间中不同极化状态对应不同的散射机制，估计的相干性幅度和相位也会不同。本文模拟植被覆盖区域的全极化数据，在9×9的估计窗口下分别估计了不同极化状态下的各种相干性。HH、HV和VV分别为线性极化的相干性，HHpVV、HHmVV和HVpVH分别为Pauli基极化的相干性，NR1、NR2和NR3为Numerical range相位中心的相干性，Opt1、Opt2 和Opt3是SVD分解方法得到的不同相位中心的相干性，PDhigh和PDlow为Phase diversity[15, 16]方法相位中心的相干性，LL、LR和RR为左右旋圆极化的相干性，图 2是不同极化状态估计的相干性分布。
|
| 图 2 极化方位角补偿对不同极化状态相干性的影响 Fig. 2 The complex coherence of difference polarization states under the influence of compensation of polarization orientation angle |
从图 2可以知道，极化方位角补偿对相干性估计方法的影响是有差异的。极化方位角补偿对Numerical range方法和圆极化方法估计的相干性影响较小，而SVD方法在相位和幅度受极化方位角补偿的影响最大。极化方位角补偿对相干性估计的影响还与散射目标的散射特性有关。植被区域散射体的取向与自然环境的影响有关，对应的体散射极化状态如HV、HVmVH和Opt3，极化方位角补偿前后相干性的幅度和相位影响较大，奇次散射和二次散射机制对应的极化状态如HH、VV和Opt1极化的相干性和相位受极化方位角补偿的影响较小。SVD方法中HHpVV极化不受极化方位角补偿的影响，与式(8)中极化方位角补偿原理一致。
3.2 极化方位角补偿与植被高度反演反演植被高信息是由体散射和地表散射的散射相位中心决定，不同散射机制下散射中心分离的准确性决定反演植被高的精度。根据三阶段法植被参数反演方法[13, 15]，不同极化状态下的相干性估计决定相干直线的估计的精度。极化方位角补偿影响相干性的估计，也会影响相干直线参数的估计。
图 3为极化方位角补偿对相干直线估计的影响，其中左图为极化方位角补偿前不同极化状态估计的相干性，红色的虚线为拟合的相干直线，右图为极化方位角补偿后不同极化状态估计的相干性，红色的实线为拟合的相干直线。极化方位角影响了部分相干性估计，不同极化状态的相干性分布符合三阶段法的线性条件。根据最小二乘原理拟合的相干直线参数受极化方位角的影响而发生改变，拟合中误差在极化方位角补偿后明显改善，提高了参数估计的可靠性。三阶段法估计的地表相位和植被高等参数与极化方位角补偿有很大关系，表 1为极化方位角补偿前后参数的估计值，极化方位角补偿后的植被高和拟合中误差与极化方位角补偿前有明显改善。
|
| 图 3 极化方位角补偿对相干直线拟合的影响 Fig. 3 The fitted coherence line affected by compensation of polarization orientation angle |
| 估计的参数 | 极化方位角补偿前 | 极化方位角补偿后 |
| 拟合中误差 | 0.217 | 0.135 |
| 地表相位 | 0.52-0.85i | -0.30+0.95i |
| 体相干 | -0.54-0.74i | 0.19-0.90i |
| 植被高/m | 40 | 25 |
极化方位角补偿是将散射矩阵的取向归一化到零度方位角，同一散射机制下散射矩阵不会因极化方位角的变化而产生差异，减弱极化方位角对极化干涉相干性的估计和植被信息反演的影响。本文选取1994年10月8日和9日美国航天飞机在贝加尔湖附近获取的L波段SIRC的全极化图像作为极化干涉的主辅图像，并进行配准、去平地效应等处理。图 4为研究区域的光学影像和Pauli基分解合成图，其中红色矩形框中为植被覆盖区域，该地区地势比较平坦，大部分植被高度为20～30 m。
|
| 图 4 研究区域Pauli基合成影像图 Fig. 4 Pauli RGB compositions on the optical image of test area |
根据式(3)、式(4)的极化方位角估计原理，采用9×9的滑动窗口依次估计每个像元的极化方位角。图 5为主辅影像估计的极化方位角。
|
| 图 5 主辅图像极化方位角估计 Fig. 5 Estimated polarization orientation of master and slave image |
主辅图像的由于时间基线和空间基线造成的散射特性差异和散射目标的取向差异都比较小，研究区域的地势起伏较小，两幅图像估计的极化方位角的分布基本相同。主辅图像散射目标的极化方位角估计后，根据式(5)计算每个像元在极化方位角补偿后的散射矩阵。通过极化方位角补偿，主辅影像中同一个散射目标的极化方位角归一化到零度方位角，消除因散射目标取向差异造成的散射性质的差异。极化方位角补偿后的散射矩阵根据式(5)构成散射矢量，通过内积形成T6矩阵，利用9×9的滑动窗口估计极化干涉相干性。本文分别估计了线性极化基、Pauli极化基、SVD分解和圆极化下的极化干涉复相干性。图 6为不同极化状态估计的极化干涉相干性。
|
| 图 6 基于极化方位角补偿估计的干涉相干性 Fig. 6 Estimated complex coherence based on the compensation of polarization orientation angle |
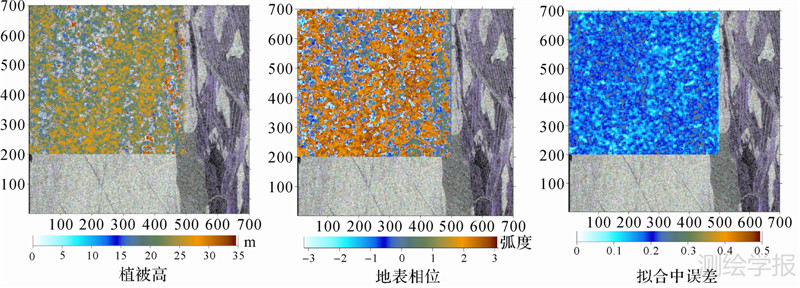
以极化方位角补偿后估计的相干性为基础，根据三阶段法植被参数反演原理，在复平面内估计每个像元的相干直线参数，确定相干直线与复平面的交点。依据极化状态的散射特性确定地表相位，以查表的方法确定SAR图像中各个像元的植被高，图 7为极化方位角补偿后的植被参数反演结果。
|
| 图 7 基于极化方位角补偿的植被参数估计 Fig. 7 Estimated forest parameters based on the compensation of polarization orientation angle |
对极化干涉SAR的主辅图像分别估计每个像元的极化方位角。表 2是估计的干涉对主辅图像极化方位角及其差分的统计表，主辅图像的极化方位角的均值和标准差为极化方位角估值的绝对值。从表中可以看出，研究区域内主辅图像估计的极化方位角差别不大，即在主辅图像中散射目标的取向有很高的相似度。
| 主图像 | 辅图像 | 极化方位角差分 | |
| 均值 | 0.29 | 0.29 | 0.02 |
| 标准差 | 0.01 | 0.02 | 0.04 |
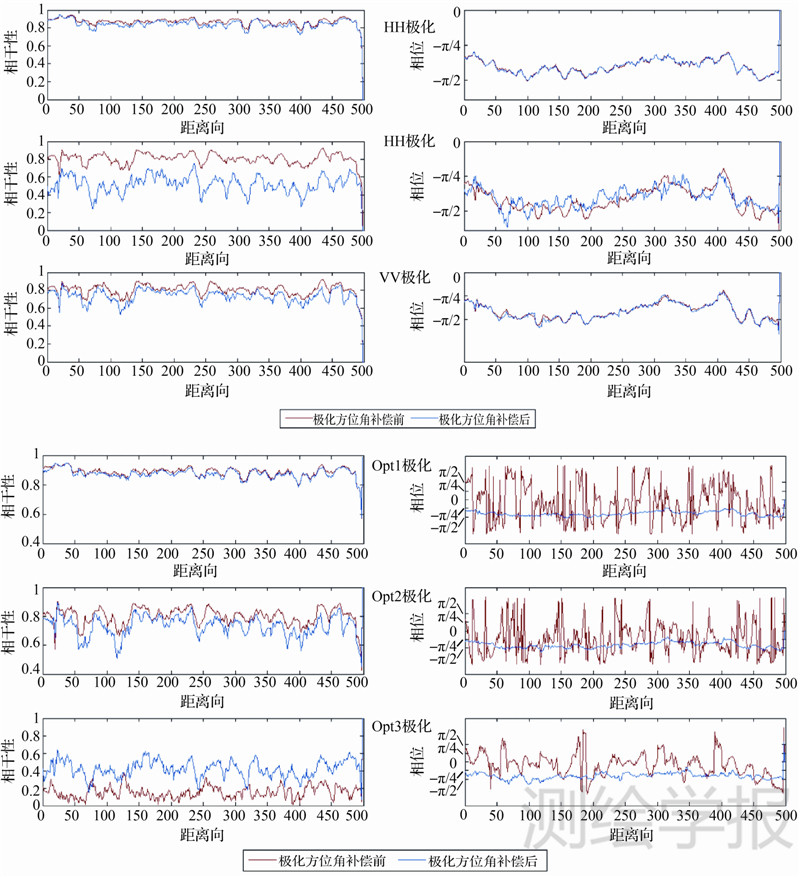
极化干涉相干性是植被参数反演的重要观测量，不同相干性估计方法估计的极化干涉相干性与极化方位角的补偿有一定的关系，特别是与体散射相关的极化状态。图 4中蓝色线段对应线性极化和SVD分解的估计相干性和相位与极化方位角补偿的关系见图 8。极化方位角补偿对HH和VV极化的相干性的相位和幅度影响很小，对体散射为主的HV极化的相干性幅度和相位的影响则很明显。SVD分解的3个相位中心对应的相干性中,极化方位角补偿对地面散射为主Opt1的相干性幅度影响很小，体散射为主的Opt3的相干性影响比较大，但是极化方位角补偿使得SVD分解的相干性相位趋于平缓。
|
| 图 8 极化方位角补偿对相干性估计方法的影响 Fig. 8 Methods of estimated coherence affected by the compensation of polarization orientation angle |
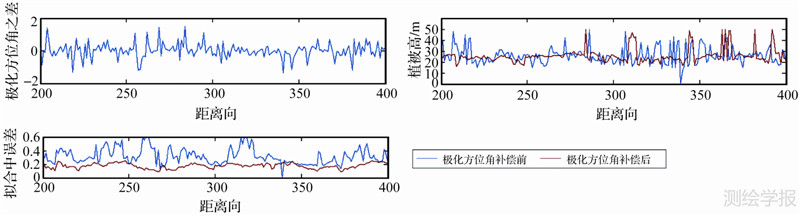
极化方位角补偿对极化干涉相干性的影响，直接表现为三阶段参数反演方法中对相干直线拟合的影响。选择研究区域中蓝色线段中的一段为剖面，极化方位角补偿对植被参数反演的影响见图 9，主辅图像的极化方位角之差趋于零，两幅图像估计的极化方位角大小基本一致。极化方位角补偿后的相干直线估计的精度与拟合中误差相关，图 9中，极化方位角补偿后的拟合中误差明显比极化方位角补偿前的要小，每个像元的相干直线拟合的精度提高，不同极化状态估计的相干性更加接近线性分布，通过极化方位角补偿后反演的植被高趋于合理，提高了反演的精度与可靠性。
|
| 图 9 极化方位角补偿对植被参数反演影响 Fig. 9 Inverted forest parameters affected by the compensation of polarization orientation angle |
表 3为极化方位角补偿前后反演的植被参数对比，极化方位角补偿前后植被高的均值没有明显的差别，但是反演的植被高标准差提高了。相干直线拟合中误差在极化方位角补偿后有明显改善，在未进行极化方位角补偿时，相干直线拟合中误差均值为0.33，还有部分像元的拟合中误差大于0.5，而在极化方位角补偿后，拟合中误差的均值和标准差都明显下降，不同极化状态估计的极化相干性分布的线性关系增强，更加符合三阶段植被高反演的假设前提，提高了植被高反演的成功率。
| 极化方位 角补偿前 | 极化方位 角补偿后 |
| 估计的 植被高/m |
|
| 拟合中 误差 |
|
| 植被高估计成功率/(%) | 70.7 | 86.0 |
极化方位角的估计与补偿影响极化特征和极化信息反演，本文针对极化方位角对散射矩阵的影响，建立多视情况下基于极化方位角补偿的极化干涉SAR相干性估计模型，分析极化方位角补偿对不同相干性估计方法和不同极化状态相干性分布的影响，通过分析及其试验对比，得出如下结论：
(1) 极化方位角影响复极化相干性的估计，在不同的最优极化相干性估计方法中，极化方位角补偿对不同性质的散射体相干性的影响程度有差异，其中对体散射估计的复相干性的幅度和相位有比较大的影响。
(2) 极化方位角补偿后复相干性可以提高相干直线的拟合精度，让不同极化状态估计的相干性分布趋向于直线，便于地表相位的确定，提高植被高估计精度。
本文中选取的数据是散射体性质比较简单，地表起伏较小的区域。但是极化方位角的估计与方位向坡度相关，不同方位向坡度和不同散射体性质下的极化方位角估计及其补偿有待进一步研究。
| [1] | LEE J S, SEHULER D L, AINSWORTH T L. Polarimetric SAR Data Compensation for Terrain Azimuth Slope Variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000,38(5):2153-2163. |
| [2] | SCHULER D L, LEE J S. Measurement of Topography Using Polarimetric SAR Images [J].IEEE Transactions on Geoscience and Remote Sensing,1996,34(5):1266-1277. |
| [3] | LEE J S, SEHULER D L, AINSWORTH T L. On the Estimation of Radar Polarization Orientation Shifts Induced by Terrain Slopes [J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(1):30-40. |
| [4] | KROGAGER E. Aspects of Polarimetric Radar Imaging[D].Denmark:Denmark University,1993. |
| [5] | CLOUDE S R, POTTIER E.A Review of Target Decomposition Theorems in Radar Polarimetry [J].IEEE Transactions on Geoscience and Remote Sensing,1996,34(3):498-518. |
| [6] | CAMERON W L, LEUNG L K. Feature Motivated Polarization Scattering Matrix Decomposition[C]//Proceedings of IEEE International Radar conference. Arlington: IEEE, 1990:549-557. |
| [7] | LI C, ZHOU Y, ZHANG Y,et al. Analysis of Terrain Influences in Pol-InSAR Forest Height Estimation and Attempts to the Correction[C]//SPIE Remote Sensing,International Society for Optics and Photonics. [S.l.]:SPIE,2012. |
| [8] | AN Wentao. The Polarimetric Decomposition and Scattering Characteristic Extraction of Polarimetric SAR[D].Beijing:Tsinghua University,2010.(安文涛.极化分解与散射特征提取研究[D].北京:清华大学,2010.) |
| [9] | CHEN Qiang, SUN Wenfeng.An Approximate Estimation of Radar Polarization Orientation Angle by Terrain Slopes [J]. Journal of Air Force Radar Academy, 2005,19(3):8-11.(陈强,孙文峰.用于地面坡度测量的极化SAR方位角近似估计方法[J].空军雷达学报,2005,19(3):8-11.) |
| [10] | WANG Chunle,YU Weidong.Comparative Analyses of Huynen Target Decomposition Methods[J].Journal of the Graduate School of the Chinese Academy of Sciences,2011,28(3):402-409.(王春乐,禹卫东. Huynen类型目标分解方法的比较与分析[J].中国科学院研究生院学报,2011,28(3):402-409.) |
| [11] | CHEN Xi, ZHANG Hong, WANG Chao. Estimation of the Polarization Orientation Angle Shifts Induced by Terrain Slopes[J].Remote Sensing Technology and Application,2007,22(1):59-64.(陈曦,张红,王超,等.由地形坡度引起的极化方位角偏移的估计[J].遥感技术与应用,2007,22(1):59-64.) |
| [12] | XU Mu, WANG Xuesong, XIAO Shunping, et al. Target Enhancement in High-resolution PolSAR Imagery Using Polarization Orientation Angle Feature [J].Signal Processing, 2008,24(1):19-23.(徐牧,王雪松,肖顺平,等.利用极化方位角特征的高分辨极化SAR目标增强研究[J].信号处理,2008,24(1):19-23.) |
| [13] | CLOUDE S,PAPATHANASSIOU K.Polarimetric SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(5): 1551-1565. |
| [14] | TAN Lulu, CHEN Bing, YANG Ruliang. Improved Three-stage Algorithm of Tree Height Retrieval with PolInSAR Data [J].Journal of System Simulation, 2010, 22(4):996-999.( 谈璐璐,陈兵,杨汝良.利用PolInSAR数据反演植被高度的改进三阶段算法[J].系统仿真学报,2010,22(4): 996-999.) |
| [15] | FLYNN T, TABB M, CARANDA R. Coherence Region Shape Extraction for Vegetation Parameter Estimation in Polarimatric SAR Interferometry[C]//Proceedings of IEEE IGARSS.Toronto:[s.n.],2002:2596-2598. |
| [16] | TABB M,ORREY J, FLYNN T,et al. Phase Diversity:A Decomposition Vegetation Parameter Estimation Using Polarimetric SAR Interferometry[C]// Proceeding of EUSAR. Cologne:[s.n.], 2002:721-724. |
| [17] | SAGUES L, LOPEZ-SANCHEZ J M, FORTUNY J,et al. Indoor Experiments on Polarimetric SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(3): 671-684. |
| [18] | NEUMANN M, REIGBER A, FERRO-FAMIL L. PolInSAR Coherence Set Theory and Appli-cation[C]//Proceedings of the European Conference on Synthetic Aperture Radar.Dresden:[s.n.],2006. |
| [19] | YANG Jie, ZHAO Lingli, SHI Lei, et al. Interpretation of Oblique Buildings Based on Optimal Polarimetric Coherence Coefficient[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(4):577-583.(杨杰,赵伶俐,史磊,等.基于最优极化相干系数的倾斜建筑解译研究[J].测绘学报,2012,41(4):577-583.) |
| [20] | LANG Fengkai,YANG Jie,ZHAO Lingli,et al. Polarimetric SAR Data Classification with Freeman Entropy and Anisotropy Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(4):556-562. (郎丰铠,杨杰,赵伶俐,等.基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J].测绘学报,2012,41(4):556-562.) |