地图的基本功能是载负和传递空间信息,合适的地图载负量是地图阅读和使用的关键[1]。近年来,地图信息量作为衡量地图复杂性程度的定量描述指标和地图载负的更优指标,成为地图学基础研究的新热点之一,可为地图设计、地图质量评价和地图空间信息传输控制提供依据[2,3,4]。
有关地图空间信息度量方法的研究较多[5,6,7,8,9],大都基于熵的概念并套用经典信息熵模型,往往忽略了地图传递信息的具体表现形式[10],因而在一定程度上缺乏客观性和合理性。近年来,学者们结合空间认知分析,发现地图信息产生于空间要素及其分布特征的多样性和差异性[11],并建立了基于空间特征的建筑物、等高线、居民点地图的空间信息度量方法[11,12,13]。与点状地图和线状地图相比较,面状地图要素及其分布的空间特征更为多样化,复杂程度差异更不均衡,进而空间信息度量考虑的因素更多,因而需要具体分析其空间特征并发展相应的空间信息度量方法。鉴于此,本文以地图上居民地为例,结合空间信息认知特点,具体分析其空间特征及其定量描述方法,发展居民地空间信息的度量方法。
2 地图信息量度量模型 2.1 基于Shannon信息熵的度量模型
在通信领域,信息被定义为随机事件的不确定性程度,Shannon在1948年发表的论文《A mathematical theory of communication》中给出了信息量的度量,即Shannon信息熵。设X为信源,也是随机变量,其可能事件发生的概率为p1、p2、…、pn,则该信源X的Shannon信息熵表达为
Shannon信息熵是事件的平均不确定性程度,其大小取决于信源的随机性程度,与事件的多样性及差异性程度无关。文献[6]提出的符号拓扑熵,文献[7]提出的拓扑和几何信息熵,文献[8]提出的几何、拓扑和专题信息熵,文献[9]提出的各种目标分布信息的度量均采用Shannon信息熵模型,并取对应特征参数的个体与总体比值作为概率来度量地图信息。然而,从人的空间认知角度,地图上要素及其分布的多样性、差异性程度越大,地图所包含的信息量越大,因此,采用这种方法度量地图信息得到的结果不符合人的认知。为此,本文采用基于特征的计算模型。
2.2 基于特征的信息量度量模型
认知是人脑的一种高级神经心理活动,通过感官感觉到事物的存在,并能对其与其他事物进行辨别,而辨别过程的实质是对特征的识别区分。地图上的要素特征越多样化,或其分布特征越多样化,可获得的信息量越大;不同的要素或不同的分布之间,差异性程度越大,则可区分性越强,从而信息量越大。据此,地图信息量度量应采用基于特征的方法[14],并采用基于特征的地图信息量计算模型[11],表达为
式中,Vi 为地图上空间与非空间特征的标准化描述指标值,对数底数为2时信息量的单位为bit。分析该计算模型可以发现:①特征的多样性程度及差异性程度直接决定信息量的大小,多样性或差异性程度越大,信息量越大;②不同对象同类型的特征,若建立统一的描述指标,则信息量度量标准相同,即相同类型的信息量具有相对可比性;③不同类型的特征,若建立统一的规范化无量纲描述指标,则不同类型的信息量具有绝对可比性。
综上可以发现,基于特征的信息量度量模型符合人对地图信息认知的规律,适合地图信息度量。采用基于特征的信息量度量模型时,地图信息量度量的关键亦转化为地图的特征分类分析与量化描述问题。为此,本文结合居民地要素及其分布的空间特征,运用层次理论,从元素层次、邻域层次和整体层次分析地图上居民地空间信息的构成,在此基础上建立各层次上空间特征的定量描述指标,并发展基于特征的居民地空间信息量度量方法。具体研究策略如图 1所示。
|
| 图 1 居民地层次空间信息度量策略 Fig. 1 The strategy of measuring the spatial information of settlements in hierarchy |
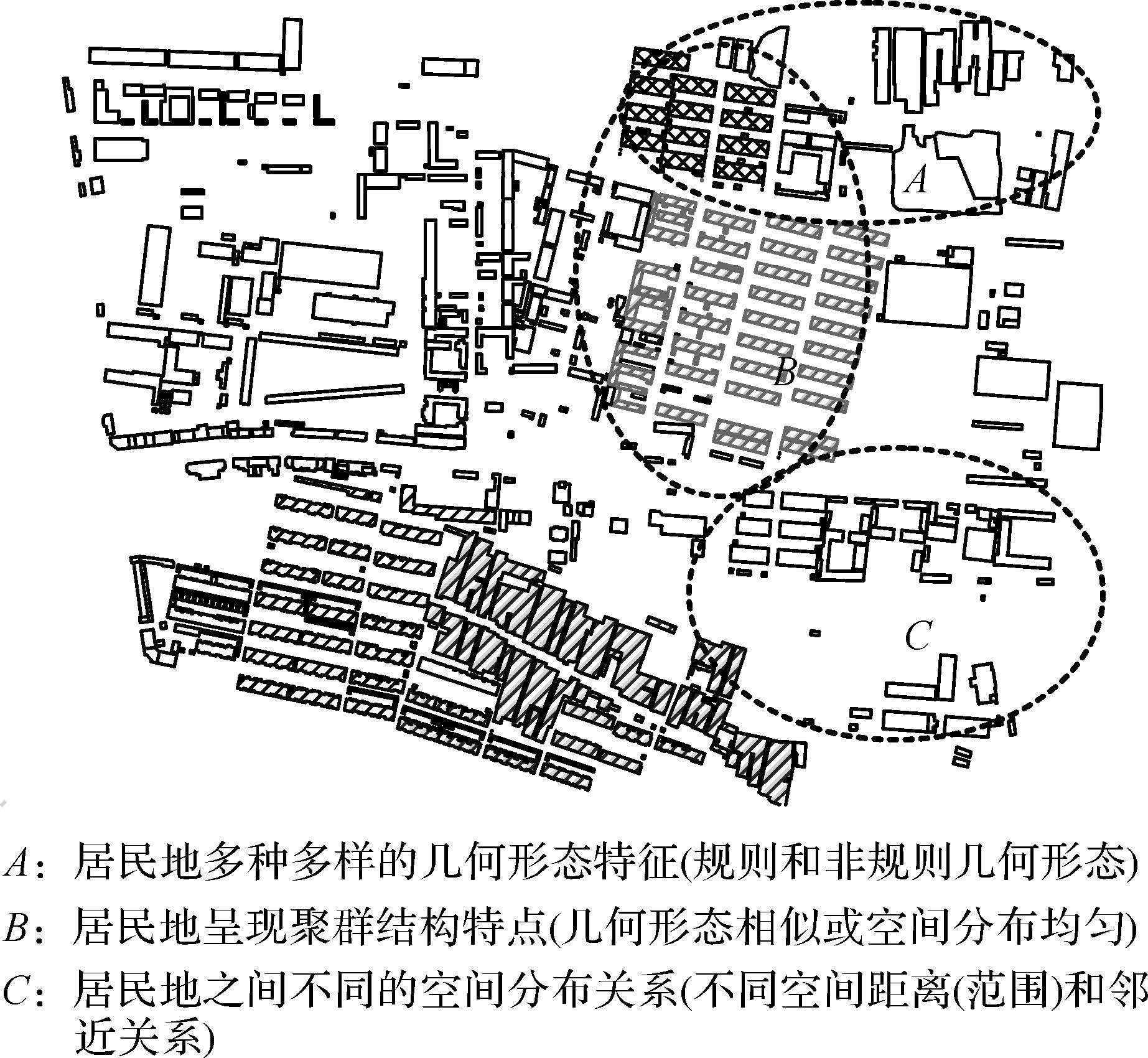
人的认知具有从宏观(或整体)到微观(或局部)的层次性特点[15,16],对地图的认知亦如此。以居民地分布图为例,整体层次关注要素分布的聚集模式特征,邻域层次关注邻近要素间的分布关系,而局部层次则关注要素的几何形态特征。以居民地专题图为例,如图 2所示,整体层次上居民地分布的聚集模式反映宏观特征,包括聚群分布范围与分布密度等;邻域层次上面要素之间的空间关系反映中观特征,包括要素之间的分离程度和连通情况;局部层次上面要素几何形态反映微观特征,包括要素的形状和尺寸。由此可见,地图上面要素及其分布的空间特征可从3个层次来描述,即元素层次的要素几何形态特征、邻域层次的邻近要素间空间关系特征和整体层次的要素聚群结构特征。
|
| 图 2 居民地空间特征 Fig. 2 Spatial characteristics of settlements |
对应于不同层次的空间特征,地图上居民地空间信息相应地由元素层次的几何形态信息、邻域层次的空间关系信息和整体层次的聚群结构信息构成。
元素层次上,居民地要素具有不同的形状和尺寸,形成几何形态的复杂多样性。边数差异、凹凸程度差异直接决定几何形态复杂程度,而尺寸的差异影响其视觉感知程度。由此可见,地图上居民地元素层次上的几何形态信息由居民地要素几何形态结构特征多样性产生,同时受面积影响[12]。
邻域层次上,居民地要素空间分布的非均匀性形成要素间复杂的空间关系,产生空间关系信息。空间关系特征的复杂性主要表现为距离关系的多样性和拓扑关系的差异性两个方面,距离关系的多样性和拓扑关系的差异性程度决定了空间关系信息量的大小。
整体层次上,居民地往往具有成群分布或区位分布的聚集特点,聚集结构分布面积较大、地物相对密集,构成所在区域的重要宏观特征[17,18]。在聚群内部,各居民地要素具有较为稳定的面积或类似的几何形态,其分布具有一定的规律性,并形成有规律的距离关系或拓扑关系,而整体上具有一定的规模、分布范围和分布密度,这种聚群结构特征的多样性和差异性产生了聚群结构信息。
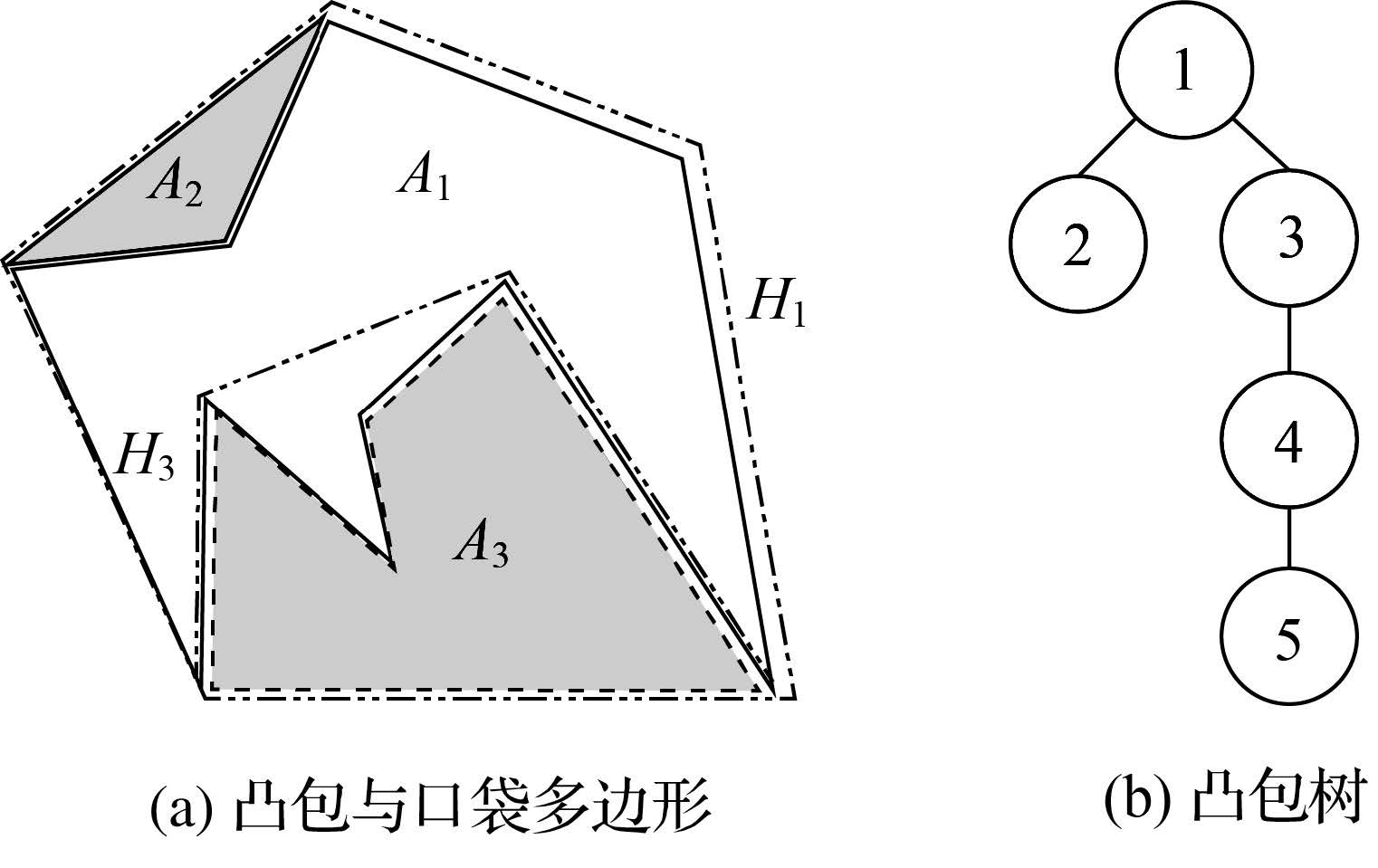
4 居民地层次空间信息的度量 4.1 元素层次居民地几何形态信息度量元素层次居民地几何形态信息由居民地几何形态的复杂多样性产生。研究表明,凸包树是符合认知的面要素几何分解表达模型[19]。仿文献[12],采用口袋多边形与凸包对作为树节点,构建单个居民地要素的凸包树。如图 3(a)所示,实线边界空心多边形表示居民地要素A1,外围的虚线边界多边形H1为A1的凸包,而点阵区域A2和A3是其口袋多边形,对应的凸包分别为A2(即为其自身)和H3;图 3(b)中所示树形结构为A1对应的凸包树。进而,复杂面要素的几何形态即可分解为凸包树节点多边形及其相互关系来描述。
多边形的几何描述参数很多,如边数、内角、边长、扁率、周长、实心度等。其中,边数是反映其几何复杂度的一个主要指标,实心度主要反映其饱和程度,节点的分布关系包括邻接关系和层级嵌套关系,表现为凸包树节点的出度和层数。据此,选取口袋多边形的边数和实心度、节点的出度和层数作为特征描述指标,同时顾及面积影响,可计算单个居民地要素Ai的几何形态信息量I(Ai)
式中,mi为Ai分解产生的凸包数;neij为凸包树节点口袋多边形边数与平均边数的比值;Cij为凸包树节点口袋多边形的实心度;lij为凸包树节点的层数与平均层数的比值;dij为凸包树节点的出度与平均出度的比值;wij为面积权,取值为凸包面积与最大凸包面积的比值。元素层次考虑要素自身几何形态,各要素几何特征之间相互独立。于是,顾及面积影响,将所有居民地要素的几何形态信息量加权求和,可得到元素层次居民地几何形态信息量Ig
式中, S为居民地要素的面积平均值;m为居民地要素总数;Wi为面积权,试验表明取要素面积与均值比时,计算结果较优。元素层次居民地几何形态信息量能够用来反映居民地几何形态复杂多样性,大比例尺地图中居民地几何细节丰富而信息量较大,并且随着比例尺缩小,居民地几何细节逐步减少,其几何形态信息量也会相应减少。
|
| 图 3 面要素的凸分解 Fig. 3 The decomposition of an area feature based on convex hulls |
邻域层次居民地空间特征主要表现为居民地分布的空间关系,这种空间关系的多样性与差异性产生空间关系信息,进而可服务于空间查询,提高查询效率。对于居民地的空间关系,人们较为关注相互邻近要素,以及邻近要素间的距离,二者分别对应两种最为典型的空间关系,即:拓扑关系和距离关系。Voronoi图是描述地图上要素空间关系的有力工具:拓扑邻接关系决定Voronoi区域公共边,邻接度即为Voronoi区域边数;邻接要素间的距离关系决定Voronoi区域扩张范围,并综合表现为Voronoi区域面积大小。面要素Voronoi区域边数越多,与之拓扑相邻的面要素亦越多,拓扑邻接关系越复杂,信息量亦越大。要素的距离关系差异越大,产生Voronoi区域面积差异越大,距离小的相互影响作用越显著,距离大的要素影响范围越大,由此产生的邻域几何分布信息量亦越大。
根据邻近要素间距离与Voronoi区域面积的关系,直接选取Voronoi区域面积描述距离关系,对其进行规范化处理后,代入式(2),可得到邻域层次由面要素距离关系产生的信息量
式中,VAreai和 VArea分别为面要素Ai对应的 Voronoi区域面积及其均值。在拓扑关系特征中,拓扑相邻关系最重要且最受关注,其中又以一阶邻接关系为主。一阶拓扑邻接度越大,面要素邻接的要素越多,拓扑关系越复杂,由此产生的信息量亦越大。因此,直接选取面要素的拓扑邻接度Adjacencyi作为拓扑关系特征描述指标,对其进行标准化后代入式(2),即得到邻域层次拓扑关系产生的信息量
式中,m为专题图上面要素的总数;Adjacency为平均拓扑邻接度。综合距离关系和拓扑关系特征产生的信息量,则可得到面状专题图邻域层次分布关系信息量
式中,INeighbor为面状专题图邻域层次分布关系信息量。 4.3 整体层次居民地聚群结构信息度量为了计算整体层次居民地聚群结构信息量,首先需要对居民地进行聚类,获得聚群结构;在此基础上,提取聚群结构的典型特征指标值,计算基于典型特征的聚群结构空间信息量。聚群结构通常表现为内部空间特征的一致性或规则性,于是,面要素的聚类方法大多是建立在形状、距离和方向的相似性度量基础上[20,21],如采用随机搜索算法的聚类、基于遗传算法的聚类、基于簇分解的聚类和顾及距离与形状相似性的聚类等方法。本文对居民地的聚类方法不展开详细讨论,试验中采用文献[21]提出的算法并结合城市形态学的思想进行聚类。
居民地数量、分布面积和密度是居民地聚群典型的特征。居民地数量 Amountk反映聚群结构的规模;分布面积反映其范围大小,可用聚群要素的 Voronoi区域总面积描述;而覆盖密度即建筑密度,是决定地价成本和居住舒适度的容积率的一个重要因子。提取聚群结构的上述3个典型空间特征的定量描述指标值,进行规范化处理后,代入式(2),即可得到聚群结构空间信息量
式中式中,k为居民地聚群的数目; SAmounti、 SAreai、 IDensityi分别为第i个聚群的居民地要素数量、 Voronoi区域总面积和覆盖密度;SAmount、SArea、SDensity为其对应的均值。
在多尺度地图表达中,需要尽量保持居民地的聚集结构模式,聚群结构信息量不会随比例尺变化而发生较大幅度变化,这个特性可用于综合算法的质量评价。
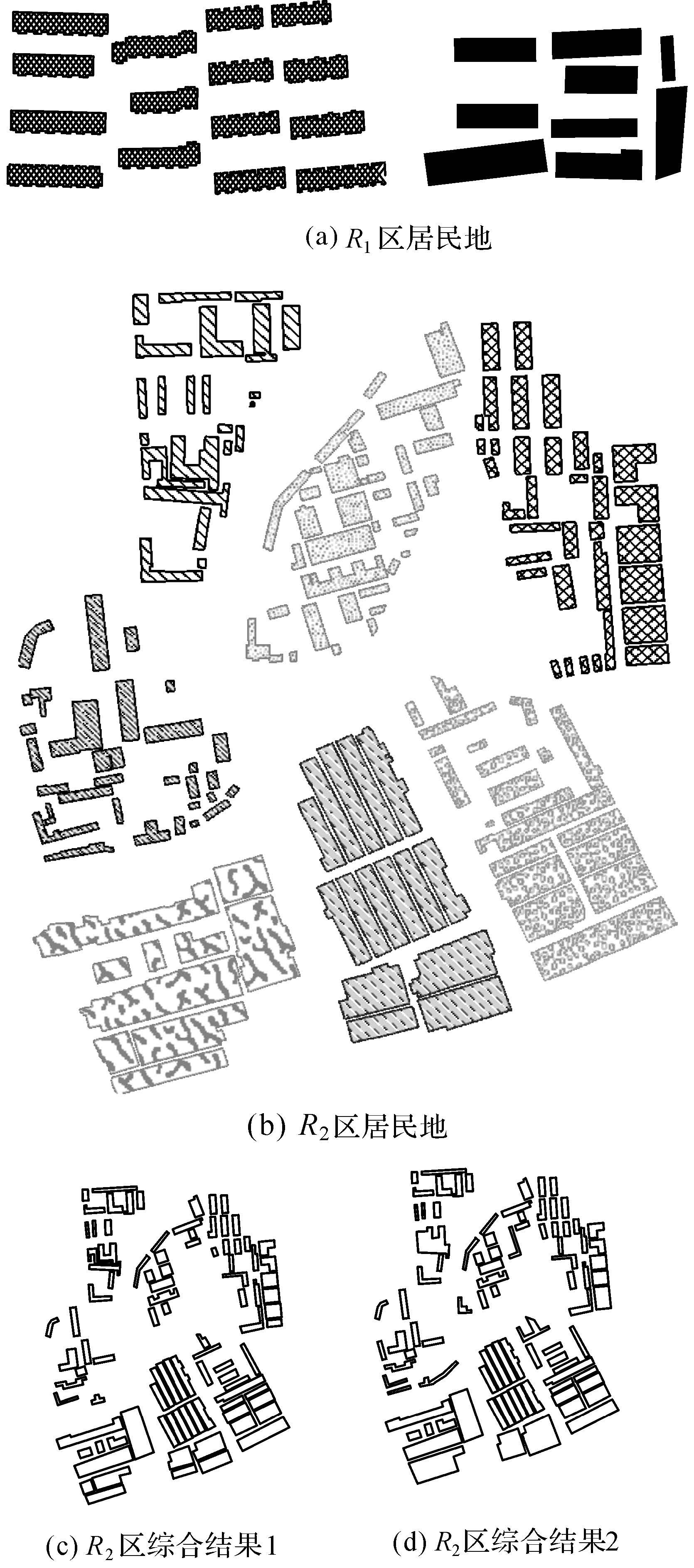
5 试验分析为了检验所提方法的合理性,本试验选取不同分布状况的两个区域居民地,采用本文方法计算居民地信息量,分别与文献[9]提出的基于统计的方法和文献[8]基于Voronoi区域划分的信息熵方法进行对比,进而运用不同综合算子对其中一个区域居民地进行综合,比较不同综合结果的层次信息量。试验数据来源于我国华东某市1∶2000的居民地地图。首先,采用顾及城市形态学改进文献[21]提出的方法进行居民地聚群,试验区居民地及其聚群划分结果如图 4(a)、图 4(b)所示,对图 4(b)中居民地综合至1∶5000得到如图 4(c)和图 4(d)所示的两个结果,其中,图 4(c)采取的综合算子主要有化简和选取,而图 4(d)采取的综合算子还包括合并和典型化。源数据的各类信息量计算结果列于表 1,综合结果的层次信息量计算结果列于表 2。
|
| 图 4 试验区居民地及其综合结果 Fig. 4 Two regions of settlements and two generalized results |
| bit | ||||
| 居民地区域 | R1 | R2 | ||
| 信 息 量 | 统计量方法 | 要素数量 | 24 | 172 |
| 要素面积 | 25983 | 64261 | ||
| 信息熵方法 | 几何信息熵 | 4.4 | 6.9 | |
| 拓扑信息熵 | 4.5 | 7.4 | ||
| 本文方法 | 几何形态信息量 | 113.1 | 607.1 | |
| 空间关系信息量 | 33.0 | 284.0 | ||
| 聚群结构信息量 | 10.0 | 46.1 | ||
| bit | ||
| 信息量 | 结果1 | 结果2 |
| 几何形态信息量 | 424.5 | 431.8 |
| 空间关系信息量 | 147.6 | 158.5 |
| 聚群结构信息量 | 44.3 | 45.8 |
分析不同方法的计算结果(表1)可以发现,本文方法计算得到的各层次信息量之间的关系及其变化趋势都比较合理,而已有方法所得到的信息量不符合认知,具体表现为:
(1) 本文方法全面考虑了居民地几何形态、分布关系和组合特征,而文献[8]基于Voronoi划分的几何、拓扑信息熵只从总体上考虑了邻近分布关系,文献[9]的统计量方法没有顾及面要素自身形态及其空间分布关系。因此,本文方法考虑的信息类型更为完整,计算得到的信息量也更为准确。
(2) 试验数据为1∶2000大比例尺数据,几何形态细节详细,因而元素层次几何形态信息量大,宏观的聚群结构信息量最小,3个层次信息量的相对大小关系合理,且反映了居民地要素及其分布特征的多样性和差异性程度。文献[8]基于Voronoi区域划分的几何、拓扑信息熵计算结果并不能真正反映居民地要素的数量特征、几何特征及其分布特征。
(3) 就不同区域居民地而言,不同层次空间特征的复杂多样性程度越大,对应的层次空间信息量越大,不同区域各层次信息量的大小关系符合认知,而文献[8]基于信息熵的方法得到结果大小失衡。
图中R1上的要素及其分布较为单一,R2上的要素及其分布复杂多样,二者的要素数量比约1∶7,占地面积比约2∶5。采用基于信息熵的方法,几何信息熵、拓扑信息熵分别为4.4、6.9和4.5、7.4,对照居民地分布状况比较其信息熵绝对量大小和相对大小,容易发现信息熵大小关系不合理。本文方法计算结果中,元素层次上,R1居民地数量及其几何形态多样性程度均明显地不及R2,因而其信息量较R2的小,但由于其中有一部分居民地要素几何形态复杂性程度较大,致使信息量比例略高于其居民地数量的比;邻域层次上,R2的空间分布关系明显比R1的复杂,因此其信息量的比例高于其居民地数量的比;整体上,R2与R1聚群数量比为7∶2,由于R2的聚群结构更多样化,分布更复杂,因此其信息量的比略高于聚群数量比。这亦表明,3个层次的信息量具有较好的独立性,并且与居民地要素及其分布的复杂多样性程度相关。
从1∶2000比例尺综合至1∶5000比例尺的居民地空间信息量(表2)可以发现,几何形态信息量有较大幅度减少,空间关系信息量有明显减少,聚群结构信息量变化不明显,但层次信息量的总体变化趋势合理。对比两种综合结果的居民地空间信息量,采用包括合并、典型化等多种综合算子得到的综合结果,与仅采用选取和化简得到的综合结果相比,其各层次信息量保持均更好。因此,从信息量保持的角度,运用多种算子的综合结果更优,而事实上运用多种综合算子的综合结果质量更好,这亦表明居民地层次空间信息量用于居民地制图综合的质量评价是可行的。
6 结 论地图信息量作为描述地图载负空间信息状况的一个度量指标,比数据量指标更为全面客观,在地图质量评价、渐进式网络地图传输、地理信息服务等方面具有广泛的应用。但是,地图空间信息量度量是一个复杂的问题,运用层次方法研究地图空间信息量的度量是一个有效途径。本文结合地图信息空间认知,通过分析面状专题图上面要素及其空间分布特征,将面状专题图的空间信息划分为元素、邻域和整体3个层次,分别建立各层次上居民地空间特征的定量描述指标,进而建立基于特征的面状专题图空间信息量度量的层次方法。试验结果表明所提出的方法具有较好的合理性与优越性。
分析发现,地图信息量大小与人的空间认知密切相关,而认知结果依赖于对特征的“识”和“别”,因而特征的合理分类和量化是信息量度量的基础。今后的研究一方面将深入探讨地图的典型空间特征选取与量化指标的优化,同时考虑要素属性或重要性程度的信息量度量方法,如考虑在Voronoi区域划分,要素信息分量中引入重要性程度加权因子等,使信息度量更精确;另一方面深入研究地图信息量度量在地图制图中的应用方法,为自动化制图提供依据和评价标准,提升地图服务质量。
| [1] | LONERGAN M, JONES C B. An Iterative Displacement Method for Conflict Resolution in Map Generalization[J].Algorithmica, 2001, 30: 287-301. |
| [2] | LIONEL G, PIERRE S, MARTINO P. Change Detection Based on Information Measure[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4503-4515. |
| [3] | SUKHOV V I. Application of Information Theory in Generalization of Map Contents[C]//International Yearbook of Cartography.London:George Philip & Son Ltd,1970:48-62. |
| [4] | WU Hehai. Research on Fundamental Theory and Technical Approaches of Automated Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 377-384. (毋河海. 地图信息自动综合基本问题研究[J]. 武汉测绘科技大学学报, 2000, 25(5): 377-384.) |
| [5] | SUKHOV V I. Information Capacity of a Map: Entropy[J]. Geodesy and Aero Photography, 1967, 10(4): 212-215. |
| [6] | NEUMANN J. The Topological Information Content of a Map: An Attempt at a Rehabilitation of Information Theory in Cartography[J]. Cartography, 1994, 31(1): 26-34. |
| [7] | BJ∅RKE J T. Framework for Entropy-based Map Evaluation[J]. Cartography and Geographical Information Systems, 1996, 23(2): 78-95. |
| [8] | LI Z L, HUANG P Z. Quantitative Measures for Spatial Information of Maps[J]. International Journal of Geographical Information Science, 2002, 16(7): 699-709. |
| [9] | HARRIE L, STIJMAR H. An Evaluation of Measures for Quantifying Map Information[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(3): 266-274. |
| [10] | CHEN Guoneng. Some Theoretical Problems of Information Science: Definition, Category and Info Flow[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2004, 43(6): 131-134. (陈国能. 信息科学的若干理论问题思考[J]. 中山大学学报:自然科学版, 2004, 43(6): 131-134.) |
| [11] | LIU Huimin, FAN Zide, DENG Min, et al. A Hierarchical Approach to Measuring the Information Content of the Contours in a Map[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 777-783. (刘慧敏, 樊子德, 邓敏, 等. 地图上等高线信息度量的层次方法研究[J]. 测绘学报, 2012, 41(5): 777-783.) |
| [12] | LIU Huimin, DENG Min, HE Zhanjun, et al. An Approach to Measuring the Spatial Information Content of an Area Feature[J] .2012,14(6): 744-750,774.(刘慧敏, 邓敏, 何占军, 等. 面要素空间信息量的度量方法研究[J]. 地球信息科学学报, 2012,14(6): 744-750,774.) |
| [13] | LIU Huimin, DENG Min, FAN Zide, et al. An Approach to Measuring the Spatial Information Content of a Point-shaped Map[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 138-144. (刘慧敏, 邓敏, 樊子德, 等. 点状地图空间信息量的度量方法研究[J]. 测绘学报, 2013, 42(1): 138-144.) |
| [14] | OU Weijun, YAO Xianlin. Measuring of Cartographic Information Amount:The General Eigen Value Measuring Method[J]. Map, 1988(4):20-24. (偶卫军, 姚贤林. 地图信息量的测度:综合特征量算法[J]. 地图, 1988(4):20-24.) |
| [15] | PALMER S. Hierarchical Structure in Perceptual Representation[J]. Cognitive Psychology, 1977, 9: 441-474. |
| [16] | BIEDERMAN I. Higher-level Vision[M]//Visual Cognition and Action: An Invitation to Cognitive Science, Cambridge:MIT Press, 1990:41-72. |
| [17] | AI Tinghua, GUO Renzhong. Polygon Cluster Pattern Mining Based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 302-308. (艾廷华, 郭仁忠. 基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3): 302-308.) |
| [18] | ZHANG Qingnian. Identification and Generalization of Spatial Structures on Map[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2002, 41(1):87-90. (张青年. 地图图形结构分析与概括研究[J]. 中山大学学报:自然科学版, 2002, 41(1):87-90.) |
| [19] | LIU H R, LIU W Y, LATECKI L J. Convex Shape Decomposition[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE, 2010: 97-104. |
| [20] | DENG Min, LIU Qiliang, LI Guangqiang, et al. Spatial Clustering Analysis and Applications[M]. Beijing: Science Press, 2011. (邓敏, 刘启亮, 李光强, 等. 空间聚类分析及应用[M]. 北京: 科学出版社, 2011.) |
| [21] | YANG Chuncheng, HE Liesong, XIE Peng, et al. Clustering Analysis of Geographical Area Entities Considering Distance and Shape Similarity[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 335-338. (杨春成, 何列松, 谢鹏,等. 顾及距离与形状相似性的面状地理实体聚类[J]. 武汉大学学报:信息科学版, 2009, 34(3): 335-338.) |