2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China
1 引 言
全球导航卫星系统(GNSS)是当今最重要的空间大地测量技术之一。导航定位和授时是GNSS的基本功能。正是由于它的精密定位功能,GNSS给大地测量带来了革命性变化,给地学的其他领域也带来了新的活力。当然,精密定位必须有精密轨道支撑,也必须有相应的软件手段。开发精密定位定轨软件,一直都受到学者们的高度重视。目前国内外已涌现诸多优秀软件,如麻省理工学院(MIT)和Scripps海洋研究所(SIO)联合研制的GAMIT/GLOBK,伯尔尼大学研制的BERNESE,喷气推进实验室(JPL)研制的GIPSY-OASIS,武汉大学研制的PANDA等。这些软件已用于IGS轨道产品的生成,有些软件还在地学界广泛应用。认识到精密定位定轨的重要性,以及自主开发相关软件的必要性,西安测绘研究所近年一直致力于GNSS定位定轨软件的研制,特别是第二作者以主要精力投入程序的编写,目前已研制成功首版卫星定位定轨系统(satellite positioning and orbit determination system,SPODS)。本文将简要介绍SPODS的基本理论及其性能测试情况,以此作为该项努力的阶段性小结。
2 理 论
|
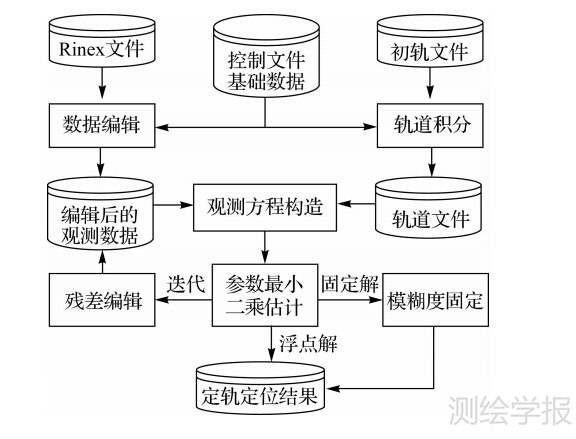
| 图 1软件结构及数据流程 Fig. 1 Software structure and data flow |
SPODS采用双频消电离层组合的非差相位和伪距作为观测量。采用TurboEdit法[1]进行相位周跳检测和修复。不可修复的周跳加以标记,在后续的参数估计过程加入模糊度参数。通过验后残差分析,进一步探测周跳和粗差。如此迭代,直至未发现新的周跳和粗差为止。
固定模糊度在双差相位上实现[2, 3, 4, 5]。参考文献[4]方法,首先依次在星座级和全网级选取独立双差模糊度,然后依据累积概率(阈值设为≥99%),序贯地将模糊度固定于最近的整数。用伪距和相位的MW组合[2],先固定宽巷模糊度,后固定窄巷模糊度。实际表明,固定模糊度会使站坐标和轨道参数的解算精度提高1~2倍[2]。
卫星轨道用初始状态向量和一组动力学模型参数描述[6]。卫星位置、状态转移矩阵和敏感矩阵在等间隔点上的值,利用Adams-Bashforth-Moulton预报校正积分器,通过数值积分得到。它们在任意时刻的值,利用拉格朗日多项式插值得到。考虑的摄动力包括:地球非球形引力、日月与行星摄动、太阳光压及相对论效应。地球引力采用12阶EGM96模型,考虑了固体潮和极潮引起的引力位变化[7],引力加速度表示为卫星坐标 x、y、z 的函数形式[6, 8]。日月与行星历表采用JPL DE405。太阳光压采用ECOM模型,用 D、Y、B 方向的常数和周期摄动加速度表示[9]。
轨道计算在地心天球参考系GCRS进行,卫星轨道产品和站坐标参考于国际地球参考系ITRS。GCRS与ITRS之间的关系用以地球定向参数为函数的旋转矩阵表示,它们之间的转换按照IERS Conventions (2003) [7]进行,岁差-章动模型采用IAU2000A[7]。EOP参数初值采用IERSA公报值,极坐标和UT1顾及了由海潮引起的周日和半周日变化,极坐标还考虑了相应于周期小于2 d的空间运动的天平动改正[7]。
观测量的改正项包括:卫星和接收机天线相位中心偏差和变化、卫星相对论钟差、对流层延迟、电离层延迟、潮汐 (固体潮、极潮和海潮负荷)位移改正。相位数据还考虑了Wind-up效应[10]改正。卫星和接收机天线相位中心偏差和变化数据取自IGS ANTEX文件,相位中心改正顾及了卫星姿态影响[11]。对流层延迟改正使用标准大气,采用Saastamoinen 天顶延迟模型和Beohm & Neill 的映射函数[12]。潮汐位移改正执行IERS Conventions (2003) [7]。
估计参数划分为全局参数和局部参数。前者包括静态测站坐标、卫星轨道参数(初始状态参数和力模型参数)、ERP参数、对流层参数(湿天顶延迟和延迟水平梯度)和模糊度参数等。后者包括动态测站(如果有的话)坐标参数和卫星与接收机钟差参数(用白噪声模型化)。参数估计采用最小二乘法。逐历元构建观测方程,组成法方程,并进行局部参数约化,将约化法方程累加到总(约化)法方程。全局参数通过总约化法方程矩阵的Cholesky分解求逆[13]得到。然后将全局参数逐历元后向回代得到局部参数,并计算验后残差。程序算法充分利用设计矩阵的稀疏特性,以求节约内存和提高计算效率。
SPODS用FORTRAN 90/95编写,约25,000行代码。
3 测试
|
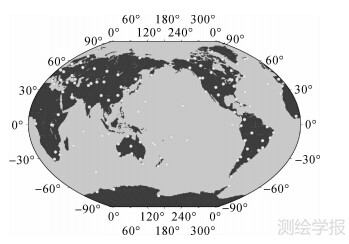
| 图 2 测试用的IGS站分布图 Fig. 2 Distribution of IGS stations used in the test |
SPODS的测试条件:
(1) 非差消电离层伪距和相位的先验误差分别取2.0 m和2 cm,按照1/sin2 E(E 为高度角)赋权,高度截止角取10°。
(2) 站坐标初值取自IGS05.SNX文件,其中10个站的每一坐标分量的先验误差取2 cm,其余站取1 km。
(3) 卫星轨道参数包括6个初始状态参数和5个光压模型参数( D0、Y0、B0、Bc和Bs) [9],它们的初值通过广播星历拟合得到。
(4) EOP先验值取自IERS A公报。估计参数包括:极坐标 xp、yp及其变率p、p,以及日长变化δ lod/lod。
(5) 每2h估计1个湿分量天顶延迟参数,每天估计1组对流层延迟水平梯度参数。
SPODS的测试结果:
下面给出SPODS的卫星轨道、站坐标和ERP参数解。值得说明,通过比较SPODS轨道和ERP解与IGS综合产品的不符值,评估前者的精度(accuracy);通过比较SPODS站坐标单日解的重复性,评估其精密度(precision)。
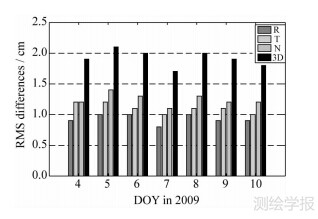
3.1 GPS轨道将卫星轨道的SPODS单日解与当周的IGS最终轨道比较,得到两种轨道的径向(R)、迹向(T)、法向(N)及三维(3D)位置的RMS差值。图 3按天号绘出所有卫星的平均RMS差。图 3显示,径向RMS差不超过1cm,迹向和法向不超过1.5cm,3D位置不超过2.5cm。关于7d的平均RMS差,3个方向依次为0.9cm,1.1cm 和1.2cm。
|
| 图 3SPODS轨道与IGS最终轨道之差的RMS 值 Fig. 3 RMS differences between SPODS orbits and final IGS orbits |
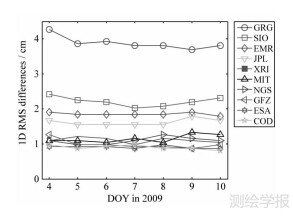
类似的,比较9个IGS分析中心的最终轨道与IGS最终轨道,得到前者与后者的1D 位置差的RMS值。图 4是10个轨道与IGS最终轨道的RMS 1D差之序列图,其中XRI标示SPODS轨道。由图看出,相对9个IGS分析中心的轨道,SPODS轨道处于相当不错的地位。
|
| 图 4 SPODS/IGS分析中心最终轨道与IGS最终轨道之差的 RMS 1D值 Fig. 4 RMS 1D differences between SPODS/IGS analysis centre orbits and final IGS orbits |
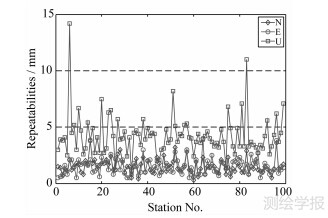
图 5绘出每天均有数据的99个站的北(N)、东(E)和上(U)分量坐标的平均日重复性。可以看出,N/E分量的重复性在5 mm以内,U分量小于10 mm (两站除外)。关于7 d的平均日重复性,3个分量分别为1.5 mm、1.5 mm和4.2 mm。
|
| 图 5 SPODS站坐标解的重复性 Fig. 5 Repeatabilities of SPODS daily solutions of station coordinates |
表 1列出SPODS的ERP日解与IGS综合产品的差值。可以看出,其差值对于 xp、yp和 δlod/lod分别不超过0.05 mas、0.12 mas和0.03 ms/d。关于7 d的RMS差,它们分别为0.025 mas、0.093 mas和0.013 ms/d。
| 2009年积日 | xp /(μas) | yp /(μas) | p /(μas/d) | p /(μas/d) | δlod/lod/(0.1 μs/d) |
| 4 | -36 | -84 | -80 | -83 | 68 |
| 5 | -9 | -96 | 127 | -102 | 149 |
| 6 | -21 | -90 | 200 | -30 | 197 |
| 7 | 18 | -93 | -3 | 95 | -72 |
| 8 | 12 | -73 | 197 | -13 | 115 |
| 9 | 29 | -115 | 162 | 45 | -10 |
| 10 | 36 | -94 | 159 | -164 | -202 |
西安测绘研究所近年一直致力于GNSS定位定轨软件的研制,目前已取得初步成果,研制成功卫星定位定轨系统SPODS第一版。利用2009年1月4日至10日大约127个IGS站的GPS数据进行的性能测试结果表明,站位置水平分量的日重复性为1.5 mm,垂直分量日重复性为4.5 mm;GPS卫星轨道与IGS最终轨道的1D差为1.1 cm。极坐标和日长变化解与IGS最终综合值分别符合至0.025 mas、.093 mas和0.013 ms/d。数据显示,目前SPODS解已具有相当好的精度水平。
下一步任务是,改进SPODS的性能,增强其功能,近期拟增加处理北斗数据的能力。
致谢: 感谢德国地学研究中心(GFZ)的葛茂荣博士,同他的讨论和交流使笔者获益颇多,特别是他对光压模型参数的意见,对软件研制起到很大作用。| [1] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letter, 1990,17(3): 199-202. |
| [2] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J]. Journal of Geophysical Research, 1989,94(B8): 10,187-110,203. |
| [3] | DONG D N,BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989,94(B4): 3949-3966. |
| [4] | GE M, GENDT G,DICK G, et al. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy,2005,79(1-3): 103-110. |
| [5] | MERVART L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D].Berne:University of Berne, 1995. |
| [6] | MONTENBRUCK O,GILL E. Saltellite Orbits Models, Methods, and Applications[M]. Berlin: Springer-Verlag, 2001. |
| [7] | MCCARTHY D D, PETIT G E. IERS Conventions (2003)[R].Frankfurt am Main:Verlag des Bundesamtes für Kartographie und Geod¨asie, 2004. |
| [8] | CUNNINGHAM L E. On the Computation of the Spherical Harmonic Terms Needed during the Numerical Integration of the Orbital Motion of an Artifical Salellite[J]. Celestial Mechanics, 1970(3): 207-216. |
| [9] | SPRINGER T A. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D]. Berne:Astronomical Institute, University of Berne, 1999. |
| [10] | WU J T,WU S C,HAJJ G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[J]. Manuscripta Geodaetic, 1993,(18): 91-98. |
| [11] | BAR-SEVER Y E. A New Model for Yaw Attitude of Global Positioning System Satellites[J]. Journal of Geodesy, 1997,70: 714-723. |
| [12] | BOEHM J, NEILL A,TREGONING P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J/OA]. Geophysical Research Letters, 2006,33(L07304). |
| [13] | BIERMAN G J. Factorization Methods for Discrete Sequential Estimation[M]. New York: Academic Press, 1977: 241. |

