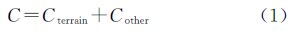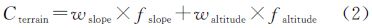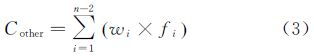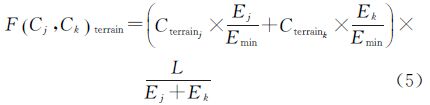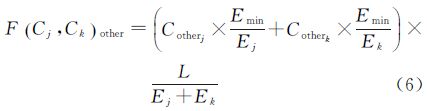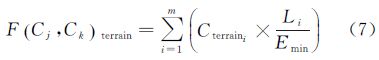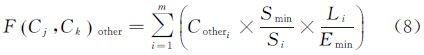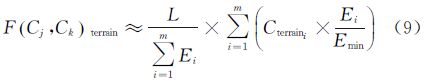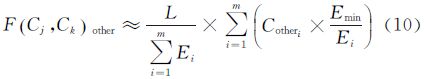2. 北京洛斯达科技有限公司,北京 100120
2. Beijing North-Star Technology Co. Ltd,Beijing 100120,China
1 引 言
路径优化是指基于某些地理数据(栅格或矢量的),给定路径的起点和终点,以及有关约束条件,计算最优(成本最低、时间最短、对环境影响最小等)线路的方法。路径优化分为两种类型,一种是在离散空间中,基于预先定义的网络数据模型,选择一条最优路径,称之为基于网络的最优路径选择,主要用于路径网络已经存在的情况,例如,研究人员基于已知网络进行网络分析[1, 2],人们在出行时经常会查询线路[3]或使用导航服务[4]。另一种是在连续空间中,基于建立的成本表面数据模型选出一条最优路径,称之为基于成本表面的路径优化,主要用于连续空间中的线路分析,例如,道路的规划[5, 6, 7, 8],输电线路的选址[9, 10],铺设天然气管线[11],有毒物质扩散路径分析,野生动物最佳迁移路径分析[12],步行路径的选择[13, 14]或运用在生态学中[15, 16, 17]等。
基于网络的最优路径选择以图论为基础,将寻找最优路径的问题转化为图搜索问题[18]。然而,图论适合解决离散数据网络的查询问题,不适合在连续空间中进行路径分析[19]。为了解决这个问题,目前在连续空间进行路径优化的常用方法是首先将这个连续空间进行栅格化,划分为相同大小的单元格,每个单元的值是经过它的成本值或困难程度,这些单元格构成了“成本表面模型”,如图 1所示;然后,根据选择的邻域模式,把成本表面中每个单元的中心或边界上的点[20]看做是节点,将每个节点与其邻域中的节点看做是有边相连,以经过的节点的成本值的和作为边的权重,这样就可以将整个成本表面当做是一个网络加权图;最后利用最优路径算法,在成本表面上就可以获得一组从起点到终点的单元格,节点连线就是规划出的最优路径。
|
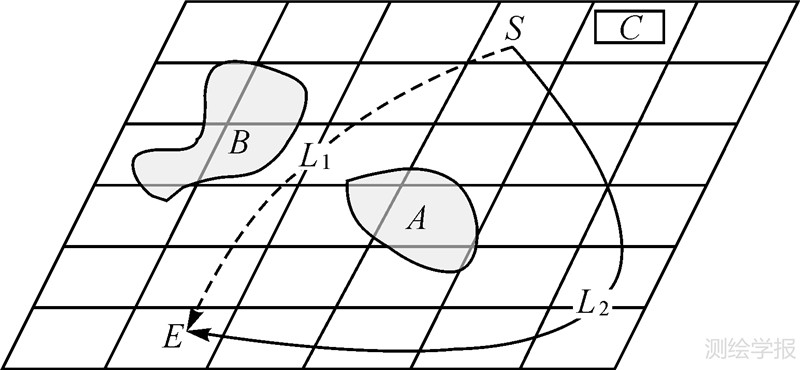
| 图 1 单分辨率成本表面模型 Fig. 1 Single resolution cost surface model |
上述过程生成的成本表面模型是规则镶嵌的栅格数据模型,它的每个单元格的大小相同,称之为单分辨率成本表面模型。单分辨率成本表面模型结构简单,易于实现,文献[5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 21, 22, 23, 24]均使用的是这种模型。但该模型不能适应它所表达的现象[25],在路径优化中使用会存在以下问题:
(1) 这种模型不能在有效表达地物密集度和地形复杂度的同时避免数据冗余。分辨率低时,不能精确表达地物密集度或地形变化度,影响计算结果的准确性。分辨率高时,虽然能表达地物的密集度或地形变化度,但会造成数据大量冗余,增加计算成本。
(2) 使用单分辨率成本表面经常会遇到图 1中的情况。图中A、B、C是3个面状地物(如林地、居民地、自然保护区等等)。S是起点,E是终点。理想的路线应该是L1,但计算机选线时往往会绕道而行,走类似L2的路径。这是由于当地物即使只覆盖单元格的一部分时,该单元格因为有了地物的成本信息而导致计算机为了降低成本绕远路,称这种现象为地物的“边缘效应”。
不规则镶嵌的方式能避免数据冗余,适应它所表达的对象[25]。文献[17, 26]采用不规则镶嵌的方式分别构建了不规则景观图和景观模型,虽然这些模型适用于生态学中,不适于路径优化,但其思想具有借鉴意义。四叉树结构[27]是不规则镶嵌中一种比较常用的方式,文献[19, 20]介绍了基于四叉树的栅格数据模型,但是对其邻域模式、成本值计算等缺乏探讨。本文在以往研究的基础上,基于四叉树数据结构的思想,采用不规则镶嵌的方式,设计了一种面向路径优化的变分辨率栅格成本表面模型。本文详细介绍了它的设计思想、邻域模式、成本值计算方式,并将其与单分变率成本表面的选线结果进行对比。
2 变分辨率栅格成本表面模型设计相对于单分辨率成本表面模型,变分辨率成本表面模型是由相互邻接、大小不同的单元格组成的。两种模型都能用于路径优化,但由于它们采用不同的镶嵌方式,继而其实现原理、单元格的邻域模式、成本值的计算方式都会有所差异。
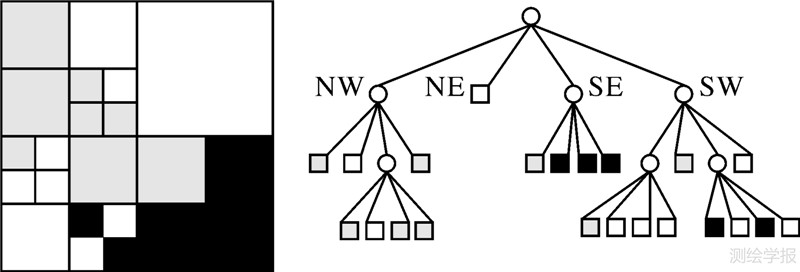
2.1 基本原理变分辨率栅格成本表面模型是基于四叉树的思想构建。四叉树是一个分层的数据结构,它不断地将那些具有多重性质的单元格四分为大小相等的子单元格,直到所有的单元格都具有唯一的性质(如该单元格只属于居民地类)。图 2[25]是一个三值的8×8的栅格层及其对应的四叉树,从四叉树图中可以看出它是先将一个连续域细分为4个子域(NW、NE、SE、SW),然后对具有多重值的子域进行不断的分割。
|
| 图 2 四叉树结构 Fig. 2 Quad trees structure |
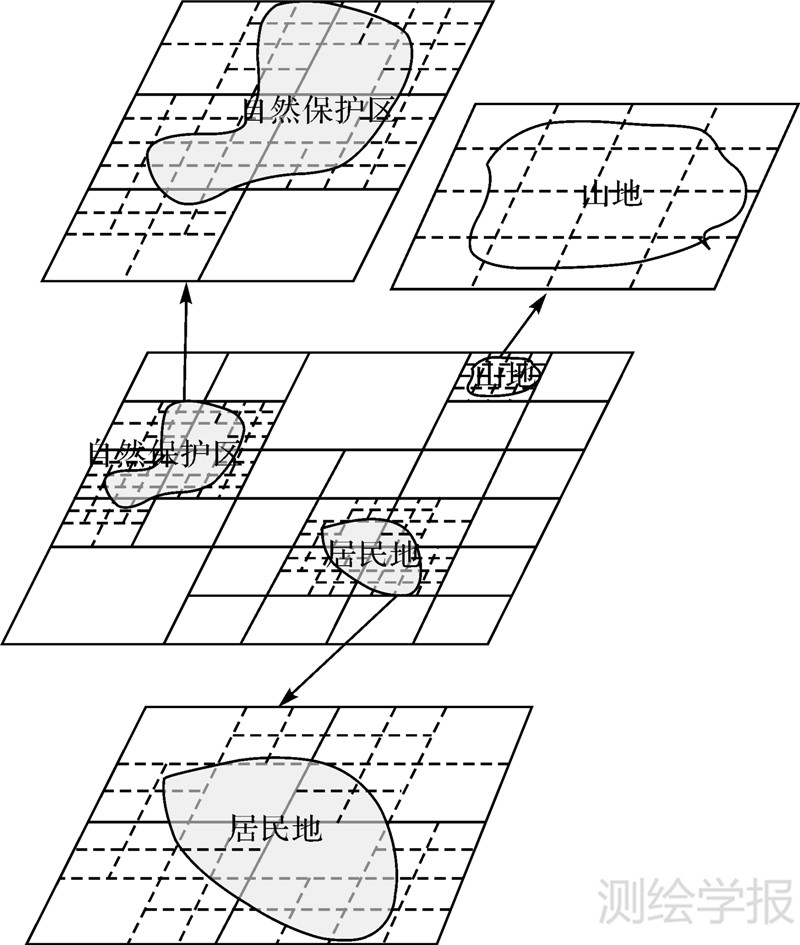
在连续空间进行路径优化需要考虑多种影响因素,如居民地、自然保护区、林地、耕地、规划区、地质情况、地形、气象区、降雨量等,将连续空间以规则镶嵌的方式栅格化后,某些因素不会完全覆盖某些单元格或者某一因素(如地形)在某些单元格内变化剧烈,这时,就以四叉树的方式来对这些单元格进行细分。例如,在地物所在的区域,对与地物边缘相交的单元格进行细分,被地物完全包含的或不与地物邻接的单元格不进行细分;在地形起伏剧烈的地区,如山地,对单元格进行细分,在地形平坦的区域不进行细分。这样在地物的边缘部分和山地的单元格就被划分得很细,能降低地物的“边缘效应”和有效表达地形复杂度,而在地物的内部、地物稀疏的部分及平坦区域的单元格被划分得较粗,避免了数据冗余。图 3即是基于这种设计思想所构造的变分辨率栅格成本表面模型。
|
| 图 3 变分辨率栅格成本表面模型 Fig. 3 Variable-resolution cost surface model |
只有成本表面,却没有指定单元格的邻域模式是不能进行路径分析的。因为这就像图搜索中只给图的节点但不给节点之间的边一样。单分辨率成本表面模型邻域模式很多,有4、8、16、32等邻域。变分辨率栅格成本表面模型的单元格大小不一,它的每个单元格的邻域包含的单元格的个数都是不确定的,因此不能像单分辨率成本表面那样以邻域中单元格的个数来区分邻域模式。
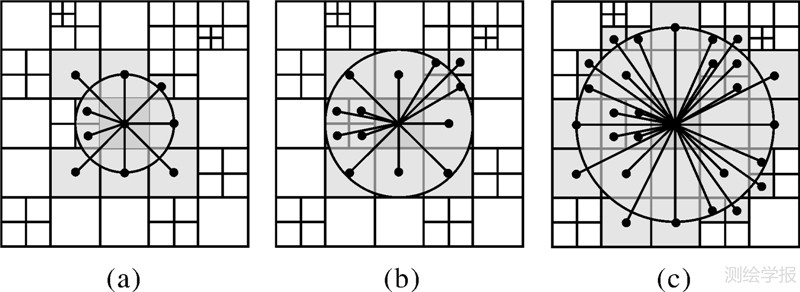
为了确定变分辨率成本表面中每个单元格的邻域,本文以半径为单元格边长的圆形区域作为该模型邻域选择的依据。如图 4所示,浅灰色单元格为深灰色单元格的邻域,图 4(a)-(c)中的浅灰色单元格分别与1倍、1.5倍、2倍边长为半径的圆内部相交。图 4(a)中的邻域单元格紧邻深灰色单元格(边缘相交),称为单层邻域,称图 4(b)、图 4(c)中的邻域为多重邻域。
|
| 图 4 变分辨率表面模型的单元格邻域模式 Fig. 4 The neighborhood pattern of variable resolution cost surface model |
成本表面模型中每个单元格都存放着经过该单元格的成本值。成本值是多种影响因素值与其相应权重的乘积之和。在路径规划中,要考虑很多种影响因素,如居民地、道路、湖泊、河流等。每种影响因素的重要性不同,需分配不同的权重。
变分辨率成本表面的单元格成本值计算较为复杂。本文将其单元格成本值C分为地形成本值Cterrain(坡度、高程变化等地形相关因素所造成的成本值)和非地形成本值Cother。C由式(1)计算。wi和fi是第i个影响因素的权重和影响因素值,n为影响因素的个数
当采用单层邻域时,单元格到其邻域的成本值F(Cj,Ck)由式(4)计算,F(Cj,Ck)terrain,F(Cj,Ck)other分别为单元格到其邻域的地形和非地形成本值。式中,Cj、Ck为单元格j、k的成本值;L为单元格j与k中心点间的空间距离;fdis为距离的权重;Emin为最小单元格的边长;Ej、Ek为单元格j和k的边长;Cterrainj、Cterraink为单元格j和k的地形成本;Cotherj、Cotherk为单元格j和k的非地形成本。
当采用多重邻域时,从Cj到Ck可能会经过m个单元格(包含Cj、Ck)。单元格到其邻域的成本值F(Cj,Ck)由式(4)计算,其中F(Cj,Ck)terrain、F(Cj,Ck)other分别由式(7)、式(8)计算。式中Li为L在单元格i上的长度,Smin表示最小单元格的面积,Si表示m个单元格中第i个的面积
由于计算Li会比较复杂,为了简化计算,可用式(9)、式(10)的结果来近似代替式(7)、式(8)
3 试验分析与应用为了测试该数据模型,选取了位于河北省承德市境内的3块不同区域作为试验数据。这3个试验区域分别是平坦区域、山地区域和平原山地混合区,具有不同的地形和不同密度的地物。这3部分试验数据包含DEM、居民地、林地、耕地、道路等数据。
在试验中,单分辨率成本表面采用8邻域模式,变分辨率成本表面采用单层邻域,使用Dijkstra算法进行路径分析。在路径分析中,主要会涉及地形、地表地物、距离3类影响因素。在地物影响因素中,居民地对通过它的路径产生的成本值(阻抗值)往往会大于湖泊或河流等所产生的(由于路径可能会对人体产生危害而遭抵制或会造成高昂的拆迁成本等),具有代表性;在地形因素中,坡度是最具代表性的。因此本文在路径分析中只考虑“居民地”、“坡度”和空间距离3种因素。试验中各因素的权重取值范围设定在[0,1]之间,各因素权值是根据选线经验多次试验得出的经验值。
3.1 地物密集的平坦区域试验分析第1个研究区域居民地密集、地形平坦,坡度对线路选址的影响可忽略不计。在该区域中线路既不能穿过居民地,又应越短越好,居民地、距离对线路的影响相当,因此坡度、居民地、距离的权值依次为0、0.5、0.5。图 5(a)中灰色多边形为居民地,灰色背景为DEM。图 5(b)-(d)以单元格成本值为背景,单元格的颜色越深成本越高。

|
| 图 5 地物密集的平坦区域选线结果 Fig. 5 Experiment results on a flat region with dense ground features |
图 5(b)中的路径是在分辨率较低的单分辨率成本表面上进行路径规划的结果,它们受到地物“边缘效应”的影响,为了避开居民地而绕的很远。图 5(c)、图 5(d)中的路径是在分辨率较高的单分辨率成本表面上和变分辨率成本表面模型上进行路径规划的结果。它们规避了地物,并且比图 5(b)中的路径短。表 1中的数据表明,图 5(d)中成本表面的单元格数量和计算成本明显低于图 5(c)中的。这说明,在平原地区,变分辨率成本表面不仅能像高分辨率成本表面那样有效表达地物的边缘部分,避免受到地物“边缘效应”的影响,而且还能避免数据冗余,降低计算成本。
| 成本表面 | 单元格数量 | 规划路径的时间/ms | |
| AB | CD | ||
| 图 5(b) | 210 | 26 | 17 |
| 图 5(c) | 14 868 | 15 948 | 14 875 |
| 图 5(d) | 3 375 | 1 624 | 1 637 |
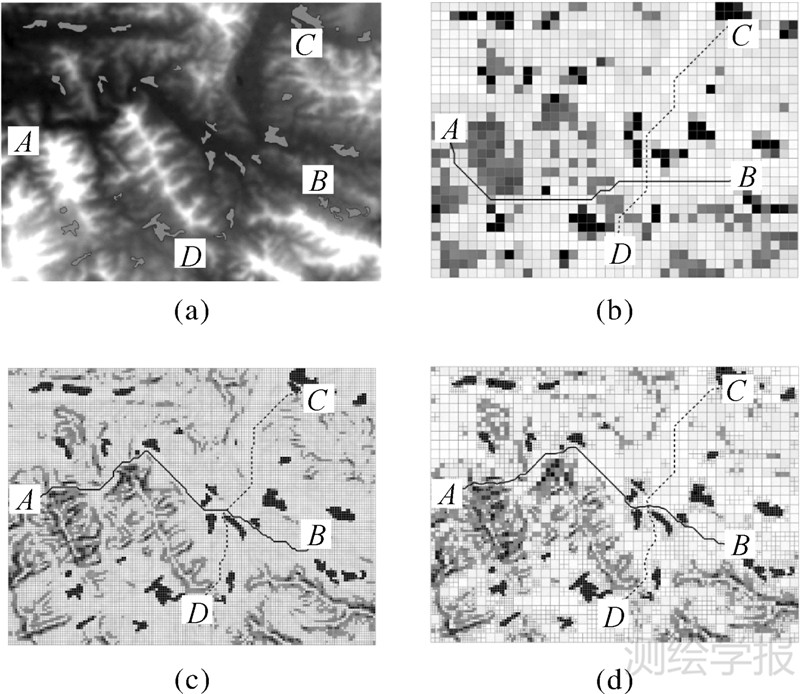
第2块试验区地形起伏较大,居民地稀疏,路径受“边缘效应”影响较小,受地形影响较大。在该区域内线路应尽量绕开坡度较大的区域,避免穿过居民地,因此坡度和居民地的权重应该赋予较大值,而距离的权重应该较小,坡度、居民地、距离的权重依次为0.5、0.4、0.1。选线的结果如图 6所示。
|
| 图 6 地物稀疏的山地的选线结果 Fig. 6 Experiment results on a mountain area with sparse ground features |
图 6(b)中的路径是在分辨率较低的单分辨率成本表面上规划出的结果,可以看出线路AB明显经过了陡峭的山地。在高分辨率成本表面上和变分辨率成本表面上规划的路径,在规避地物的同时,都绕过了坡度较大的区域,如图 6(c)、图 6(d)所示。这是因为低分辨率的成本表面不能精细表达地形复杂度,而高分辨率或变分辨率成本表面模型能有效表达地形复杂度,使选出的路径更加合理。从表 2可知,相对图 6(c)、图 6(d)中的单元格数量和计算成本更少。这说明在山地采用变分辨率成本表面模型不仅能有效表达地形复杂度,还能避免数据冗余和降低计算成本。
| 成本表面 | 单元格数量 | 规划路径的时间/ms | |
| AB | CD | ||
| 图 6(b) | 1 200 | 148 | 125 |
| 图 6(c) | 19 764 | 15 496 | 13 135 |
| 图 6(d) | 7 884 | 4 200 | 2 479 |
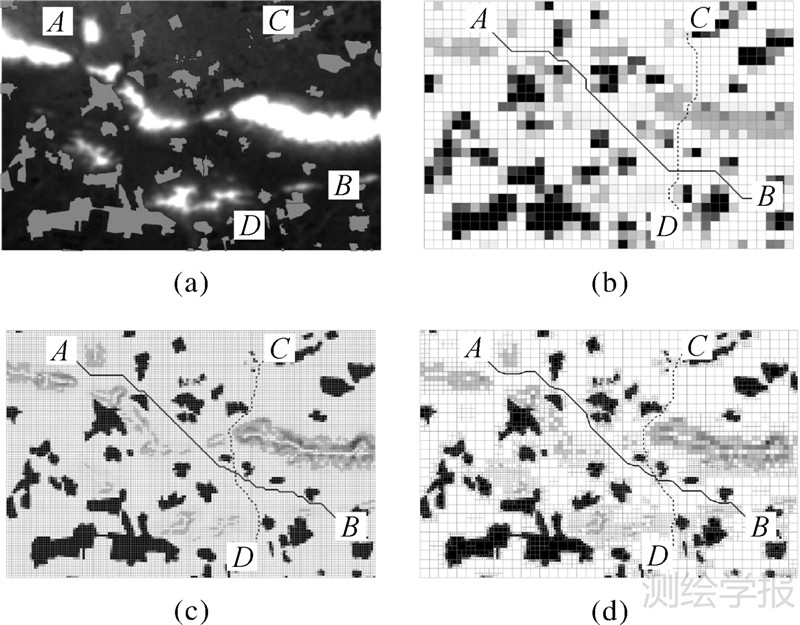
第3块区域居民地密集、平原山地皆有。在该区域选取的路径应尽量避免通过地势陡峭区域,避免穿过居民地,同时也应较多顾及空间距离因素,坡度、居民地、距离权重依次设为0.5、0.38、0.12。图 7展示了该区域内的选线结果。
|
| 图 7 地形地物复杂区域的选线结果 Fig. 7 Experiment results on an area with complex terrain and dense ground features |
该区域居民地密集,地形复杂,在低分辨率成本表面上很难得出有效路径。图 7(b)中的AB路径末端、CD路径中部与尾部都跨越了山脉。在变分辨率和高分辨率成本表面上规划出的路径较为合理,既没受到地物“边缘效应”影响也避过了地势险峻的地方,如图 7(c)、图 7(d)所示。图 7(c)、图 7(d)中的路径基本一致,但是图 7(d)中的单元格数量和计算成本明显低于图 7(c)中的,如表 3所示。这说明在地形地物复杂区域,变分辨率成本表面模型能在精确表达地形复杂度和地物密集度的同时降低数据冗余,提高计算效率。
| 成本表面 | 单元格数量 | 规划路径的时间/ms | |
| AB | CD | ||
| 图 7(b) | 1 080 | 200 | 111 |
| 图 7(c) | 17 280 | 35 196 | 15 312 |
| 图 7(d) | 7 161 | 7 972 | 4 221 |
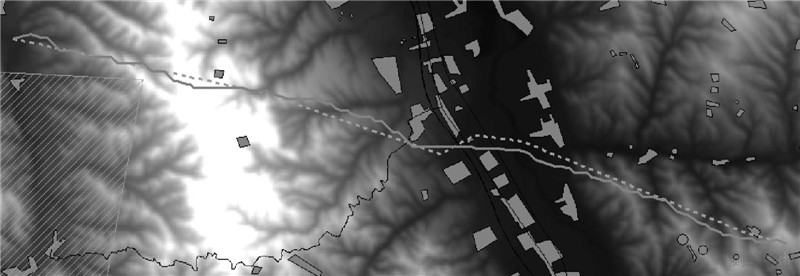
同单分辨率成本表面一样,变分辨率成本表面模型也可以应用于道路、管线、电力线路等方面路径分析。本文根据某地实际数据进行了输电线路的路径分析,将机选线路和人选线路进行对比后发现,人工线路与机选线路的最大偏离距离为400 m。这说明虽然机选线路无法替代人工选线,但机选线路可以为人工选线提供向导作用。在计算机选择出线路后,选线人员即可在其400 m的缓冲区内进行选线,而不用在长26 km、宽14 km的范围内盲选,这样能提高人工选线的速度,降低人工选线的工作量。选线结果如图 8所示,图中灰色虚线为人工选线,灰色实线为机选线路。机选线路和人工线路的偏离距离以L(单位:m)来表示,各L值所对应的部分占机选线路的长度比例如表 4所示。
|
| 图 8 机选线路与人工线路 Fig. 8 Paths routed by computer and people |
| % | |||
| 0≤L≤100 | 100<L≤200 | 200<L≤300 | 300<L≤400 |
| 35 | 24 | 24 | 17 |
面向路径优化的变分辨率栅格成本表面模型基于四叉树的思想构建,该模型能有效适应地形起伏和不同密集程度的地物。根据3个研究区域的试验结果可以得出以下主要结论:①基于该成本表面,选出的线路都是符合要求的,该成本表面能很好适用于平原、山地、地物密集或稀疏区等多种地形、地物环境;②与单分辨率成本表面相比,使用该模型进行路径优化可以在精确表达地形起伏程度、地物密集度的同时,避免数据冗余,降低计算成本;③使用该模型规划出的路径能够避免地物“边缘效应”的影响。本文虽然将变分辨率成本表面应用在电力线路的选择中,但它在诸如铁路、公路等线路的选址方面得到的应用还较少,因此,采用这种成本表面进行的选线应用依旧是下一阶段的研究重点。除此之外,在线路选址中,合适的邻域模式能有效避免线路的失真,如何扩展该模型的邻域模式也是需要关注的一个方面。
致谢:感谢北京洛斯达科技有限公司提供试验数据以及智能选线项目组成员给予的技术协作。
| [1] | WANG Jiechen, MAO Haicheng, YANG Dezhi. United Structure of Point-Arc for Network Graph and It’s Application in GISs Shortest Path Searching[J].Acta Geodaetica et Cartographica Sinica, 2000, 29(1):47-51.(王杰臣,毛海城,杨得志.图的节点-弧段联合结构表示法及其在GIS最优路径选取中的应用[J].测绘学报,2000,29(1):47-51.) |
| [2] | ZHENG Nianbo, LU Feng, LI Qingquan, et al. The Adaption of A* Algorithm for Least-time Pahts in Time-dependent Transportation Networks with Turn Delays [J]. Acta Geodaetica et Cartographica Sinica, 2010,39(5):534-539.(郑年波,陆锋,李清泉,等.顾及转向延误的时间依赖A*最短路径算法[J].测绘学报,2010,39(5):534-539.) |
| [3] | LIU B. Route Finding by Using Knowledge about the Road Network [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1997, 27(4):436-448. |
| [4] | FANG Z X, LI Q Q, ZHANG X, et al. A GIS Data Model for Landmark-based Pedestrian Navigation [J]. International Journal of Geographical Information Science, 2012, 26(5):817-838. |
| [5] | COLLISCHONN W, PILAR J V. A Direction Dependent Least-Cost-Path Algorithm for Roads and Canals [J]. International Journal of Geographical Information Science, 2000, 14(4):397- 406. |
| [6] | YU C Q,LEE J,MUNRO-STASIUK M J. Extensions to Least-Cost Path Algorithms for Roadway Planning[J].International Journal of Geographical Information Science,2003, 17(4):361-376. |
| [7] | SAHA A K, ARORA M K, GUPTA R P, et al. GIS-Based Route Planning in Landslide-Prone Areas[J]. International Journal of Geographical Information Science,2005, 19 (10):1149-1175. |
| [8] | ATKINSON D M,DEADMAN P, DUDYCHA D, et al. Multi-Criteria Evaluation and Least Cost Path Analysis for an Arctic All-Weather Road[J].Applied Geography,2005,25(4):287-307. |
| [9] | MONTEIRO C, RAMIREZ-ROSADO I J, MIRANDA V, et al.GIS Spatial Analysis Applied to Electric Line Routing Optimization[J].IEEE Transactions on Power Delivery,2005, 20(2):934-942. |
| [10] | BAGLI S, GENELETTI D,ORSI F. Routeing of Power Lines through Least-Cost Path Analysis and Multicriteria Evaluation to Minimise Environmental Impacts[J]. Environmental Impact Assessment Review, 2011,31(3):234-239. |
| [11] | LIU Xuefeng, MENG Lingkui, LI Shaohua,et al. A Cheapest Route Analysis Based on Raster GIS and Its Application[J].Bulletin of Surveying and Mapping,2004(6):43-45.(刘学锋,孟令奎,李少华,等.基于栅格GIS的最优路径分析及其应用[J].测绘通报,2004(6):43-45.) |
| [12] | QIN Kun, GUAN Zequn, LI Deren, et al. The Best Route Analysis Based on Raster Data[J].Remote Sensing for Land and Resources,2002(2):38-41.(秦昆,关泽群,李德仁,等. 基于栅格数据的最佳路径分析方法研究[J].国土资源遥感,2002(2):38-41.) |
| [13] | REES W G. Least-Cost Paths in Mountainous Terrain [J].Computers and Geosciences, 2004,30(3):203-209. |
| [14] | YAN Rui, LONG Yi, ZHENG Yue, et al. An Optimal Walking Path Algorithm Considering Terrain Influence[J].Geometics and Information Science of Wuhan University,2012,37(5): 564-569.(严瑞,龙毅,郑玥,等.顾及地形起伏的步行最优路径分析算法[J].武汉大学学报:信息科学版,2012,37(5):564-569.) |
| [15] | ADRIAENSEN F, CHARDON J P, DE BLUST G, et al. The Application of ‘Least-Cost’ Modelling as a Functional Landscape Model[J].Landscape and Urban Planning,2003, 64(4):233-247. |
| [16] | RAYFIELD B, FORTIN M J, FALL A.The Sensitivity of Least Cost Habitat Graphs to Relative Cost Surface Values[J]. Landscape Ecology,2010, 25(4):519-532. |
| [17] | ETHERINGTON T R. Least-Cost Modelling on Irregular Landscape Graphs [J].Landscape Ecology,2012,27(7):957-968. |
| [18] | MILLER H J,SHAW S L. Geographic Information Systems for Transportation[M]. Oxford: Oxford University Press,2001. |
| [19] | ANTIKAINEN H. Comparison of Different Strategies for Determining Raster-Based Least-Cost Paths with a Minimum Amount of Distortion[J]. Transactions in GIS,2013, 17(1):96-108. |
| [20] | BEMMELEN J V, QUAK W, HEKKEN M V,et al.Vector vs.Raster-Based Algorithms for Cross Country Movement Planning[R]. Hague: TNO Physics and Electronics Laboratory, 1993. |
| [21] | GONCALVES A B. An Extension of GIS-Based Least-Cost Path Modeling to the Location of Wide Paths [J]. International Journal of Geographical Information Science,2010,24(7):983-996. |
| [22] | XU J P, LATHROP R G. Improving Cost-Path Tracing in a Raster Data Format[J]. Computers and Geosciences,1994, 20(10):1455-1465. |
| [23] | XU J P, LATHROP R G. Improving Simulation Accuracy of Spread Phenomena in a Raster-Based Geographic Information System[J]. International Journal of Geographical Information Science,1995, 9(2):153 - 168. |
| [24] | DOUGLAS D H. Least-cost Path in GIS Using an Accumulated Cost Surface and Slopelines[J]. Cartographica: The International Journal for Geographic Information and Geovisualization,1994, 31(3):37-51. |
| [25] | HUISMAN O, BYROLF A D E. Principles of Geographic Information Systems[M].Enschede:ITC,2009. |
| [26] | TISCHENDORF L. Modelling Individual Movements in Heterogeneous Landscapes: Potentials of a New Approach[J]. Ecological Modelling,1997,103(1):33-42. |
| [27] | FINKEL R A,BENTLEY J L. Quad Trees: A Data Structure for Retrieval on Composite Keys[J]. Acta Informatica, 1974, 4(1):1-9. |