2. 深圳大学 海岸带地理环境监测国家测绘地理信息局重点实验室,广东 深圳 518060;
3. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079
空间辅助决策广泛应用于物流中的仓库选址、路径优化和物流监控等活动中[1]。基于地理信息技术的物流配送决策支持系统集成交通网络、仓库和客户信息,顾及容量、距离等附加约束,进行配送路线优化,设计最小费用的运输方案,辅助进行物流运营决策,提高物流效率,降低物流费用[2,3,4],其核心是高效地进行物流配送优化。
物流配送通常建模为车辆路径问题,其解空间搜索范围随客户点数量增加呈阶乘性扩大,计算时间随之急剧增长,具有典型的NP难(non-deterministic polynomial hard)特性[5],求解非常困难[6]。准确性方法只能求解不超过100个客户点的物流配送问题[7]。启发式方法能够在4h内获得3000个客户点物流配送问题的近似最优解[8]。因此需要研究更加高效的大规模物流配送优化方法。
在城市物流中,通常有多个仓库共同配送货物,满足多个客户的预订需求,一般建模为多仓库物流配送优化问题。从空间角度看,该问题包含两个空间相关的子问题:区域划分和路径优化。前者划分每个仓库的服务覆盖区域,建立仓库-客户之间的服务关系,协调仓库之间的竞争与合作,是多仓库物流配送优化的关键。直接划分方法把客户点刚性地分配给最近的仓库[9,10]。较为复杂的划分方法顾及仓库-客户服务关系的不确定性,依据概率将客户分配到某个邻近的仓库[11]。这些方法在欧式空间下建立固定的仓库-客户服务关系,将多仓库物流配送进行分解,然后进行路径优化。由于忽略了交通网络限制和仓库间的协作,设计的配送方案和现实情况存在偏差,其质量有待改善。路径优化可改变多条配送路线的片段,迭代地改善配送方案,如:变邻域搜索启发式[11]、遗传优化[9]和蚁群优化[12]等。传统路径优化方法遍历解空间,计算时间较长。空间优化策略能够有效提高优化速度,如基于空间聚类的客户点分组[13]、基于Voronoi邻域的搜索空间精简策略[14]和长边引导优化[15]。这些策略缩小局部搜索的空间范围,优化效率较高,但通常针对单仓库物流配送,需要和区域划分相配合。
从空间角度来看,多仓库物流配送优化是一个与空间要素紧密相关的优化问题。空间特性常用于设计启发式策略,快速高效地求解空间要素相关的优化问题,如:设计地理多叉树划分策略,并行优化大区域的空间资源配置[16];为保持避难所服务区域的连续性,设计基于空间邻近替换策略,进行避难所分配[17]。相关研究的启示是:根据优化问题的空间特性设计启发式优化方法。
Voronoi图根据设施的空间分布,将连续空间划分为相应的势力范围,常用于商业设施的服务区域划分[18],适合多仓库物流配送优化问题。顾及交通网络的限制,基于网络的Voronoi图更适合表达多仓库的服务区域竞争与合作[19,20,21,22]。针对多仓库物流配送,本文提出基于网络Voronoi图的启发式优化方法,进行多仓库服务区域划分与修正,并将路径优化过程限制在邻近的客户点内,快速设计大规模多仓库物流路线,在短时间内提供高质量的配送方案,减少物流费用,提高物流效率。
2 多仓库物流配送路径优化多仓库物流配送有多个仓库和客户点。每个客户均有一个非负的需求qj(j为客户点编号)。每个仓库的容量为Ci,存储客户订购的货物。每个客户点均无时间要求。多个仓库之间互相合作,共同服务于这些客户。物流车辆从某个仓库出发,服务于一定数量的客户点,并最终返回该仓库。配送方案设计若干车辆的行驶路径,以最少的耗费访问所有的客户,满足其需求。配送耗费通常以车辆数量、运输耗费(总运输距离或总运输时间)等指标度量。因此,多仓库物流配送路径优化的数学模型如下
式中,I为仓库数量;R为车辆数量;i为仓库编号,r为车辆编号。xir是0-1二进制变量,若车辆r从是从仓库i出发,并最终返回该仓库,则xir=1;否则,xir=0。Lr是车辆r访问其服务的客户点的耗费,通常为运输距离或运输时间,本文中以运输距离度量。优化目标F的第1项为车辆数量,第2项为运输耗费。K为一个极大常数,从而首先优化车辆数量。多仓库物流配送优化有以下6个约束:
(1) 客户需求不可分割。一个客户只能由一辆车服务一次,j为客户点编号,r、r′为车辆编号
(2) 每辆车最多只能使用一次
(3) 车辆装载的货物总量Qr不超过车辆容量Q
(4) 路径总长度Lr不超过车辆最大行驶距离L
(5) 仓库所服务的客户需求量之和不超过其货物储量Ci
(6) 车辆从仓库出发并返回该仓库(其中rs为车辆r出发的仓库,为re返回的仓库)
区域划分是多仓库物流配送优化的关键。该过程决定每个仓库所服务的客户需求及其位置,直接限制路径优化的方向。适应于道路网络上的受限制运动,网络Voronoi图顾及道路通行规则,更加适合表达依赖于道路网络的商业设施之间的空间竞争[19,20]。本文基于网络Voronoi图进行多仓库服务区域的初始划分,将其划分为每个仓库的占优服务空间。在仓库容量有限的情况下,货物储量不一定完全满足其Voronoi覆盖内的客户需求,初始划分需要进一步修正。通过缩小储量不足的仓库的服务区域,扩大储量丰富的仓库的服务区域,进行多个仓库之间的协作,从而满足客户需求。基于网络Voronoi图的区域划分及其修正过程如图 1所示。
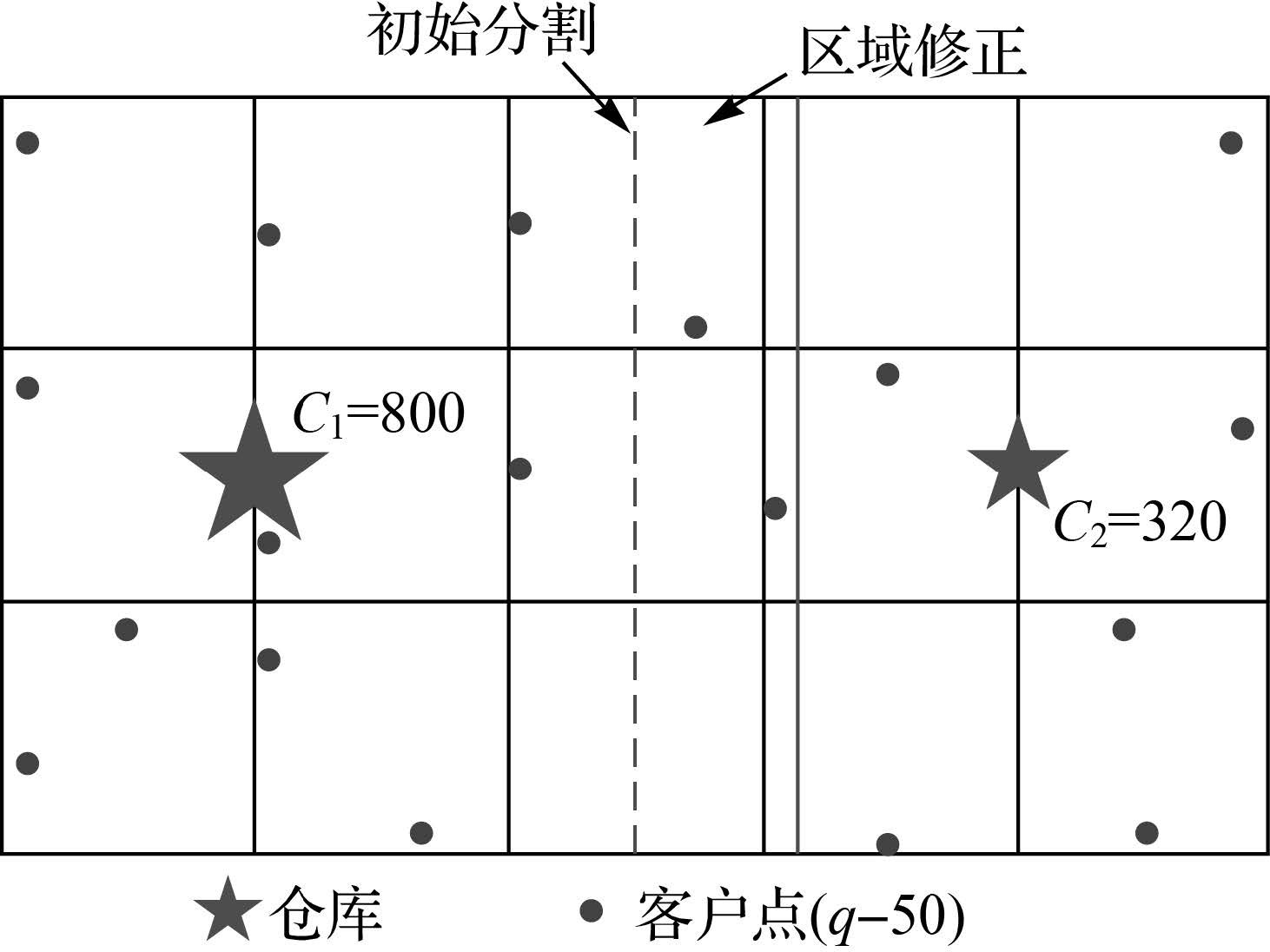
|
| 图 1 服务区域及其修正 Fig. 1 Service area and its refinement |
路径优化设计性质良好的搜索策略,在计算强度和解的质量之间取得均衡。空间邻域精简策略将搜索区域限定在一定的空间范围内,如平面K近邻[6]、平面K环Voronoi邻居[16]。由于只搜索小部分解空间,效率较高,适合大规模多仓库物流配送优化。顾及交通网络约束,本文将局部搜索范围限制在网络K近邻,保持解的质量和计算效率之间的平衡。
3 基于网络Voronoi图的大规模多仓库物流配送路径优化基于网络Voronoi图的多仓库物流配送优化设计协调处理区域划分和路径优化两个过程。区域划分过程基于网络Voronoi图进行初始分割,修正区域边界,并进行仓库-客户服务关系调整。基于空间邻近性,路径优化过程将局部搜索范围限定在网络K近邻内,从而提高优化效率。
算法流程如图 2所示,分为两个阶段:创建阶段和改善阶段。创建阶段进行服务区域初始划分并修正,创建初始解。改善阶段依次进行服务关系调整和仓库内部的路径优化,迭代改进解的质量,最终输出发现的最好解。

|
| 图 2 大规模多仓库物流配送优化方法流程 Fig. 2 The flow chart of large scale multi-depot logistics routing optimization |
区域划分将服务范围分割为各仓库的服务空间,该过程首先创建仓库的网络Voronoi面域覆盖,无缝地进行服务区域初始划分。考虑到仓库货物储量的差异,调整仓库服务区域大小。
调整过程计算每个仓库的Voronoi面域内的客户需求总和TDi,并与仓库货物储量Ci相比较,如果Ci<TDi,则进行区域边界修正。修正步骤搜索仓库i的邻近且货物富余的仓库j(Cj>TDj),将共同边界VEij向i移动,缩小仓库i的覆盖范围,从而减少其服务的需求。移动距离d逐步增大,直至式(8)成立,其中Area(VEij,d)表示i和j的共同边界VEij向仓库i移动距离d所覆盖的区域,TDArea(VEij,d)为覆盖区域内的客户需求之和
3.2 初始解创建方法服务区域划分后,每个客户被分配给其所在的仓库。多仓库物流配送被分割为多个单仓库物流配送问题。初始解创建过程逐个仓库进行。
本文采用随机插入法[24]生成每个仓库服务区域内的车辆路径,该方法能够充分利用车辆容量,使用较少车辆,且计算时间较短,适合大规模物流配送优化。随机插入法首先创建一条空的初始路径。然后,每次随机选择仓库内一个未服务的节点j,依据插入费用最小的准则,插入到顺次服务的点对(a,b)中。若未找到可行的插入位置,则创建一条新的路径,将节点j作为初始服务节点。插入费用按照式(9)计算,λ为[0.5,1.5]内的随机数
插入操作时需要满足容量约束(式(3))和距离约束(式(4))。插入节点操作反复进行,直到该仓库所服务的客户点均被安排插入到路径中的合适位置。
3.3 服务关系调整商业设施在Voronoi边界附近存在空间竞争与合作。文献[22]指出多个商业设施在服务区域边界存在侵入、互侵与邻域等竞争形态。本文将区域边界的邻近范围定义为动态区域,其大小由到边界的距离α定义。为了协调相邻仓库间的合作,服务关系调整过程利用移动节点和交换节点两个操作在动态区域内改变仓库-客户的服务关系。
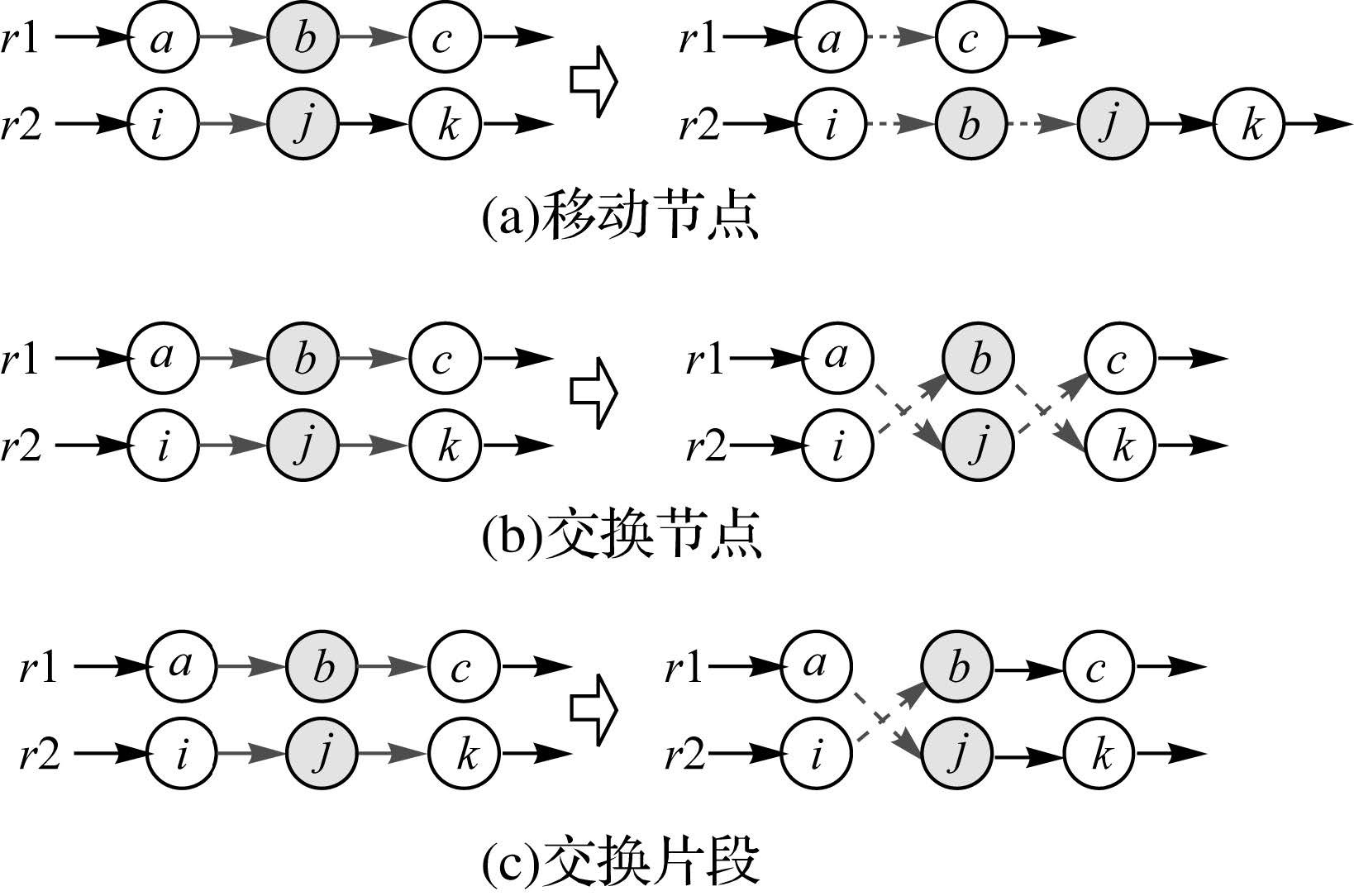
移动节点[8]将一个节点插入其他仓库服务节点的前面,如图 3(a)所示,路径长度增加值为ΔC=(dac+dib+dbj)-(dab+dbc+dij)。交换节点[8]互换两个节点的位置,如图 3(b)所示,路径长度增加值ΔC=(daj+dib+dbk+djc)-(dab+dbc+dij+djk)。移动节点和交换节点均包含两个操作参数:b和j。操作时首先选择动态区域内的一个节点作为参数b,分析其网络K近邻且由其他仓库服务的客户点j,然后选择目标函数增加值最小的节点进行。
|
| 图 3 局部搜索算子 Fig. 3 Local search operator |
服务关系调整利用上述两个算子,对动态区域内的节点逐个分析,在满足约束式(4)—(6)下,执行那些减少目标函数值的操作,从而加速路径优化过程。
3.4 路径优化过程路径优化过程对每个仓库内的路径进行局部搜索,调整路径内或路径间节点访问顺序,改善路径的质量。本文将局部搜索的空间范围限制在客户点的同一仓库服务的网络K近邻内,利用有限的计算能力只搜索那些最应该被搜索的客户节点。
本文采用3个典型的局部搜索操作[23](local search operation, LSO)搜索邻域解,包括移动节点、交换节点和交换片段。移动节点和交换节点操作如3.3节所述。交换片段操作[21]互换两条路径的尾部片段,如图图 3(c)所示,路径长度增加值为:ΔC=(daj+dibc) -(dab+dij)。
局部搜索过程通常落入局部最优解。模拟退火启发式模仿固体的冷却过程,逐渐降低温度,最终收敛于一个稳定状态。该策略能够接受一定程度的较差解,避免过早陷入局部最优,计算简单,容易实现。本文采用阈值接受准则接受较差解[6],如式(10)所示,其中f(s′)为邻域解的目标函数值,f(s)为当前最好解的目标函数值
局部搜索的操作过程如下:①随机选择一个局部搜索算子LSO;②随机选择一个客户点b;③利用LSO分析客户点b的同一仓库服务的网络K近邻,找出目标函数增加最小的节点j;④利用阈值接受准则进行判断,执行那些接受的局部操作。
每次迭代时,对于每个仓库,路径优化过程执行上述局部搜索操作3×N次(N为该仓库服务节点数量),平均每个局部搜索算子对每个节点执行一次。
3.5 时间复杂度为了分析算法的时间复杂度,假设道路网络的结构不变,即节点、路段和拓扑不变,仓库点数量I,客户点数量J,局部搜索的网络Voronoi邻近为K,动态区域的宽度为α。建立仓库网络Voronoi图的时间为T(I,J)1=O(I)[24]。客户点初始分配及调整的时间为T(I,J)2=O(IJ)。初始解遍历客户点进行插入操作,计算时间为T(I,J)3=O(J)。服务关系调整的时间为T(I,J)4=O(JαIK)。路径优化过程的时间为T(I,J)5=O(IK)。本文优化的计算总时间为T(I,J)1到T(I,J)5之和。由于多次迭代,T(I,J)1、T(I,J)2、T(I,J)3«T(I,J)4、T(I,J)5,即优化计算主要集中在服务关系调整与路径优化。综上所述,本文方法的时间复杂度为O(I+IJ+J+JαIK+IK),是客户点数量I的线性阶函数,也是仓库点数量J的线性阶函数。
4 试验与比较 4.1 试验数据与试验环境利用深圳市的导航电子地图,模拟生成多仓库物流配送问题,测试算法性能。深圳市的交通网络数据共有115904条边,84113个节点。每条边依据实际通行规则设置为单向通行和双向通行。客户点数据源于地图中的商业类兴趣点,客户点需求qj为0~100间的随机数。根据深圳市的土地利用规划,设置合理的仓库位置。从而模拟生成多仓库物流配送问题。共设计了8个不同规模的物流配送问题。客户点规模从1600到6400不等,仓库数量为2~8个。所有车辆均具有相同的容量Q=2000,最大行驶距离为L=500km。每个问题实例的具体参数如表 1所示。实例SZ1—SZ4中客户位置、仓库位置、需求大小和SZ5—SZ8中完全相同。特别的,SZ1—SZ4中货物储量充足,SZ5—SZ8中部分仓库的货物储量不充足。在试验中,以网络距离度量运输耗费,最小化使用车辆数量和路径总长度。
试验环境为台式PC,内存为4GB,CPU为Intel Core i7-3700 @3.40GHZ,操作系统环境为64位Windows 7。本文算法采用C++语言实现,为单线程执行模式。
| 问题 名称 | 客户点 数量J | 仓库数 量I | 仓库货物 储量Ci | 总需求 量TD | 容量 Q | 最大长度 L/km |
| SZ1 | 1600 | 2 | 充足 | 78967 | 2000 | 500 |
| SZ2 | 3200 | 4 | 充足 | 160677 | 2000 | 500 |
| SZ3 | 4800 | 6 | 充足 | 241497 | 2000 | 500 |
| SZ4 | 6400 | 8 | 充足 | 322056 | 2000 | 500 |
| SZ5 | 1600 | 2 | 不充足 | 78967 | 2000 | 500 |
| SZ6 | 3200 | 4 | 不充足 | 160677 | 2000 | 500 |
| SZ7 | 4800 | 6 | 不充足 | 241497 | 2000 | 500 |
| SZ8 | 6400 | 8 | 不充足 | 322056 | 2000 | 500 |
算法性能以解的质量和计算效率度量。高质量的解要求尽量使用最少的车辆,同时路径总长度尽可能少。计算效率以计算时间作为参考指标,时间越少,效率越高。
4.2 试验结果与分析经过多次试验,设定了本文算法执行时的动态区域大小α=500m,优化最大迭代次数Imax=2000,网络K近邻K=30。每个问题实例运行算法3次,记录最好解的车辆数量、路径总长度和计算时间。
表2统计8个多仓库物流配送问题的计算结果。由表可知,本文算法在较快时间内生成了初始解。从解的质量上看,相对于初始解,经过服务关系调整和路径优化后,解的质量得到了明显提升。初始解生成时间较短,在规模最大的实例SZ8上,本文算法在82.4 s内生成了初始解。在使用车辆数量上,初始解的路径数量已经较少,实例SZ1、SZ2、SZ5、SZ6的初始方案和最终方案一致。在SZ3、SZ4、SZ7、SZ8上,最终方案使用的车辆数量均有所减少。8个实例使用的车辆数量和从820减少到810,略高于理论上的最小值(808)。在路径长度上,最终方案的路径总长度约为初始方案的24.1%。和货物充足的问题SZ1—SZ4比较,SZ5—SZ8的算法性能大致相同。综上所述,基于网络Voronoi图的启发式优化方法能够大幅度改善初始解的质量。
在计算效率上,本文算法在867.8s内给出了6400个客户点的实例SZ8的解,用时较少。计算时间随客户点数量增长较为缓慢。如表 2所示,以实例SZ1为基准,SZ4的客户点增长了4倍,其计算时间约增长了7.2倍,增长速度略高于线性增长,和理论分析结果基本一致。
| 问题实例 | 客户数量 J |  |
初始方案 | 最终方案 | ||||||
| 路径数量 R0 | 路径总长度 L0/km | 创建时间 T0 | 路径数量 R1 | 路径总长度 L1/km | 改善幅度 gap/(%) | 计算时间 T1 | ||||
| SZ1 | 1600 | 40 | 40 | 9543.185 | 14.9 | 40 | 2083.728 | 21.8 | 118.7 | |
| SZ2 | 3200 | 81 | 81 | 13695.007 | 32.4 | 81 | 3150.316 | 23.0 | 310.8 | |
| SZ3 | 4800 | 121 | 123 | 15408.020 | 49.2 | 121 | 4051.624 | 26.3 | 562.2 | |
| SZ4 | 6400 | 162 | 166 | 17725.300 | 80.3 | 162 | 4749.621 | 26.8 | 850.5 | |
| SZ5 | 1600 | 40 | 40 | 9645.723 | 15.2 | 40 | 2114.839 | 21.9 | 125.3 | |
| SZ6 | 3200 | 81 | 81 | 13950.001 | 34.5 | 81 | 3157.755 | 22.6 | 322.3 | |
| SZ7 | 4800 | 121 | 123 | 15962.817 | 54.6 | 122 | 4066.205 | 25.5 | 576.3 | |
| SZ8 | 6400 | 162 | 166 | 19276.298 | 82.4 | 163 | 4850.447 | 25.2 | 867.8 | |
| 路径数量和 | 808 | 820 | 810 | |||||||
| 平均改善幅度 | 24.1 | |||||||||
| 平均计算时间 | 466.7 | |||||||||
注: 为理论上最少使用的车辆数。改善幅度gap= L1/L0×100% 为理论上最少使用的车辆数。改善幅度gap= L1/L0×100% | ||||||||||
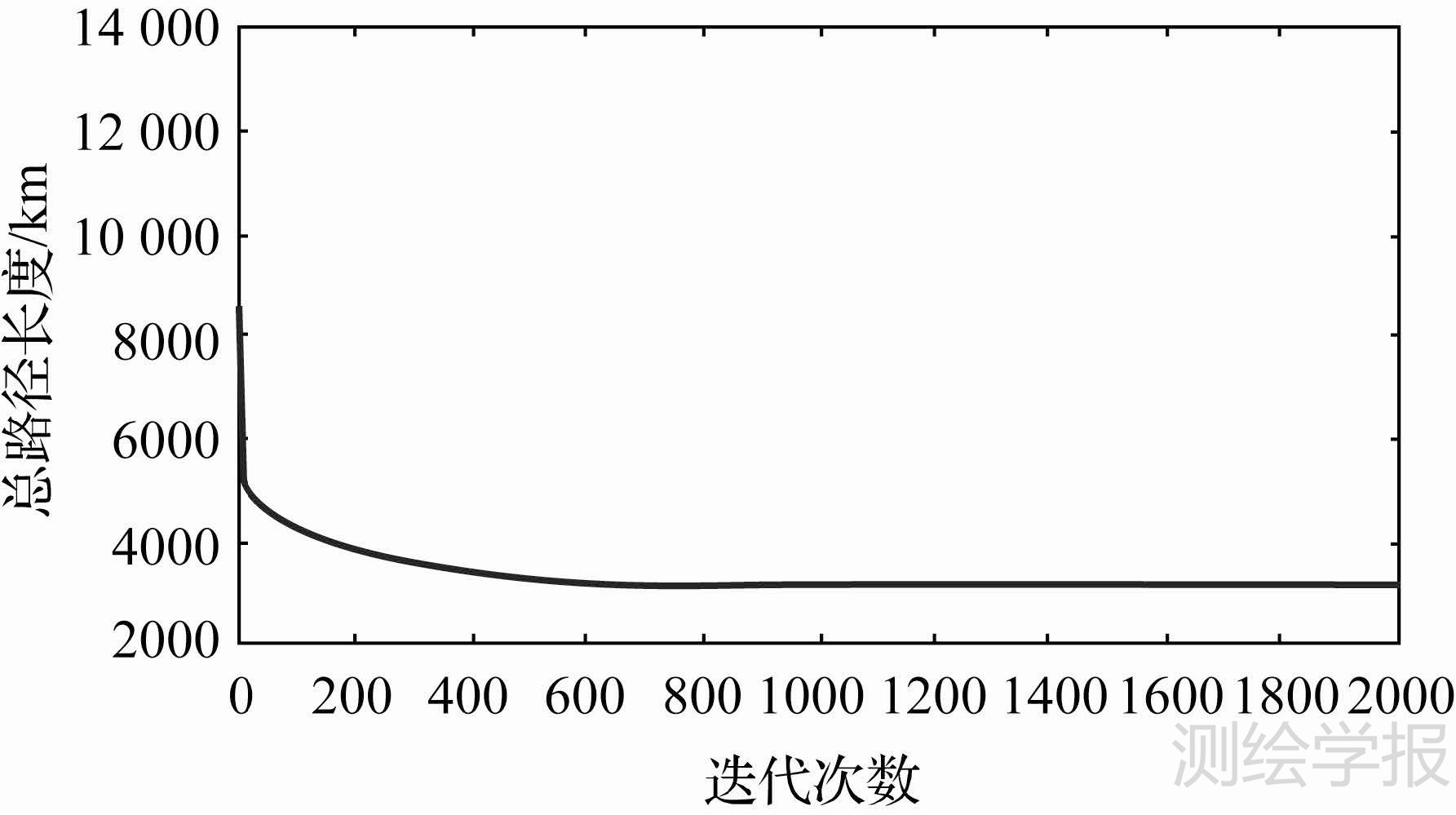
图 4以多仓库物流配送实例SZ6为例,给出了其总路径长度的迭代曲线。虽然初始解的总路径长度较大,本文的优化算法仍然能够较快地收敛到一个高质量的解。
|
| 图 4 总路径长度迭代曲线(SZ6) Fig. 4 The iterated curve of total routes length |
图5给出了SZ2和SZ6物流配送路线方案。由图图 5(a)可知,不同仓库服务区域的节点基本上位于对应的网络Voronoi区域内。在图 5(b)中,本文方法顾及货物储量的不足,进行区域边界调整,服务范围相应减小。在服务区域边缘,不同仓库出发的车辆配送路径相互重叠或交叉,进行协作,减少了总路径长度。因此,基于网络Voronoi图的空间启发式策略引导多个仓库在动态服务区域相互配合,协同完成物流配送任务。
综上所述,基于网络Voronoi图的启发式优化方法能够在15min内提供6400个客户点的大规模多仓库物流配送方案。
|
| 图 5 多仓库物流配送方案示例 Fig. 5 An example of multi-depot logistic distribution |
为了分析动态区域的效果,本文设计4种策略,分别是:无动态区域(S1,α=0),即是刚性的网络Voronoi划分,仓库之间无路径协作;窄动态区域(S2,α=200);一般动态区域(S3, α=500);宽动态区域(S4,α=1000)。以SZ6为例,进行多仓库物流配送优化,记录优化方案的路径长度和计算时间。
计算结果如 表 3所示。由表可知,4种策略的路径数量均相同。在路径长度上,无动态区域策略S1劣于动态区域策略(S2、S3、S4)。动态区域大小对优化方案也有影响。与策略S2和S4相比, S3的路径总长度为3157.755km,质量最好。试验结果表明:恰当的动态区域策略能够协调多个仓库之间的竞争与合作关系,进一步提高解的质量。在计算效率上,随着动态区域的扩大,计算时间有所增长,但增长幅度不大。
| 动态区域 | 路径数量R | 路径总长度L/km | 计算时间T/s |
| S1(α=0) | 81 | 3357.294 | 308.6 |
| S2(α=200) | 81 | 3247.427 | 311.9 |
| S3(α=500) | 81 | 3157.755 | 322.3 |
| S4(α=1000) | 81 | 3340.682 | 340.3 |
为了验证算法性能,将本文算法计算结果和其他算法进行比较。比较指标为路径数量、路径长度和计算时间。考虑到算法的可获得性,比较算法为ArcGIS10中的Network Analyst模块。利用该模块计算4.1节中多仓库物流配送实例。试验时ArcGIS10运行于和本文算法相同的计算平台。对于SZ5—SZ8,根据仓库货物储量的差异,需要人工预先设计各仓库的车辆配置方案。
试验结果如表 4所示。由表可知,本文算法的解显著优于ArcGIS的解。在解的质量上,ArcGIS的解的车辆数量为812条,略高于本文算法。然而,在路径长度指标上,ArcGIS解的路径长度和最少高于本文算法约9.1%(SZ3),最多高于本文算法约11.4%(SZ7),平均高于本文算法约10.8%。因此,ArcGIS的计算结果显著劣于本文算法。在计算时间上,ArcGIS的计算时间约为本文算法的4.72倍(2204.3/466.7)。本文算法的配送方案质量优于ArcGIS10,计算时间更少,算法性能显著优于ArcGIS。
| 问题实例 | 本文算法 | ArcGIS | ||||||
| 路径数量 R1 | 路径长度 L1/km | 计算时间 T1 | 路径数量 R2 | 路径长度 L2/km | 相对偏差 gap/(%) | 计算时间 T2/s | ||
| SZ1 | 40 | 2083.728 | 118.7 | 40 | 2328.803 | 11.8 | 960.0 | |
| SZ2 | 81 | 3150.316 | 310.8 | 81 | 3491.067 | 10.8 | 1780.8 | |
| SZ3 | 121 | 4051.624 | 562.2 | 121 | 4421.516 | 9.1 | 2489.2 | |
| SZ4 | 162 | 4749.621 | 850.5 | 162 | 5279.966 | 11.2 | 3420.5 | |
| SZ5 | 40 | 2114.839 | 125.3 | 40 | 2342.878 | 10.8 | 1005.6 | |
| SZ6 | 81 | 3157.755 | 322.3 | 82 | 3513.382 | 11.3 | 1840.0 | |
| SZ7 | 122 | 4066.205 | 576.3 | 122 | 4529.999 | 11.4 | 2618.4 | |
| SZ8 | 163 | 4850.447 | 867.8 | 164 | 5321.853 | 9.7 | 3520.0 | |
| 总路径数量 | 810 | 812 | ||||||
| 平均偏差 | 10.8 | |||||||
| 平均计算时间 | 466.7 | 2204.3 | ||||||
| 注: 相对偏差gap= (L2-L1)/L1×100% | ||||||||
由于存在多约束和多优化目标,大规模多仓库物流配送优化十分困难。本文提出了基于网络Voronoi图的大规模多仓库物流配送路径优化新方法。该方法利用仓库的网络Voronoi图对服务区域进行初始划分,顾及仓库容量差异修正区域边界,并调整边界邻近区域的仓库-客户服务关系,将局部搜索限定在网络K近邻内,充分利用有限的计算能力,在短时间内提供高质量的物流配送方案。利用深圳市的大规模多仓库物流配送优化实例进行验证,结果表明:该算法解的质量优于ArcGIS 10约为10.8%,计算时间约为其21.2%。本文方法可广泛用于电子商务、快递配送和城市垃圾收集中的方案设计,提高物流效率,减少物流费用。后续研究可以考虑仓库的重要程度,利用带权网络Voronoi图进行物流配送优化;顾及客户点的时间要求,优化附带时间窗的多仓库物流配送问题。同时,本文的空间启发式优化思想可以进一步拓展至其他空间相关优化问题,利用空间特性、空间结构和空间规律等,发展高效率的优化机制,应用于设施选址、应急疏散、资源调度等。
| [1] | QI Minyao.Research on the Logistics Oriented Spatial Information Service and Its Key Technical Issues [D]. Beijing:Institute of Remote Sensing Applications, Chinese Academy of Sciences,2006. (戚铭尧.面向物流的空间信息服务及其关键技术研究[D]. 北京:中科院遥感应用研究所, 2006.) |
| [2] | REPOUSSISP P, PARAKEVOPOULOS D, ZOBOLAS G, et al. A Web-based Decision Support System for Waste Lube Oils Collection and Recycling[J]. European Journal of Operational Research,2009, 195(3): 676-700. |
| [3] | SANTOS L, COUTINHO-RODRIGUES J, ANTUNES C H. A Web Spatial Decision Support System for Vehicle Routing Using Google Maps [J]. Decision Support Systems,2011, 51(1): 1-9. |
| [4] | SANTOS L, COUTINHO R J, CURRENT J R. Implementing a Multi-vehicle Multi-route Spatial Decision Support System for Efficient Trash Collection in Portugal [J]. Transportation Research Part A: Policy and Practice,2008, 42(6): 922-934. |
| [5] | LAPORTE G. Fifty Years of Vehicle Routing [J]. Transportation Science,2009, 43(4): 408-416. |
| [6] | LI Feiyue, GOLDEN B,WASIL E. Very Large-scale Vehicle Routing: New Test Problems, Algorithms, and Results [J]. Computers and Operations Research, 2005, 32(5): 1165-1179. |
| [7] | TOTH P,DANIELE V. The Vehicle Routing Problem [M]. Philadelphia:Society for Industrial and Applied Mathematics,2002. |
| [8] | ZACHARIADIS E E,KIRANOUDIS C T. A Strategy for Reducing the Computational Complexity of Local Search-based Methods for the Vehicle Routing Problem [J]. Computers and Operations Research, 2010, 37(12): 2089-2105. |
| [9] | HO W, HO G T S, JI P, et al. A Hybrid Genetic Algorithm for the Multi-depot Vehicle Routing Problem [J]. Engineering Applications of Artificial Intelligence,2008, 21(4): 548-557. |
| [10] | CORDEAU J F, GENDREAU M, LAPORTE G. A Tabu Search Heuristic for Periodic and Multi-depot Vehicle Routing Problems [J]. Networks, 1997, 30(2): 105-119. |
| [11] | KUO, Y, WANG C C. A Variable Neighborhood Search for the Multi-depot Vehicle Routing Problem with Loading Cost [J]. Expert Systems with Applications, 2012, 39, 6949-6954. |
| [12] | YU B, YANG Z Z, XIE J X. A Parallel Improved Ant Colony Optimization for Multi-depot Vehicle Routing Problem [J]. Journal of the Operational Research Society, 2010, 62, 183-188. |
| [13] | SHI Yarong, WAN Difang, LI Shuangyan, et al. Research of Vehicle Routing Problem Based on GIS[J].System Engineering-Theory and Practice, 2009, 29(10):76-85. (史亚容,万迪昉,李双燕,等.基于GIS的物流配送路线规划研究[J]. 系统工程理论与实践, 2009, 29(10):76-85.) |
| [14] | FANG Zhixiang, TU Wei, LI Qingquan, et al. A Voronoi Neighborhood-based Search Heuristic for Distance/Capacity Constrained Very Large Vehicle Routing Problems [J]. International Journal of Geographical Information Science, 2013, 27(4): 741-764. |
| [15] | TU Wei, LI Qingquan, FANG Zhixiang. A Heuristic Algorithm for Large Scale Vehicle Routing Problem [J]. Geomatics and Information Science of Wuhan University,2013, 38(3): 307-310. (涂伟,李清泉,方志祥. 一种大规模车辆路径问题的启发式算法[J]. 武汉大学学报:信息科学版, 2013, 38(3): 307-310.) |
| [16] | ZHAO Yuan, ZHANG Xinchang, KANG Tingjun. A Parallel Ant Colony Optimization Algorithm for Site Location [J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3):322-327. (赵元, 张新长, 康停军.并行蚁群算法及其在区位选址中的应用[J]. 测绘学报,2010, 39(3): 322-327.) |
| [17] | LIU Jiubao, TANG Xinming, LIU Zhengjun, et al. Research algorithm of Shelter Assignment Based on Capability Limitation and Optimization of the Travel Cost [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 489-494. (刘久保, 唐新明, 刘正军,等.基于行程距离最优及容量受限的避难所分配算法研究[J]. 测绘学报, 2011, 40(4), 489-494.) |
| [18] | OKABE A, SATOH T, FURUTA T, et al. Generalized Network Voronoi Diagrams: Concepts,Computational Methods,and Applications[J]. International Journal of Geographical Information Science, 2008, 22(9): 965-994. |
| [19] | XIE Shunping, FENG Xuezhi, WANG Jiechen, et al. Radiation Domain of Commercial Centers in Nanjing Based on Analysis of Road Network Weighted Voronoi Diagram [J]. Acta Geographica Sinica, 2009, 64(12): 1467-1476.(谢顺平, 冯学智, 王结臣,等. 基于网络加权Voronoi图分析的南京市商业中心辐射域研究[J]. 地理学报,2009,64(12): 1467-1476.) |
| [20] | XIE Shunping, FENG Xuezhi, DU Jinkang. Maximal Covering Spatial Optimization Based on Network Voronoi Diagrams Heuristic and Swarm Intelligence [J]. Acta Geodaetica et Cartographica Sinica,2011, 40(6): 778-883. (谢顺平, 冯学智, 都金康.基于网络Voronoi图启发式和群智能的最大覆盖空间优化[J]. 测绘学报,2011,40(6): 778-883.) |
| [21] | AI Tinghua, YU Wenhao. Algorithm for Constructing Network Voronoi Diagram Based on Flow Extension Ideas[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 760-766. (艾廷华,禹文豪. 水流扩展思想的网络空间Voronoi图生成[J]. 测绘学报,2013, 42(5): 760-766.) |
| [22] | ZHU Weining, MA Jinsong, HUANG Xinyuan, et al. A Study of GIS Spatial Competition Analysis Model Based on Projective Weighted Voronoi Diagrams[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 146-150. (朱渭宁, 马劲松, 黄杏元,等.基于投影加权Voronoi图的GIS空间竞争分析模型研究[J]. 测绘学报,2004, 33(2): 146-150.) |
| [23] | MOLE R,JAMESON S.A Sequential Route-building Algorithm Employing a Generalized Savings Criterion [J]. Operational Research Quarterly, 1976,27(2): 503-511. |
| [24] | XIE Shunping, FENG Xuezhi, LU Wei. Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 88-94. (谢顺平, 冯学智, 鲁伟.基于道路网络分析的Voronoi面域图构建算法[J]. 测绘学报,2010, 39(1): 88-94.) |