2.广东工贸职业技术学院,广东 广州 510510;
3. 广东省城市化与地理环境空间模拟重点实验室,广东 广州 510275
2. Guangdong College of Industry and Commerce, Guangzhou 510510,China;
3. Guangdong Key Laboratory for Urbanization and Geo-simulation, Guangzhou 510275,China
建筑物是城市三维建模的重要元素,而建筑物屋顶边界的提取则是三维建模中的关键步骤。随着机载激光雷达(light detection and ranging,LiDAR)点云分辨率的不断提高,利用LiDAR数据进行建筑物的边界提取,成为近年来的研究热点。国内外研究人员提出了大量的理论框架与算法,主要包括:形态学[1,2,3,4]、Alpha-shapes算法[5]、最小二乘模型法[6]、DP算法[7]及图像分割[8,9,10,11,12]等方法。
以上算法的数据源一部分是利用光谱影像和LiDAR点云集成[2,3,10,11,12],一部分则是单独使用LiDAR点云[4,5,6,7,8,9]。LiDAR点云具有高程和强度信息,光谱影像具有光谱信息,二者集成相互补充可以更好地提取建筑物边界,但集成数据的误差要比使用单一数据复杂[7]。对算法而言,形态学在处理不规则点云的建筑物边界提取时,得到的边界易断裂,较难达到满意的效果;Alpha-shapes及DP算法在处理不同形状的建筑物时,需手动调整模型参数,因而在处理同一幅图像时需要多次交互;最小二乘法则假定建筑物边界是相互垂直的,但实际建筑物形状是多样的;图像分割中的活动轮廓模型(active contour model,ACM) [13],将边界提取问题归结为最小化一个封闭曲线的能量泛函,使任意形状的目标边界提取变得更加智能[14, 15] 。
目前有代表性的ACM主要有经典Snake模型[13]、基于边缘特征的ACM (geodesic active contour model, GAC模型)[16]、基于区域特征的ACM(region-scalable fitting model,RSF模型)[17]以及基于全局特征的ACM(chan-vese model,C-V模型)[18]4大类,并广泛应用于医学影像的病变提取、视频图像的分割及轮廓提取等领域。4类模型各有特点:经典Snake模型的曲线为参数型曲线,模型演化时依赖于曲线的参数,能量函数的计算复杂[19];GAC模型是基于图像的梯度进行边界提取,对初始边界比较敏感,对弱边界处理比较困难,且分割时间较长[20];C-V模型可以处理无明显梯度和纹理的图像,亦可以提取图像的内部结构,但对背景不均匀的目标边界提取较困难,且由于只考虑全局灰度信息,容易出现过分割导致一些地物提取失败;RSF模型采用局部区域信息进行边界提取,解决了C-V模型的上述问题[15];4类模型仅用于处理单一波段的图像;为解决多波段图像的边界提取,文献[21]提出了集成活动轮廓(integrated active contour,IAC)模型,该模型为GAC模型与C-V模型矢量形式的结合。
对LiDAR点云来说,可根据分类后的屋顶面点云来确定建筑物的屋顶边界[22]。但在利用离散点云进行建筑物边界提取时,点云不规则分布所产生的无数据区域,导致建筑物内部 “灰度不均匀”,因而单一采用图像的边缘和全局信息,会使图像内部的无值区域被提取为边界,从而导致提取失败。为解决该问题,本文将利用RSF模型的区域信息来解决离散点云数据内部的灰度不均匀,利用GAC模型的边缘信息控制曲线停靠在建筑物的外边界,即将两模型进行集成,并推广至多波段图像得到一种新的ACM模型,进而利用该模型对栅格化的建筑物点云进行处理得到其边界。
2 原理与算法 2.1 本文模型模型能量函数的定义:I: Ω→R是一幅输入图像;m为图像的维数;C是一闭合曲线。能量函数定义如下
式中,第一项为边缘分量,第二、三项为区域分量;参数μ和λ(i)1 、λ(i)2 是边缘信息和区域信息的权重,均为正常数;m为图像的维数;gcolor为彩色图像的边缘函数; Ω1、Ω2分别为演化曲线C的内部与外部;f(i)1 、f(i)2 为曲线C在图像第i维内外部的灰度拟合值;σ表示尺度参数,控制中心点x邻域的大小,当邻域点y离中心点x越远时,点y处的均方误差对局部拟合能量的影响越大,反之越小并趋于0;Kσ是一高斯核函数,通常取Kσ(u)=12πσe-u2/2σ2,σ>0。该模型可直接处理离散LiDAR点云生成的栅格数据,无须对点云进行内插,减少了数据预处理环节的误差。
2.2 数值实现本文利用变分水平集方法对式(1)的能量函数进行求解。曲线C采用水平集的表达方式:曲线CΩ是Lipschitz函数øΩ→R的零水平集表示,ø为水平集函数。采用文献[19]建议的初始化方案,初始曲线C的内部为负,外部为正。引入Heaviside函数的正则化形式H(ø),并添加水平集规则项,式(1)可以表达为
式中
式中,v为一正常数;R(x,y)为当前点(x,y)的邻域点;σ控制邻域大小;K>0为反差系数;ε为一正常数。
利用梯度下降法最小化能量函数式(2),得到梯度下降流如下
式中,δ(ø)为正则化Heaviside函数的导数,其形式为
式中,Δø为水平集函数ø的4邻点差分。 2.3 LiDAR点云栅格化方法
本文的点云栅格化是将分类后的点云按照高程值直接转换为灰度值,并将激光点定义到栅格单元中,无需内插。
理想情况下,一个栅格包含一个激光点,因而栅格的边长L可考虑由区域面积S和该区域分类前的激光总点数N来大致确定,如式(4)所示
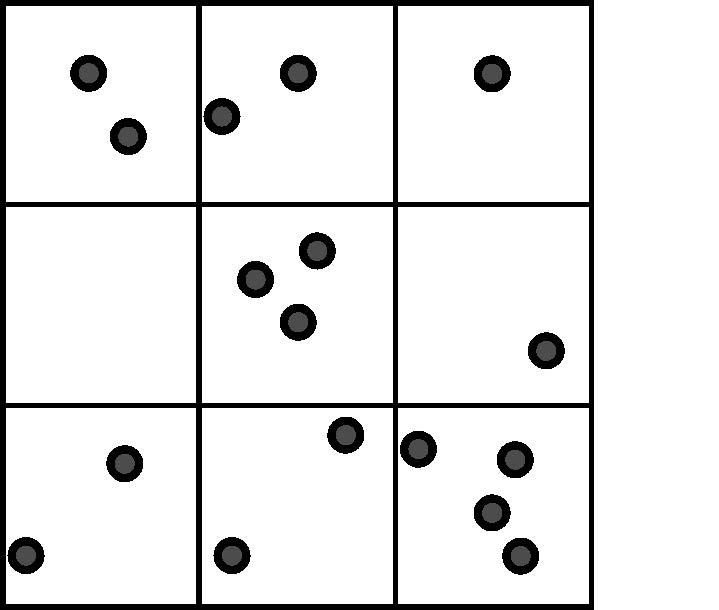
由于LiDAR点云的空间分布不均匀,根据式(4)确定的格网会出现的激光点个数为0,1和大于1三种情况,如图 1所示。
对于激光点数大于1的情形,其栅格高程值按照最近距离法处理
式中,xpi、ypi代表栅格内第i个激光点的坐标;xo、yo代表栅格中心的坐标;当两点间距离d最小时,将该点i的高程赋给栅格,若距离相等,则取两点的高程均值作为本栅格高程。
|
| 图 1 激光点在栅格中的分布 Fig. 1 Distribution of LiDAR points in the grid |
鉴于本文模型的特点,对于激光点个数为0的情况,将不作处理;而激光点个数为1时,则直接将激光点高程值赋给栅格。如此得到的栅格影像将存在大量的无值区域。为了更好地突出栅格影像的高程差异,本文将上述处理得到的影像按照高程值分层设色作为模型的输入影像。
2.4 基于本文模型的建筑物屋顶边界提取算法最小化本文模型的能量函数就可以获得建筑物的边界,算法流程如下:
Input:输入分类后的建筑物点云栅格影像I,最大迭代次数N及初始水平集函数ø0。
Output:水平集函数ø,即为建筑物边界。
(1) 初始化水平集函数øi=ø0;
(2) 对于每一次迭代i,执行如下计算;
(3) 对每一点x,利用式(3)计算f(i)1 、f(i)2 ,进而计算e1、e2;
(4) 利用式(3)计算梯度下降流 ;
;
(5) 显式方案计算水平集函数øi+1=øi+
Δt· ,Δt为时间步长;
,Δt为时间步长;
(6) 若øi+1= =øi,跳出循环;
(7) 结束。
3 试验分析 3.1 试验环境及试验数据试验采用单PC环境,内存配置为4GB,CPU为Intel Core i5-2400,主频为3.10GHz。操作系统环境为64位Windows 7 SP1,算法以Matlab7.6为平台。
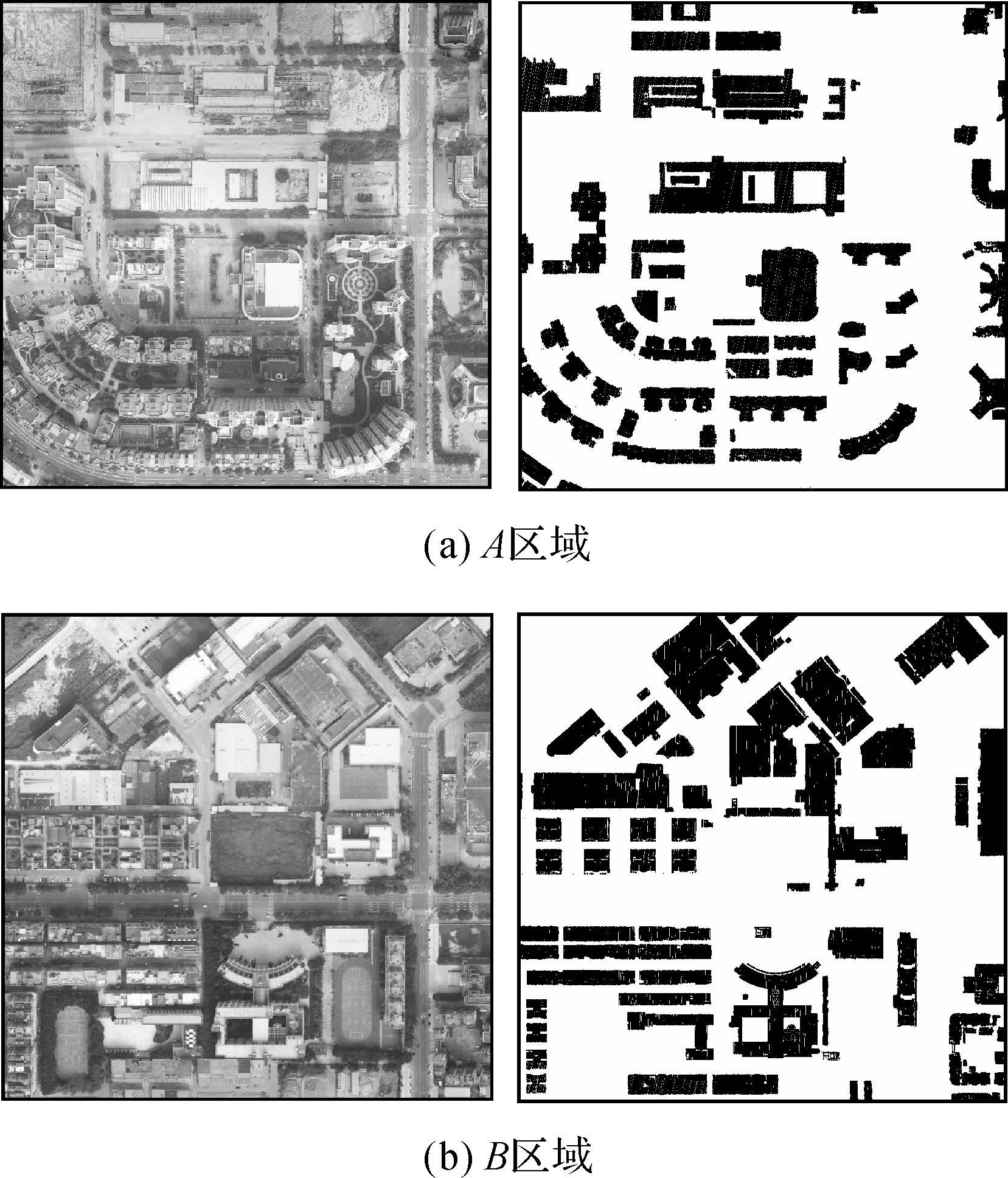
试验数据由广州建通测绘公司提供,测区均位于东莞市城区,包括LiDAR点云数据以及随机影像数据。数据采集仪器为天宝HARRIER56,相对行高1000m左右。试验区域A、B面积皆为500m×500m,点云的平均密度为2.5点/m2。试验区域地物类型主要为建筑物,形状各式各样,同时也包括一些高低不等的植被。原始的点云数据通过Microstation V8数据处理软件分类为地面,屋顶、墙面和植被及其他非地面点;为保证分类质量,对软件分类的结果进行检查并修正分类错误。本文采用分类后的屋顶点云,如图 2,A区域屋顶点云总数为302805个,B区域总点数为463315个。所选数据的漏点区域面积较小 (漏点形成的原因主要是在数据采集时,遇到镜面反射或者高吸收率的地物材料等,造成LiDAR无法接收回波信息;或是一些低矮房屋被树木遮挡,造成LiDAR激光无法穿透树木到达屋顶)。
|
| 图 2 试验区域影像及屋顶点云 Fig. 2 The DOM and building roof LiDAR point cloud of experiment |
将A、B两区域分类后的屋顶点云转换为栅格形式,两区域栅格大小均为1112×1112,按照高程分层设色,如图 3所示,由于点云的离散分布使转换后的栅格数据存在无值区域。

|
| 图 3 屋顶点云栅格数据 Fig. 3 The LiDAR point cloud of building roof in the raster format |
本文借助清华山维EPS软件,基于正射影像进行建筑物边界的手动提取,提取过程中EPS可以自动进行建筑物的投影差改正,因而得到的结果可以直接作为参考数据,如图 4所示。

|
| 图 4 试验区屋顶边界参考数据 Fig. 4 The reference data of the building roof boundary |
为验证本文模型的有效性,试验选择了IAC模型和彩色图像的GAC模型(GACcolor)[19]与本文模型分别对图 3(a)和图 3(b)的栅格数据进行处理。参数ν控制水平集规则项作用的相对大小,一般满足Δtν≤0.25;参数σ表示中心点邻域大小的尺度参数,取值越大运算速度越慢;cg为GACcolor模型的速度常数。经反复调试,模型的参数设置如表 1 所示。
3.3 试验结果栅格屋顶点云数据既无明显的边缘,也缺乏明显的纹理,且建筑物内部存在无值区域。根据IAC模型的特征,可将建筑物作为对象,无值区域作为背景,模型能量函数达到最小值的状态时,曲线演化到对象和背景的分界处,而建筑物内部的无值区域为背景,故被当做边界提取出来,如图 5(b)和图 5(c)所示,出现了过分割的现象,提取几乎失败。
| 方法 | 参数 | |||||||||
| μ | ε | λ(i)1 | λ(i)2 | v | m | σ | cg | K | Δt | |
| IAC模型 | 0.01 | 1.0 | 0.005 | 0.005 | — | 3 | — | — | 5 | 2.0 |
| GACcolor模型 | — | 1.0 | — | — | 0.01 | 3 | — | 0.65 | 5 | 0.1 |
| 本文模型 | 0.002×2552 | 1.0 | 1 | 1 | 0.08 | 3 | 5 | — | 5 | 2.0 |
GACcolor模型为基于边缘的ACM,曲线在梯度变化最大的位置停止运动;栅格屋顶点云数据中建筑物内部有无值区域,即存在梯度。在初始边界设置正确的情况下,两区域的建筑物边界提取结果如图 5(e)和 5(f)所示,图中大多数建筑物的外边界被提取出来;由于设置了速度常数cg,建筑物内部梯度变化较大的区域被提取出来,如图 5(e)和5(f)中三角形所标之处;但速度常数cg的取值并不能适合所有的建筑物,因而图中多处邻近建筑物出现了胶合,如图 5(e)和5(f)中四角形星所标之处。

|
| 图 5 初始曲线设定及建筑物边界提取结果 Fig. 5 The initial contour and building extraction results |
本文模型可以解决背景灰度不均匀的对象提取问题,试验的栅格屋顶点云数据可以将建筑物对象的灰度看做不均匀,而背景灰度均匀。模型的第2、第3分量为局部区域信息拟合项,可以解决上述不均匀问题,能较好地克服图像中无值区域对建筑物边界的影响,准确地将线段端点连接起来,形成连续的建筑物轮廓,如图 5(h)和5(i)的提取结果。但对于漏点面积较大的无值区域,本模型会将其提取为内部边界,如图 5(h)和5(i)五角星所标之处。整体来讲,图 5的3个模型提取结果中,本文模型的提取精度较高。
另外,初始边界的设置对于GACcolor模型来说要求较高,若设置不正确则会影响最终的提取结果;但对于另外两模型而言,只会影响其运算时间,对最终结果影响不大。另外,本文模型引入了水平集规则项,这既控制了水平集函数为距离符号函数,又大大降低了重新初始化水平集函数的计算,虽然要作多次卷积,但最终的运算时间也比另外两个模型少,具有较好的实时性。
4 精度分析本文简化了文献[23]的评价策略,定量地评估本文模型的提取精度。该评价策略利用匹配度、形状相似度以及位置精度3个因子来分析提取精度。
(1)匹配度因子
匹配度采用了传统图像分类的评估参数,本文选择质量因子(quality,简称Q)作为评价指标
式中,TP为同属于提取结果和参考数据的区域;FP为属于提取结果但不属于参考数据的区域;FN为属于参考数据但不属于提取数据的区域。
(2)形状相似度因子
影响形状的因素主要是面积差(area difference,简称rarea)和周长差(perimeter difference,简称rperi)。
式中,Ae表示提取数据的面积;Ar表示参考数据的面积;Pe表示提取数据的周长;Pr表示参考数据的周长。(3)位置精度因子
位置精度因子中,本文选用建筑物中心的距离差(简称dctr)进行评价
式中,Xe、Ye表示提取建筑物中心的坐标;Xr、Yr表示参考建筑物中心的坐标。利用上述评价标准,分别对GACcolor模型与本文模型提取的两组数据进行评估,结果如表 2所示。
| 提取精度 | GACcolor模型 | 本文模型 | ||||||||
| 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | |||
| A区域 | Q | 0.502 | 1 | 0.797 | 0.203 | 0.561 | 1 | 0.881 | 0.121 | |
| rarea | 0.012 | 3.945 | 0.606 | 0.557 | 0.001 | 3.022 | 0.455 | 0.383 | ||
| rperi | 0.009 | 3.112 | 0.507 | 0.488 | 0.001 | 2.030 | 0.144 | 0.290 | ||
| dctr | 0.025m | 11.763m | 1.022m | 0.769 | 0.048m | 5.920m | 0.614m | 0.582 | ||
| B区域 | Q | 0.301 | 0.996 | 0.552 | 0.463 | 0.547 | 0.998 | 0.828 | 0.130 | |
| rarea | 0.011 | 12.766 | 0.913 | 0.501 | 0.050 | 2.986 | 0.545 | 0.420 | ||
| rperi | 0.001 | 3.045 | 0.328 | 0.166 | 0.008 | 2.531 | 0.156 | 0.100 | ||
| dctr | 0.501m | 10.008m | 1.179m | 0.773 | 0.032m | 7.580m | 0.780m | 0.602 | ||
由表 2中A、B两区域的建筑物提取精度对比可见,本文模型可以得到较高的匹配度、形状相似度及位置精度。在两个区域的数据提取结果中,本文模型匹配度质量因子Q的均值皆高于GACcolor模型;形状相似度中,由于GAC模型cg常数的影响,多栋建筑物胶合在一起,因而面积差及周长差均比本文模型大、精度较差;另外本文模型的提取结果中,建筑物中心点位置位差均值皆小于1m。以上各因子的结果均表明本文模型在利用屋顶栅格点云提取边界时可以达到较好的效果。
5 结 论本文研究的重点在于对分类后的屋顶点云进行处理,得到建筑物的边界。研究中,通过对基于边缘和局部信息的ACM进行集成,得到了一种多波段图像边界提取的方法。该方法可以直接对分类后点云转换的栅格数据进行处理,无须内插;可以解决点云分布不规则对内外边界的影响;相对于其他ACM,本文模型对初始曲线的设置不敏感。另外模型计算时添加了水平集规则项,大大降低了重新初始化水平集函数的时间,具有较好的实时性。在对东莞市两个区域的数据试验中,定性和定量的评价结果皆显示,本文模型处理结果均优于IAC模型和GACcolor模型,是一种较稳健的边界提取模型。不过,点云分类精度直接影响着建筑物屋顶边界的提取精度,文中的分类是基于软件的半自动分类,其分类误差需要人工判断并修改,因而提高点云分类的精度及自动化程度是下一步的研究方向。
| [1] | MENG X, WANG L, CURRIT N. Morphology-based Building Detection from Airborne LiDAR Data[J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(4): 437-442. |
| [2] | AWRANGJEB M, RAVANBAKHSH M, FRASER C S. Automatic Detection of Residential Buildings Using LiDAR Data and Multispectral Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(5): 457-467. |
| [3] | EKHTARI N, ZOEJ M J V, SAHEBI M R, et al. Automatic Building Extraction from LiDAR Digital Elevation Models and WorldView Imagery[J]. Journal of Applied Remote Sensing, 2009, 3(1): 033571-033571-12. |
| [4] | MILIARESIS G, KOKKAS N. Segmentation and Object-based Classification for the Extraction of the Building Class from LiDAR DEMs[J]. Computers & Geosciences, 2007, 33(8): 1076-1087. |
| [5] | SHEN W, ZHANG J, YUAN F. A New Algorithm of Building Boundary Extraction Based on LiDAR Data[C]//Proceedings of the 19th International Conference on Geoinformatics. Shanghai:[s.n.],2011: 1-4. |
| [6] | SAMPATH A, SHAN J. Urban Modeling Based on Segmentation and Regularization of Airborne Lidar Point Clouds[C]//Proceedings of the 20th International Society for Photogrammetry and Remote Sensing Congress. Istanbul:[s.n.],2004: 937-942. |
| [7] | LIU C, SHI B, YANG X, et al. Automatic Buildings Extraction from LiDAR Data in Urban Area by Neural Oscillator Network of Visual Cortex[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013,6(4): 2008-2019. |
| [8] | SAMPATLT A, SHAN J. Building Boundary Tracing and Regularization from Airborne LiDAR Point Clouds[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(7): 805-812. |
| [9] | ZHANG K, YAN J, CHEN S C. Automatic Construction of Building Footprints from Airborne LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2523-2533. |
| [10] | KABOLIZADE M, EBADI H, AHMADI S. An Improved Snake Model for Automatic Extraction of Buildings from Urban Aerial Images and LiDAR Data[J]. Computers, Environment and Urban Systems, 2010, 34(5): 435-441. |
| [11] | SUN Ying, ZHANG Xinchang, KANG Tingjun, et al. Improved GAC Model for Automatic Building Extraction from LiDAR Point Clouds and Aerial Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3):337-343.(孙颖, 张新长, 康停军, 等. 改进GAC 模型在点云和影像自动提取建筑物边界中的应用[J]. 测绘学报, 2013, 42(3): 337-343) |
| [12] | KABOLIZADE M, EBADI H, AHMADI S. An Improved Snake Model for Automatic Extraction of Buildings from Urban Aerial Images and LiDAR Data[J]. Computers, Environment and Urban Systems, 2010, 34(5): 435-441. |
| [13] | KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active Contour Models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331. |
| [14] | SAKALLI M, LAM K M, YAN H. A Faster Converging Snake Algorithm to Locate Object Boundaries[J]. IEEE Transactions on Image Processing, 2006, 15(5): 1182-1191. |
| [15] | JING Y, AN J, LIU Z. A Novel Edge Detection Algorithm Based on Global Minimization Active Contour Model for Oil Slick Infrared Aerial Image[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2005-2013. |
| [16] | CASELLES V,MOREL J M,SAPIRO G. Geodesic Active Contours[J]. Computer Vision and Image Understanding,1997 (22):61-79. |
| [17] | LI C, KAO C Y, GORE J C, et al. Minimization of Region-Scalable Fitting Energy for Image Segmentation[J]. IEEE Transactions on Image Processing, 2008, 17(10): 1940-1949. |
| [18] | CHAN T F, VESE L A. Active Contours without Edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277. |
| [19] | WANG Dakai,HOU Yuqing,PENG Jinye. Image Processing on Partial Differential Equations [M]. Beijing: Science Press,2008:88-96.(王大凯,侯榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社,2008:88-96.) |
| [20] | HE L, PENG Z, EVERDING B, et al. A Comparative Study of Deformable Contour Methods on Medical Image Segmentation[J]. Image and Vision Computing, 2008, 26(2): 141-163. |
| [21] | SAGIV C, SOCHEN N A, ZEEVI Y Y. Integrated Active Contours for Texture Segmentation[J]. IEEE Transactions on Image Processing, 2006, 15(6): 1633-1646. |
| [22] | WEI Zheng,YANG Bisheng,LI Qingquan. Automated Extraction of Building Footprints from Mobile LiDAR Point Clouds[J]. Journal of Remote Sensing, 2012,16(2):286-296.(魏征, 杨必胜, 李清泉. 车载激光扫描点云中建筑物边界的快速提取[J]. 遥感学报, 2012,16(2):286-296. ) |
| [23] | ZENG C, WANG J, LEHRBASS B. An Evaluation System for Building Footprint Extraction from Remotely Sensed Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1640-1652. |