2. 中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，江苏 徐州221116
2. Key Laboratory for Land Environment and Disaster Monitoring of SBSM,China University of Mining and Technology,Xuzhou 221116,China
1 引 言
全球定位系统(global positioning system，GPS)和惯性导航系统(inertial navigation system，INS)是世界上应用较为广泛的两种导航技术，将二者结合起来，可以扬长补短发挥各自的优势。然而实际导航中由于卫星信号遮挡、多路径效应、观测粗差等因素影响观测信息质量和动力学方程存在的不确定性，常导致滤波结果出现较大误差[1 ,2]。近年来，很多学者基于残差分量和自适应滤波做了大量研究[3, 4, 5, 6]，文献[7]基于量测向量中的粗差对状态向量滤波值的影响规律导出了抗差卡尔曼滤波模型；文献[8]提出了一种基于移动窗口的函数模型和随机模型系统误差自适应拟合法；文献[9]提出基于等效残差积探测粗差的方差-协方差分量估计算法。但当GPS/INS动态导航过程中观测信息无冗余时，残差分量包涵观测信息的误差和动力学模型误差的双重影响，难以准确采用抗差或自适应算法[10, 11, 12]。
随着以神经网络(neural network，NN)和支持向量回归(support vector regression,SVR)为代表的人工智能算法不断发展，机器学习为解决复杂非线性问题提供了新思路。文献[13]利用一个多层神经网络训练载体运动状态与相应卡尔曼滤波状态之间的映射关系进而建立相似性阈值判断方法；文献[14]采用神经网络与小波分析混合算法；文献[15]采用径向基神经网络方法；文献[16]结合模糊逻辑与神经网络算法；文献[17]基于神经网络预测坐标重构滤波器参数；文献[18]采用改进神经网络对滤波器状态在线预报修正，给出组合导航自适应算法；而神经网络仍存在局部最优解、拓扑结构确定以及“维数灾难”等难以解决的问题。文献[19]将最小二乘支持向量机引入组合系统故障导航模型，得出最小二乘支持向量机优于神经网络算法；但构建支持向量回归模型时，凭经验选取训练参数将影响回归精度和其泛化能力。
针对上述问题，本文基于遗传算法(genetic algorithm，GA)在全局范围内选取SVR训练模型的最优参数，给出改进的SVR辅助GPS/INS组合导航抗差自适应滤波算法。
2 GPS/INS组合导航抗差自适应滤波根据捷联惯性导航误差方程，选取24维系统状态参数X=[XNarXInsXAntXGrav]T
式中，δpN、δpE、δpU为位置误差;δvN、δvE、δvU为速度误差；φN、φE、φU为姿态误差；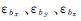
为陀螺漂移偏差；
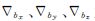为加速度计偏差；
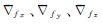为加速度计尺度因子偏差；δIx、δIy、δIz为杆臂误差；δgN、δgE、δgU为重力误差；xNav、xIns、xAnt和xGrav分别为导航误差向量、传感器测量误差矢量、杆臂误差矢量和重力误差矢量。下标b表示传感器偏差，f表示尺度因子。
GPS/INS组合导航系统状态方程离散化后得[20]
式中，Xk和Xk－1分别为时刻k和k-1时刻状态向量；Φk,k－1为离散化后的状态转移矩阵；wk为动力学模型误差向量。
取GPS和INS在输出的纬度、经度和高程坐标差构造观测方程
式中，Zk为观测向量；Hk为观测矩阵；rk为观测噪声向量，且wk、rk满足式(4) 式中，δkj为Kronecker-δ函数；Qk为动力学模型误差的非负定方差矩阵；Rk为观测噪声的对称正定方差矩阵。则离散系统抗差自适应卡尔曼滤波基本方程如式(5)、式(6)求解
预测过程
更新过程
式中，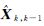
为一步预测状态向量；Σk,k－1为一步预测状态协方差矩阵；
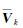为新息向量；Kk为增益矩阵；
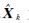为估计状态向量；Σk为估计状态协方差矩阵；αk为自适应因子；γk为抗差因子。
2.1 自适应因子
式(5)中常用的自适应因子估计算法有Sage开窗估计[21]，递推估计法[2]等。为反映当前历元模型异常大小，本文采用单历元残差估计法，此时自适应因子αk表达式为[22]
式中，
为估计状态与一步预测状态差。
抗差估计算法有“丹麦法”、IGG三段法、IGGⅢ双因子等价权等[2]，本文采用观测向量预测残差迭代求抗差因子，式(6)中抗差因子γk类似IGGⅢ函数表达式[23]
式中，k0、k1为阈值参数，通常k0取2.5～3.5，
分别为观测向量预测残差及其权倒数；σk=1.4826×Med
为由中位数计算的方差因子。
自适应因子和抗差因子发挥着调节动力学模型信息和观测信息对滤波结果贡献大小的作用。自适应因子和抗差因子需每次更新后进行迭代计算，为保证导航的实时性，根据计算机性能设置最大迭代次数和相邻两次预测状态限差。
3 GA-SVR辅助异常检测算法由于GPS/INS组合中观测值无冗余，基于残差向量检测出异常时，残差向量受观测异常和动力学模型异常的双重影响导致很难判定异常来源，设计一种基于GA-SVR算法预测观测值辅助的异常检测算法，算法流程如图 1所示。具体步骤如下：
|
| 图 1 GA-SVR辅助异常检测算法 Fig. 1 GA-SVR aided anomaly detection |
(1) 在GPS/INS滤波器中进行“整体异常检测”，如果未检测到异常直接输出导航解，同时将速度、姿态、加速度增量、姿态增量和坐标差作为输入和输出构建GA-SVR映射模型。
(2) 如果检测到异常，则认为观测异常或动力学异常至少存在一项。基于输入和GA-SVR模型预测出“次优观测值”。
(3) 将“次优观测值”代替“原观测值”，再一次在滤波器中进行“整体异常检测”。
(4)此时，如果未检测到异常，则认为“原观测值”存在异常，采用基于“次优观测值”的抗差估计滤波算法解算导航解。如果检测到仍然存在异常，则认为动力学模型存在异常(这时存在两种可能：①仅动力学模型存在异常；②动力学模型和原观测值都存在异常)，采用基于次优观测值的自适应滤波算法解算导航解。
3.1 滤波异常整体检验由于动态导航滤波结果往往含有观测异常和动力学模型异常的共同影响，采用观测残差和预测状态向量残差的二次型进行滤波整体异常检测，整体误差检验用于检测观测模型和动力学模型的整体误差量级，如式(7)所示[2]
式中，Vk为观测向量预测残差；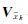
状态向量预测残差；Pk为观测值权阵；
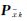预测状态权阵。各变量如下所示
基于观测噪声向量rk和动力学模型误差向量wk满足高斯白噪声条件时，整体检测统计量服从卡方分布，可化为式(8)
式中，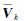
如式(6)所示；
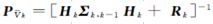；nk为多余观测数；χα2(nk)为预警率α下的阈值。
此时，故障检测的判定标准如式(9)所示，满足式(9)判定滤波结果无异常，否则存在异常
3.2 GA-SVR训练回归模型
由于当前速度、姿态、加速度和姿态增量与对应位置增量存在非线性映射关系[19]。若能预测出较精确的位置增量便可计算次优预测观测值，根据此次优观测值可以辅助异常判断，解算出稳定可靠的导航解。为了预测次优观测值，本文基于GA算法确定最优参数，训练出SVR回归模型。以相邻两个历元ti、ti+1 之间的速度vt、姿态φt，加速度增量
、姿态增量
为训练输入，GPS位置增量ΔPti=Pti+1－Pti训练输出，GA-SVR回归模型构建如图 2所示。
|
| 图 2 基于GA改进SVR算法 Fig. 2 Improving SVR algorithm Based on GA |
支持向量机是建立在VC维理论和结构风险最小化原则基础上的新型机器学习方法。其基本思想是通过用内积函数定义的非线性变换将输入空间映射到一个高维的特征空间，在高维的特征空间中寻找输入变量和输出变量之间的映射模型[24, 25]。
假设xi为速度、姿态、加速度增量、姿态增量，yi为坐标差，则GA-SVR映射模型训练数据集为 (xi，yi) i=1，2，…，l,xi∈Rn,yi∈R 式中，xi是第i个输入向量；yi是第i个标量输出；l是样本数。支持向量回归的基本思想是利用满足Mercer条件的核函数将输入数据x映射到高维特征空间，并在该空间构造优化超平面
进行回归计算。式中，ω为权重向量；φ(x)为映射函数；b为偏置项。为求优化超平面，引入不敏感损失函数ε和惩罚参数C，根据Wolfe对偶理论，将参数ω、b的求解问题转变为最优化问题，如式(11)所示 式中，αi*、αi、αj*、αj为非负拉格朗日乘子。
式(11)属于凸二次规划问题，其可行域为空，因此一定有解。设优化问题的最优解为
，则
鉴于径向基函数在处理空间线性不可分数据时具有较好的效果，引入径向基核函数式(12)，将其作为式(10)中φ(x)的映射函数
则超平面回归函数为
径向基核函数中控制半径的参数γ和惩罚参数C的选取是否合理直接决定最优超平面的泛化能力和回归精度。训练参数的选取，将直接影响映射模型的精度及其泛化能力，本文采用遗传算法在全局范围内进行参数寻优。
3.2.2 遗传算法参数寻优遗传算法的操作对象是一群染色体，每个染色体对应问题的一个解。从初始种群出发，采用基于适应度函数的选择策略在当前种群中选择个体，通过遗传算子操作产生下一代种群，不断演化直到满足期望的终止条件。将参数γ、C表示为适于遗传算法求解的两个染色体问题，寻找其最优值，计算步骤如下[26]：
(1) 参数编码。为避免联系状态之间转换时可能出现的逻辑混淆，采用二进制雷格码编码。
(2) 生成初始群体。设定参数的取值范围0≤γ≤1000,0＜C≤500，随机产生染色体数量为20，变量数为2(即核函数参数γ和惩罚参数C)，染色体用20位雷格码表示。
(3) 计算个体适应度函数值。适应度函数式是遗传算法优化的依据，用于评价个体优劣程度。采用交叉验证法和线性排序分配适应度函数值。
(4) 对个体进行遗传算子操作。采用适应度比例方法进行选择运算，交叉运算概率设为0.7，变异运算概率设为0.05，生成子代群体。
(5) 判断是否满足终止条件(相邻两次精度差小于0.001)，若满足则停止计算解码输出优化解，否则将子代染色体代替父染色体转入步骤(3)。
3.3 GA-SVR预测次优观测值
假设GPS/INS组合系统整体异常前一时刻tk，GPS位置为Pk，基于GA-SVR训练的回归模型采样间隔为Δt。下一时刻tk+1(tk+1=tk+Δt)，检测出现异常，利用已训练好的GA-SVR回归模型和速度vt、姿态φt、加速度增量、姿态角度增量回归出GPS位移增量ΔPk，此时预测观测值坐标Pk+1为：Pk+1=Pk+ΔPk 。
在中国矿业大学南湖校区采集4000s DGPS(1Hz)和IMU(100Hz)数据，仪器采用Leica 1200 Base & Rover GPS System和SPAN-CPT。其中DGPS测量值点位精度为厘米级，北东高方向观测误差分别为0.05m、0.05m和0.1m；INS北东高初始位置误差分别为1m、1m和2m；北东高初始速度为0.5m/s；俯仰翻滚和航向初始姿态误差分别为1°、1°和3°；陀螺漂移和加速度偏置误差分别为5°/h和50μg；陀螺仪和加速度相关时间分别为100s和60s。
4.1 GA-SVR预测GPS位置增量为验证GA-SVR算法预测GPS位移增量的精度，以1～600s数据作为样本训练，其中INS速度、姿态、加速度增量、姿态增量为训练输入，GPS位置增量为训练输出，构建支持向量回归模型预测601～4000s的GPS位置增量。
图 3为采用遗传算法寻找支持向量回归训练最优参数(核函数参数γ和惩罚参数C)的100次进化过程。令相邻两次进化精度差值小于0.001即为收敛，纬度、经度和高程方向分别迭代46次、94次和3次后收敛，其中GPS位移增量幅度最小的高程方向上收敛速度最快，而GPS位移增量幅度最大的东方向收敛速度最慢，收敛后最优训练参数如表 1所示。
|
| 图 3 遗传算法适应度曲线 Fig. 3 Genetic algorithm fitness curves |
| 方向 | GA参数寻优 | 支持 | 偏差 | 训练数据 | 预测数据 | |
| C | γ | 向量数 | 项 | 均方差/m | 均方差/m | |
| 纬度 | 5.281 | 0.253 | 153 | -0.452 | 0.184 | 0.233 |
| 经度 | 49.784 | 0.050 | 109 | -0.543 | 0.108 | 0.176 |
| 高程 | 7.890 | 128.125 | 311 | -0.506 | 0.037 | 0.148 |
采用遗传算法寻优得到的参数，基于支持向量机回归原理对训练数据进行训练学习，构造回归模型式(13)，计算得到纬度、经度和高程方向153、109和311个支持向量及其偏置项如表 1所示。图 4(a)、(b)、(c)分别为GA-SVR算法在纬度、经度和高程训练和预测结果，其中训练数据在纬度、经度和高程均方差分别为0.184m、0.108m、0.037m，预测数据在纬度、经度和高程均方差分别为0.233m、0.176m、0.148m，表明GA-SVR算法能预测出亚分米级精度的GPS坐标值。
|
| 图 4 GA-SVR训练回归结果 Fig. 4 GA-SVR training results |
为验证GA-SVR算法辅助组合导航抗差自适应滤波算法的有效性，在实测数据中人为加入以下两种故障：①GPS观测值高程方向，1600～2500s之间每隔100s分别增加2m、4m、6m、8m、10m、20m、20m、20m、20m、20m的观测粗差。②INS观测值加速度计高方向，2100～3000s之间每隔100s分别增加10m/s2、9m/s2、8m/s2、7m/s2、6m/s2、5m/s2、4m/s2、3m/s2、2m/s2、1m/s2的状态异常。其中1600～2000s之间存在观测异常，2100～2500s之间存在观测异常和状态异常，2600～3000s之间存在状态异常。
同时设计以下方案与标准EKF算法解算结果进行比对：①抗差EKF算法(REKF)；②自适应EKF算法(AEKF)；③RAEKF 算法(RAEKF)；④GA-SVR辅助EKF 算法(SVR-RAEKF)。结果如图 5—图 8所示。
|
| 图 5 REKF和EKF算法在高程上位置误差 Fig. 5 Height position errors of REKF and EKF |
|
| 图 6 AEKF和EKF算法在高程上位置误差 Fig. 6 Height position errors of AEKF and EKF |
|
| 图 7 RAEKF和EKF算法在高程上位置误差 Fig. 7 Height position errors of RAEKF and EKF |
|
| 图 8 GA-SVR辅助RAEKF和EKF算法在高程上位置误差 Fig. 8 Height position errors of GA-SVR aided RAEKF and EKF |
分析上述结果，可以看出：
(1) 标准EKF算法结果显示，1600～2000s之间误差随着观测粗差不断增大而递增；2100～2500s之间在相同的观测粗差和递减的状态异常共同作用下误差达到最大且呈递减趋势；随着观测粗差在2500 s之后消失误差不规则突然变小，2600～3000 s之间随着状态异常递减而递减。误差与加入的粗差在趋势上保持一致，表明EKF算法无法应对滤波异常。
(2) 由图 5可知，抗差EKF算法能够减弱单独观测粗差的影响(1600～2000s)，导航解精度较好，但对存在观测异常和状态异常(2100～2500s)、状态异常(2600～3000s)的历元的导航解，抗差EKF算法解算结果精度较低。
(3) 由图 6可知，自适应EKF滤波对观测值极为敏感，通过调节状态协方差，消除状态异常影响(2600～3000s)，使其与观测值保持一致，导航解精度较高。但对存在观测异常(1600～2500s)的历元，导航解精度较低。
(4) 由图 7可知，由于无法区分观测异常和状态异常导致误判，抗差自适应EKF产生较多低精度导航解。由图 8可知，GA-SVR结合整体异常检测能判断出异常原因，智能选取抗差自适应算法，即观测粗差存在采用抗差EKF，状态异常存在采用自适应EKF，观测异常和状态异常都存在采用基于预测观测值的自适应EKF。但可以看出，虽然因GA-SVR预测精度导致结果出现个别较小误差(椭圆标出)，GA-SVR辅助的抗差自适应滤波算法能够更好地减弱观测异常和状态异常影响，提供可靠的导航解。
4.3 导航实时性分析计算效率和时效性对实时导航至关重要，抗差自适应算法、GA参数寻优、SVR模型训练与预测等势必增加导航系统计算量。GA-SVR辅助抗差自适应滤波算法中的计算量增加主要是由3部分造成：①基于GA在全局范围内对支持向量回归模型最优参数的搜索；②SVR模型训练与预测；③自适应因子和抗差因子迭代计算。其中，SVR模型训练与预测、迭代求自适应因子和抗差因子的计算量很小，对导航解的实时性影响较小。而基于GA参数寻优耗时较长，对导航解的实时性影响较大，但基于遗传算法在全局范围内对支持向量回归模型最优参数的搜索可以根据事先采集的数据提前确定，导航时直接采用该最优参数。
基于GA提前确定SVR模型参数后，相同运算环境下使用同一台计算机对1600～2500s之间加入异常的历元数据进行解算，表 2为常规EKF和GA-SVR辅助的RAEKF两种算法的解算耗时数据。由于IMU试验数据采用率为100Hz，为了不影响导航实时性，要求每个历元滤波解算最大耗时不超过10ms。表中实时性影响比率为GA-SVR辅助算法导致增加的计算量占最大耗时要求的比重。可以看出：GA-SVR预测观测值辅助RAEKF算法平均耗时为3.249ms，最大值7.770ms，均小于最大耗时要求；增加的计算量占最大耗时要求平均26.69%，最大为69.76%，虽不影响导航实时性，但仍有进一步优化的必要。
| 历元 |
| 实时性影响 /(%) |
| 1600 | 2.508 | 4.417 | 19.09 |
| 1700 | 0.44 | 4.046 | 36.06 |
| 1800 | 0.392 | 3.97 | 35.78 |
| 1900 | 0.388 | 3.825 | 34.37 |
| 2000 | 0.454 | 3.719 | 32.65 |
| 2100 | 0.794 | 7.77 | 69.76 |
| 2200 | 0.44 | 0.825 | 3.85 |
| 2300 | 0.467 | 0.711 | 2.44 |
| 2400 | 0.37 | 0.636 | 2.66 |
| 2500 | 0.399 | 5.579 | 51.8 |
| 2600 | 0.392 | 5.398 | 50.06 |
| 2700 | 0.394 | 0.703 | 3.09 |
| 2800 | 0.439 | 5.904 | 54.65 |
| 2900 | 0.392 | 0.573 | 1.81 |
| 3000 | 0.435 | 0.661 | 2.26 |
| 统计 分析 |
|
本文在常规EKF滤波基础上，采用预测状态协方差矩阵和观测向量预测残差构造抗差和自适应因子。基于GA-SVR算法预测出可靠的位置，结合整体异常检测，精确判定异常来源，智能选取抗差自适应滤波方法，给出计算步骤。利用实测数据，加入观测粗差、状态异常及观测粗差和状态异常并存混合故障，通过对比多种算法并进行误差分析，验证算法的有效性，从而为组合导航提供了一种可行的思路。基于遗传算法寻找支持向量训练机最优参数的过程比较耗时，对于计算性能不高的组合系统，可能会影响到导航的实时性，可以根据经验和仪器参数提前训练得出最优参数和回归模型。
| [1] | YANG Y X, HE H B, XU G C. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2):109-116. |
| [2] | YANG Yuanxi. Adaptive Kinematic Navigation and Positioning[M]. Beijing: Surveying and Mapping Press,2006:79-99. (杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006:79-99.) |
| [3] | BRUMBACK B, SRINATH M. A Chi-square Test for Fault Detection in Kalman Filter[J]. IEEE Transactions on Automatic Control, 1987, 32(6): 552-554. |
| [4] | DA R, LIN C F. Sensitivity Analysis Algorithm for the State Chi-square Test[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(1): 219-222. |
| [5] | CHEN J, PATTON R J. Robust Model Based Fault Diagnosis for Dynamic System[M]. Norwell: Kluwer Academic Publishers, 1999:15-20. |
| [6] | YANG Y X, GAO W G. A New Learning Statistic for Adaptive Filter Based on Predicted Residuals [J]. Progress in Natural Science, 2006, 16(8): 833-837. |
| [7] | YU Xuexiang, LV Weicai. Robust Kalman Filtering Model and Its Application in GPS Monitoring Networks[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 27-31.(余学祥,吕伟才.抗差卡尔曼滤波模型及其在GPS监测网中的应用[J].测绘学报, 2001, 30(1): 27-31.) |
| [8] | YANG Yuanxi, ZHANG Shuangcheng. Fittings of Systematic Errors and Covariance Matrices in Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 189-194.(杨元喜,张双成.导航解算中的系统误差及其协方差矩阵拟合[J].测绘学报, 2004, 33(3): 189-194.) |
| [9] | LI Bofeng, SHEN Yunzhong. Equivalent Residual Product Based Outlier Detection for Variance and Covariance Component Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 10-14.(李博峰,沈云中.基于等效残差积探测粗差的方差-协方差分量估计[J].测绘学报, 2011, 40(1): 10-14.) |
| [10] | YANG Y X, GAO W G. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. |
| [11] | WANG Jian, LIU Chao, GAO Jingxiang. GNSS/INS Tightly Coupled Navigation Based on Robust EKF Algorithm [J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):596-599. |
| [12] | MASSOUMNIA M. A Geometric Approach to the Synthesis of Failure Detection Filters[J]. IEEE Transactions on Automatic Control, 1986, 31(9): 839-846. |
| [13] | WANG J J, WANG J, SINCLAIR D, et al. A Neural Network and Kalman Filter Hybrid Approach for GPS/INS Integration[C]//Symposium of the 12th IAIN Congress on GPS/GNSS. Jeju:[s.n.],2006: 18-20. |
| [14] | NOURELDIN A, OSMAN A, EL-SHEIMY N. A Neuro-wavelet Method for Multi-sensor System Integration for Vehicular Navigation[J]. Measurement Science and Technology, 2004, 15(2): 404-412. |
| [15] | SEMENIUK L, NOURELDIN A. Bridging GPS Outages Using Neural Network Estimates of INS Position and Velocity Errors[J]. Measurement Science and Technology, 2006, 17 (9): 2782-2798. |
| [16] | ABD-ELHAMID W, NOURELDIN A, EL-SHEIMY N. Adaptive Fuzzy Modeling of Low Cost Inertial Based Positioning Errors[J]. IEEE Transactions on Fuzzy Systems, 2007, 15 (3): 519-529. |
| [17] | KAYGISIZ, BURAK H, ERKMEN, et al. Enhancing Positioning Accuracy of GPS/INS System during GPS Outages Utilizing Artificial Neural Network[J]. Neural Processing Letters, 2007, 25(3): 171-186. |
| [18] | GAO Weiguang, YANG Yuanxi. Neural Network Aided GPS/INS Integrated Navigation Fault Detection Algorithms[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 403-409. (高为广,杨元喜. 神经网络辅助的GPS/INS组合导航故障检测算法[J].测绘学报, 2008, 37(4): 403-409.) |
| [19] | XU Z, LI Y, RIZOS C, et al. Novel Hybrid of LS-SVM and Kalman Filter for GPS/INS Integration[J]. Journal of Navigation, 2010, 63(2): 289-298. |
| [20] | WANG Jianguo. Integration of GPS, INS and Pseudolite to Geo-reference Surveying and Mapping Systems[D]. Sydney: University of Sydney, 2007. |
| [21] | LIU Guangjun, WU Xiaoping, GUO Jing. A Numerically Stable Sub-optimal Parallel Sage Adaptive Filter[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 283-288.(刘广军,吴晓平,郭晶.一种数值稳定的次优并行Sage自适应滤波器[J].测绘学报, 2002, 31(4): 283-288.) |
| [22] | YANG Yuanxi,GAO Weiguang. A New Learning Statistic for Adaptive Filter Based on Predicted Residuals[J].Progress in Natural Science,2006,16(8):833-837. |
| [23] | OU Jikun. Design of a New Scheme of Robust Estimation by Three Steps[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 173-179.(欧吉坤.一种三步抗差方案的设计[J].测绘学报, 1996, 25(3): 173-179.) |
| [24] | VAPNIK V. The Nature of Statistical Learning Theory[M]. [S.l.]:Springer, 2000:31-38. |
| [25] | STEINWART I, CHRISTMANN A. Support Vector Machines[M]. [S.l.]:Springer, 2008:42-47. |
| [26] | BCK T, SCHWEFEL H P. An Overview of Evolutionary Algorithms for Parameter Optimization[J]. Evolutionary Computation, 1993, 1(1): 1-23. |