2. 中国科学院 地理科学与资源研究所 资源与环境信息系统国家重点实验室,北京 100101;
3. 中国科学院大学,北京 100049;
4. 山东科技大学 测绘科学与工程学院,山东 青岛 266590
2. State Key Laboratory of Resources and Environmental Information System,Institute of Geographic and Nature Resources Research,Chinese Academy of Sciences,Beijing 100101,China;
3. University of Chinese Academy of Sciences,Beijing 100049,China;
4. College of Geomatics,Shandong University of Science and Technology,Qingdao 266510,China
1 引 言
空间数据规模的快速膨胀给现有的计算资源和传统的地学计算方法带来了前所未有的压力,高性能计算已成为解决海量空间数据分析、处理以及大规模空间可视化的重要手段[1, 2]。集群环境下基于消息传递接口(message passing interface,MPI)的并行计算模式得到了充分的重视和发展,已有的并行化空间分析算法大多基于该架构实现。数据划分和任务分解是实现并行计算的两种主要模式[3],目前高性能空间分析算法的研究仍然以数据并行方式为主[4]。许多学者对带有拓扑关系的空间分析并行算法的任务划分进行了研究[5, 6, 7],本文选择基于更利于实现并行任务分解的OGC简单要素模型开展对缓冲区算法开发和优化的研究。
缓冲区处理的是一类邻近度问题,代表了一种影响范围或服务范围,是地图信息检索与综合处理和GIS 空间分析的重要功能[8, 9]。以往针对缓冲区分析算法的研究多面向缓冲区域的生成算法展开,例如文献[9]提出了双线生成的几何算法模型和针对自相交问题的关系处理模型。文献[11]详细描述了线段集合的非对称缓冲区生成算法,文献[12]基于文献[11]的线段缓冲区生成算法,实现了采用扫描线思想和向量代数的缓冲区生成和结果多边形融合算法。文献[13]提出了一种基于缓冲曲线和边约束三角网辅助的矢量缓冲区生成算法。文献[14]基于“条带扫描”思想实现了复杂线目标缓冲区的构建和效率优化。虽然上述基于矢量计算方法的缓冲区生成算法可以得到较为精确的结果,但是需要诸多复杂的计算和空间关系判断,实现过程较为复杂。文献[15]提出了基于膨胀算法的缓冲区生成算法,其本质是利用栅格化的思想简化矢量缓冲区生成的过程,但该算法不可避免地带来误差。缓冲区分析算法同样面临大数据量背景下的效率提升问题。文献[16]在网格环境下利用分布式并行计算来加速缓冲区分析算法,但网格计算注重于异构计算环境下的分布式处理,且难以达到高性能计算的目的。
几何部件缓冲区域合并的本质是多边形合并,基于多边形裁剪算法实现。目前公认的能在有限时间内完成任意多边形裁剪问题的有效算法主要有Vatti算法[17]和Greiner-Hormann算法[19]等。Vatti算法是对文献[20, 21]所提出多边形裁剪算法的重大改进,本文基于Vatti算法实现多边形合并操作。目前一些商业GIS软件的缓冲区分析工具的计算效率难以让人满意,且MPI环境下缓冲区算法的并行化及优化方法的研究较少,因此大数据量应用背景下的并行缓冲区算法及其优化方法值得深入研究。
本文组织结构为:首先给出基于几何部件缓冲区域合并的Buffer串行算法,进而比较该算法与ArcGIS Buffer工具在缓冲区结果多边形合并与不合并两种条件下的效率差异;其次基于数据并行的思想实现缓冲区分析的并行算法并分析其加速性能表现;最后通过分析并行缓冲区分析算法的执行过程,指出并行算法可能存在的性能瓶颈并提出对应的优化方案并进行试验验证。
2 基于几何部件缓冲区域合并的Buffer算法 2.1 几何对象缓冲区构造方法矢量缓冲区生成算法包括平行线生成、构环和空间关系处理3个步骤,其中构环和空间关系处理过程包含大量的复杂数值计算,如交点计算、向量和夹角计算,自相交处理等,涉及多种特殊情况,实现较为困难。本文将成熟的多边形裁剪算法引入矢量缓冲区的生成过程,用来代替复杂的构环和空间关系处理等过程,实现对缓冲区生成算法的简化处理。单侧缓冲区生成较为简单,且非对称缓冲区可采用双侧区分处理、端点圆弧圆心平移的方法实现,因此本研究仅讨论最为典型的双侧、对称缓冲区的生成方法。下面分别描述点、线和多边形3种基本几何对象的缓冲区构造方法,如图 1所示。
|
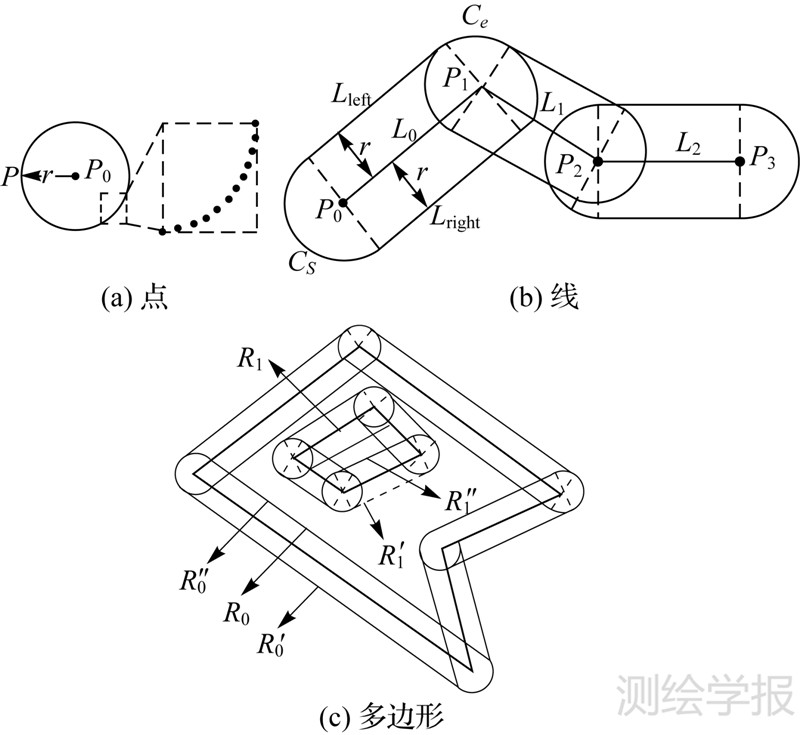
| 图 1 点、线、多边形的缓冲区构建 Fig. 1 Buffer zone construction of point,line and polygon |
如图 1(a)所示,点P0以r为半径的缓冲区域构造方法为:以P0为圆心以r为半径绘制首尾相连的圆环。实际仅需计算圆环落在以P0为原点的直角坐标系第一象限内的点,其他象限内点的坐标均可由对称性计算得到。求出圆环上所有点的坐标后,顺时针依次连接即构成闭合的环,即为点P0以r为半径的缓冲区域。增加点数量对圆环进行加密即可得到更为平滑的缓冲区边界。对于由多个单点部件构成的多点几何对象,构成它的每个点均按照单点几何对象缓冲区的生成规则构建各自的缓冲区域,结果可能将出现重叠,通过调用多边形合并操作实现重叠区域的融合,得到合并后的多点几何对象的缓冲区图形。
2.1.2 线线类型的几何对象可看作是一组首尾相连的线段组,每条线段由两个点部件构成:起点和终点。如图 1(b)所示,折线L由L0、L1和L2 3条线段构成,L的缓冲区由构成它的每条线段的缓冲区通过多边形合并操作得到。而线段的缓冲区生成过程包括3个步骤,以线段L0为例进行说明:首先是求L0两侧距离为r的平行线Lleft和Lright;然后分别以L0起点P0和终点P1为圆心做半圆弧Cs和Ce;最后顺次连接左侧平行线Lleft、起点半圆弧Cs、右侧平行线Lright和终点半圆弧Ce,得到线段L0的半径为r的缓冲区域。
由于折线的缓冲区由构成折线所有线段的缓冲区多边形合并而来,而线段缓冲区为两端均为半圆形的多边形,因此相连线段的缓冲区多边形在公共点处同为圆心重合的半圆形,因此当相连线段不共线时将在沿着折线方向的折点反角一侧形成弧形边界。如图 1(b)所示,沿L0→L1→L2方向的P1左侧和P2右侧均为弧形边界。由多条折线部件构成的几何对象称为多线,只需将构成多线的每条折线的缓冲区结果合并即可得到多线几何对象的缓冲区。
2.1.3 多边形多边形可看作由一组首尾闭合的折线包围而成的面状区域,闭合的折线称为环,根据构成环的点的走向不同分为内环和外环。简单多边形指的是仅包含一个外环和若干个内环的多边形,包含了多个外环的多边形称为多多边形,同样,多多边形的缓冲区域可由构成它的每个简单多边形的缓冲区合并得到。基于几何部件缓冲区域合并的简单多边形的缓冲区生成过程由分解、构环、合并和剔除4个步骤组成。首先是对输入多边形的环进行分解,得到一组折线,然后对每条折线按照图 1(b)所示方法构造独立的缓冲区多边形,再将折线缓冲区合并,最后对新生成的环进行选择性剔除。双侧缓冲区生成的剔除规则为:保留外环生成的外环和内环生成的内环,其他均删除。
如图 1(c)所示,输入多边形由外环R0和内环R1构成,分别将其在起点/终点处打断后按照折线缓冲区生成方法构建缓冲区域,得到R′0、R″0、R′1、R″1共4个环,按照上述规则,保留外环R0生成的外环R′0和内环R1生成的内环R″1,删除R″0和R′1,最后生成得到仅包含了环R′0和R″1的结果多边形。在构建内环的内侧缓冲区时若合并后的缓冲区多边形的内环消失,说明缓冲区半径超过了内环可容纳的缓冲范围,此时将内环生成的所有环丢弃,多边形的缓冲区边界同样会出现弧形边界部分。
2.2 串行算法性能分析基于几何部件缓冲区域合并的矢量数据缓冲区生成算法在处理线状几何对象时最为典型。为分析不同数据量下该算法的串行性能表现,本文基于不同规模的真实路网线状数据集开展了相关试验,试验数据如图 2所示。缓冲区多边形生成完成后的合并过程中,本文采用R树空间索引[22]实现相交多边形的预筛选来过滤掉不相交的多边形,这种考虑到几何要素间空间关系的预筛选策略能有效减少多边形合并操作的调用次数,提高算法效率。

|
| 图 2 试验数据及缓冲区结果实例 Fig. 2 Sample of experimental data and buffer results |
本研究中试验平台为Dell OPTIPLEX 990计算机,配备主频为3.4 GHz的Intel i7-2600 4核8线程CPU,4 G内存,操作系统为Fedora Linux 15(运行MPI程序)/Windows 7(运行ArcGIS程序),本文在相同硬件平台上与ArcGIS 9.3/10.1SP1版本下的串行Buffer工具进行了对比,试验结果列于表 1中。
| 线数量 | 节点数量 | 时间(不合并)/s | 时间(相交合并)/s | |||
| 本文算法 | ArcGIS 9.3/10.1 | 本文算法 | ArcGIS 9.3/10.1 | |||
| 1 950 | 24 012 | 1.030 | <1.00/<1.00 | 1.677 | 10.50/42.00 | |
| 13 324 | 147 824 | 6.911 | 4.00/3.67 | 13.291 | 189.00/2 053.00 | |
| 33 205 | 318 590 | 14.547 | 9.33/7.60 | 32.098 | 787.00/- | |
| 45 850 | 470 825 | 21.544 | 13.67/10.50 | 57.885 | 1 243.50/- | |
| 108 414 | 1 067 682 | 52.097 | 31.33/25.00 | 128.545 | 3 676.50/- | |
由表 1可知,当相交的缓冲区结果多边形不合并时,本文的缓冲区算法效率不及ArcGIS Buffer 工具,效率平均相差0.7~1倍。但是当合并相交的缓冲区结果多边形时,ArcGIS 10.1 SP1版本花费了超过10 h却未得到结果,而其9.3版本虽然能得到结果,但时间开销比本文的缓冲区分析算法要多得多,且本文算法所体现出的性能优势随数据量的增加而更加显著。因此,本文认为基于几何部件缓冲区域合并的Buffer算法不仅可用,而且能有效解决目前商业GIS软件中缓冲区分析合并过程中的严重性能瓶颈。
3 基于MPI的并行缓冲区生成算法 3.1 并行算法的逻辑流程高性能计算技术是解决缓冲区分析中遇到的海量数据处理难题的有力工具,但必须对其实现和优化方法进行研究。并行缓冲区分析算法的逻辑流程包括了4个主要环节,分别是任务划分、并行构建缓冲区、缓冲区多边形合并和结果数据输出,上述4个环节分别对应分解、计算、合并和输出4个步骤。
3.2 并行算法性能本文按照上述逻辑流程设计并实现了基于MPI编程模型及数据并行思想的并行缓冲区分析算法,并采用与图 4类似的多组线状真实路网数据开展试验,结果在表 2中列出。
|
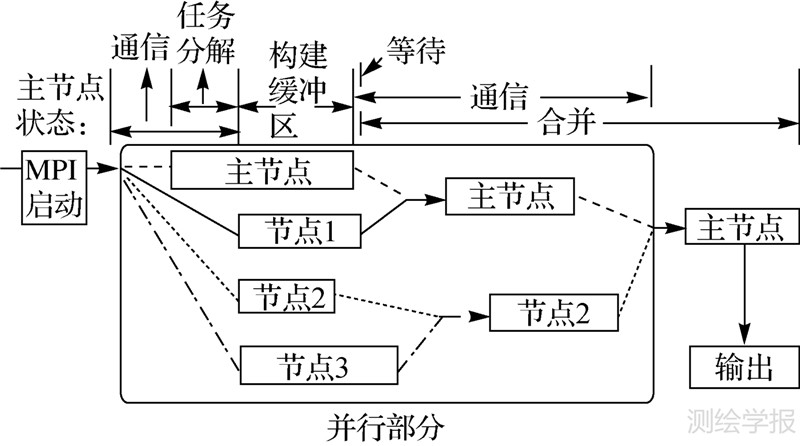
| 图 4 缓冲区分析结果的“树状”归并合并流程(4个MPI进程) Fig. 4 Tree-like merging flow of buffer results(4 MPI processes) |
| 线数量 | 节点数量 | 不同进程数时间开销(不合并)/s | 不同进程数时间开销(相交合并)/s | |||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||
| 1 950 | 24 012 | 1.342 | 1.209 | 1.161 | 1.288 | 1.426 | 1.225 | 1.091 | 1.255 | |
| 13 324 | 147 824 | 8.959 | 6.070 | 5.059 | 4.667 | 11.191 | 8.046 | 8.280 | 7.217 | |
| 33 205 | 318 590 | 19.723 | 12.964 | 11.211 | 10.092 | 26.802 | 21.248 | 18.881 | 17.756 | |
| 45 850 | 470 825 | 26.797 | 17.671 | 16.338 | 14.976 | 56.901 | 52.758 | 55.062 | 52.350 | |
| 108 414 | 1 067 682 | 68.113 | 39.048 | 34.747 | 33.324 | 126.907 | 105.749 | 109.755 | 109.927 | |
| 134 145 | 1 482 071 | 86.318 | 49.955 | 44.208 | 43.016 | 243.110 | 214.180 | 211.997 | 224.911 | |
| 269 450 | 3 231 870 | 192.465 | 106.241 | 93.741 | 84.229 | 494.808 | 368.687 | 418.435 | 442.850 | |
由表 2可知,基于MPI和多边形合并的并行缓冲区算法可以得到一定的并行加速,且当缓冲区结果多边形不需合并时,采用4个进程得到了与ArcGIS相近的计算效率,但其加速比并不理想,当进程数增多时并行计算效率甚至出现了下降趋势,这说明并行缓冲区算法存在进一步优化的空间,应分析其性能瓶颈并加以优化消除。
3.3 并行缓冲区算法瓶颈分析实现高性能计算的一个无法回避的问题是如何平衡各个并行任务间的负载,因为只有达到了负载平衡才能使所有的计算任务在相近的时间内完成,这对在基于MPI实现的集群并行计算环境中运行的并行缓冲区算法尤为重要,因为只有使率先完成计算任务的MPI进程的合并操作的启动前等待时间最短,集群系统的综合利用率才能得到提升。本文开展了两次按照要素序列(feature ID,FID)进行数据分割以实现并行任务分配的并行缓冲区分析试验,并统计了速度相差最大的两个进程的分步时间开销,试验结果在表 3中列出。
| 进程/要素数量 | 单进程时间开销/s | 单进程数据量 | ||||
| 构建缓冲区 | 合并 | 要素数量 | 点数量 | |||
| 4/134 145 | 最快 | 9.284 | 9.073 | 33 536 | 256 908 | |
| 最慢 | 20.150 | 57.449 | 33 537 | 492 465 | ||
| 8/269 450 | 最快 | 21.491 | 7.833 | 33 681 | 313 627 | |
| 最慢 | 37.772 | 91.226 | 33 683 | 547 461 | ||
由表 3可知,虽然基于要素序列的任务划分方法能够实现不同MPI进程间要素个数的平均分配,但是不同进程间的矢量要素所包含的节点数量可能差异巨大,而基于Vatti算法实现的多边形合并操作对节点数量敏感,基于该算法实现的缓冲区算法必然受其影响,这导致了进程间任务负载的不均衡,直接后果是不同进程间计算时间存在较大差异,最慢的进程时间开销约是最快者的2.2倍,最慢者的合并时间约是最快者的11.6倍。因此,数据分割不合理易带来不均衡的任务负载,从而造成MPI并行算法潜在的性能瓶颈,对数据并行模式下的并行任务的均匀分解是实现MPI进程间负载均衡的前提条件,也是对并行算法进行优化的重要方向。
此外,不同进程的计算时间存在差异,在无法达到负载平衡时尤为明显,这导致先计算完毕的进程需要等待其他未完成的进程,如果进程间结果归并的任务被分配给单一进程统一执行,该进程需要等待其他所有进程全部执行完毕后才能继续结果归并的任务,这显然降低了并行系统的利用率,带来性能瓶颈。根据最大限度降低MPI进程间的互相等待时间的基本原则,需要重新设计MPI进程间结果集合的归并策略。
4 并行缓冲区算法优化 4.1 并行任务分解要素序列分割方法能保证分配到每个计算节点上的要素数量大致相等,但却无法保证各个计算节点负担的计算量的均衡。针对并行矢量缓冲区结果合并算子对多边形点数敏感的特点,本文提出基于点数统计的并行任务数据分解方法。该方法以几何对象所包含的节点数作为数据分组的依据,假设一组输入数据共包含N个节点,并行环境中有n个MPI进程,则预期每个进程将被分配到一组共包含P个节点的矢量要素,P约为N/n,分配到每个进程上的要素数量不再固定。在MPI进程数恒定为4,且算法其他特征保持一致的前提下,本文对7组不同数据量的路网数据分别进行了基于要素序列分割以及点数分割的缓冲区分析试验,结果在表 4中列出。
| 要素/节点数量 | 时间开销(4个MPI进程)T/s | ||
| TFIDs | Tpoints | TDP | |
| 13 324/147 824 | 7.517 | 6.558 | 0.042 |
| 18 154/215 048 | 14.043 | 11.618 | 0.101 |
| 33 205/318 590 | 18.267 | 15.594 | 0.103 |
| 45 850/470 825 | 52.023 | 46.478 | 0.142 |
| 108 414/1 067 682 | 110.365 | 101.155 | 0.396 |
| 134 145/1 482 071 | 224.633 | 204.446 | 0.429 |
| 269 450/3 231 870 | 430.176 | 419.370 | 1.379 |
表 4中,TFIDs为按要素序列分割的并行算法总时间;Tpoints为按照点数分割的并行算法总时间;TDP为按点数分割数据的数据划分过程所花费的时间,已包含在Tpoints中。试验结果表明,点数分割方法平均以约0.43%的时间开销代价获得了高于10%的性能提升,因此该方法能够提升并行矢量缓冲区算法的计算效率。
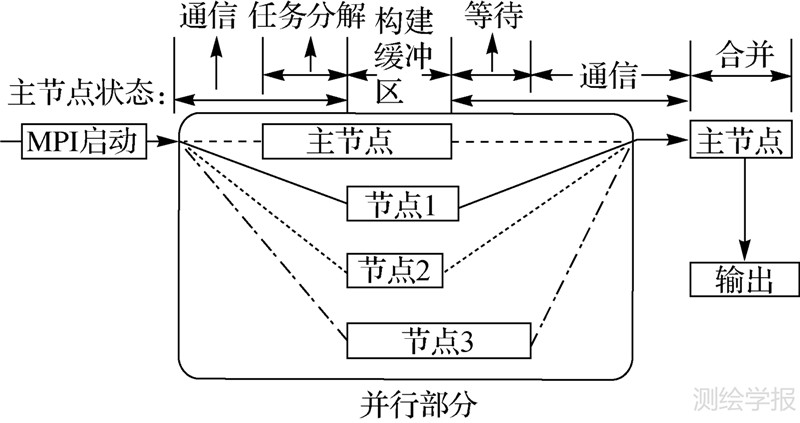
4.2 MPI进程间“树状”归并优化当多个并行执行的MPI进程执行完毕后,不同进程生成的结果多边形集合同样需要进行相交判断和合并,一种直接的处理方式是将所有结果全部交由单一进程实现合并和输出,其执行流程如图 3所示,该策略的显著缺点是负责合并输出的进程必须等待所有进程全部执行完毕后才能最终开始执行并完成合并输出的操作。
|
| 图 3 缓冲区分析结果的单一进程合并流程(4个MPI进程) Fig. 3 Single-process merging flow of buffer results (4 MPI processes) |
结合多边形合并过程中所采用的分治策略,本研究中为进程间结果集合的归并设计了一种新的策略,通过最大限度缩短进程间等待时间来实现算法加速,本文称其为MPI进程间“树状”归并优化策略,其流程如图 4所示。
以图 4中的4个MPI进程为例进行说明:规定第1个进程和第2个进程归并,结果由第1个进程保持和处理,第3和第4归并,结果由第3个进程保持和处理,然后第1个和第3个进程将前两次归并的结果再次归并,依次类推。这样通过为多个MPI并行进程预先规划出一条“树状”归并路径可降低MPI程序开发的难度。本文实现了具有上述结果归并流程的并行缓冲区算法,为与单一进程归并模式的并行缓冲区算法进行对比,在保持算法其他特征一致的前提下,采用7组不同数据量的路网数据开展了相关试验,结果在表 5中列出。
| 要素/节点数量 | 并行时间开销 (4个MPI进程)/s | 串行算法 | 加速比 | 效率提升比率/(%) | |
| 单一进程合并 | “树状”归并合并 | ||||
| 13 324/147 824 | 6.432 | 5.503 | 11.288 | 2.051 | 16.9 |
| 33 205/318 590 | 15.691 | 10.499 | 27.067 | 2.578 | 33.1 |
| 45 850/470 825 | 46.747 | 21.909 | 57.271 | 2.614 | 53.1 |
| 108 414/1 067 682 | 100.939 | 44.612 | 127.707 | 2.863 | 55.8 |
| 134 145/1 482 071 | 198.670 | 78.781 | 243.979 | 3.097 | 60.3 |
| 269 450/3 231 870 | 419.306 | 172.288 | 499.723 | 2.901 | 58.9 |
| 1 329 758/12 471 234 | 1 685.036 | 878.841 | 2 509.740 | 2.856 | 47.8 |
| 平均 | - | - | - | 2.708 | 46.6 |
由表 5可知,MPI进程间结果“树状”归并优化可为并行缓冲区分析算法带来平均约46.6%的效率提升,4个MPI进程下的并行加速比从1.411提升至2.708,优化效果显著。因此,MPI进程间多边形集合的“树状”归并方法对并行缓冲区分析算法具有明显的优化效果。
5 结 论本文在描述一种可用的基于几何部件缓冲区域合并思想的矢量缓冲区生成算法的基础上,基于MPI并行编程模型实现了并行缓冲区生成算法,并详细分析了可能导致其效率低下的两处性能瓶颈,分别提出了优化解决方案:针对并行任务负载均衡问题的按节点数量进行并行任务分割的方法和MPI进程间结果集合的“树状”归并方法。试验结果表明,点数分割方法平均以约0.43%的时间开销代价获得了高于10%的性能提升;MPI进程间结果集合的“树状”归并优化可为并行缓冲区分析算法带来平均约46.6%的效率提升,4个MPI进程下的并行加速比从1.411提升至2.708,优化效果显著。因此,基于几何部件缓冲区域合并的矢量数据缓冲区生成算法具有一定的实用价值,两种优化方法能有效改善缓冲区分析算法的性能表现,是对缓冲区分析算法进行并行化和优化改进的有效途径。
此外,MPI进程间结果集合的归并模式可以采用更为合理的“先完成先归并”的自适应方式,将有可能获得更为优秀的并行优化效果,但这将导致编程复杂度大大提高,是下一步的研究方向。
| [1] | TURTONI, OPENSHAW S. High-performance Computing and Geography: Developments, Issues, and Case Studies[J]. Environment and Planning: A,1998, 30: 1839-1856. |
| [2] | CLARKE K C. Geocomputation’s Future at the Extremes: High Performance Computing and Nanoclients[J]. Parallel Computing, 2003, 29(10): 1281-1295. |
| [3] | GRAMA A, GUPTA A, KARYPIS G, et al.Introduction to Parallel Computing [M]. Boston: AddisonWesley, 2003: 85-142. |
| [4] | WANG Jiechen, WANG Bao, HU Wei, et al.Review on Parallel Spatial Analysis Algorithms[J]. Geography and Geo-Information Science, 2011, 27(6): 1-5. (王结臣, 王豹, 胡玮, 等. 并行空间分析算法研究进展及评述[J]. 地理与地理信息科学, 2011, 27(6): 1-5.) |
| [5] | SLOAN T M, MINETERM J, DOWERS S, et al.Partitioning of Vector-topological Data for Parallel GIS Operations: Assessment and Performance Analysis[C]//Proceedings of Euro-Par′99 Parallel Processing, Lecture Notes in Computer Science. Delft:[s.n.],1999: 691-694. |
| [6] | MINETERM J, DOWERS S. Parallel Processing for Geographical Applications: A Layered Approach[J]. Journal of Geographical Systems, 1999, 1(1): 61-74. |
| [7] | DARLING G J, SLOAN T M, MULHOLLAND C. The Input, Preparation and Distribution of Data for Parallel GIS Operations[C]//Proceedings of Euro-Par 2000,Lecture Notes in Computer Science. Ischia :[s.n.],2000:500-505. |
| [8] | MINETER M J. A Software Framework to Create Vector-topology in Parallel GIS Operations[J]. International Journal of Geographical Information Science, 2003, 17(3): 203-222. |
| [9] | WU Hehai.Problem of Buffer Zone Construction in GIS[J]. Journalof Wuhan Technical University of Surveying and Mapping, 1997, 22(4):358-366. (毋河海. 关于GIS缓冲区的建立问题[J]. 武汉测绘科技大学学报, 1997, 22(4):358-366.) |
| [10] | ESRI. Buffer-GIS Dictionary[EB/OL].[2013-03-01].http://support.esri.com/en/knowledgebase/GISDictionary/term/buffer. |
| [11] | ZALIK B, ZADRAVEC M,CLAPWORTHY G. Construction of a Non-symmetric Geometric Buffer from a Set of Linesegments[J]. Computers & Geosciences,2003, 29(1):53-63. |
| [12] | BHATIAS, VIRAV, CHOKSI D, et al. An Algorithm for Generating Geometric Buffers for Vector Feature Layers[J]. Geo-spatial Information Science, 2013, 16(2): 130-138. |
| [13] | WU Huayi, GONG Jianya, LI Deren. Buffer Curve and Buffer Generation Algorithm in Aid of Edge-constrained Triangle Network[J].Acta Geodaetica et Cartograohica Sinica, 1999, 28(4):356-359. (吴华意, 龚健雅, 李德仁. 缓冲曲线和边约束三角网辅助的缓冲区生成算法[J]. 测绘学报, 1999, 28(4): 356-359.) |
| [14] | ZHU Huang, AI Tinghua, WANG Hong. The Buffer Construction of Line Object Based on the Geometric Scan Idea[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 171-176. (朱熀, 艾廷华, 王洪. 基于条带扫描思想的线目标缓冲区快速构建[J]. 测绘学报, 2006, 35(2): 171-176.) |
| [15] | LI Ke, DU Lin.An Algorithm of Buffer Zones Based on Algorithm of Dilation[J]. Journal of Institute of Surveying and Mapping, 2005, 22(3):229-231. (李科, 杜林. 基于膨胀算法的缓冲区分析的设计与实现[J]. 测绘学院学报, 2005, 22(3): 229-231.) |
| [16] | YAO Yiqiang, GAO Jinsong,MENG Lingkui, et al.Parallel Computing of Buffer Analysis Based on Grid Computing[J]. Geospatial Information, 2007, 5(1): 98-101. (姚艺强, 高劲松, 孟令奎, 等. 网格环境下缓冲区分析的并行计算[J]. 地理空间信息, 2007, 5(1): 98-101.) |
| [17] | VATTIB R. A Generic Solution to Polygon Clipping[J]. Communications of the ACM, 1992, 35(7): 56-63. |
| [18] | MURTA A. A Generic Polygon Clipping Library[EB/OL]. [2012-12-20].http://www.cs.man.ac.uk/-toby/alan/software/gpc.html. |
| [19] | GREINER G, HORMAN N K. Efficient Clipping of Arbitrary Polygons[J]. ACM Transactions on Graphics, 1998, 17(2): 71-83. |
| [20] | SUTHERLAND I E, HODGMAN G W. Reentrant Polygon Clipping[J]. Communications of the ACM,1974, 17(1):32-42. |
| [21] | WEILER K, ATHERTON P. Hidden Surface Removal Using Polygon Area Sorting[C] //Proceedings of the SIGGRAPH’77. New York: ACM Press, 1977:214-222. |
| [22] | GUTTMAN A. R-Trees: A Dynamic Index Structure for Spatial Searching[C] //Proceedings of ACM SIGMOD Conference on Management of Data. New York: ACM Press, 1984: 47-57. |


