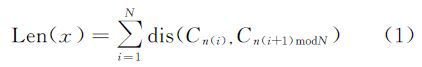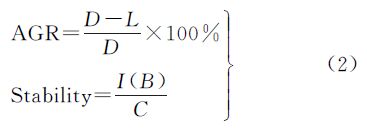2. 中国科学院大学,北京 100101;
3. 中国地质大学 信息工程学院,湖北 武汉 430074;
4. 地理信息工程国家重点实验室,陕西 西安 710054
2. University of Chinese Academy of Sciences, Beijing 100101, China;
3. Faculty of Information Engineering, China University of Geosciences, Wuhan 430074, China;
4. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China
交通网络旅行商路径优化问题(traveling salesman problem,TSP)旨在寻找由起点出发,有且仅有一次地通过给定点,再回到起点的成本最小的路径,它是最短路径算法应用的具体体现,也是主流GIS基础软件平台网络分析的重要功能之一[1, 2, 3]。TSP已经被证明是NP难题,多采用启发式算法求解,可分为构造型[4]和改进型[5]两类。构造型方法的基本思想是直接从距离矩阵中产生一个近似最优解,典型算法包括最近邻法、贪心法、插入法、Clarke-Wright算法等,该类方法实现简单、运行效率高,但对位置分布特殊的节点集求解质量很差。改进型方法的基本思想是不断改善给定的可行路径以寻找更优解,典型算法包括局部搜索算法和智能优化算法。其中,LKH算法[6]是目前精度最高的近似算法,但效率很低;遗传算法[7]具有较强的全局寻优能力,但进化后期收敛速度缓慢;模拟退火算法[8]具有渐进的收敛性,可依概率收敛到全局最优解,但对初始参数的设置较为敏感;禁忌搜索算法[9]具有较强的局部寻优能力,但对初始解和邻域结构的依赖性很强;蚁群算法[10]的结果不依赖于初始路径的选择,但因初期缺乏信息素限制了算法的收敛效率。
尽管目前对于小规模的TSP,精确型算法[11]已能够计算出全局最优解;而对于上百万的大规模TSP,启发式算法也能够快速获得近似最优解,但是这些算法并未考虑交通网络TSP的应用场景,大多使用欧氏距离计算最优回路。由于交通网络的TSP求解可能会考虑动态路况和交叉口耗费的影响,计算最优回路使用的是网路距离或出行时间,二者与欧氏距离之间不存在线性单调关系。因此,欧氏距离下的最优回路难以满足交通网络TSP路径规划需求。
综上所述,单一智能优化方法虽各有优势,但由于运算量过大,参数选择苛刻,对初值的依赖性强,很难快速实现全局优化。目前TSP研究的重点集中在结合多种优化机制和邻域搜索结构设计混合启发式算法[12, 13],以拓展算法的适用域、提高全局优化效果。此外,控制TSP算法的效率和精度的平衡,是目前TSP算法设计的核心难题。鉴于此,本文结合遗传算法良好的全局寻优能力和禁忌搜索独具特色的记忆功能来求解TSP,以期获得寻优能力强、运行效率高、结果稳定性好的TSP解决方案。
2 算法设计思想禁忌搜索(tabu search,TS)[14]是一种模拟人脑短期记忆功能的全局逐步寻优方法,它使用禁忌准则来避免无效的循环计算,同时采用藐视准则接受差解,以保证对不同范围有效路径的探测,具有较强的局部搜索能力。
遗传算法(genetic algorithm,GA)[15]是一种适用于求解大规模多目标函数全局优化问题的方法,可从解空间的多点出发进行自我学习式的广泛探索,具有很强的全局寻优能力。
在标准禁忌搜索算法[9]中,邻域的构造仅采用简单的移动操作,解之间高度的相似性削弱了算法跳出局部最优陷阱的能力,而遗传算法中的变异算子能产生具有新特性的个体,有效增加了路径组合的多样性,因此可以结合两种算法的优点设计混合型算法[16, 17]。此外,依概率发生的交叉和变异行为不能完全保证种群的持续性进化。因此,本文采用简化的遗传算法:直接进行变异来构建初始回路的邻域,再挑选出优秀个体进入局部搜索。
本文设计的TSP遗传禁忌搜索算法(genetic tabu search algorithm,GTSA)首先使用遗传变异算子作为分散策略构造邻域,使群体中的个体广泛地分布在解空间的大部分区域,保证算法的全局寻优能力;然后使用禁忌搜索作为集中策略进行局部的爬山优化,使个体不断突破已经到达过的局部最优解,避免早熟收敛。分散决策体现了群体智慧,有利于提高解空间的多样性;集中决策保证了全局执行力,有利于加大获得全局最优解的概率。同时,随着迭代次数的增加,分散决策逐步形成对集中决策的约束力量。在两者的相互作用中,内部竞争加剧,最终收敛到近似最优解。
GTSA的核心元素包括以下7个部分。
适应度函数:它是衡量一条回路质量优劣的标准,通常使用路径长度来评估个体的适应度。第x条路径的长度计算公式(1),dis(·)表示相邻两点间的距离,Cn(i)表示第i个点
邻域:变换初始回路中途经点的位置,产生的新回路集合称为初始回路的邻域。遗传算法的变异算子能增加解空间的多样性。为了改善禁忌搜索的邻域结构,扩大局部搜索的范围,本文依次使用交换、简单逆序、插入和移位变异算子[18]来构建初始回路的邻域。
移动:初始回路转移到它的邻域中的最优回路,称为一次移动。被采纳的移动即为下一次迭代过程的初始回路。
候选解集:初始回路的邻域子集。遗传算法的选择算子能引导算法朝着搜索空间中可能的最优区域进行探测。为了加快禁忌搜索的速度,本文使用了精英选择法,从初始回路的邻域中挑选出最优的10个回路构成候选解集,参与禁忌搜索。
禁忌表:一种存放禁忌对象的数据结构。一般情况下,禁忌表中的对象不能被选作为产生邻域的新解,以防止出现循环搜索和陷入局部最优解。
藐视准则:当候选解集中的最优对象比历史最优解还要好时,即使该对象被禁忌,仍可以替代历史最优解,作为下一次迭代过程的初始解,即特赦该禁忌对象。还有一种特赦情况是:若候选解集中的所有对象都被禁忌,则特赦最优候选解。
终止条件:算法达到预设的迭代次数,或者在固定周期内连续求得的最优解不变,二者满足其一即可终止计算过程,其中固定周期设置为算法迭代次数的0.6倍。
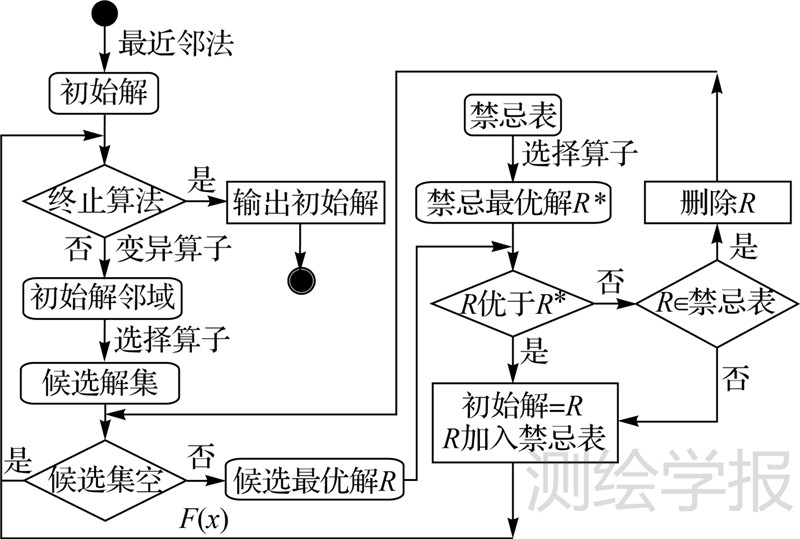
3 算法实现本文提出的TSP遗传禁忌搜索算法的具体实现过程如图 1所示。
|
| 图 1 TSP遗传禁忌搜索算法具体过程 Fig. 1 Genetic tabu search algorithm for TSP |
在搜索过程中可能会删除候选解集中的最优禁忌对象,因此候选解集不存在全部禁忌的状态。当候选解集为空时,继续在上一次的初始解附近搜索。该算法的时间复杂度为O(n2)。
4 试验与讨论 4.1 试验环境本文基于MapGIS二次开发平台实现了求解TSP的遗传禁忌搜索算法,并采用北京市二环以内的道路网络对算法进行了测试,网络包含1884个节点和2645条路段。试验中按随机采样的方法从网络中提取6组节点,数据规模依次为5、10、20、40、80、160,并将计算结果与禁忌搜索、遗传算法和ArcGIS软件的结果进行对比。测试环境如表 1所示。
| 硬件 | 软件 | ||||
| CPU | 内存 | 操作系统 | 开发环境 | 开发平台 | |
| Intel(R) Xeon(R) CPU E5520 | 4 GB | Microsoft Windows Server 2003 | Visual Studio 2005 | MapGIS K9 | |
本文采用解的精度增长率AGR(accuracy growth rate)、稳定性Stability和时间耗费Time Cost来评价算法的性能[19]。解的精度增长率计算公式中,D为ArcGIS得到的TSP路径长度,作为参考值;L为本文所涉及的3种算法得到的最优值。结果稳定性的计算公式中,C为同一组数据测试的总次数,默认值值为20;B为C次测试结果中的最优解,I为C次测试中得到B的次数。时间耗费是指算法的CPU耗时,单位为s
遗传算法和禁忌搜索均为启发式算法,故同一组数据的多次计算结果很难完全相同,使用式(2)时采用如下假设:当两次计算结果的AGR的差值小于1%时,认为两者相等。
4.3 参数设置根据现有算法的参数设置经验[7, 20],各参数取值如表 2所示,N为节点个数。
| 禁忌算法 | 遗传算法 |
|
|
| 40N | 24N | 10 | 2N | 40N | 24N | 0.8 | 0.05 |
当满足终止条件时,不同TSP算法的求解精度如表 3所示。当节点数在20以内时,3种算法的计算结果与参考值(ArcGIS的计算结果)相同;随着节点数的成倍增长,GTSA和GA算法的求解质量均优于参考值(平均提升了3%),比TS算法平均提升了9%。
| 算法 |
|
| TS | 0 | 0 | 0 | -1 | -7.6 | -9.7 |
| GA | 0 | 0 | 0 | 2.2 | 3.8 | 4.6 |
| GTSA | 0 | 0 | 0 | 2.2 | 4.4 | 5.1 |
由于TS的平均精度最低,因此以TS算法的计算精度为基准,分析3种算法的收敛性,表 4为3种算法收敛到指定精度的解时的计算次数。可见,同组数据中GTSA的收敛速度最快;随着数据规模的增大,GTSA快速收敛的优势愈加明显。当N=160时,GTSA的收敛速度是TS的6.8倍。当解值收敛到同一精度时,3种算法中计算次数的最大值小于3N。因此,可将迭代次数由40N改为3N,以减少计算冗余。
| N | AGR/(%) | TS | GA | GTSA |
| 5 | 0 | 1 | 1 | 1 |
| 10 | 0 | 37 | 3 | 1 |
| 20 | 0 | 18 | 6 | 2 |
| 40 | -1 | 50 | 4 | 3 |
| 80 | -8 | 226 | 8 | 5 |
| 160 | -10 | 82 | 15 | 12 |
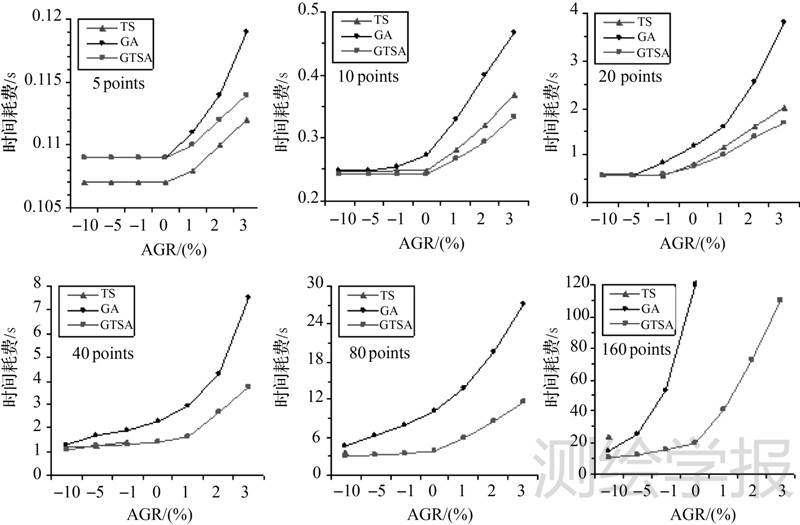
算法的精度和耗时关系曲线如图 2所示。试验结果表明,当精度增长率控制在[-10%,0]时,GTSA的平均收敛速度比GA快一倍;且随着精度的不断提升,GTSA的效率优势不断扩大。当解的质量优于参考值时,精度每提高一个百分点,耗时则成指数级增长,但GTSA的运行效率仍然领先。当节点数在20以内时,GTSA和TS算法的最大耗时之差仅为2%。然而,随着途经节点数的增加,TS算法首先失效,无法获得指定精度的解;而GA算法则随后出现无法在多项式时间内获得较参考值更优解的情况。
|
| 图 2 TSP算法精度—耗时曲线 Fig. 2 Curve of accuracy growth rate and time cost with three TSP algorithms |
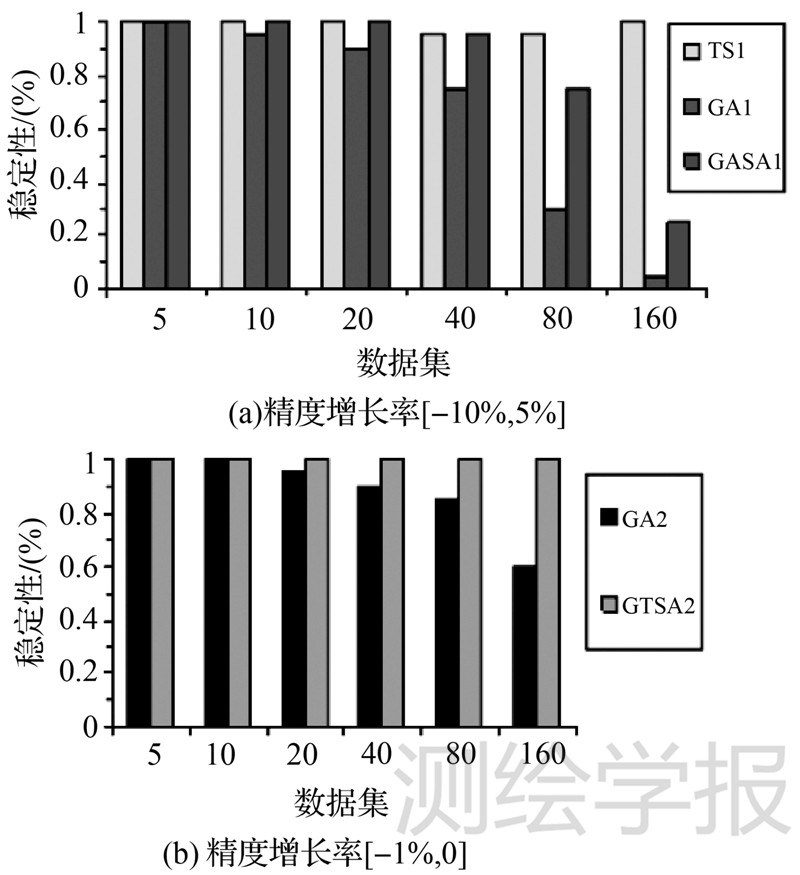
算法的稳定性试验结果如图 3(a)所示。其中GA1、TS1和GTSA1分别表示满足终止条件时算法的稳定性,此时GA和GTSA的AGR范围均为[0,5%],TS的AGR范围为[-10%,0]。可以看出,未对精度进行人工干预时,随着数据规模的逐步增大,GTSA和GA稳定性均急剧下降(GTSA的平均稳定度仅为0.83);而TS对于6组数据均保持着0.95以上的稳定度。
|
| 图 3 TSP算法的精度控制对稳定性的影响 Fig. 3 The influence of the accuracy on the stability with three TSP algorithms |
基于式(2)的假设,当算法的AGR在[-1%,1%]时,认为算法的计算结果与参考值相等。由于解的质量优于参考值时,GTSA和GA算法的耗时呈指数级增长;因此将算法的AGR控制在[-1%,0],以保证算法效率与精度的平衡。此时3种算法的稳定性如图 3(b)所示。结果显示,当前参数设置下的TS对于后3组数据已无法获得满足条件的可行解;而GTSA和GA的稳定性得到了显著提升,此时GTSA对于6组数据的稳定度均达到1,这说明在允许的误差范围内,一定的精度损失对于提高算法的稳定性具有积极的作用。
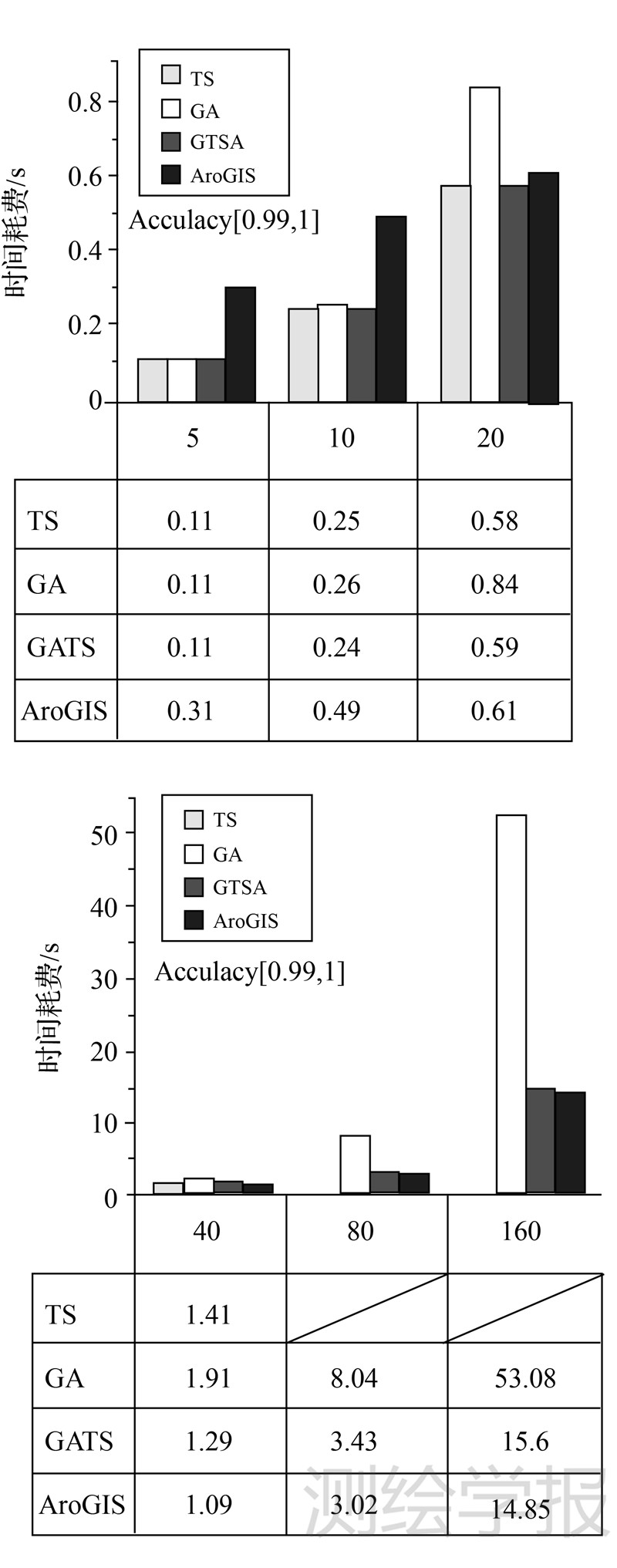
4.4.3 算法效率算法耗时和数据规模的关系(图 4)显示,随着节点数成倍增加,求解TSP的4种方法的耗时均呈指数级增长,其中GA增长最快;当途径节点数增加至40,TS算法失效,无法获得指定精度的解,详见图 3。当N=5时,GTSA与GA的耗时之比为1;而当N=160时该比值降为30%。前3组数据中,GTSA的运行效率略优于ArcGIS;而后3组数据中,GTSA的运行效率与ArcGIS持平。
|
| 图 4 精度误差1%以内时的算法效率 Fig. 4 Efficiency of three TSP algorithms when the precision error is less than 1% |
当解的精度误差控制在1%以内时,GTSA的稳定性和运行效率均优于TS和GA,并达到ArcGIS的水平。此时,GTSA对6组数据的TSP计算结果如图 5所示。
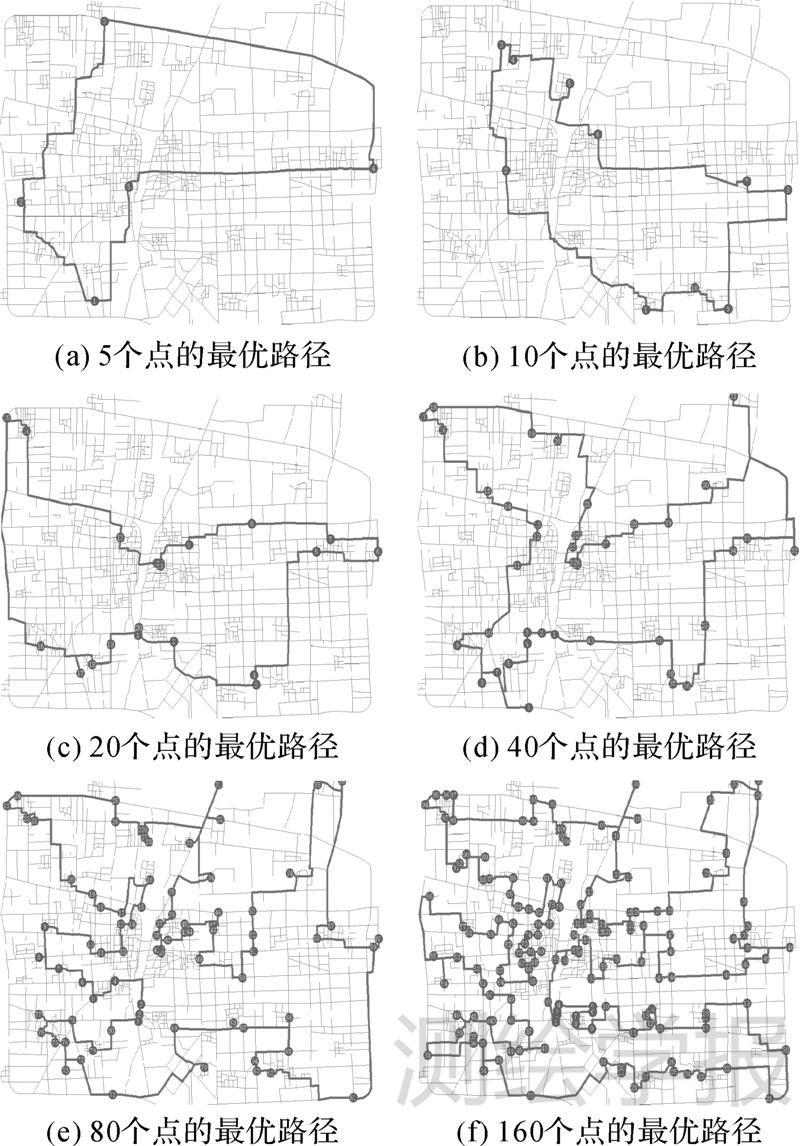
|
| 图 5 遗传禁忌搜索算法针对不同节点数求解TSP的结果(精度误差在1%以内) Fig. 5 Results of genetic tabu search algorithm when the precision error is less than 1% |
禁忌搜索算法的结果易受初始解和邻域结构的影响,但局部搜索能力强。遗传算法在进化后期收敛速度缓慢,但全局寻优效果好。两种算法结合后产生的遗传禁忌搜索算法整体性能明显优于两种单一的智能优化方法,可满足实际应用需求。此外,4种遗传变异算子构造邻域的过程是一个子任务之间相互独立的循环操作,它具有模块化和数据弱相关的特点,符合任务并行处理的机制。因此,可以考虑将遗传禁忌搜索算法进行并行化,以充分利用多核或集群的计算资源,最大限度地提升算法的运行效率。这是遗传禁忌搜索算法的一个潜在优势。遗传禁忌搜索算法的并行优化实现方法将在后续工作中展开深入研究。
同时,变异算子虽然增加了解空间的多样性,提升了算法获得全局最优解的概率,但是变异本身是盲目的,它无法保证遗传禁忌搜索算法以概率1收敛于全局最优解。后续工作中需要补充试验探讨不同的构建初始路径算法的特性,以及分析变异算子、邻域大小、禁忌长度等参数对算法性能的影响。
5 结 论本文设计了一种求解交通网络旅行商问题的遗传禁忌搜索算法。算法采用遗传变异算子作为分散策略构造邻域,使得解空间的多样性增强,能以更大的概率获得全局最优解;再使用禁忌搜索作为集中策略进行局部探测,加快了算法的后期收敛速度。与单纯的禁忌搜索和遗传算法相比,在求解精度相同的情况下,本文算法的鲁棒性更强,运行效率更高,稳定性更好。当解的精度损失控制在1%以内时,本文算法的运行效率已达到ArcGIS的水平。同时,遗传算法的并行特性使得本文算法的并行实现成为可能。在后续工作中,需要进一步研究如何使算法能够适应不同分布形态的节点集,以提高算法的普适性;同时需要研究如何对序贯算法进行并行化改造,以充分地利用计算资源,最大限度地提升算法的运行效率。
| [1] | LU Feng. Shortest Path Algorithms: Taxonomy and Advance in Research[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 269-275. (陆锋. 最短路径算法:分类体系与研究进展[J]. 测绘学报, 2001, 30(3): 269-275.) |
| [2] | YU Haicong, LU Feng. A Multi-modal Multi-criteria Route Planning Method Based on Genetic Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 89-96. (于海璁, 陆锋. 一种基于遗传算法的多模式多标准路径规划方法[J]. 测绘学报, 2014, 43(1): 89-96.) |
| [3] | LI Qingquan, LI Qiuping, FANG Zhixiang. An Emergency Evacuation Routing Optimization Method Based on Space-time Congestion Concept[J].Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 517-523. (李清泉, 李秋萍, 方志祥. 一种基于时空拥挤度的应急疏散路径优化方法[J]. 测绘学报, 2011, 40(4): 517-523.) |
| [4] | QI Yutao, LIU Fang, JIAO Licheng. Immune Algorithm with Self-adaptive Reduction for Large-scale TSP[J]. Journal of Software,2008, 9(16): 1265-1273. (戚玉涛, 刘芳, 焦李成. 求解大规模TSP问题的自适应归约免疫算法[J]. 软件学报, 2008, 9(16): 1265-1273.) |
| [5] | ZOU Peng, ZHOU Zhi, CHEN Guoliang, et al. A Multilevel Reduction Algorithm to TSP[J]. Journal of Software, 2003, 14(1): 35-42. (邹鹏, 周智, 陈国良, 等. 求解TSP问题的多级归约算法[J]. 软件学报, 2003, 14(1): 35-42.) |
| [6] | HELSGAUN K. An Effective Implementation of the Lin-Kernighan Traveling Salesman Heuristic[J]. European Journal of Operational Research, 2000, 126(1): 106-130. |
| [7] | XI Yugeng. Survey on Genetic Algorithm[J]. Control Theory and Applications, 1996, 13(6): 697-708. (席裕庚, 柴天佑, 恽为民. 遗传算法综述[J]. 控制理论与应用, 1996, 13(6): 697-708.) |
| [8] | KIRKPATRICK S, GELATT J C D, VECCHI M P. Optimization by Simulated Annealing[J]. Science, 1983, 220(4596): 671-680. |
| [9] | GLOVER F, KELLY J P, LAGUNA M. Genetic Algorithms and Tabu Search: Hybrids for Optimization[J]. Computers and Operations Research, 1995, 22(1): 111-134. |
| [10] | DAI Qiguo, JI Junzhong, LIU Chunnian. Knowledge-guiding Pheromone Control Strategy of Ant Colony Optimization[J]. Journal of Beijing University of Technology, 2011, 37(8): 1236-1241. (代启国, 冀俊忠, 刘椿年. 蚁群算法中基于知识引导的信息素控制策略[J]. 北京工业大学学报, 2011, 37(8): 1236-1241.) |
| [11] | SYLVIA B, GENEVIEVE L. Finding the Exact Integrality Gap for Small Traveling Salesman Problems[J]. Integer Programming and Combinatorial Optimization, 2002(2337): 83-92. |
| [12] | WANG Ling, ZHENG Dazhong. Meta-heuristic Algorithms: a Review[J]. Control and Decision, 2000, 15(3): 257-262. (王凌, 郑大钟. Meta-heuristic算法研究进展[J]. 控制与决策, 2000, 15(3): 257-262.) |
| [13] | THAMILSELVAN R, BALASUBRAMANIE P. A Genetic Algorithm with a Tabu Search for Traveling Salesman Problem[J]. International Journal of Recent Trends in Engineering, 2009, 1(1): 607-610. |
| [14] | FRED G. Future Paths for Integer Programming and Links to Artificial Intelligence[J]. Computers and Operations Research, 1986, 13(5): 533-549. |
| [15] | GREFENSTETTE J J, GOPAL R, ROSMAITA B, et al. Genetic Algorithm for TSP[C]//Proceedings of the First International Conference on Genetic Algorithms of the First International Conference on Genetic Algorithms and Their Applications. Pittsburg: Psychology Press, 1985: 160-168. |
| [16] | YANG N, TIAN W F, JIN Z H. Crossover Tabu Search for Traveling Salesman Problem[J]. Journal of System Simulation, 2006, 18(4): 897-908. |
| [17] | KE Ke, ZHANG Shiying. Research on the Tabu Hierarchy Genetic Algorithm[J]. Control and Decision, 2001, 16(4): 480-483. (柯珂, 张世英. 禁忌-递阶遗传算法研究[J]. 控制与决策, 2001, 16(4): 480-483.) |
| [18] | LIU Jun, WANG Jiesheng. Solving Traveling Salesman Problem(TSP) with Pseudo Parallel Genetic Algorithms[J].Control Theory and Applications, 2007,24(2): 279-282. (刘军, 王介生. 旅行商问题(TSP)的伪并行遗传算法[J]. 控制理论与应用, 2007,24(2): 279-282.) |
| [19] | GAO Song, LU Feng. The Kth Shortest Path Algorithms: Accuracy and Efficiency Evaluation[J]. Journal of Image and Graphics, 2009,14(8): 1677-1683. (高松, 陆锋. K则最短路径算法效率与精度评估[J]. 中国图象图形学报, 2009,14(8): 1677-1683.) |
| [20] | SEXTONA R S, ALIDAEEB B, DORSEY R E, et al. Global Optimization for Artificial Neural Networks: A Tabu Search Application[J]. European Journal of Operational Research, 1998, 106(2): 570-584. |