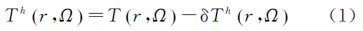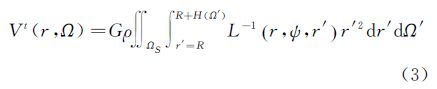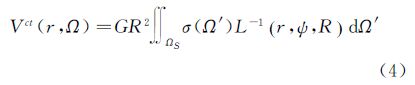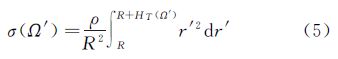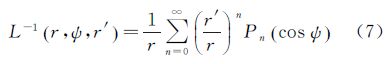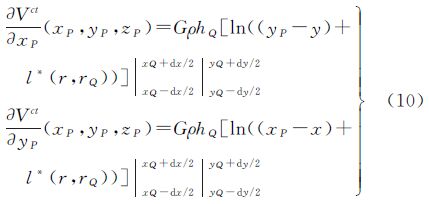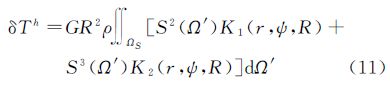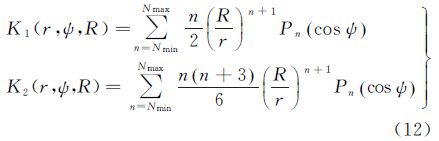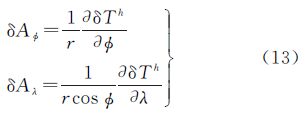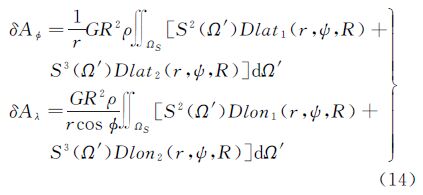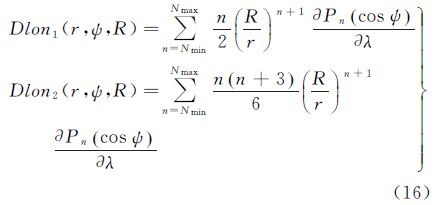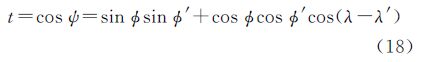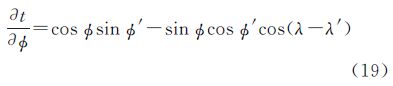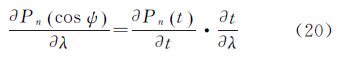2. 武汉大学 测绘学院, 湖北 武汉430079；3. 武汉大学 地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079,China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079,China
地形起伏反映了地球重力场的不规则变化，精确确定地形对地球重力场的影响具有十分重要的意义[1, 2, 3]。第二类Helmert凝集法是目前应用最为广泛的地形归算方法，其基本思想是将大地水准面外部地形质量引力位与凝集层地形质量引力位作差得到地形对引力位的直接影响，再转化为地形对重力的直接影响，从而将重力观测值转化至Helmert调和空间，求解大地测量边值问题得到调整大地水准面(co-geoid)后再恢复地形位和凝集层位产生的间接影响即可计算出真实的大地水准面[4, 5]。第二类Helmert凝集法分为解析形式和级数展开形式，前者提供全波段的地形质量改正，后者则是将牛顿积分核函数展开成Legendre多项式的收敛级数，可用来计算带限地形影响。
航空重力测量是在动态环境中进行的，各类观测数据中包含了大量的高频观测噪声，消除这些噪声的主要手段是使用低通滤波器，滤波后得到的重力信号为带限重力信号[6, 7, 8, 9]。因此，采用解析公式计算的全频谱地形直接影响和间接影响对航空矢量重力观测值进行改正是不合理的，解决这一问题的方法有两类：①将地形改正值也作相应的低通滤波处理，使得地形效应的频谱范围与航空重力观测值一致[10]，这种解决方案需要输入飞行高度上密集采样点处的地形质量影响值，采用高分辨率的DEM来进行计算时工作量相当庞大；②基于第二类Helmert凝集法的级数形式，采用带限公式来计算地形质量对引力位和重力扰动的直接影响公式和大地水准面的间接影响[11, 12, 13]，这种解决方法的优点是可依据重力观测值的频谱范围来调整积分核函数的起始阶数和最高阶数，从而避免对地形质量影响作低通滤波处理，原理简单而且计算方便。文献[11]基于第二类Helmert凝集法的级数形式推导出地形质量对引力位和重力扰动的带限直接影响改正公式以及对大地水准面的带限间接影响改正公式，将基于级数核计算的带限直接地形影响和间接地形影响与基于解析核计算并经低通滤波处理后得到的带限直接地形影响和间接地形影响进行了比较，验证了算法的有效性，这一套带限地形影响改正公式可对重力扰动或重力异常进行地形归算，针对的是航空标量重力测量观测值。航空重力矢量测量获取的是扰动重力的3个分量，而针对水平分量带限地形影响改正的研究尚未有公开的文献发表。本文在文献[11]的研究基础上，推导出重力水平分量的带限直接地形影响改正公式，并通过数值计算与分析来验证该算法的有效性。
2 第二类Helmert凝集法Helmert调和空间内某点的扰动位Th(r,Ω)与真实地球扰动位T(r,Ω)具有以下关系
式中,r为计算点到地心的距离;δTh(r,Ω)为地形对引力位的直接影响，是大地水准面外地形的引力位与凝集层地形引力位之差 式中,Vt为大地水准面外的地形引力位;Vct为凝集层地形引力位，分别可表示为 式中,G为万有引力常数；R为地球平均半径，取为6 371 000 m；ρ为地壳平均密度，取为2.67 g/cm3；r′为流动点到地心的距离；ΩS表示积分区域；HT(Ω′)为流动点的地形高度；dΩ′=cos ø′dø′dλ′为积分元；σ(Ω′)为凝集层面密度，因大地水准面外地形质量与凝集层质量相等，σ(Ω′)可写为[14] L－1为牛顿积分核函数，其解析形式如下 当r>r′时，式(6)还可展开为Legendre多项式的收敛级数 式中,ψ为计算点Ω=(ø,λ)和流动点Ω′=(ø′,λ′)之间的球面距离。 3 重力水平分量的全频谱地形影响
文献[15]给出了平面逼近下大地水准面外地形对重力水平分量的影响
式中,s=x,y；P为计算点;Q为流动点;x轴正方向为东向;y轴正方向为北向。式(8)可以化为卷积形式，并通过快速傅里叶FFT来计算[16]。
平面逼近下凝集层地形对引力位的影响为[15]
式中,κ(Q)=hQρ;l*(r,rQ)=
;z*为积分元几何中心的垂直坐标；hQ为Q点的地形高。式(9)对xP、yP分别求导可得凝集层地形对重力水平分量的影响
4 引力位的带限直接地形影响
文献[11]给出了引力位的带限直接地形影响的计算公式
式中,Sk(Ω′)=
；K1和K2为积分核函数，其具体定义如下
式中,Pn (cos ψ)为第n阶Legendre多项式；Nmin为起始阶数，Nmax为最大阶数，这意味着可以通过改变Nmin和Nmax的大小来使地形影响的频谱范围与重力观测值保持一致。若求解边值问题时采用移去-恢复法，则Nmin－1应为所选取参考位模型的最大阶数。
5 重力矢量水平分量的带限直接地形影响
依据重力矢量各分量与扰动位的关系[17]，对式(11)作如下变换即可得重力北向分量和东向分量的带限地形影响
式(11)中仅Pn (cos ψ)与ø及λ有关，则式(13)可写为 式中,Dlat1、Dlat2、Dlon1、Dlon2为积分核函数 令t=cos ψ，则按复合函数的求导法则，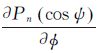
可写为
多项式Pn (t)与其一阶导数
的计算见文献[18]，而t为计算点与流动点的地心纬度和经度的函数，其表达式为
式(18)对ø求偏导，得
同理可得
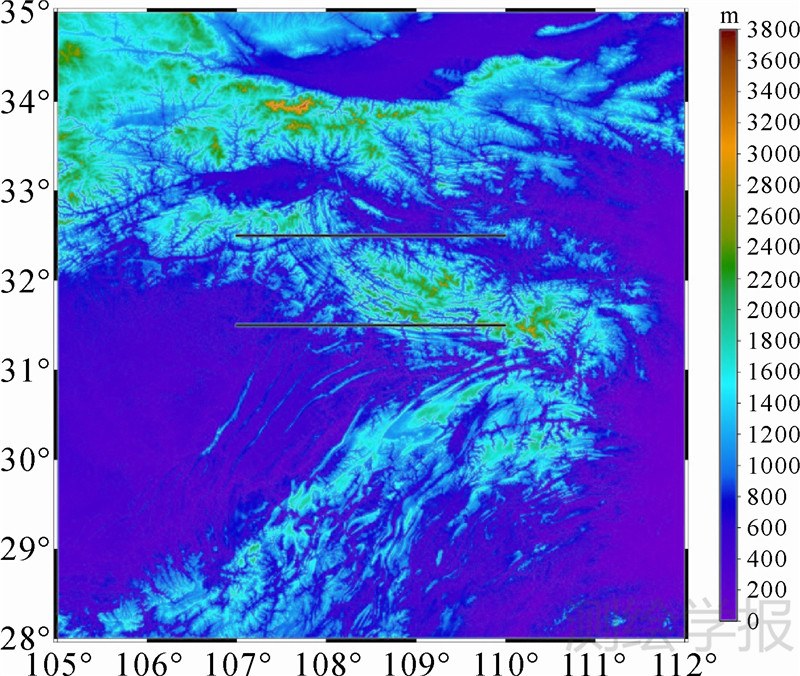
6 数值计算与分析
为验证在第二类Helmert凝集法框架下导出的重力水平分量带限直接地形影响的计算模型，本文采用SRTM(shuttle radar topography mission)[19]地形高程数据分别计算了重力水平分量的带限直接地形影响和全频谱直接地形影响，并进行比较检校。所选数据点区域由纬线[28°N，35°N]和经线[105°E，112°E]围成，位于中国西部，图 1为该区域的实际地形。
|
| 图 1 SRTM地形 Fig. 1 SRTM topography |
选取两条沿纬圈方向的航线，纬度分别为31.5°N和32.5°N，经度范围为[107°E，110°E](图 1)，图 2给出了这两条纬线的地形高程剖面。分别依据式(14)计算了两条纬线上重力矢量水平分量的带限直接地形影响(飞行高度为4 km)，积分核式(15)、式(16)的起止阶数分别取为Nmin=0和Nmax=2160，对应重力观测值的分辨率为5′×5′，同时基于解析牛顿积分核计算了相应点位处重力水平分量的全频谱直接地形影响。图 3—图 6分别给出了在4 km飞行高度处沿上述两条纬线的重力北向水平面分量和东向水平分量的直接地形影响，其中左图是基于0~2160阶级数展开核的带限直接地形影响与基于解析核的全频谱直接地形影响的比较，右图为基于级数展开核计算的带限直接地形影响与基于解析核并经低通滤波处理后所得直接地形影响的比较，低通滤波器采用文献[20]中介绍的迭代高斯滤波，滤波窗口选为5′。
|
| 图 2 沿纬线31.5°和32.5°的地形高度剖面 Fig. 2 Topography height profiles along the parallels of 31.5°N and 32.5°N |
|
| 图 3 沿31.5°N纬线4 km飞行高度处北向分量的直接地形影响 Fig. 3 DTE for northern component at 4 km flight height along the parallel of 31.5°N |
|
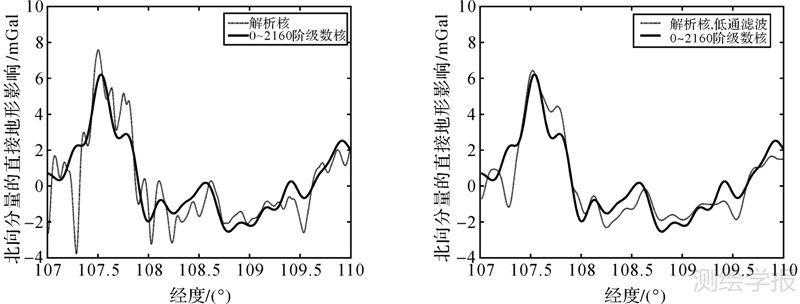
| 图 4 沿32.5°N纬线4 km飞行高度处北向分量的直接地形影响 Fig. 4 DTE for northern component at 4 km flight height along the parallel of 32.5°N |
|
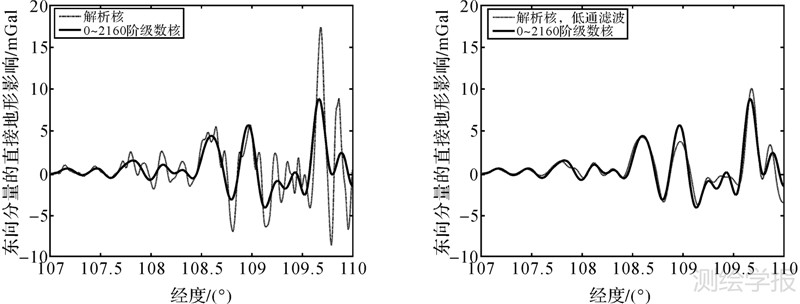
| 图 5 沿31.5°N纬线4 km飞行高度处东向分量的直接地形影响 Fig. 5 DTE for eastern component at 4 km flight height along the parallel of 31.5°N |
|
| 图 6 沿32.5°N纬线4 km飞行高度处东向分量的直接地形影响 Fig. 6 DTE for eastern component at 4 km flight height along the parallel of 32.5°N |
从图 3—图 6中可以看出，按照式(14)计算的重力水平分量的带限直接地形影响与基于解析牛顿核计算的全频谱直接地形影响在整体趋势上比较吻合，区别在于前者更为平滑，而后者则表现出更多的高频特性，这是由二者的频谱范围决定的，前者最大频谱对应的是2160阶，而后者代表的是全频谱的地形质量影响。对全频谱地形影响进行低通滤波处理使其与带限地形影响频谱范围一致之后，两者的吻合程度大幅提高，但二者之间仍存在一定的差异，这是因为低通滤波技术并不能滤掉截止频率之外的所有的高频信号。表 1列出了低通滤波前后基于级数展开牛顿核的地形影响与基于牛顿解析核的地形影响的差值统计信息，滤波后二者之差的最大值、最小值大幅减小，RMS也降至实测航空重力数据的精度范围之内，说明由基于级数展开核计算的带限直接地形影响可用于航空矢量重力测量水平分量观测值的地形归算。
| 北向分量 | 东向分量 | ||||||||
| 最小值 | 最大值 | 平均值 | RMS | 最小值 | 最大值 | 平均值 | RMS | ||
| 31.5°纬线 | -6.20 | 6.01 | -0.67 | 2.09 | -9.14 | 8.53 | -0.03 | 2.30 | |
| 31.5°纬线，低通滤波 | -3.63 | 4.34 | -0.65 | 1.52 | -1.81 | 2.79 | -0.02 | 0.82 | |
| 32.5°纬线 | -2.34 | 6.01 | 0.15 | 1.19 | -3.97 | 4.29 | 0.03 | 1.25 | |
| 32.5°纬线，低通滤波 | -1.61 | 3.37 | 0.14 | 0.87 | -2.26 | 3.60 | 0.02 | 0.75 | |
值得注意的是，重力水平分量的带限地形影响计算公式也有一定的局限性，当航空矢量重力测量的分辨率提高，如由本文中的5′×5′提升至1′×1′时，Nmax的值由2160增加至10 800，计算量将会大幅增加。
7 结 论航空矢量重力测量的水平分量观测值是带限重力信号，本文从第二类Helmert凝集法的基本原理出发，推导出适用于航空重力矢量测量水平分量带限地形影响的改正公式，该公式可通过调节核函数的起始阶数和最大阶数来使水平分量的地形影响具有与水平分量一致的频谱范围。
| [1] | LUO Zhicai, CHEN Yongqi, NING Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3), 340-344. (罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报:信息科学版, 2003, 28(3):340-344.) |
| [2] | BAJRACHARYA S. Terrain Effects on Geoid Determination[R].Calgary:University of Calgary, 2003. |
| [3] | JEKELI C, SERPAS J G. Review and Numerical Assessment of the Direct Topographical Reduction in Geoid Determination[J]. Journal of Geodesy, 2003, 77(3-4): 226-239. |
| [4] | SERPAS J G, JEKELI C. Local Geoid Determination from Airborne Vector Gravimetry[J]. Journal of Geodesy, 2005, 78(10): 577-587. |
| [5] | WANG Y M. Precise Computation of the Direct and Indirect Topographic Effects of Helmert’s 2nd Method of Condensation Using SRTM30 Digital Elevation Model[J]. Journal of Geodetic Science, 2011, 1(4): 305-313. |
| [6] | NOVÁK P, KERN M, SCHWARZ K P. Numerical Studies on the Harmonic Downward Continuation of Band-limited Airborne Gravity[J]. Studia Geophysica et Geodaetica, 2001, 45: 327-345. |
| [7] | NOVÁK P,HECK B. Downward Continuation and Geoid Determination Based on Band-limited Airborne Gravity Data[J]. Journal of Geodesy, 2002, 76(5): 269-278. |
| [8] | NOVÁK P. Optimal Model for Geoid Determination from Airborne Gravity[J]. Studia Geophysica et Geodaetica, 2003, 47: 1-36. |
| [9] | NOVÁK P, KERN M, SCHWARZ K P, et al. On Geoid Determination from Airborne Gravity[J]. Journal of Geodesy, 2003, 76(9): 510-522. |
| [10] | BAYOUD F A, SIDERIS M G. Two Different Methodologies for Geoid Determination from Ground and Airborne Gravity Data[J]. Geophysics, 2003, 71(6): 171-180. |
| [11] | NOVÁK P, KERN M, SCHWARZ K P, et al. Evaluation of Band-limited Topographical Effects in Airborne Gravimetry[J]. Journal of Geodesy, 2003, 76(11): 597-604. |
| [12] | HÁJKOVÁ J. Local Geoid Determination Based on Airborne Gravity Data[J]. Studia Geophysica et Geodaetica, 2011, 55: 515-528. |
| [13] | JIANG Tao. Regional Geoid Determination Using Airborne Gravimetry Data[J]. Acta Geodaetica et Cartographica Sinica,2013,42(4):152.(蒋涛. 利用航空重力测量数据确定区域大地水准面[J]. 测绘学报,2013,42(4):152.) |
| [14] | WICHIENCHAROEN C. The Indirect Effects on the Computation of Geoid Undulations[R]. Columbus: Ohio State University, 1982. |
| [15] | MAKHLOOF A A E. The Use of Topographic-isostatic Mass Information in Geodetic Applications [R]. Bonn: Institut of Geodesy and Geoinformation, 2008. |
| [16] | LI Y C, SIDERIS M G, SCHWARZ K P. Unified Terrain Correction Formulas for Vector Gravity Measurements[C]//Proceedings of Indian National Science Academy Part A. Hyderabad: [s.n.],2000: 521-536. |
| [17] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman, 1967. |
| [18] | KOOP R. Global Gravity Field Modelling Using Satellite Gravity Gradiometry[M]. Amersfoort:Nederlandse Commissie voor Geodesie, 1993. |
| [19] | FARR T G, ROSEN P A, CARO E, et al. The Shuttle Radar Topography Mission[J]. Reviews of Geophysics, 2007, 45(2):111-116. |
| [20] | HWANG C, HSIAO Y S, SHIH H C. Data Reduction in Scalar Airborne Gravimetry: Theory, Software and Case Study in Taiwan[J]. Computers and Geosciences, 2006, 32: 1573-1584. |