车辆路径问题(vehicle routing problem,VRP)是对车辆的运行线路进行合理规划与优化,在满足各种约束条件的情况下,使车辆以最小的费用通过所有装货点或卸货点[1]。获取VRP问题的最优解具有重要的实用价值,能有效降低物流运输的成本。因此,VRP问题一直是运筹学、GIS网络分析研究中的热点问题之一。VRP是一个经典的NP(non-deterministic polynomial)问题,无法在多项式时间内获取精确解,且随着客户点数的增加,可选车辆路径方案数量和求解时间均呈几何级数式增长[2]。随着实际应用中VRP规模的不断扩大,传统的串行算法已无法满足大规模地理网络VRP问题的求解需要。
而并行技术能够充分利用多核、多CPU、GPU、PC集群、大规模并行计算机等提供的高性能计算能力,大幅提高地理运算的效率[3, 4, 5, 6]。国内外学者应用不同的并行策略对VRP算法进行了深入的研究。文献[7, 8]基于迭代局部搜索框架和禁忌搜索算法,设计了并行VRP算法;文献[9]应用客户点集分割的策略,发展了一种结合局部搜索与整数规划的并行算法;文献[10]将多种不同的邻域结构融入禁忌搜索过程,提出多邻域协作并行VRP算法;文献[11]设计了自适应大邻域局部搜索算法;文献[12]提出了基于双禁忌对象的并行禁忌搜索算法。但上述并行VRP算法多以大规模并行服务器(计算节点数>128)为基础,针对基于PC集群的并行VRP算法研究较少。PC集群成本低廉,易于搭建与维护,是应用最为广泛的并行算法运行平台。但与大规模并行硬件环境相比,PC集群存在着计算节点内存小、通信速度慢等问题。为此,本文拟以PC集群环境为基础,设计分布式数据存储结构,以降低算法对内存的需求量,并采用邻域分解策略实现VRP算法的并行化,通过精简通信数据结构降低计算节点间的通信开销,进而提高PC集群环境中求解大规模地理网络VRP问题的效率。
2 并行地理网络VRP算法
2.1 地理网络VRP算法流程
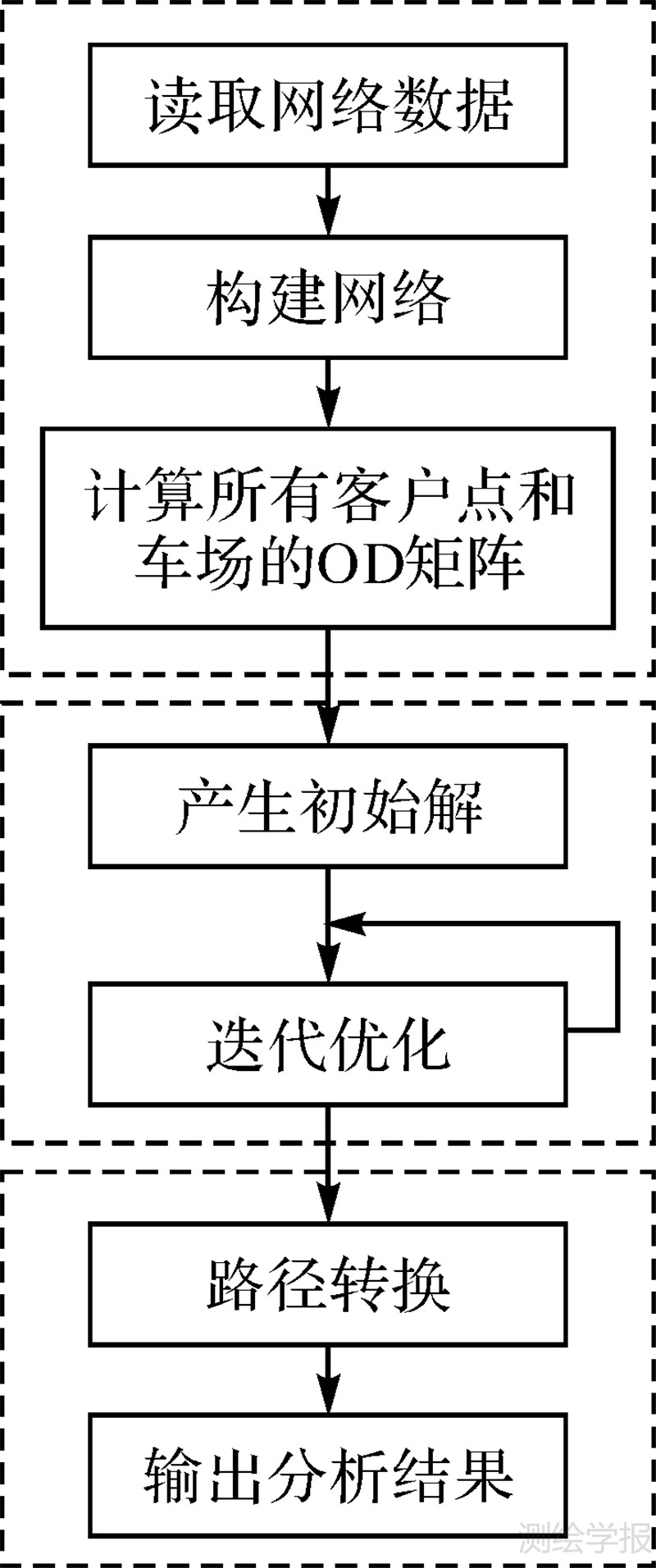
求解VRP时,需要反复用到网络节点(包括客户点和车场点)中任意两点间的距离。图论中,网络节点间的距离多采用欧氏距离[13],见图 1(a),计算简单快捷,无须设计相应的矩阵进行存储。而地理网络中,网络节点间距离多采用节点间最短路径的距离值,见图 1(b)。由于最短路径求解用时远多于欧氏距离的计算耗时,因此,地理网络VRP求解过程中需建立网络节点间的距离矩阵,即origin-destination(OD)矩阵。随着地理网络规模的扩大,OD矩阵所需存储空间将呈指数形式增长,从而导致PC集群各计算节点出现内存不足的问题。因此,需采用分布式存储结构,以减少OD矩阵对内存的占用量。在获取OD矩阵的基础上,应用随机法产生初始解,采用邻域分解策略对VRP迭代优化过程进行并行化,以获取客户点序号编码,即VRP问题的解。最后,为了获取实际的运输路径,需将客户点序号编码转换为车辆的实际运送路径。地理网络VRP问题的求解流程如图 2所示。

|
| 图 1 VRP中的距离值 Fig. 1 Distance in VRP |
|
| 图 2 地理网络VRP求解流程 Fig. 2 Procedure of solving VRP in geographical network |
OD矩阵包括距离矩阵D和前趋矩阵P两部分:前者记录了任意两节点间的最短距离;后者记录了任意两节点间的最短路径。它们均是地理网络VRP求解的基础。假设c为客户点数,w为车场数,n为网络节点数,则矩阵D的大小为(c+w)×(c+w),矩阵P的大小为(c+w)×n。通常网络节点数n远大于c,因此P远大于D。以网络节点数n=200 000,客户点数c=3000,车场数w=1的VRP问题为例,假设每个矩阵元素占4 Byte,OD矩阵将占用大约2.4 GB的内存空间。若不对OD矩阵的存储方式进行优化处理,很容易出现各计算节点内存不足的问题。此外,OD矩阵的计算也是VRP求解过程中耗时最多的环节。笔者利用ArcGIS提供的VRP分析工具,使用试验数据(网络节点数为100 703个,边数为124 164条,车场个数为1,客户点数为1000个,车辆数为10辆)测试了OD矩阵计算用时占算法整体时间的比重。结果表明:OD矩阵计算耗时占VRP算法总用时的65%,是VRP算法中耗时最多的环节之一。因此,降低OD矩阵的存储开销、减少OD矩阵的计算用时对保证VRP算法的稳健性和高效性具有重要意义。
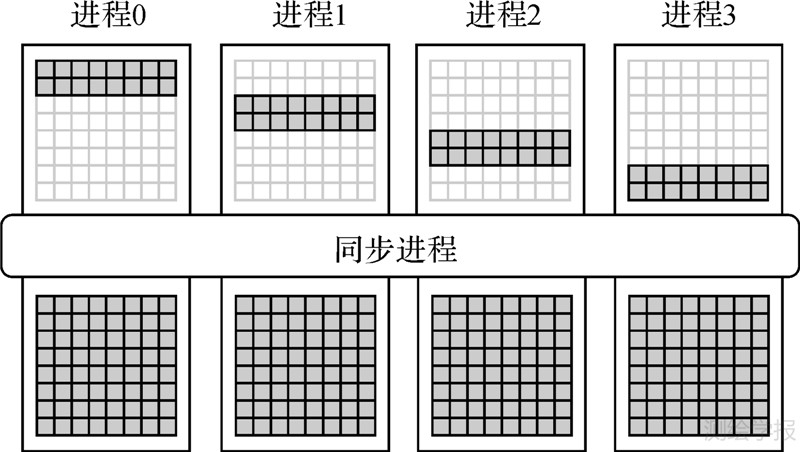
为了降低OD矩阵的内存开销,本文采用了分布式存储的策略。矩阵D占用内存空间较小,且为后续禁忌搜索过程的基础,因此各进程均存储完整的D;而矩阵P十分庞大,且仅用于后续的路径转换过程,因而将其分布式存储于各进程中。通过这种策略,单进程内存开销近似减少为原来的1/p(p为进程数)。同时,为了提高OD矩阵的计算效率,引入并行Johnson算法来获取各客户点及车场点间的最短路径。具体实现过程如下:首先,将c+w个源点(包括客户点和车场点)平均分配至p个进程,每个进程分别计算(c+w)/p个源点的最短路径,得到部分D和P;然后,应用讯息传递接口(message passing interface,MPI)中的Allgather函数对D进行同步操作,使得各进程均获得完整的矩阵D,如图 3所示(以4进程为例)。通过分布式存储策略和并行Johnson算法,OD矩阵计算过程的时间复杂度降低为O(cn logn/p),空间复杂度降低为O(cn/p)。由此可以看出,随着进程数的增加,该算法能够处理更大规模的OD矩阵,具有很强的扩展性。
|
| 图 3 DM矩阵的同步方法 Fig. 3 Synchronizing of distance matrix |
VRP问题无法在多项式时间内获得精确解,因此多采用启发式算法来求解[14]。禁忌搜索算法是一种常用的启发式算法,是解决组合优化问题行之有效的方法[15]。该算法采用一定的藐视准则使搜索过程跳出局部最优解,从而提高了获得全局最优解的可能性[16]。国内外大量研究成果表明,禁忌搜索算法是解决VRP问题的有效途径,具有求解效率高、解质量稳定等优点[17, 18, 19, 20, 21, 22, 23]。因此,本文拟对串行禁忌搜索算法进行并行化,来完成VRP问题的求解。
禁忌搜索算法的实现流程如图 4所示。首先,采用随机法(辅以最低成本增加法)构建若干初始解,选取目标函数值最小的解作为当前解S和最优解S*。然后利用迭代邻域搜索对最优解进行优化,具体过程如下:①利用随机交换法和插入法得到S的邻域;②从邻域中搜索目标函数值最小的解S′,判断其是否满足特赦准则,若满足则用该解更新最优解S*,否则判断其禁忌属性,若未被禁忌则用该解更新当前解S,否则继续搜索邻域中其他解;③更新禁忌表,判断是否满足终止条件。当该迭代过程达到终止条件后,即得到最终解S*。从禁忌搜索算法的实现过程可以看出,由于禁忌准则的使用,各次迭代间具有内在的关联性。若采用任务划分的方式进行并行化,会破坏禁忌搜索机制,从而影响最终的求解质量。因此,本文采用细粒度的并行方式,对邻域搜索过程进行并行化。具体实现过程如下:首先,将待搜索邻域中的N个邻解平均分配至p个进程,各进程分别搜索N/p个邻域解得到局部最优解;然后,由主进程回收各进程的局部最优解,比较得到全局最优解后再广播给各进程;最后,各进程根据邻域搜索获得的最优解更新当前解、最优解和禁忌表。在解的迭代优化过程中,邻域搜索过程耗时最多,通过对该过程的并行化可以有效提高禁忌搜索的效率。

|
| 图 4 禁忌搜索算法流程 Fig. 4 Flow chart of tabu search |
在并行邻域搜索过程中,各进程需要频繁地进行数据交换。若采用发送解编码的方式进行同步,一次迭代中的通信量将达到2s个整型值(s为解编码长度,约等于客户点数),会产生大量的通信开销。为此,本文引入一种新的通信模式。为了减少通信量,采用发送解编码变换规则的方式,无须发送完整的解编码。与解编码相比,编码变换规则的长度仅为8个整型,大幅降低了通信量,提高了进程间的通信效率。具体实现步骤如下:①各从进程发送局部最优解的目标函数值至主进程(通信量为1个整型);②主进程进行比较后得到全局最优值,并将该值对应的解所在进程编号广播给各进程(通信量为1个整型);③由包含最优解的进程向其他各进程广播最优解的编码变换规则(通信量为8个整型)。由此过程可以看出,每次邻域搜索的通信量为10个整型数据。解编码变换规则可用向量T(含8个整型)表示
为了验证算法的有效性和正确性,本文利用模拟的路网数据进行了相关试验。试验环境为两台双核计算机(CPU为Intel Core i3-530,内存为3.24 GB)和一台四核计算机(CPU为Intel Core i5-2400,内存为3.24 GB)组成的Windows PC集群,最多可运行8个进程。消息传递接口采用MPICH2。试验数据为6个人工生成的测试数据集,如表 1所示。试验均将车辆数(等价于距离约束)和每辆车的容量设为约束条件,以配送路径长度总和为目标函数值。客户点和车场点均从网络节点中随机选取。
| 数据集编号 | 网络规模 | VRP规模 | ||||
| 点数 | 边数 | 客户点数 | 车辆数约束 | 容量约束 | ||
| 1 | 100 703 | 124 164 | 1000 | 10 | 2100 | |
| 2 | 100 703 | 124 164 | 2000 | 20 | ||
| 3 | 100 703 | 124 164 | 3000 | 30 | ||
| 4 | 203 152 | 251 272 | 1000 | 10 | ||
| 5 | 203 152 | 251 272 | 2000 | 20 | ||
| 6 | 203 152 | 251 272 | 3000 | 30 | ||
为了验证VRP并行策略的可行性,分别统计了串行VRP算法中各计算环节的耗时情况。由于禁忌搜索算法是启发式算法,每次的运行结果略有不同,取10次运行结果的平均值作为最终结果。测试结果如表 2和图 5所示。其中,OD项表示OD矩阵计算时间;TS项表示禁忌搜索时间;其他项表示数据读取、预处理等过程所消耗的时间。
| 数据集 | 总时间/s | OD/s | OD/总时间/(%) | TS/s | TS/总时间/(%) | (OD+TS)/总时间/(%) | 其他/s |
| 1 | 71.94 | 28.59 | 39.7 | 40.39 | 56.1 | 95.8 | 2.96 |
| 2 | 255.40 | 56.35 | 22.1 | 196.01 | 76.7 | 98.8 | 3.05 |
| 3 | 603.61 | 84.84 | 14.1 | 515.81 | 85.4 | 99.5 | 2.96 |
| 4 | 102.54 | 61.49 | 60.0 | 30.92 | 30.2 | 90.2 | 10.14 |
| 5 | 313.22 | 123.37 | 39.4 | 179.08 | 57.2 | 96.6 | 10.77 |
| 6 | — | — | — | — | — | — | — |

|
| 图 5 串行VRP算法各部分耗时比重 Fig. 5 Time consumption of each procedure in serial VRP algorithm |
表 2中,采用单进程进行VRP求解时,由于计算过程均放在一个计算节点内执行,未进行数据的分布式存储,导致测试数据集6出现内存不足的问题,无法求出最终结果。其他测试结果表明,OD计算耗时占算法总用时的比重在14.1%~60.0%之间,TS计算过程用时占算法总用时的比重在30.2%~85.4%之间;OD矩阵计算和TS过程用时总和占算法总用时的比重在90.2%~99.5%之间。因此,对VRP算法中的OD矩阵计算和TS搜索过程进行并行化,能有效提高VRP算法的整体性能。
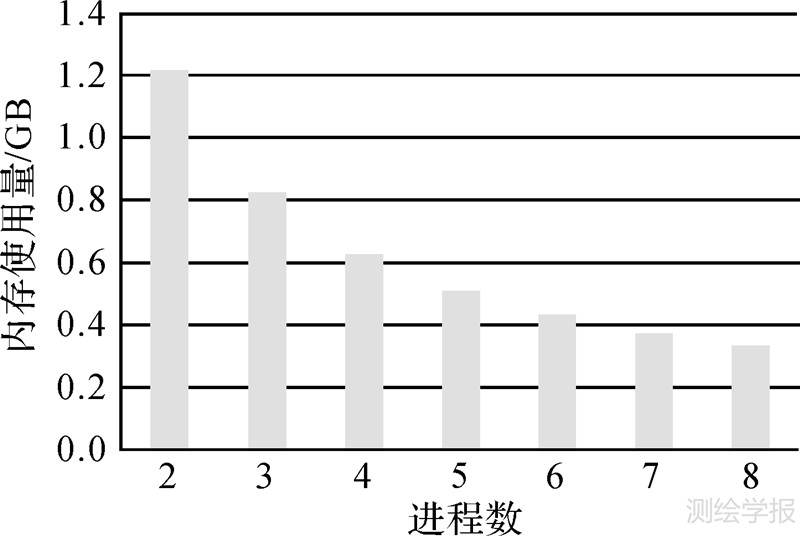
3.3 OD矩阵计算的存储开销及并行效率分析为了进一步分析分布式存储策略对内存使用的影响,以测试数据6为例,分别测试了采用不同进程数时OD矩阵计算过程的内存消耗情况。采用单进程时,由于无法发挥分布式存储策略的作用,VRP求解过程中出现了内存不足的现象。因此,本文仅测试采用2~8个进程时,OD矩阵计算的内存使用情况,如图 6所示。结果表明:采用两个进程时,每个进程的内存开销约为1.2 GB;随着进程数的增加,单进程的内存消耗量逐步降低;采用8个进程时,每个进程的内存开销减少为约0.35 GB。尽管采用8个进程时的总内存消耗量与单进程时基本一致,但是分布式的存储机制充分利用了PC集群中各节点的内存资源,从而有效避免了单节点内存消耗过大的问题。
|
| 图 6 OD矩阵计算的内存开销情况 Fig. 6 Per-process memory consumption of OD matrix computing |
为了测试并行OD矩阵计算过程的效率,应用测试数据进行了相关试验,结果如表 3所示。由表 3可知:随着参与运算的进程数的增加,OD矩阵计算用时在各测试数据中均出现了明显的加速效果。采用两个进程时,算法在各测试数据中的加速比(算法单进程运行时间与多进程运行时间的比值)均在1.81 以上;采用8个进程时,算法加速比均在4.63以上。为了更直观地表示算法时间与进程之间的关系,依据所用进程数和算法运行时间绘制了二者的关系曲线,如图 7所示。由图可见,随着进程数的增加,算法耗时呈下降趋势,加速效果明显。
| 数据集 | 单进程 | 2进程 | 3进程 | 4进程 | 5进程 | 6进程 | 7进程 | 8进程 | ||||||||||||||
| 算法耗时/s | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | ||||||||
| 1 | 28.59 | 14.93 | 1.91 | 10.21 | 2.80 | 7.97 | 3.59 | 6.62 | 4.32 | 5.63 | 5.08 | 5.00 | 5.72 | 4.63 | 6.18 | |||||||
| 2 | 56.35 | 30.32 | 1.86 | 21.36 | 2.64 | 16.84 | 3.35 | 14.26 | 3.95 | 12.63 | 4.46 | 11.20 | 5.03 | 10.68 | 5.27 | |||||||
| 3 | 84.84 | 46.96 | 1.81 | 33.49 | 2.53 | 27.23 | 3.12 | 23.36 | 3.63 | 20.75 | 4.09 | 18.79 | 4.52 | 18.24 | 4.65 | |||||||
| 4 | 61.49 | 31.24 | 1.97 | 21.28 | 2.89 | 16.14 | 3.81 | 13.18 | 4.66 | 11.09 | 5.54 | 10.03 | 6.13 | 9.31 | 6.60 | |||||||
| 5 | 123.37 | 63.24 | 1.95 | 43.33 | 2.85 | 33.52 | 3.68 | 27.56 | 4.48 | 23.46 | 5.26 | 20.65 | 5.98 | 19.83 | 6.22 | |||||||
| 6 | — | 96.12 | — | 67.01 | — | 52.33 | — | 43.28 | — | 37.17 | — | 33.62 | — | 31.76 | — | |||||||

|
| 图 7 并行OD矩阵计算的运行时间 Fig. 7 Running time of parallel OD matrix computing |
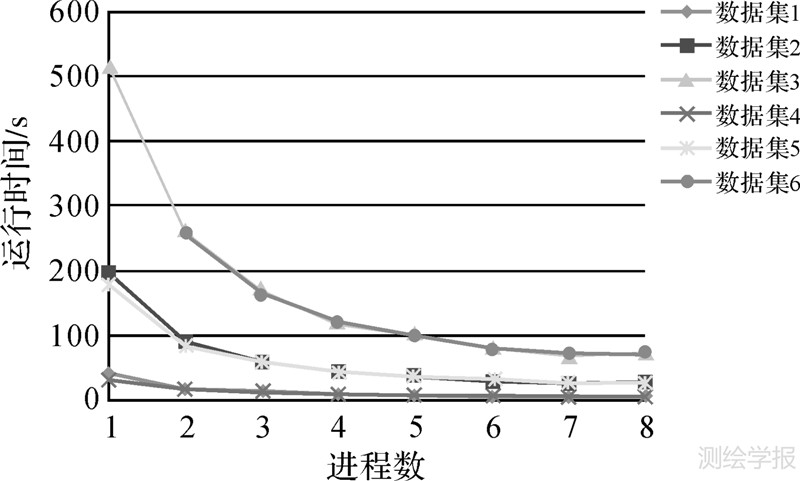
禁忌搜索中的邻域大小直接影响求解的质量和效率。经大量试验得出:邻域大小为(c+w)2/200(c+w为客户点数和车场数之和)时效果最佳;此时,VRP算法能够兼顾计算效率和解质量。并行禁忌搜索过程的运行时间如表 4所示。表 4表明:随着进程数的增加,并行禁忌搜索耗时总体呈下降趋势。在禁忌搜索过程中,新解的生成采用了一些随机方法,以保证解的多样性。这使得生成新解的时间不稳定,导致整个邻域搜索过程的时间出现波动。因此,表 4中测试数据1、2、3、5在多进程计算时,出现了超加速比的情况(表中用黑体表示);在进程数为7和8时产生了耗时波动情况。根据禁忌搜索耗时和进程数的关系绘制它们之间的关系曲线,如图 8所示。由图可见,测试数据1和4、2和5、3和6的曲线基本重合。该结果表明:在不同规模的测试数据中,禁忌搜索的时间主要取决于客户点的数量,与网络规模无关。
| 数据集 | 单进程 | 2进程 | 3进程 | 4进程 | 5进程 | 6进程 | 7进程 | 8进程 | ||||||||||||||
| 算法耗时/s | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | ||||||||
| 1 | 40.39 | 17.35 | 2.33 | 14.96 | 2.70 | 9.36 | 4.31 | 7.98 | 5.06 | 6.84 | 5.90 | 6.10 | 6.62 | 5.89 | 6.85 | |||||||
| 2 | 196.01 | 90.88 | 2.15 | 60.04 | 3.26 | 44.56 | 4.40 | 36.73 | 5.34 | 30.37 | 6.45 | 26.87 | 7.29 | 27.09 | 7.23 | |||||||
| 3 | 515.81 | 259.28 | 1.99 | 170.25 | 3.02 | 117.37 | 4.39 | 98.65 | 5.22 | 81.44 | 6.33 | 68.98 | 7.47 | 72.09 | 7.15 | |||||||
| 4 | 30.92 | 16.18 | 1.91 | 11.05 | 2.79 | 8.75 | 3.53 | 7.61 | 4.06 | 6.72 | 4.60 | 6.89 | 4.48 | 6.13 | 5.05 | |||||||
| 5 | 179.08 | 83.99 | 2.13 | 57.89 | 3.09 | 44.37 | 4.03 | 35.65 | 5.03 | 31.33 | 5.71 | 26.91 | 6.65 | 27.86 | 6.43 | |||||||
| 6 | — | 255.86 | — | 164.56 | — | 122.43 | — | 100.18 | — | 79.57 | — | 72.65 | — | 71.38 | — | |||||||
|
| 图 8 并行禁忌搜索的运行时间 Fig. 8 Running time of parallel VRP algorithm |
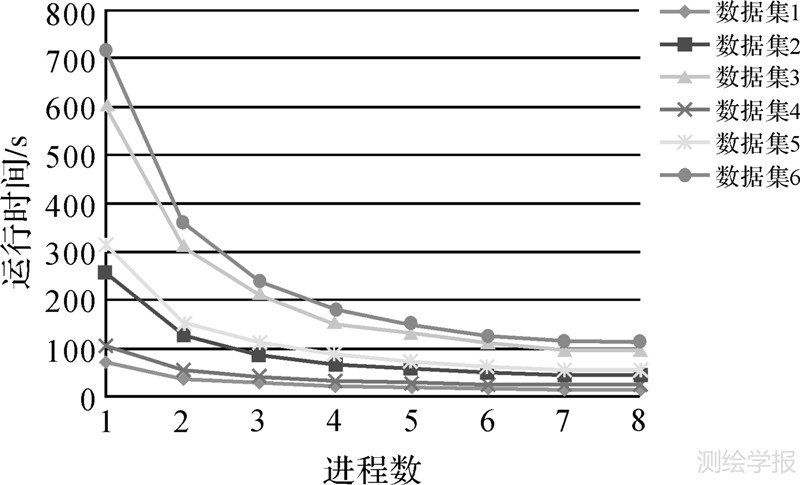
为了对算法的整体效率进行评价,对算法的总用时情况进行统计,结果如表 5和图 9所示。随着进程数的增加,算法的运行时间均呈明显的下降趋势。在测试数据3中的运行时间由单进程时的603.6 s减少为8进程时的95.42 s;采用7~8个进程时,在各测试数据中的算法加速比均在4.46~6.32之间。由此可见,采用并行技术能有效提高算法的运算效率。某些试验结果出现了超加速比的现象(表中用黑体表示),其原因在3.4节中已阐述。
| 数据集 | 单进程 | 2进程 | 3进程 | 4进程 | 5进程 | 6进程 | 7进程 | 8进程 | ||||||||||||||
| 算法耗时/s | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | 算法耗时/s | 加速比 | ||||||||
| 1 | 71.94 | 35.90 | 2.00 | 28.91 | 2.48 | 21.06 | 3.41 | 18.32 | 3.92 | 16.35 | 4.40 | 14.96 | 4.81 | 14.52 | 4.95 | |||||||
| 2 | 255.40 | 128.31 | 1.99 | 86.96 | 2.93 | 66.78 | 3.82 | 57.16 | 4.47 | 48.34 | 5.28 | 42.45 | 6.02 | 42.46 | 6.01 | |||||||
| 3 | 603.61 | 308.37 | 1.95 | 206.57 | 2.92 | 149.10 | 4.04 | 131.64 | 4.58 | 109.52 | 5.51 | 95.59 | 6.31 | 95.42 | 6.32 | |||||||
| 4 | 102.54 | 54.83 | 1.87 | 40.23 | 2.55 | 32.40 | 3.16 | 28.29 | 3.62 | 25.16 | 4.07 | 22.99 | 4.46 | 22.99 | 4.46 | |||||||
| 5 | 313.22 | 153.89 | 2.04 | 110.58 | 2.83 | 85.92 | 3.64 | 72.13 | 4.34 | 62.78 | 4.99 | 56.21 | 5.57 | 55.49 | 5.64 | |||||||
| 6 | — | 359.21 | — | 240.07 | — | 180.84 | — | 148.27 | — | 125.79 | — | 114.39 | — | 112.09 | — | |||||||
|
| 图 9 并行VRP算法的运行时间 Fig. 9 Running time of parallel VRP algorithm |
为了验证计算结果的正确性,本文将算法的运行结果与ArcGIS进行了对比。首先,将测试数据导入ArcGIS中,用ArcGIS的VRP分析工具求出运输路径的目标函数值。结果如表 6所示,测试数据1—6的目标函数值见栏目“ArcGIS结果”。然后,将本文算法的计算结果与上述结果进行比较,用偏差率表示其差异性

| 数据集 | ArcGIS结果/km | 目标函数值的偏差率/(%) | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 平均值 | ||
| 1 | 31 920.3 | 1.23 | 1.96 | 1.63 | 1.38 | 2.98 | 1.39 | 2.66 | 3.61 | 2.11 |
| 2 | 48 884.3 | 1.73 | 2.20 | 1.75 | 1.80 | 2.85 | 2.64 | 2.97 | 2.95 | 2.36 |
| 3 | 63 479.0 | 2.10 | 2.39 | 2.07 | 3.06 | 3.56 | 2.85 | 2.30 | 3.13 | 2.68 |
| 4 | 49 362.1 | 1.78 | 2.61 | 1.92 | 1.89 | 2.16 | 2.73 | 1.77 | 2.05 | 2.11 |
| 5 | 75 412.1 | 2.07 | 2.15 | 3.19 | 2.14 | 2.70 | 2.28 | 2.68 | 3.95 | 2.64 |
| 6 | 99 017.4 | — | 2.43 | 2.61 | 2.91 | 2.51 | 2.97 | 2.70 | 3.96 | 2.87 |
针对图论VRP问题的并行算法已有较多研究成果,但是在地理网络VRP中的实际应用以及针对特定并行环境的算法中,还有很多问题需要解决。本文提出的基于PC集群环境的并行VRP算法,通过分布式存储结构充分利用集群的内存资源,有效避免了求解地理网络VRP时单节点内存不足的问题;同时,采用精简的通信策略以及基于邻域分解的并行禁忌搜索算法,大幅提升了计算效率。基于模拟路网数据的相关试验表明:本文算法能够在保证计算精度的前提下(平均偏差率在2.11%~2.87%之间)高效地求解大规模地理网络VRP问题,且具有良好的扩展性;同时能够在PC集群环境中获得良好的加速性能,采用8个进程时的算法加速比在4.46~6.32之间。此外,本文研究着重于PC集群环境下的并行化方法,核心的求解算法仅采用了基本的禁忌搜索。因此,在求解质量方面本文算法还有很大的提升空间。下一步研究工作将引入更高级的策略对禁忌搜索过程进行优化,进一步提升求解质量。
| [1] | LIU Xia. Research on Vehicle Routing Problem [D]. Wuhan:Huazhong University of Science and Technology,2007.(刘霞.车辆路径问题的研究[D]. 武汉:华中科技大学,2007.) |
| [2] | LI Jun,GUO Yaohuang. Theories and Methods of Vehicle Scheduling Optimization [M]. Beijing:Chinese Materials Press,2001.(李军,郭耀煌. 车辆优化调度理论与方法[M]. 北京:中国物资出版社,2001.) |
| [3] | XIAO Han,ZHANG Zuxun. Parallel Image Matching Algorithm Based on GPGPU [J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):46-51.(肖汉,张祖勋. 基于GPGPU的并行影像匹配算法[J]. 测绘学报,2010,39(1):46-51.) |
| [4] | ZHAO Yuan,ZHANG Xinchang,KANG Tingjun. A Parallel Ant Colony Optimization Algorithm for Site Location [J]. Acta Geodaetica et Cartographica Sinica,2010,39(3):322-327.(赵元,张新长,康停军. 并行蚁群算法及其在区位选址中的应用[J]. 测绘学报,2010,39(3):322-327.) |
| [5] | ZOU Xiancai,LI Jiancheng,WANG Haihong,et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity [J]. Acta Geodaetica et Cartographica Sinica,2010,39(6):636-641.(邹贤才,李建成,汪海洪,等. OpenMP并行计算在卫星重力数据处理中的应用[J]. 测绘学报,2010,39(6):636-641.) |
| [6] | SHEN Jie, GUO Lishuai, ZHU Wei, et al. Parallel Computing Suitability of Contour Simplification Based on MPI [J]. Acta Geodaetica et Cartographica Sinica,2013,42(4):621-628.(沈婕,郭立帅,朱伟,等. 消息传递接口环境下等高线简化并行计算适宜性研究[J]. 测绘学报,2013,42(4):621-628.) |
| [7] | MAISCHBERGER M,CORDEAU J. Solving Variants of the Vehicle Routing Problem with a Simple Parallel Iterated Tabu Search,in Network Optimization [M]. Berlin:Springer,2011:395-400. |
| [8] | CORDEAU J,MAISCHBERGER M. A Parallel Iterated Tabu Search Heuristic for Vehicle Routing Problems [J]. Computers and Operations Research,2012,39(9):2033-2050. |
| [9] | GROЁR C,GOLDEN B,WASIL E. A Parallel Algorithm for the Vehicle Routing Problem [J]. INFORMS Journal on Computing,2011,23(2):315-330. |
| [10] | JIN J Y,CRAINIC T G,LOKKETANGEN A. A Parallel Multi-neighborhood Cooperative Tabu Search for Capacitated Vehicle Routing Problems [J]. European Journal of Operational Research,2012,222(3):441-451. |
| [11] | RIBEIRO G M,LAPORTE G. An Adaptive Large Neighborhood Search Heuristic for the Cumulative Capacitated Vehicle Routing Problem [J]. Computers and Operations Research,2012,39(3):728-735. |
| [12] | ZHU Haodong,LI Hongchan. Parallel Tabu Search Algorithm Based on Double Tabu Objects [J].Computer Engineering and Applications,2011,47(29):31-33.(朱颢东,李红婵. 基于双禁忌对象的并行禁忌搜索算法[J]. 计算机工程与应用,2011,47(29):31-33.) |
| [13] | SHI Yarong,WAN Difang,LI Shuangyan,et al. Research of Vehicle Routing Problem Based on GIS [J]. System Engineering Theory and Practice,2009,29(10):76-84.(史亚蓉,万迪昉,李双燕,等. 基于GIS的物流配送路线规划研究[J]. 系统工程理论与实践. 2009,29(10):76-84.) |
| [14] | KEENAN P. Modeling Vehicle Routing in GIS [J]. Operational Research,2008,8(3):201-218. |
| [15] | BOYER V,ELKIHEL M,BAZ D E. Heuristics for the 0-1 Multidimensional Knapsack Problem[J].European Journal of Operational Research,2009,199(3):658-664. |
| [16] | GENDREAU M,POTVIN J Y. Handbook of Metaheuristics [M]. Norwell:Kluwer Academic Publishers,2010:41-60. |
| [17] | ZACHARIADIS E E,TARANTILIS C D,KIRANOUDIS C T. A Guided Tabu Search for the Vehicle Routing Problem with Two-dimensional Loading Constraints [J]. European Journal of Operational Research,2009,195(3):729-743. |
| [18] | LI Zhiping,GAO Xingguo. Comparison Analysis of Simulated Annealing and Tabu Search for VRP [J]. Science Information,2010,22:79-80.(李志萍,高兴国. 模拟退火法与禁忌搜索法求解VRP的对比分析[J]. 科技信息,2010,22:79-80.) |
| [19] | BOLDUC M C,LAPORTE G,RENAUD J,et al. A Tabu Search Heuristic for the Split Delivery Vehicle Routing Problem with Production and Demand Calendars [J]. European Journal of Operational Research,2010,202(1):122-130. |
| [20] | NGUEVEU S U,PRINS C,CALVO R W. A Hybrid Tabu Search for the m-peripatetic Vehicle Routing Problem,in Matheuristics [M]. New York:Springer,2010:253-266. |
| [21] | BRANDO J. A Tabu Search Algorithm for the Heterogeneous Fixed Fleet Vehicle Routing Problem [J]. Computers and Operations Research,2011,38(1):140-151. |
| [22] | CESCHIA S,GASPERO L D,SCHAERF A. Tabu Search Techniques for the Heterogeneous Vehicle Routing Problem with Time Windows and Carrier-dependent Costs [J]. Journal of Scheduling,2011,14(6):601-615. |
| [23] | MOCCIA L,CORDEAU J F,LAPORTE G. An Incremental Tabu Search Heuristic for the Generalized Vehicle Routing Problem with Time Windows [J]. Journal of the Operational Research Society,2011,63(2):232-244. |


