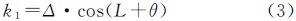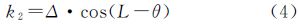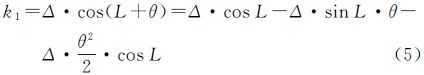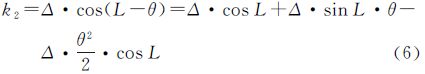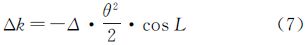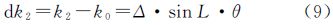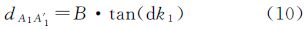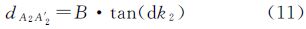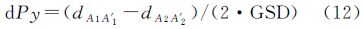2. 地理信息工程国家重点实验室,陕西 西安 710054;
3. 西安测绘研究所,陕西 西安 710054
2. National Key Laboratory of Geo-Information Engineering,Xi’an 710054,China;
3. Xi’an Institute of Surveying and Mapping,Xi’an 710054,China
1 引 言
卫星摄影测量是航天对地观测的重要手段,根据摄影任务及需求不同,摄影测量卫星包括全球连续覆盖和局部区域覆盖两种:局部区域覆盖主要针对热点地区地理信息数据的获取,目前美国在轨飞行的各类高分辨率商业卫星大都用于局部覆盖;全球连续覆盖用于获取和建立全球基础地理信息数据,通常利用线阵CCD立体相机或干涉雷达测量方式予以实现。
光学卫星摄影测量常用的相机载荷包括单线阵相机、两线阵相机和三线阵相机[1],单线阵相机主要通过摇摆成像获取立体影像[2, 3],两线阵相机和三线阵相机在卫星飞行中,可以利用相机的结构设计,实现立体影像获取[1]。在以两线阵或三线阵相机为主要载荷的卫星系统中,为了解决地球自转引起的线阵影像立体重叠范围变窄的影响,卫星实施偏流角修正技术,保持立体影像有效覆盖区域[4]。美国StereoSat卫星方案中提到了偏流角修正问题[5],但由于卫星工程未能立项而没有深入研究。偏流角修正技术措施不严格会产生偏流角改正余差,并随着纬度的变化而变化,使得线阵立体相机在不同摄影时刻对同一地面点摄取的影像,恢复立体模型时不相交于一点,产生明显的上下视差。
本文通过对偏流角改正余差对上下视差机理分析,建立了偏流角改正余差影响上下视差的模型,提出通过相机参数在轨标定和光束法中外方位角元素低频补偿技术加以改正的思路,实现无地面控制点条件下定位精度及其全球一致性,并将该方法运用于天绘一号卫星影像地面处理中,取得了较好效果。
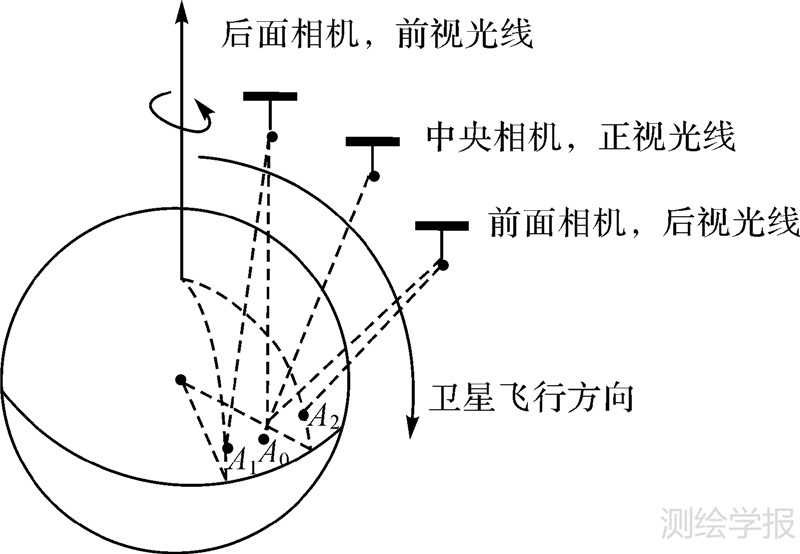
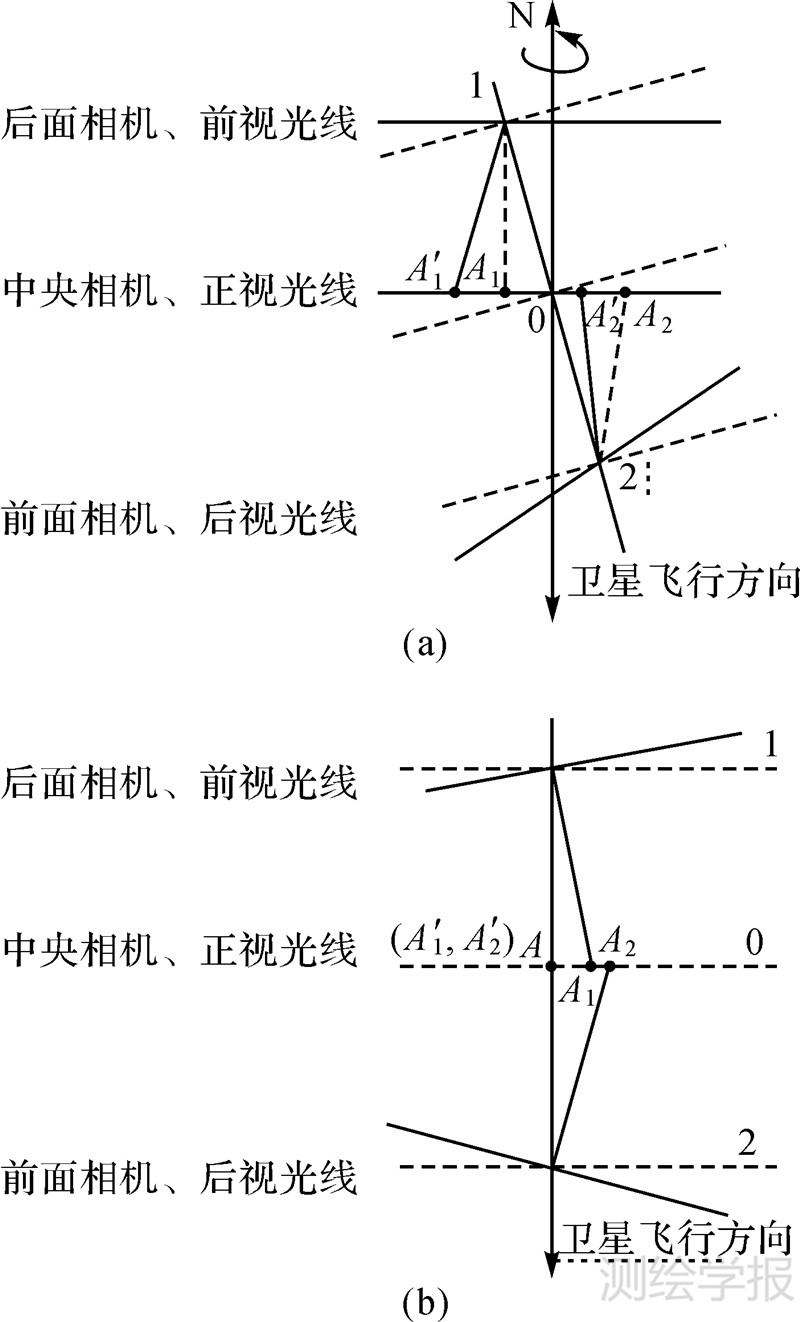
2 偏流角改正对视差的影响及改正 2.1 偏流角改正余差引起上下视差的机理分析由于地球自转,三线阵相机在不同摄影时刻对同一地面点摄取的影像,分别为A1、A0、A2,如图 1所示[6]。中央相机按其摄影时刻T0对应的纬度计算出对应偏流角k0,进行偏流角改正;前面相机按其摄影时刻T1对应的纬度计算出对应偏流角k1,进行偏流角改正;后面相机按其摄影时刻T2对应的纬度计算出对应偏流角k2,进行偏流角改正。从原理上讲,为了3个点交于一点,以中央相机为基准,将前面相机的后视光线旋转一个角度k0,使A2与A0重合,后面相机的前视光线也旋转一个角度k0,使A1也重合于A0,如图 2中使A′1到A1,A′2到A2。但由于相机是一个整体,实际卫星摄影测量中无法实现严格旋转改正使3个点交于一点。因此,在不同摄影时刻,其旋转角度不同,使得k1与k0不等,k2也与k0不等,在恢复立体模型时,3个相机所摄影同一地面点的影像并不相交于一点,会产生明显的上下视差,并且随纬度变化而变化。
|
| 图 1 偏流角改正余差示意图 Fig. 1 Residual of drift angle correction |
|
| 图 2 偏流角改正余差引起上下视差示意图 Fig. 2 Vertical parallax caused by residual of drift angle correction |
偏流角问题已有许多学者作过讨论[4, 7],并有严格的计算公式,为了定性分析偏流角修正措施理论上不严格对摄影测量平差的影响,本文采用偏流角近似计算公式[5]
式中,k为偏流角;Δ为偏流角最大值,根据文献[4]取值为3.82°;L为摄影时刻的纬度值。中央相机、前面相机及后面相机偏流角分别为
式中,θ为基线B(前面相机与中央相机或后面相机与中央相机的距离)对应的纬度值差,约为1.895°=0.033 073 9弧度[4],将式(3)、(4)分别按麦克劳林公式展开至二次得 公式(5)、(6)由Δ·cosL-Δ·sinL·θ(或Δ·cosL+Δ·sinL·θ)和-Δ·θ2/2·cosL两部分组成,其中前两项是相对于中央相机而言,是造成上下视差的主要因素,理论分析将达到100多像素。由于星敏感器等测姿设备所测定的偏航方向中已包含该角度,利用外方位元素进行直接交会投影时[8],大部分视差可被消除,剩余视差大约在几个像素量级,在光束法平差中作为初值代入进行循环迭代计算后,将改善至1/3像素级;后半部分系偏流角增量,令 其性质与星地相机夹角转换参数δκ性质相同,并且随纬度变化,必须在相机参数标定和具体航线平差中对Δk分别进行改正。由公式(2)、(5)及(6),可得出前面、后面相机与中央相机偏流角间较差为
根据图 2所示,A1到A′1,A2到A′2距离分别为
因此,由偏流角造成的上下视差为
式中,GSD为像元地面分辨率。 2.3 偏离角修正后的余差影响分析根据天绘一号卫星的技术状态,利用卫星状态参数,对不同纬度偏流角改正余差引起的上下视差和改正系统量Δκ进行理论分析。提出在无地面控制点条件下通过等效框幅像片(equivalent frame photo,EFP)平差进行相机参数在轨标定,并采用具有低频误差补偿的EFP全三线交会区光束法平差[6, 9],对2.2节中提到的两类偏流角造成的上下视差进行合理的改正。
分析采用的卫星参数:像元地面分辨率5m,轨道高500km,前、后视相机与正视相机夹角为25°。根据公式(1)、(12)及(7),分别计算偏流角k、dPy及Δκ,其结果如表 1所示。在轨标定后Δκ相对于标定场的变化量,如表 2所示。
| L/(°) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| k/(°) | 3.82 | 3.76 | 3.58 | 3.30 | 2.92 | 2.45 | 1.91 | 1.30 | 0.66 |
| dPy/像素 | 0 | 18 | 35 | 51 | 66 | 79 | 89 | 97 | 101 |
| Δκ/(″) | -7 | -7 | -7 | -6 | -5 | -4 | -3 | -2 | -1 |
| L/(°) | -80 | -60 | -50 | -40 | -20 | 0 | 20 | 40 | 50 | 60 | 80 |
| Δκ相对标定场变化量/(″) | 4 | 2 | 0 | 0 | -2 | -2 | -2 | 0 | 0 | 2 | 4 |
从表 1、2中看出:
(1) 偏流角随纬度的变化而变化,其改正余差影响上下视差可达100多像素。
(2) 进行相机参数标定后,偏流角改正系统量Δκ量级略有缩小,但仍随纬度发生变化,与标定场(纬度在40°~50°)Δκ改正量相比,最大量级达到4″,相机参数标定无法对其他纬度航线中的Δκ差异进行改正,需在具体航线平差中进行低频误差补偿。
3 在轨标定及光束法平差中偏流角改正余差处理为了实现卫星影像无地面控制点条件下的高精度定位,测绘卫星必须采用相机参数在轨标定技术[10, 11, 12]。与其他卫星相机参数在轨标定不同,天绘一号卫星相机参数在轨数学模型是以反解空中三角测量为基础,采用等效框幅式影像构网的思想,并采用了LMCCD相机(line-matrix CCD camera)影像EFP光束法平差技术[13, 14]。相机参数在轨标定航线偏流角引起上下视差至100多像素,即使根据实验室标定参数进行前方交会,上下视差依然有10~20像素。在光束法平差中按EFP原理构建一系列的双模型航线,偏流角改正余差可看作常规航空摄影测量中的旋偏角进行改正处理,使上下视差减小至0.5像素左右。
相机参数在轨标定结果中星地相机夹角的改正数δk只是包含本次标定数据中的Δκ改正。不同纬度航线的Δκ会有差异,需在具体航线光束法平差过程中进一步改正。带有低频误差补偿的EFP全三线交会光束法平差[6, 9],其本质是在传统平差解算6个外方位元素的基础上,增加公共φ和公共κ量的改正功能,经过在轨标定参数转换后的外方位角元素κ当作近似值参与迭代计算,可消除2.2节部分提到的偏流角改正余差造成的上下视差,光束法平差后外方位角元素中已包含了偏流角余差的改正值,所建立的立体模型无明显的上下视差,可实现无地面控制点条件下的高精度定位。
4 实际影像数据处理试验与分析 4.1 偏流角改正余差光束法平差示例利用天绘一号01星卫星影像进行偏流角改正余差影响上下视差试验。首先选择2011-04-12摄影数据,影像长度约300km,采用相应的相机标定参数和实验室标定[15]参数进行视差改正统计,其结果如表 3所示。
| 上下视差/像素 | 定位精度/m | 检查点数量 | |||
| μXY | μZ | μXYZ | |||
| 同名像点量测后 | 140 | 84 | |||
| 前方交会(相机实验室标定参数) | 6.4 | 163.3 | 39.4 | 168.1 | 6 |
| 前方交会(相机在轨标定参数) | 1.7 | 9.1 | 9.1 | 12.9 | 6 |
| 光束法平差(相机在轨标定参数) | 0.3 | 10.1 | 5.9 | 11.8 | 6 |
表中,μXY为高斯6°分带平面坐标均方根误差(RMS)[16];μZ为大地高误差;μXYZ为3轴坐标综合均方根误差。从表 3看出:
(1) 受偏流角改正余差影响,立体影像同名像点量测后,其上下视差较大,达140多像素。
(2) 利用实验室标定参数将同名像点投影到地面时,外方位角元素κ中已包含摄影时刻的偏流角改正值,前方交会后,其上下视差约为6.4像素。
(3) 利用相机在轨标定参数将同名像点投影到地面时,外方位角元素κ中已包含摄影时刻的偏流角改正值,前方交会后,其上下视差约为1.7像素。
(4) 相机参数标定过程中对Δκ进行改正,具体体现在标定结果δk中,采用相机在轨标定参数进行光束法平差后,上下视差可提高至0.3像素,同时定位精度也有明显改善。
4.2 光束法平差公共的俯仰和偏航方向补偿示例从表 2中看出,标定结果在不同纬度地区Δκ约有4″的差异,此外星地相机夹角的改正数还随时间存在Δφ、Δκ的慢变化[17]。因此,必须在具体航线光束法平差中进行低频误差补偿予以处理。为此选定2011-12-22的摄影数据,影像长度约150km。并利用2010年10月获取东北试验场数据对相机参数进行系统标定,利用该标定参数对2011-12-22数据进行低频误差补偿试验。试验数据与标定结果在时间上相差一年多,星地相机夹角随时的变化比较明显,适宜于作为本次低频误差补偿试验。试验结果如表 4所示。
| 定位精度/m | 星地相机夹角改正数/(″) | 检查点数量 | ||||||
| μXY | μZ | μXYZ | δφ | δw | δk | |||
| 相机在轨标定参数前方交会(2010年10月标定结果) | 36.9 | 8.2 | 37.9 | -19.7 | -66.1 | -17.2 | 18 | |
| 相机在轨标定参数光束法平差(低频误差补偿后) | 15.2 | 5.9 | 16.4 | -10.2 | -66.1 | -37.1 | 18 | |
从表 4看出:
(1) 随着纬度变化、特别是摄影时间与在轨标定时间相差一年多,定位精度误差较大,主要是由姿态测定系统变化而引起的。为了实现全球定位精度的一致性,需对姿态测定系统的低频误差进行补偿。
(2) 低频误差补偿主要对俯仰方向δφ和偏航方向δk进行补偿,本例中δφ补偿大约-9.5″,δk补偿大约20″,因而使定位精度由37m提高至16.4m。与标定场相比,在不同纬度地区Δκ约4″的差异也被进行补偿处理,使低频误差补偿中δk项包含对Δκ差异的补偿。
5 结 论本文从理论上分析了偏流角对上下视差的影响,结合相机参数在轨标定技术,指出由于受纬度影响,在具体航线光束法平差中采用低频误差补偿技术,可保证无地面控制点条件下定位精度,并保持精度在全球范围的一致性。天绘一号卫星地面处理系统利用本文提出的偏流角改正余差的方法,使天绘一号01星无地面控制点目标定位精度达到美国SRTM相对精度水平[18],实现了无地面控制点条件下测制1∶5万比例尺(等高线间距20m)地形图的目标[19, 20]。
| [1] | WANG Renxiang. Satellite Photogrammetric Principle for Three-line Array CCD Imagery[M]. Beijing: Publishing House of Surveying and Mapping, 2006. (王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2006.) |
| [2] | SCHAP N. IKONOS: Future and Present[C]//Proceedings of SPIE, Symposium on Sensors, Systems, and Next-generation Satellites VI.[S.l.]:SPIE,2003:660-668. |
| [3] | NASINI R, ROSSI L, VOLPE F. Expanding Operational Applications of Very High Resolution Remote Sensing: QuickBird[C]//Proceedings of SPIE, Symposium on Sensors, Systems, and Next-generation Satellites VI.[S.l.]:SPIE,2003: 493-502. |
| [4] | HU Xin, CAO Xibin. The Correction of Drift Angle of the Three-line Array Mapping Satellite[J]. Journal of Geomatics Science and Technology, 2006, 23(5): 321-324.(胡莘, 曹喜滨. 三线阵测绘卫星的偏流角改正问题[J]. 测绘科学技术学报, 2006, 23(5): 321-324.) |
| [5] | ITEK Corporation. Conceptual Design of an Automated Mapping Satellite System(Mapsat)[R]. Alexandria: National Technical Information Service, 1981. |
| [6] | WANG Jianrong, WANG Renxiang. EFP Multi-functional Bundle Adjustment of Mapping Satellite-1 without Ground Control Points[J]. Journal of Remote Sensing, 2013, 16(S1): 112-115. (王建荣, 王任享. 天绘一号卫星无地面控制点EFP多功能光束法平差[J]. 遥感学报, 2013, 16(S1): 112-115.) |
| [7] | WANG Xinyi, ZHANG Jianqing, HU Yan, et al. Analysis of Geopositioning of Satellite Three-line-array CCD Caused by Drift Angle[J]. Geomatics and Information Science of Wuhan University, 2013,38(3): 283-286.(王新义, 张剑清, 胡燕,等. 偏流角对卫星三线阵CCD影像定位的影响分析[J]. 武汉大学学报:信息科学版, 2013, 38(3): 283-286.) |
| [8] | WANG Zhizhuo. Principle of Photogrammetry[M]. Beijing: Publishing House of Surveying and Mapping, 1990. (王之卓. 摄影测量原理[M]. 北京:测绘出版社, 1990.) |
| [9] | WANG Renxiang. Bundle Adjustment of Satellite Borne Three-line Array CCD Image[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 379-385.(王任享. 卫星三线阵CCD影像光束法平差研究[J]. 武汉大学学报: 信息科学版,2003, 28(4): 379-385.) |
| [10] | SRINIVASAN T P, ISLAM B, SANJAY K,et al. In-flight Geometric Calibration: An Experience with Cartosat-1 and Cartosat-2[C]//Proceedings of ISPRS XXI Congress.[S.l.]:ISPRS, 2008:83-88. |
| [11] | WANG Renxiang, WANG Jianrong, ZHAO Fei, et al. Dynamic Calibrating of Three-line-array CCD Camera in Satellite Photogrammetry Using Ground Control Point[J]. Journal of Earth Sciences and Environment, 2006, 28(2): 1-5.(王任享, 王建荣, 赵斐,等. 利用地面控制点进行卫星摄影三线阵CCD相机的动态检测[J]. 地球科学与环境学报, 2006, 28(2): 1-5.) |
| [12] | LI Deren. China’s First Civilian Three-line-array Stereo Mapping Satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322. (李德仁. 我国第一颗民用三线阵立体测图卫星:资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317-322.) |
| [13] | WANG Renxiang, HU Xin, YANG Junfeng, et al. Proposal LMCCD Camera for Satellite Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 116-120. (王任享, 胡莘, 杨俊峰,等. 卫星摄影测量LMCCD摄影机的建议[J]. 测绘学报, 2004, 33(2): 116-120.) |
| [14] | WANG Renxiang, WANG Jianrong, WANG Xinyi, et al. The Satellite Photogrammetric Performance of LMCCD Camera[J]. Science of Surveying and Mapping, 2004, 29(4): 10-12.(王任享, 王建荣, 王新义,等. LMCCD相机卫星摄影测量的特性[J]. 测绘科学, 2004, 29(4): 10-12.) |
| [15] | LIU Jinguo, LI Jie, HAO Zhihang. Study on a Geometric Calibration Method for Three-linear-array CCD Camera with Sub-pixel Accuracy[J]. Opto-Electronic Engineering, 2004, 31(1): 36-39. (刘金国, 李杰, 郝志航. 三线阵CCD相机亚像元精度几何标定方法研究[J]. 光电工程, 2004, 31(1): 36-39.) |
| [16] | YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(5):646-650. (杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报,2012,41(5):646-650.) |
| [17] | WANG Renxiang, WANG Jianrong, HU Xin. Study on the Photogrammetry of In-flight Satellite without Ground Control Point[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1261-1264. (王任享, 王建荣, 胡莘. 在轨卫星无地面控制点摄影测量探讨[J]. 武汉大学学报:信息科学版, 2011, 36(11): 1261-1264.) |
| [18] | USGU.SRTM Shuttle Radar Topography Misson[EB/OL]. [2010-10-16]. http://www.jpl.nasa.gov/srtm. |
| [19] | WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 1-5. (王任享, 胡莘, 王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1): 1-5.) |
| [20] | WANG Renxiang, HU Xin, WANG Xinyi, et al. The Construction and Application of Mapping Satellite-1 Engineering[J]. Journal of Remote Sensing, 2013, 16(S1): 2-5. (王任享, 胡莘, 王新义,等. 天绘一号卫星工程建设与应用[J]. 遥感学报,2013, 16(S1): 2-5.) |