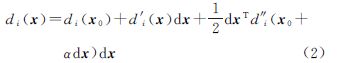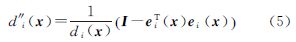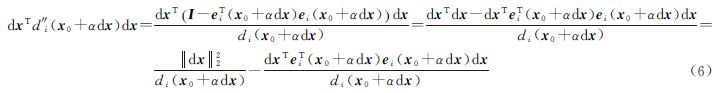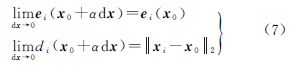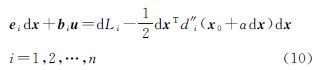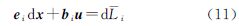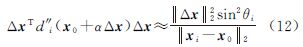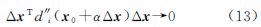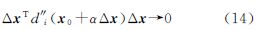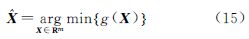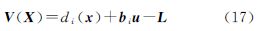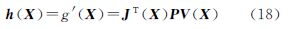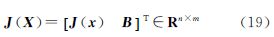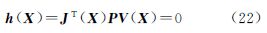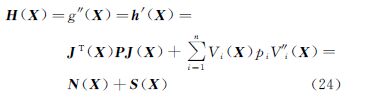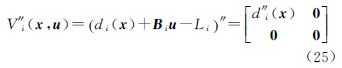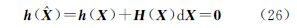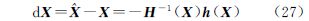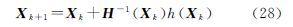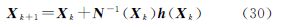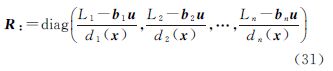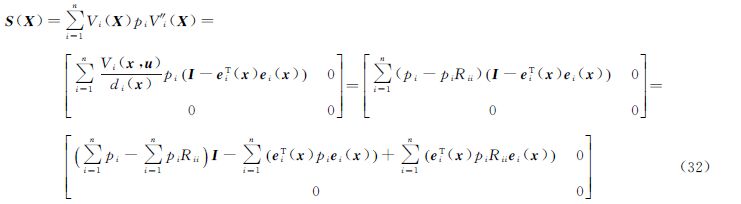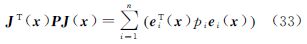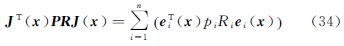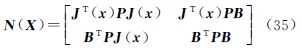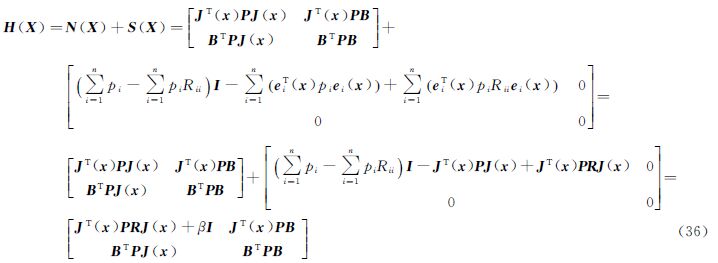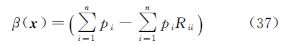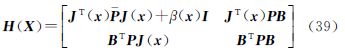2. 中国测绘科学研究院，北京 100830；
3. 西安测绘研究所 地理信息工程国家重点实验室，陕西 西安 710054
2. Chinese Academy of Surveying and Mapping,Beijing 100830,China；
3. National Key Laboratory of Geo-Information Engineering，Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China
大地测量数据处理所涉及的观测模型一般为非线性模型[1, 2]。线性最小二乘法处理非线性平差模型的数学基础为平差函数模型的一阶泰勒级数逼近，这要求线性化初值充分接近问题的解且平差函数模型的非线性强度较低[3]。非线性平差是国内外研究的难点和热点问题，从微分几何的观点出发，模型的固有曲率和参数效应曲率是刻画非线性模型非线性强度的重要指标[4]。文献[5, 6]论述了经典测量平差理论处理非线性的适用条件。文献[7]从扰动分析角度讨论了非线性平差的收敛稳定性问题，并指出非线性扰动主要来自线性近似时系数矩阵的扰动、附加的截断误差及近似正交过程。在参数估值非线性误差传播精度评定方面，也取得了大量研究成果[8]。
距离观测在测量中具有极其重要的地位，在诸如大地测量在内的各种高精度测距定位应用，除了确定待定点的点位坐标参数，还需要附加一些多余参数以精化平差函数模型，其有关平差模型都是非线性的。当平差模型的非线性强度较高时，选取不同初始值及近似正交过程可导致线性近似引起的系数矩阵扰动和截断误差偏大，此时又常采用正则化迭代解法。常用的测距观测方程非线性平差方法有高斯-牛顿法、扩展牛顿迭代法[9, 10, 11]。文献[2]指出不稳定性是病态问题的重要特征之一。文献[12]指出，高斯-牛顿迭代法处理病态测距方程时成功率较低。文献[13]提出了一种似解析非线性平差解法，该解法的基本思想起源于高斯-雅克比组合平差方法[14]。
本文在测距定位观测方程非线性分析的基础上，导出了距离函数二阶残余项的估计公式，以及附加多余参数的测距定位方程非线性平差的牛顿迭代公式，讨论了封闭牛顿迭代公式退化为高斯-牛顿迭代法的条件。最后以GPS长距离伪距定位方程和短距离病态测距定位方程非线性平差为例，验证了本文的主要结论。
附加多余参数的测距定位观测方程可表示为
式中，x为待定点位置坐标参数；di(x)=
为第i个已知点xi至待定点的欧氏距离；u为多余参数；bi为多余参数映射为距离观测改正的系数矩阵；Li为观测值。本文讨论均以空间定位为例，即假定x=[x y z]T∈R3。
下面讨论观测方程(1)的线性化近似条件。对于第i个距离函数di(x)在x0处的泰勒级数展开为[6]
式中，α∈(0,1)；dx=x－x0为自变量微分
距离函数的二阶偏导数式(4)还可见于文献[4, 6, 12]。在导航定位领域，常记ei(x):=d′i(x)，其几何意义为观测方向余弦。事实上，式(4)可简记为
式(5)建立了距离函数一阶导数与二阶导数的关系，这在下面推导中有重要应用。
2.3 距离函数线性化误差分析下面讨论式(2)中二阶残余项的性质。结合函数(5)可得
图 1给出了式(6)中各项的几何意义。设初值精度足够高，即dx→0。由于α∈(0,1)，则αx总落在向量x上，且由极限
|
| 图 1 二阶残余项的几何意义 Fig. 1 Geometrical meaning of the second-order remainder |
可得
将式(2)代入式(1)可得
将残余项12dxTd″i(x0+αdx)dx≥0归入随机模型，可得
若记d Li=dLi－dxTd″i(x0+αdx)dx/2，则平差函数模型式(10)可表示为
可见，线性化残余项会损失观测精度，这对线性化平差模型将产生系统性影响。若使用误差向量Δx替代微分dx，则
(1) 当||xi－x0||2→∞或Δx→0时，即已知点距离待定点无穷远或误差向量足够小时
(2) 当θi→0或θi→π时，即当误差向量方向Δx与观测方向重合时，总存在
当n个控制点均匀分布于三维空间时，条件(2)无法对每个观测方程均成立。因此，xi－x02→∞或Δx→0是距离函数线性化近似的重要前提条件。当距离较短时，线性化误差不容忽视，应考虑非线性方法确定问题的解，而当距离观测值较大且初值较为接近问题的解时，可忽略线性化误差影响。
3 封闭牛顿迭代公式 3.1 非线性测量平差的正交条件记X:=∈Rm为由位置参数和多余参数构成的待估参数向量，方程(1)的非线性最小二乘解为
式中
为残差向量加权二次型，P=diag(p1,p2，…,pn)为观测权阵
为残差向量。
函数g:Rn→R的方向导数为
式中
为非线性方程(1)的雅克比矩阵(设计矩阵)
由自由极值可得，非线性最小二乘解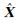
满足正交条件
方程(22)为相容非线性方程组，其解即为方程(1)的非线性最小二乘解。
3.2 牛顿迭代法和高斯-牛顿迭代法下面构造求解方程(22)的迭代计算公式。方向导数h(X)的微分表达式为[16]
式中
令dX=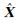－X，则联立式(22)和式(23)可得
若det(H(X))≠0，则
由微分式(27)可构造牛顿迭代公式
结合式(24)和(25)可知，当V(X)→0或min{di(x)}→∞时
此时，牛顿迭代公式退化高斯-牛顿迭代公式，即
矩阵S(X)在文献[4]中采用了立体矩阵记法。当观测数量很大时，计算矩阵S(X)需要花费大量存储和计算成本。
3.3 封闭牛顿迭代公式为避免矩阵S(X)的存储和计算成本，下面推导海森矩阵H(X)的压缩记法。记
结合式(25)可得
由关系式
以及
可导出
式中
为阻尼因子或正则化因子。由压缩后的海森矩阵式(36)可得封闭牛顿迭代公式为
式中
式中，P=diag(R1p1,R2p2,…,Rnpn)，Ri=Li－biu/di(x)。
当距离观测相对精度足够高时，由R→I，可导出β(x)→0，封闭牛顿迭代法退化为高斯-牛顿迭代法。当使用式(39)计算海森矩阵H(X)时，仅需在高斯-牛顿迭代公式的基础上，计算矩阵和阻尼因子β(x)。对于病态定位方程，封闭牛顿迭代公式中的阻尼因子β(x)有望改善迭代序列的收敛性和稳定性。
4 算 例算例1：GPS伪距单点定位。表 1给出了8颗GPS卫星的改正伪距观测值(多余参数为钟差参数)。分别利用高斯-牛顿迭代法和封闭牛顿迭代法对GPS伪距定位方程进行平差，迭代初值
X0=[220 145.906 -2 182 735.237 4 385 742.088 4 70 625.992]
由表 1给出的前4颗卫星解析确定[17, 18]，迭代终止条件为||Xk+1-Xk|| ＜10－5。
| m | |||||
| 卫星号 | 卫星坐标 | 原始伪距 | 改正伪距 | ||
| x | y | z | |||
| 1 | -15 788 120.404 7 | 19 485 331.990 1 | -8 416 047.882 6 | 24 030 849.575 0 | 24 074 310.009 2 |
| 3 | -10 061 442.077 5 | 24 169 576.419 5 | 2 979 970.352 6 | 21 513 378.942 1 | 21 542 989.344 8 |
| 7 | -13 035 048.105 7 | -10 006 267.586 0 | 21 206 291.335 4 | 25 042 901.294 0 | 25 090 482.936 3 |
| 13 | 9 567 303.251 4 | 12 255 908.793 5 | 21 430 380.259 7 | 22 552 299.974 1 | 22 611 304.799 6 |
| 16 | -10 183 783.104 2 | 11 595 820.186 7 | 21 679 853.717 8 | 20 811 527.544 1 | 20 861 953.252 8 |
| 19 | -5 801 297.568 2 | 24 385 049.751 6 | -8 485 085.611 1 | 24 092 693.599 1 | 24 109 770.208 4 |
| 23 | 3 332 408.106 3 | 20 465 476.473 3 | 16 386 911.805 3 | 21 155 398.700 1 | 21 212 186.451 3 |
| 31 | -23 697 175.553 8 | 8 778 061.535 2 | 8 494 537.156 7 | 22 615 484.911 1 | 22 619 499.511 9 |
如图 2所示，高斯牛顿迭代法和封闭牛顿迭代法的收敛序列基本相同，两者相差毫米级。算例表明，因GPS卫星距离待定点两万余千米之远，迭代公式(34)和(27)相差甚微。高斯-牛顿迭代法计算成本较低，而封闭牛顿迭代公式计算成本相对较高。当距离观测方程态性良好且距离观测量非常大时，建议使用高斯-牛顿迭代法。
|
| 图 2 点位坐标序列 Fig. 2 Sequence of coordinates |
算例2：短距离病态定位方程。在三维测距定位中，当未知点与已知点近似共面时，测距定位方程的设计矩阵为病态矩阵[19]。在移动蜂窝网三维定位中，基准站和移动终端一般近似分布于地表。短距离病态定位问题还常存在于室内导航定位、三维激光扫描、水下GPS定位等应用场合。
如图 3所示，给出一正六边形蜂窝网(控制点位于正六边形的顶点)一组仿真伪距观测数据。表 2给出的控制点与未知点P(点位真值为[4400 4440 0]近似共面)，法方程系数矩阵的条件数约为9800。分别使用高斯-牛顿迭代法、封闭牛顿迭代法和正则化高斯-牛顿迭代法对该伪距定位问题进行非线性最小二乘平差。3种方法使用相同的初值X0=[4400 44000 0]进行迭代，迭代收敛终止条件为||Xk+1-Xk|| ＜10－5。
|
| 图 3 蜂窝定位网 Fig. 3 Cell network |
| m | ||||
| 点号 | 控制点坐标 | 伪距观测值 | ||
| P1 | 4 000.00 | 0.00 | 5.00 | 4 923.99 |
| P2 | 2 000.00 | 3 464.10 | 10.00 | 3 067.71 |
| P3 | -2 000.00 | 3 464.10 | 15.00 | 6 962.62 |
| P4 | -4 000.00 | 0.00 | 20.00 | 9 975.28 |
| P5 | -2 000.00 | -3 464.10 | 25.00 | 10 627.00 |
| P6 | 2 000.00 | -3 464.10 | 30.00 | 8 711.36 |
正则化高斯-牛顿迭代公式为[9]
Xk+1=Xk+N(Xk)+βI－1h(Xk)+β(Xk－Xr)
式中，先验信息迭代初值参考文献[9]，位置参数的先验信息采用正六边形的几何中心，即
Xr=[0 0 17.5 0]
其最后一个元素0为钟差先验信息，正则化因子设为λ=10－4。
图 4给出了3种方法的点位坐标迭代解序列。高斯-牛顿迭代法收敛速度最慢，且在第3步迭代产生了较大的扰动(当最小二乘点位与控制点近似共面时，迭代方程系数矩阵具有较强的病态性，这导致迭代序列不稳定)。封闭牛顿迭代法由于使用了距离函数的二次项信息，其收敛过程稳定，且可精确收敛至非线性最小二乘解。正则化方法收敛最快，但因先验信息存在系统偏差其解明显存在系统误差(相对于非线性最小二乘点位解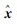
=[4 361.55 4 365.63 143.29]，正则化解[4 350.216 4 353.081 102.497]不满足非线性最小二乘正交条件(22)，两者存在系统偏差[-11.337 -12.548 -40.789])。
|
| 图 4 点位坐标序列 Fig. 4 Sequence of coordinates |
为了验证本文第3部分给出的距离函数线性化误差估计公式，表 3给出了不同点位初值误差(相对于点位坐标非线性最小二乘点位解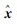=[4 361.55 4 365.63 143.29])所引起的线性化误差。
| m | ||||
| i (距离索引) | Li | ΔxTd″i(x0+αx)Δx (Δx=[100 0 0]) | ΔxTd″i(x0+αx)Δx (Δx=[0 100 0]) | ΔxTd″i(x0+αx)Δx (Δx=[0 0 100]) |
| 1 | 4 923.99 | 2.25 | 0.02 | 2.27 |
| 2 | 3 067.71 | 0.46 | 3.30 | 3.91 |
| 3 | 6 962.62 | 0.03 | 1.51 | 1.55 |
| 4 | 9 975.28 | 0.22 | 0.82 | 1.06 |
| 5 | 10 627.00 | 0.59 | 0.39 | 0.99 |
| 6 | 8 711.36 | 1.11 | 0.10 | 1.22 |
| 累计 | 4.66 | 6.14 | 11.00 | |
结果表明：①距离函数线性化误差与点位初值误差有关，当点位误差方向与观测方向(近似)平行时，线性化误差一般很小，当点位误差方向垂直于观测方向时，一般线性化误差较大。例如，在X方向存在100 m误差时，待定点至第1个控制点方向的距离函数线性化误差约为2.25 m，而待定点至第2个控制点方向的距离函数线性化误差仅为0.46 m，在Y方向存在100 m误差时，待定点至第1个控制点方向的距离函数线性化误差仅为0.02 m，而待定点至第2个控制点方向的距离函数线性化误差为3.30 m；②当控制点(近似)共面时，该平面法向量方向的点位误差对距离函数线性化的影响最大，例如，在Z方向存在100 m误差时，最小线性化误差为0.99 m；③当不同观测方向和点位初值误差方向夹角相差不大时，距离观测越大线性化误差越小，例如，在Z方向存在100 m误差时，观测方向与初值误差方向近似垂直，最大线性化误差发生在第2个距离函数，最小线性化误差发生在第5个距离函数。
5 结 论(1) 距离函数的二阶导数可由其一阶导数表示。本文导出的二阶残余项表达形式简洁，几何意义明确，可用于度量测距定位方程的非线性强度。分析表明，当距离较短或初值精度较低时，二次残余项不容忽视。
(2) 由本文给出的距离函数二阶导数简洁表达式导出的牛顿迭代公式存储和计算成本较低。当距离观测精度较高或测距观测方程的非线性强度较低时，牛顿迭代公式将退化为高斯-牛顿迭代公式。
(3) 当测距定位方程非线性强度很低时，高斯-牛顿迭代法和封闭牛顿迭代法并无显著差异。而对于短距离病态定位方程非线性平差，封闭牛顿迭代公式迭代更稳定、收敛速度更快。
(4) 算例给出的测距定位方程仅附加了钟差参数，附加其他多余参数的应用还有待讨论。
| [1] | YANG Yuanxi,ZHANG Liping. Progress of Geodetic Data Processing for 60 Years in China Part 1:Progress of Functional and Stochastic Model[J]. Geospatial Information, 2009, 7(6):1-5. (杨元喜,张丽萍. 中国大地测量数据处理60年重要进展第一部分:函数模型和随机模型进展[J]. 地理空间信息,2009,7(6): 1-5.) |
| [2] | YANG Yuanxi,ZHANG Liping.Progress of Geodetic Data Processing for 60 Years in China Part 2:Progress of Parameter Estimation Theory and Methodology[J]. Geospatial Information, 2010, 8(1):1-6. (杨元喜,张丽萍. 中国大地测量数据处理60年重要进展第二部分:大地测量参数估计理论与方法的主要进展[J]. 地理空间信息, 2010, 8(1): 1-6.) |
| [3] | ZHENG Zuoya, HAN Xiaodong, HUANG Cheng, et al. Nonlinear Calculation and Precision Analysis of GPS Baseline Vector[J].Acta Geodaetica et Cartographica Sinica, 2004,33(1):27-32. (郑作亚, 韩晓冬, 黄珹, 等. GPS 基线向量的非线性解算及精度分析[J]. 测绘学报, 2004, 33(1): 27-32. ) |
| [4] | LIU Guolin, JIANG Yan, TAO Huaxue. Nonlinear Least Squares Adjustment by Parameters[J].Acta Geodaetica et Cartographica Sinica, 1998,37(3):224-230.(刘国林, 姜岩, 陶华学. 非线性最小二乘参数平差[J]. 测绘学报, 1998,37(3): 224-230.) |
| [5] | TEUNISSEN P J G, KNICKMEYER E H. Nonlinearity and Least-Squares[J]. CISM Journal ACSGC, 1988, 42(4): 321-330. |
| [6] | TEUNISSEN P J G. Nonlinear Inversion of Geodetic and Geophysical Data: Diagnosing Nonlinearity[C]//Proceedings of Developments in Four-Dimensional Geodesy. Berlin Heidelberg: Springer, 1990: 241-264. |
| [7] | LI Fei, HAO Weifeng, WANG Wenrui,et al.The Perturbation Analysis of Nonlinear Ill-conditioned Solution[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):6-9. (李斐, 郝卫峰, 王文睿,等. 非线性病态问题解算的扰动分析[J]. 测绘学报, 2011,40(1): 6-9.) |
| [8] | TEUNISSEN P. First and Second Moments of Nonlinear Least Squares Estimates[J]. Bulletin Geodesy, 1989,63(3): 253-262. |
| [9] | SIROLA N. Closed-form Algorithms in Mobile Positioning: Myths and Misconceptions[C]//Proceedings of Positioning Navigation and Communication, 2010 7th Workshop on IEEE. [S.l.]:IEEE,2010: 38-44. |
| [10] | XUCHU M, WADA M, HASHIMOTO H. Nonlinear Iterative Algorithm for GPS Positioning with Bias Model[C]//Proceedings of the IEEE Intelligent Transportation Systems Conference.Los Alamitos: IEEE, 2004: 684-689. |
| [11] | TANG Limin. Research on the Ill-posed and Solving Methods of Nonlinear Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 630. (唐利民. 非线性最小二乘问题的不适定性及算法研究[J]. 测绘学报, 2012,41(4): 630.) |
| [12] | YAN J C,TIBERIUS G,BELLUSCI G,et al.Feasibility of Gauss-Newton Method for Indoor Positioning[C]//Proceedings of Position, Location and Navigation Symposium, 2008 IEEE/ION. [S.l.]:IEEE, 2008: 660-670. |
| [13] | AWANGE J L, GRAFAREND E W. Explicit Solution of the Overdetermined Three-dimensional Resection Problem[J]. Journal of Geodesy, 2003,76(11-12): 605-616. |
| [14] | JACOBI C. Deformatione et Proprietatibus Determinantum[J]. Journal Reine Angew Math, 1841, 22: 285-318. |
| [15] | KLEUSBERG A, TEUNISSEN P J G.GPS for Geodesy [M]. Berlin: Springer,1996: 176-216. |
| [16] | MADSEN K, NIELSEN H B, TINGLEFF O.Methods for Non-Linear Least Squares Problems [M]. Denmar: Technical University of Denmar,2004:1-20. |
| [17] | AWANGE J L. Algebraic Geodesy and Geoinformatics[M]. Berlin: Springer, 2010;171-192. |
| [18] | GRAFAREND E, SHAN J. Closed-form Solution of P4P or the Three-dimensional Resection Problem in Terms of Mobius Barycentric Coordinates[J]. Journal of Geodesy, 1997,71(3):217-231. |
| [19] | XUE Shuqiang, DANG Yamin, ZHANG Chuanyin. Research on Setting 3D Network of Underwater DGPS[J].Science of Surveying and Mapping, 2006, 31(4):23-24. (薛树强, 党亚民, 章传银. 差分水下GPS定位空间网的布设研究[J]. 测绘科学, 2006,31(4): 23-24.) |
| [20] | DANG Yamin, XUE Shuqiang. A New Newton-type Iterative Formula for Over-determined Distance Equations[C]//Proceedings of Joint IAG Assembly "Earth on the Edge: Science for a Sustainable Planet". Berlin Heidelberg: Springer,2014:607-615. |
| [21] | XUE Shuqiang, YANG Yuanxi, DANG Yamin. A Closed-form of Newton Method for Solving Over-determined Pseudo-distance Equations[J]. Journal of Geodesy, 2014, 88(5):441-448. |