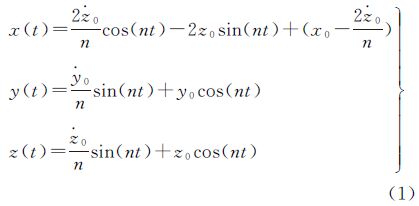2. 武汉大学 测绘学院,湖北 武汉 430079;
3. 中国地震局 地震预测研究所,北京 100036
2. School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;
3. Institute of Earthquake Science,China Earthquake Administration,Beijing 100036,China
1 引 言
21世纪是人类利用卫星跟踪卫星(SST)和卫星重力梯度(SGG)技术提升对地球重力场认知能力的新纪元。地球重力测量卫星CHAMP、GRACE和GOCE的成功发射昭示着人类迎来了一个前所未有的卫星重力探测时代,它们的测量结果直接提供了量化的人为因素和气候变化对全球质量迁移的影响和全球海平面上升的地球物理原因[1, 2, 3, 4, 5]。利用卫星重力测量技术研究地球重力场已经成为目前最具应用前景的高效重力探测手段。
GRACE任务将在3年之内结束,如果后续任务没有及时实施,将不能得到连续的全球质量迁移的观测数据,这对于研究长周期的全球水储量变化和水循环会造成极大的影响。因此,在未来3年之内推出一个卫星重力新任务至关重要,并且其重力场解算精度和时空分辨率至少要达到GRACE任务的程度。同时,随着新的和改进的技术如激光测距、加速度测量、位置感应、微推进力系统的快速发展,新一代重力卫星任务的可行性也进一步增大[6, 7, 8]。
要建立新一代重力卫星任务,就必须清楚地认识现有任务中的不足之处并加以改善。目前GRACE任务的限制之处主要在时空频率混叠、空间分辨率不足以及重力场精度各向异性等3个方面。针对这些问题,国内外相关领域专家提出并研究了多种解决办法[9, 10, 11, 12, 13, 14, 15],主要是优化仪器设备及数据处理方法和利用卫星编队两种,并且目前采用卫星编队来反演地球重力场已成为新一代重力卫星任务的研究热点。本文在此背景下,详细研究了利用不同卫星编队来反演地球重力场的理论方法,为新一代重力卫星任务的实施提供参考。
2 卫星编队设计研究编队卫星的飞行时,将其中一颗卫星称为参考星,其他卫星称为环绕星,通常研究的是环绕星绕参考星的相对运动,描述这种运动在相对运动轨道坐标系Oxyz中进行,坐标原点为参考星质心,x轴在卫星运行轨道面内沿速度方向,y轴指向卫星轨道面的正法线方向,z轴与x、y轴形成右手系。
目前研究编队卫星的相对运动大多数都基于Clohessy-Wiltshire方程(简称C-W方程,也称为Hill方程)或者在此基础上进行修正[16, 17]。C-W方程是基于圆参考轨道、线性化相对运动、除二体引力外无其他摄动和编队中各卫星具有相同轨道周期这几个假设条件推导的一组线性化、常系数的微分方程组[18, 19]。式(1)即C-W方程的解析解,表示了编队卫星在相对运动坐标系中的相对运动状态,其中x0、y0、z0和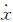 0、
0、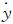 0、Ż0表示编队卫星的初始相对位置和速度,即环绕卫星在相对运动坐标系中的位置和速度。根据其初值的设定,可以得到各种构形的卫星编队
0、Ż0表示编队卫星的初始相对位置和速度,即环绕卫星在相对运动坐标系中的位置和速度。根据其初值的设定,可以得到各种构形的卫星编队
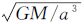 。由式(1)得到包含不同方向观测量的几种适合于重力卫星任务的编队构形:
2.1 串联编队(GRACE-type)
。由式(1)得到包含不同方向观测量的几种适合于重力卫星任务的编队构形:
2.1 串联编队(GRACE-type)编队的初始相对运动状态为
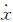 0=
0=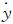 0=Ż0=0
0=Ż0=0编队的初始相对运动状态为
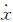 0=
0=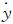 0=Ż0=0
0=Ż0=0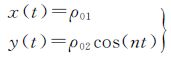
编队的初始相对运动状态为
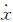 0=-2nz0
0=-2nz0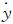 0=Ż0=0
0=Ż0=0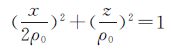
将串联编队和钟摆编队放在同一个编队中就得到了这种卫星编队,其初始相对运动状态和相对运动方程也同时包含了上述两种卫星编队。
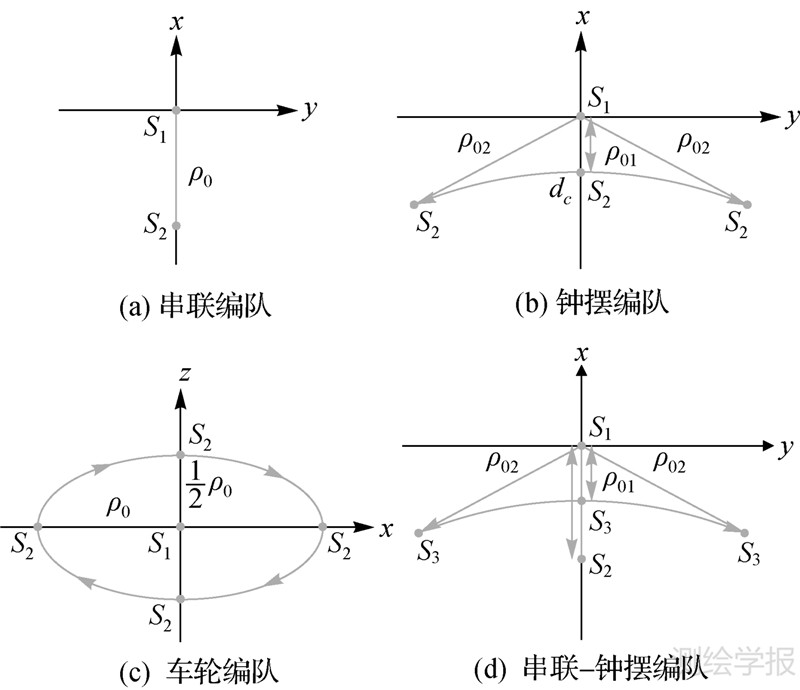
图 1给出了几种卫星编队的相对运动状态示意图,图中以S1卫星为参考星,S2卫星为环绕星构成卫星编队。从其相对运动方程可以知道,钟摆编队中环绕星与参考星的相对运动可以分解为沿x方向的直线运动和沿y方向的简谐运动;车轮编队中环绕星S2围绕参考星S1作长短半轴比为2∶1的椭圆相对运动,这种相对运动发生在xOz平面上,根据相对运动的径向距离最大值出现的方向,可将车轮编队分为东西径向车轮编队(e-w-Cartwheel-type)和南北径向车轮编队(n-s-Cartwheel-type),后文中将深入探讨这两种车轮编队。
|
| 图 1 各种卫星编队相对运动分解示意图 Fig. 1 The relative motion of the proposed satellite formations |
从卫星轨道的重复周期出发,尽量选择轨道重复周期较长的初始轨道参数[20],本文的各种卫星编队的初始轨道高度选择为350 km,轨道倾角89°,星间距离为50~100 km。各卫星编队的初始轨道参数见表 1。
| 轨道参数 | GRACE-type | Pendulum-type | |||||
| GRACE A | GRACE B | difference | Pen. A | Pen. B | difference | ||
| a/km | 6 728.137 | 6 728.137 | Δa=0.0 | 6 728.137 | 6 728.137 | Δa=0.0 | |
| e | 0.001 | 0.001 | Δe=0.0 | 0.001 | 0.001 | Δe=0.0 | |
| i/(°) | 89.0 | 89.0 | Δi=0.0 | 89.0 | 89.0 | Δi=0.0 | |
| Ω/(°) | 0.0 | 0.0 | ΔΩ=0.0 | 0.0 | 0.75 | ΔΩ=0.75 | |
| ω/(°) | 0.0 | 0.45 | Δω=0.45 | 0.0 | 0.0 | Δω=0.0 | |
| M/(°) | 0.0 | 0.4 | ΔM=0.4 | 0.0 | 0.4 | ΔM=0.4 | |
| 轨道参数 | Cartwheel-type | |||||
| Cartwheel 1东西径向 | Cartwheel 2南北径向 | difference | ||||
| R.w.1A | R.w.1B | R.w.2A | R.w.2B | |||
| a/km | 6 728.137 | 6 728.137 | 6 728.137 | 6 728.137 | Δa=0.0 | |
| e | 0.003 7 | 0.003 7 | 0.003 7 | 0.003 7 | Δe=0.0 | |
| i/(°) | 89.0 | 89.0 | 89.0 | 89.0 | Δi=0.0 | |
| Ω/(°) | 0.0 | 0.0 | 0.0 | 0.0 | ΔΩ=0.0 | |
| ω/(°) | 0.0 | -180 | 270 | 90 | Δω=180 | |
| M/(°) | 90 | -90 | 90 | -90 | ΔM=180 | |
表 1中带下划线的数据体现了各卫星编队初始轨道根数的差异,GRACE-type编队中,两颗卫星除了近地点角距ω和平近点角M不同,其他轨道参数均取为相同。理论上讲,共面的GRACE-type卫星编队仅仅需要在平近点角M的设置上有所不同即可,但是通过仿真实验发现,仅仅在平近点角有差异的两颗卫星,其星间距离在长时间内不能很好的保持在100 km,会有一个线性的减小的趋势。为保证两颗卫星较长时间内的星间距离能稳定保持在100 km左右,本文GRACE B卫星的初值是由第1颗卫星的轨道内插而得到,当第1颗卫星运行100 km时,此刻的ω和M即为第2颗卫星的初始值,这样的初值选取可以很好的维持星间距离的稳定性。
Pendulum-type编队的两颗卫星运行在不同的轨道平面上,升交点赤经略有不同,使得星间距离在赤道处达到最大,在极点处达到最小,此处Ω值通过计算得到,使得初始时刻的星间距离能保持在100 km。选取不同的M值是为了使得星间距离在极点最小处不要过小,影响重力场反演的精度,同时使测量值中也可以包含部分沿轨方向观测量。
Cartwheel-type的卫星编队中,两颗卫星除了近地点角距ω和平近点角M不同,其他轨道根数均相同,其中ω和M的差异为π。一颗星的远地点和另一颗星的近地点的距离为这两颗卫星在径向方向的最大距离,而沿轨方向的最大距离是径向距离的两倍。通过径向距离最大的位置设置不同而得到东西径向和南北径向的Cartwheel-type编队。
GRACE-Pendulum-type编队则是由GRACE-type编队的两颗星和Pendulum-type编队的B星这3颗卫星组成,其初始轨道根数的差异也可以从表 1得到。值得注意的是,本文仿真中仅关注两组:GRACE A—GRACE B之间与GRACE A—Pen.B之间的星间距离测量值。
初始轨道参数选定后,即可进行重力场反演仿真实验。本文的仿真平台均基于武汉大学自主研发的动力法定轨和地球重力场反演软件。数据仿真包括轨道数据和星间观测数据,使用EIGEN-05C模型进行仿真,积分得到1组轨道数据和卫卫跟踪数据SST(这里使用的是星间距离变率数据),加入一定量级的误差(轨道误差1 cm,星间变率误差10-7m/s),将其作为真实观测量。其中EIGEN-05C模型在计算中均选用和最终所反演的重力场相同的阶次。求解过程中选择EGM96为参考重力场模型,计算观测量的残差,通过迭代由最小二乘估计卫星的初始状态向量、动力学力模型参数和观测模型中的其他待定参数,将最后估计得到的模型和真实模型做差,并转化为大地水准面来表示目前误差条件下反演模型的精度。这里的反演过程中并未考虑时变信号的影响,所有卫星编队构形的数据模拟周期均为30 d、10 s一个采样。
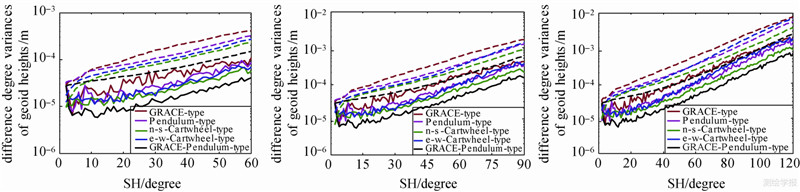
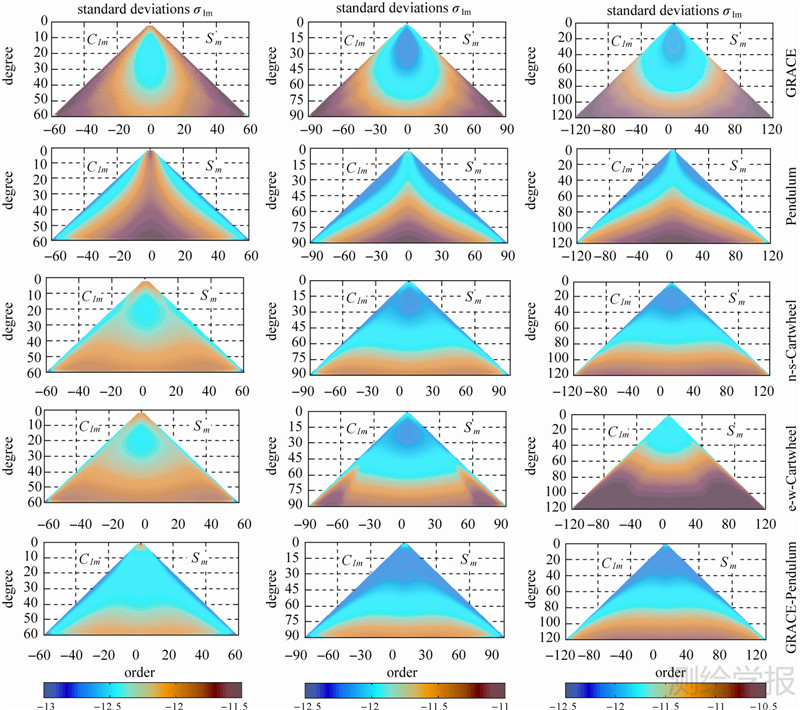
3.2 仿真结果分析为了更好地比较和解释各种卫星编队对重力场不同波长的反演能力,模型的最高阶分别截断到了60阶、90阶和120阶。图 2给出了在不同编队模式下,解算的重力场模型与真实模型的大地水准面误差的阶RMS(实线)及累计误差阶RMS(点线),表 2给出了不同卫星编队解算的重力场模型与真实模型的大地水准面阶误差统计,图 3则给出了各阶次重力场系数的误差分布情况,图中的色标是表示取常用对数所得的值。
|
| 图 2 不同卫星编队解算的重力场模型与真实模型的大地水准面阶误差变化及累计误差变化 Fig. 2 Static gravity field solutions of formation at different degrees,left:n=60,middle:n=90 and right:n=120.Solid lines represent degree variances of geoidal height differences between EIGEN-05C and the gravity solutions,dashed ones represent the cumulative geoid errors |
| mm | |||||||||||
| 编队类型 | n=60 | n=90 | n=120 | ||||||||
| RMS | 最小值 | 最大值 | RMS | 最小值 | 最大值 | RMS | 最小值 | 最大值 | |||
| GRACE-type | 0.371 | -2.006 | 1.944 | 1.477 | -7.104 | 7.658 | 6.633 | -41.971 | 36.951 | ||
| Pendulum-type | 0.333 | -1.399 | 1.426 | 1.142 | -5.231 | 5.489 | 4.977 | -27.102 | 23.603 | ||
| n-s-Cartwheel-type | 0.211 | -0.959 | 1.058 | 0.789 | -3.879 | 4.436 | 3.317 | -21.692 | 17.946 | ||
| e-w-Cartwheel-type | 0.243 | -1.049 | 1.629 | 1.173 | -8.203 | 9.280 | 6.058 | -45.090 | 41.841 | ||
| GRACE-Pendulum-type | 0.140 | -0.543 | 0.629 | 0.529 | -2.405 | 2.466 | 2.295 | -10.828 | 9.823 | ||
|
| 图 3 卫星编队反演重力场球谐系数的方差分布图 Fig. 3 Error spectra of spherical harmonic coefficients of formation at different degrees,left:n=60,middle:n=90 and right:n=120 |
从表 1所统计的大地水准面阶误差可以知道,GRACE-Pendulum-type编队解的RMS值最小,n-s-Cartwheel-type编队次之,并且随着解算阶次的增加,各种卫星编队对于重力场反演的精度也在提高,与GRACE-type编队相比,幅度可达9%~65%,可见利用卫星编队来反演重力场对其精度的提高有很大好处。
图 2和图 3给出了详细的解算结果信息。在本文所探讨的5种卫星编队中,无论从误差阶RMS还是重力场系数的误差谱图上来看,由3颗卫星组成的GRACE-Pendulum-type编队都能够得到最好的结果,这说明增加卫星数目和多方向可以显著地提高卫星任务观测量的时空分辨率和地球重力场的反演精度,但是这种构形将增大任务的耗资。
在仅有两颗卫星组成的卫星编队中,GRACE-type编队只包含沿轨方向观测量,Pendulum-type编队同时包含沿轨方向和法向观测量,而Cartwheel-type编队有沿轨方向和径向观测量,从仿真结果来看,GRACE-type编队的重力场解算结果最差,其他两种编队的结果在全阶次上优于这种编队构形,这说明多方向的观测量有利于重力场解算精度的提高;同时,Cartwheel-type编队的重力场解算结果又较Pendulum-type编队稍好,这说明径向观测量是重力场信息的主要来源;而随着解算阶次的增大,可以看到南北径向的观测量对于高阶重力场解算效果更好,到120阶的重力场解算时,其精度远远高于其他几种两颗卫星构形的编队,仅稍次于由3颗卫星构成的GRACE-Pendulum-type编队。
从系数的误差谱图上可以看出,Cartwheel-type编队的重力场解算结果误差趋于各向同性,而GRACE-type编队和Pendulum-type编队则表现出各向异性的敏感度,造成这种现象的原因在于,车轮编队中均匀的包含了沿轨和径向两个方向的观测量,而串联编队只包含一个方向(沿轨方向)观测量,钟摆编队则由于轨道设计时,为了保证星间距离在50~100 km之间,两颗卫星连线与赤道的夹角非常小,使得其星间观测量中法向观测量占优,湮没了沿轨方向观测量的贡献。由此可以看出,单一的沿轨方向和法向重力观测量是导致重力场各向异性敏感度的重要原因,而径向的观测量和均匀的多方向观测量联合可以大大削弱这种影响。
对于Cartwheel-type的两种卫星编队来说,误差谱图相对变化较大,当n=60时,这两种卫星编队的重力场解算系数误差谱图几乎一样,随着解算阶次的增加,从60阶开始,e-w-Cartwheel-type编队的扇谐和田谐系数误差急剧增大,尤其是80~120阶次部分,其误差较其他编队类型几乎有了数量级的增加,这极大地影响了最终重力场解算精度。分析造成这种现象的原因,是由于东西径向Cartwheel-type编队的径向最大距离出现在赤道区域,受地球扁率的影响较大,其星间距离在一个月内的变化不如南北方向的径向Cartwheel-type编队稳定,从而导致其星下点轨迹产生较大变化,并且这种变化导致观测量对于重力场的细部信息不敏感,尤其是对高阶扇谐和田谐系数的反演造成了较大的误差。
其他各卫星编队的重力场系数的误差则基本延续了60阶、90阶的趋势,可见这些编队对于重力场反演来说较为稳定,尤其是n-s-Cartwheel-type编队,构形稳定且适合高阶重力场解算,它不仅可以得到极为均匀的全球误差分布和几乎各向同性的重力场解算结果,并且由于只包含两颗卫星,花费也较GRACE-Pendulum-type编队少,是一种极具性价比的卫星编队方式。
从重力场系数的误差谱图还可以知道,沿轨方向观测量对扇谐系数反演能力最差,而法向观测量会影响带谐项系数的反演精度,径向观测量和多方向联合的观测量能得到接近各向同性敏感度的重力场系数分布。
4 结果与讨论本文研究了适合于重力场反演任务的几种卫星编队构形,通过仿真试验,详细分析了各种卫星编队探测重力场的能力和优势,可以得到以下几点结论:
(1) 与GRACE-type相比,其他几种卫星编队都可不同程度的提高重力场解算精度,幅度可达9%~65%。
(2) 沿轨方向和法向的单一观测量是导致重力场各向异性敏感度的重要原因,而径向的观测量和均匀的多方向观测量联合可以大大削弱这种影响,为重力场解算提供最好的条件,有利于重力场解算精度的提高。
(3) 沿轨方向观测量对扇谐系数反演能力最差,法向观测量会影响带谐项系数的反演精度,径向观测量和多方向联合的观测量能得到较好的接近各向同性敏感度的重力场系数分布。这一结论从一个新的角度为进行特定卫星任务设计提供了重要参考。
(4) 径向观测量是重力场信息的主要来源,并且随着解算阶次的增大,由于地球扁率对其轨道的影响,东西径向的车轮编队已经不适合于高阶重力场的解算,而南北径向的车轮编队则非常稳定,对于高阶重力场解算效果好,是较为经济实用的一种卫星编队模式。
基于以上结论,在进行新一代重力卫星任务设计时,可以考虑具有多方向观测量,尤其是南北径向观测量的卫星编队,以得到高精度、高时空分辨率及各向同性的重力场解算结果,能够为研究全球质量迁移提供更好的条件。
| [1] | TAPLEY B D, RIES J, BETTADPUR S, et al. GGM02-An Improved Earth Gravity Field Model from GRACE [J].Journal of Geodesy, 2005, 79(8):467-478. |
| [2] | CHEN J L,WILSON C R,TEPLEY B D. Satellite Gravity Measurements Confirm Accelerated Melting of Greenland Ice Sheet [J]. Science, 2006, 313(5795):1958-1960. |
| [3] | FÖRSTE C, SCHMIDT R, STUBENVOLL R et al.The GeoForschungsZentrum Potsdam/ Groupe de Recherche de Gèodésie Spatiale Satellite-only and Combined Gravity Field Models: EIGEN-GL04S1 and EIGEN-GL04C [J].Journal of Geodesy,2008, 82(6):331-346. |
| [4] | CHEN J L,WILSON C R, SWO K W. Optimized Smoothing of Gravity Recovery and Climate Experiment (GRACE)Time-variable Gravity Observations [J]. Journal of Geophysical Research, 2006, 111(B06): 408-418. |
| [5] | LI J C, ZHANG S J, ZOU X C,et al. Precise Orbit Determination for GRACE with Zero-difference Kinematic Method [J]. Chinese Sci Bull, 2009, 54(16), 2355-2362. (李建成,张守建,邹贤才,等.GRACE卫星非差运动学厘米级定轨[J].科学通报, 2009, 54(16): 2355 -2362.) |
| [6] | BENDER P,HALL J L,YE J, et al.Satellite-satellite Laser Links for Future Gravity Missions [J]. Space Science Reviews, 2003, 108(1-2): 377-384. |
| [7] | SHEARD B S,HEINZEL G,DANZMANN K, Intersatellite Laser Ranging Instrument for the GRACE Follow-on mission [J]. Journal of Geodesy 2012, 86(12): 1083-1095. |
| [8] | FLURY J, BETTADPUR S, TAPLEY B. Precise Accelerometry Onboard the GRACE Gravity Field Satellite Mission [J].Advances in Space Research 2008,42(8):1414-1423. |
| [9] | ELSAKA B. Simulated Satellite Formation Flights for Detecting Temporal Variations of the Earth’s Gravity Field[D].Bonn: University of Bonn, 2010. |
| [10] | LOOMIS BRYANT D. Simulation Study of a Follow-on Gravity Mission to GRACE [D]. Boulder: University of Colorado, 2009. |
| [11] | WIESE, D N, FOLKNER W M, NEREM R S. Alternative Mission Architectures for a Gravity Recovery Satellite Mission [J]. Journal of Geodesy, 2009, 83(6): 569-581. |
| [12] | BENDER P,WIESE D N,NEREM R S. A Possible Dual-GRACE Mission with 90 Degree and 63 Degree Inclination Orbits [C]//Proceedings of 3rd International Symposium on Formation Flying, Missions and Technologies.Noordwijk:[s.n.],2008. |
| [13] | SNEEUW N, SCHAUB H. Satellite Clusters for Future Gravity Field Missions [C]//Gravity, Geoid and Space Missions.Berlin/Heidelberg:Springer,2005. |
| [14] | SNEEUW N, FLURY J, RUMMEL R. Science Requirements on Future Missions and Simulated Mission Scenarios [J]. Earth, Moon and Planets, 2004, 94(1-2):113-142. |
| [15] | EINARSSON I. Sensitivity Analysis for Future Gravity Satellite Missions [D]. Potsdam: Deutsches GeoForschungs-Zentrum GFZ, 2011. |
| [16] | CLOHESSY W H,WILTSHIRE R S. Terminal Guidance System for Satellite Rendezvous [J]. Journal of the Aerospace Sciences, 1960, 27(5F):653-674. |
| [17] | HILL G W. Researches in the Lunar Theory [J]. American Journal of Mathematics, 1878, 1(1):5-26. |
| [18] | CHEN Jie, ZHOU Mengqing, LI Chunsheng. Research on the Orbit Design Method for Satellite Formation of Distributed SAR Micro-satellite [J]. Science in China:Series E, 2004, 34(6);654-662. (陈杰,周荫清,李春升.分布式SAR小卫星编队轨道设计方法研究[J].中国科学:E辑, 2004, 34(6): 654-662.) |
| [19] | LI Junfeng, XUE Dan. Review of Relative Motion Description Methods for Satellite Formation Flying [J]. Journal of Astronautics, 2008, 29(6):1689 -1694. (李俊峰,雪丹. 编队卫星相对运动描述方法综述[J]. 宇航学报, 2008, 29(6):1689-1694.) |
| [20] | ZHAO Qian, JIANG Weiping, XU Xinyu, et al. Research on the Design of LEO Repetition Period and Its Influence on Gravity Field Research [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):191-195,202. (赵倩,姜卫平,徐新禹,邹贤才. 低轨道卫星重复周期的设计方法及其对重力场反演的影响[J].测绘学报, 2013, 42(2): 191-195,202.) |