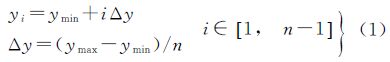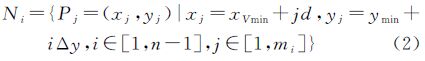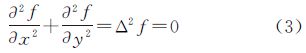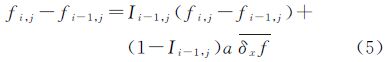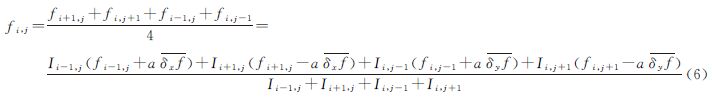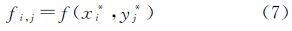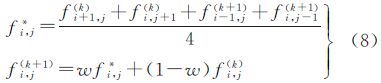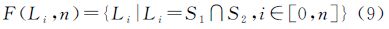2. 海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连 116018;
3. 海军海洋测绘研究所,天津 300061
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA,Dalian Naval Academy,Dalian 116018,China;
3. Naval Institute of Hydrographic Surveying and Charting,Tianjin 300061,China
1 引 言
低潮线是指海水在海岸上退落的最低线界[1, 2],在海洋划界、海岸工程建设和滩涂资源管理等应用中具有重要意义。根据《联合国海洋法公约》,沿岸低潮线是领海基线及基点确定的重要一环[3, 4],其位置的准确与否对海洋划界具有直接影响。此外,低潮线的位置及长度也是海岸带调查中最基础的数据之一,其对滩涂面积计算分析等具有重要意义[1]。
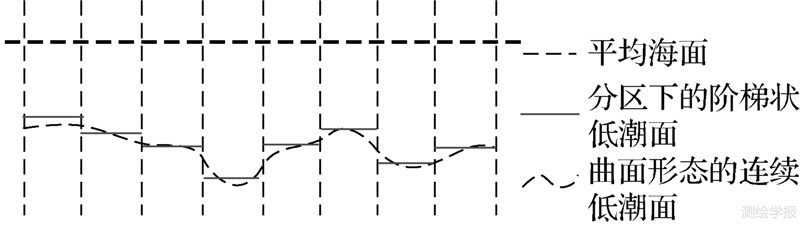
如何提取较高精度的沿岸低潮线,一直是海洋划界、平缓滩涂监测等领域面临的难题[5, 6]。低潮线提取主要有3种方法:①实地测量方法;②基于影像水边线的推算方法;③基于潮滩DEM和低潮面模型的简单求交方法。实地测量方法是利用测量仪器在低潮线附近每隔一定距离采集特征点,标记在数字地形图上并连接成低潮线。该方法必须进行大量野外工作,效率低[1, 6, 7],而且,由于低潮线并无明显标记,实际中也很难测到其准确位置;基于影像水边线的推算方法,首先基于影像数据提取出瞬时水位线[8, 9, 10],然后对水位线进行潮位校正得到低潮线,但当前的推算做法基本上都假定潮滩地形是规则的斜坡[11, 12],这明显不适用于地形起伏较大的区域;简单求交方法根据潮汐模型计算当地低潮面(深度基准面)的高程,以此高程面与潮滩DEM横切,采用等值线追踪等技术得到低潮线[1, 11, 12, 13, 14]。该方法所需人工干预少,在小范围区域内提取低潮线效果相对较好,目前得到了较为广泛的应用。然而,该方法在提取低潮线时将低潮面简化为平面处理,而事实上,对于范围较大的沿岸区域,特别是潮汐变化差异较大时,沿岸低潮面是一个曲面而不是简单的平面,由此会引起低潮线提取的较大偏差。尽管实践中也可以采用分区提取低潮线再进行拼接的方法,但这种方法很难得到最合理的分区,若分区粗略,会使区域内的低潮面呈不连续的阶梯状分布(如图 1所示),不足以充分反映区域内的潮汐变化差异,可能导致低潮线提取精度不高及不连续现象;若分区较细,虽然能保证低潮线精度,但分区及低潮线拼接等处理复杂。
|
| 图 1 分区提取低潮线示意图 Fig. 1 The sketch map of the low tidal line partition extraction |
针对以上问题,本文提出一种基于曲面求交的低潮线提取方法。首先采用单向分区策略构建潮滩数字高程模型,然后将低潮面视为曲面进行处理,构建沿岸网格低潮面模型,表达曲面形态的沿岸低潮面,最后,对所构的两个网格模型进行曲面求交,提取沿岸低潮线。
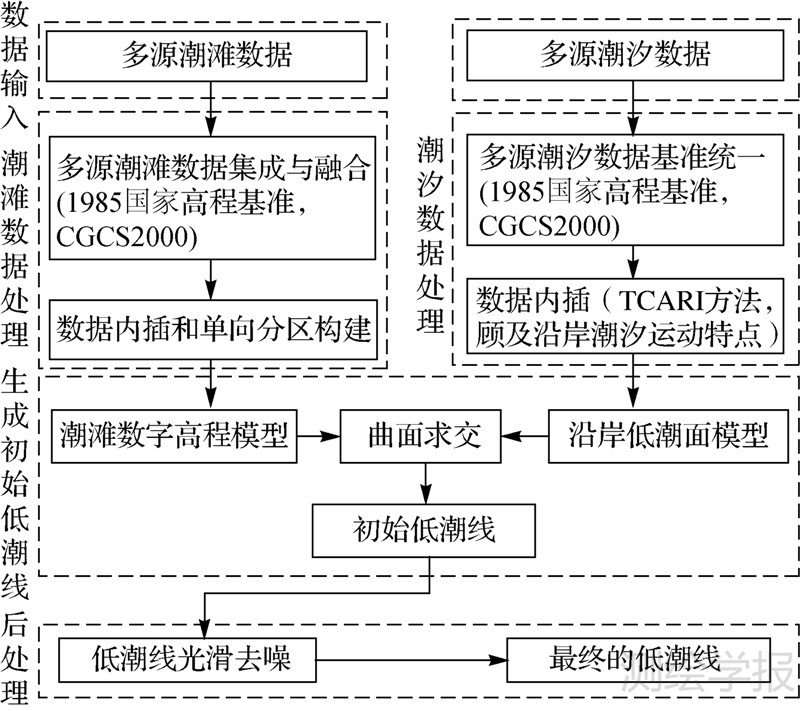
2 基于曲面求交的低潮线提取方法潮滩数字高程模型的构建需要利用多源潮滩数据,而沿岸网格低潮面模型的构建需要利用已有的沿岸低潮面数据,为完成曲面求交处理,需要将不同源数据统一到同一基准,本文数据平面基准采用CGCS2000坐标系统,垂直基准采用1985国家高程基准。基于曲面求交的低潮线提取方法的基本思路如图 2所示。
|
| 图 2 基于曲面求交的低潮线提取方法流程图 Fig. 2 The flow chart of low tidal line extraction based on mesh surface intersection |
潮滩数据来源复杂多样,需要进行多源潮滩数据的集成与融合,将数据统一到CGCS2000坐标系统和1985国家高程基准,潮滩DEM结构选择三角网,建模的基本方法采用逐点插入法。
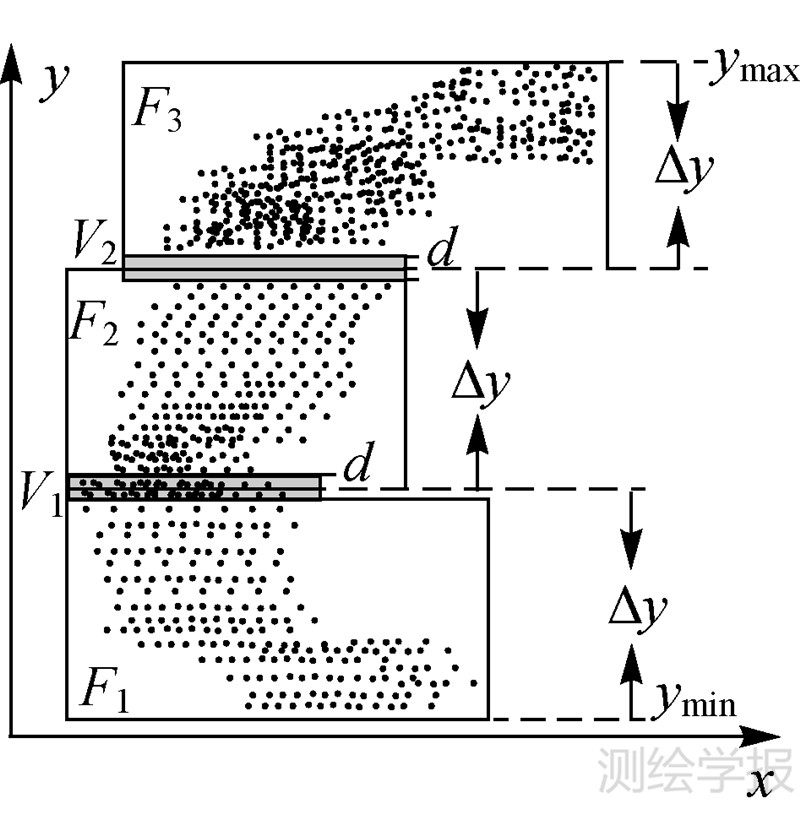
从大范围潮滩数据呈现狭长带状分布的特点出发,为优化潮滩模型的构建和方便曲面求交及拼接,提高整体建模效率,在构建潮滩DEM时采用基于分割线的单向分区策略(如图 3所示)。具体步骤如下:
(1) 按照潮滩数据分布的总体趋势确定分区方向(以按Y轴方向分割为例),然后确定分区数目和各分区的数据范围及分割线的y坐标。根据数据范围,给定合适的分区数n,则存在n-1条分割线,其y坐标计算公式为
式中,Δy表示分区距离;ymin、ymax表示点集S在Y轴方向的最小值和最大值。(2) 建立分割线缓冲区V(如图 3中的阴影区)。以分割线为中心线构建缓冲区,缓冲距h可以设为源数据间距的若干倍;将位于缓冲区的点存入分割线类中,并确定分割线缓冲区的x值范围[xvmin,xvmax]。通过构建分割线缓冲区,可以提高共公边界点的确定速度。
(3) 构建相邻分区的公共边界,即计算分割线上新加点的坐标。根据源数据密度确定合适的间距d,确定分割线上新加点的数目及x坐标。则分割线i的新加点集Ni为
式中,mi=(xVmax-xVmin)/d,表示分割线上新加点的数目。新加点的高程值z可以通过内插法计算获得。内插计算时,在分割线缓冲区内搜索离散点,采用反距离加权等插值方法进行计算,这样可以保证新加点的精度、密度与原始数据基本相符。
(4)分区构建TIN-DEM及各分区TIN-DEM的合并。基于分割线的单向分区策略,充分利用潮滩数据狭长带状分布的特点,通过构建相邻分区的公共边界使相邻分区TIN-DEM可以直接拼接成整体TIN-DEM,避免了传统方法在分块拼接时需要搜索子网边界公共切线及三角网拓扑关系重构[15, 16, 17]。在进行曲面求交提取沿岸低潮线时,通过该方法构建分区DEM,分别进行曲面求交,然后由分区低潮线拼接组成整体低潮线。由于相邻分区之间具有公共边,因此,分区低潮线可以直接相连组成整体低潮线。
|
| 图 3 潮滩数据分区示意图 Fig. 3 The sketch map of a regionalization strategy |
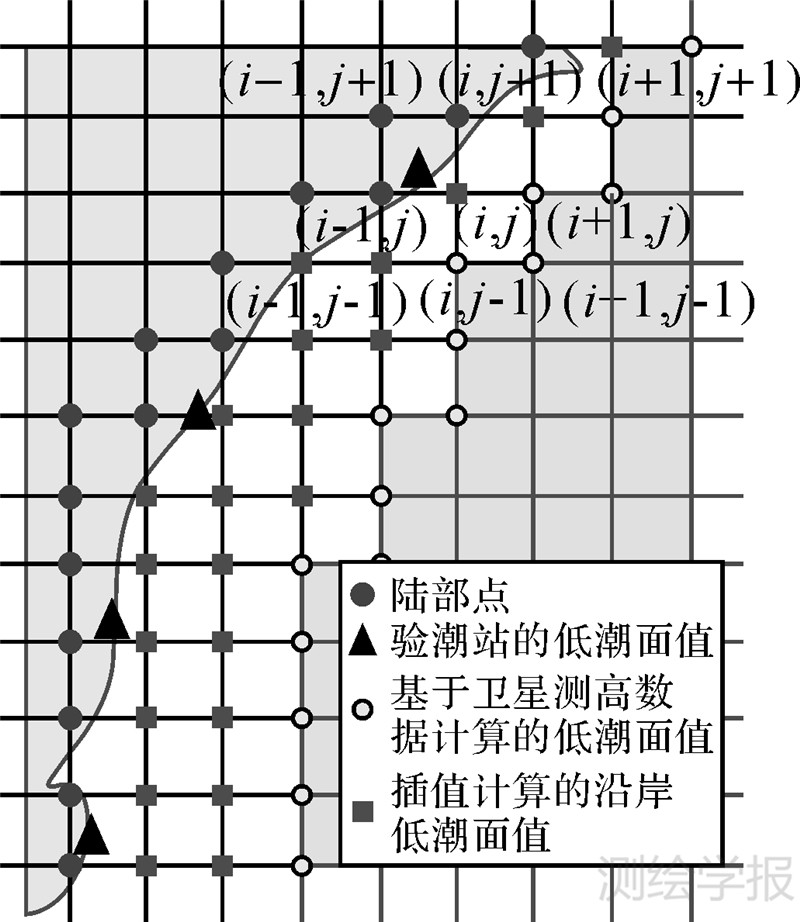
针对常用低潮面模型在较大范围区域内呈阶梯状断续分布的不足,为实现曲面求交提取低潮线,需要构建连续、曲面形态的沿岸低潮面模型。虽然结合卫星测高数据和潮汐动力学方程,可以构建曲面形态的低潮面模型[18],但沿岸海域潮波传播复杂,该方法构建的低潮面模型在沿岸海域精度可能不高,且可能存在不少的无效网格点。若单纯地利用外推法估计无效网格点的低潮面值,在某些区域可能会产生较大误差。为此,本文借鉴文献[19]提出的TCARI方法,顾及边界条件约束,综合利用沿岸验潮站和网格潮汐模型数据信息(低潮面源数据利用调和方法或潮位传递模型计算获得),采用拉普拉斯插值构建精度更高的曲面形态的沿岸网格低潮面模型(如图 4所示)。具体思路如下:
在不考虑海底摩擦力等物理作用的情况下,可以认为潮汐变化f满足拉普拉斯方程,即
对于该拉普拉斯方程的求解,满足数值边界条件和自然边界条件,即
式中,(xm,ym,Fm)表示验潮站位置坐标和低潮面值;n表示海岸线法向量;a为边界条件调控系数(一般取0.9)。式(4b)表明方程的自然边界条件是邻域导数的平均值。式(4b)可以用差分方式近似表示,即对网格区域的任意节点
式中,fi,j、fi-1,j分别表示网格点(xi,yj)、(xi-1,yj)对应的低潮面值;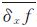 表示f在x方向的导数平均值;Ii-1,j为海陆标志,当点(xi-1,yj)处于海部,Ii-1,j=1,当点(xi-1,yj)处于陆部,Ii-1,j=0。
表示f在x方向的导数平均值;Ii-1,j为海陆标志,当点(xi-1,yj)处于海部,Ii-1,j=1,当点(xi-1,yj)处于陆部,Ii-1,j=0。
对于任一内节点(xi,yj),由式(4)、式(5)得到拉普拉斯方程的五点格式的有限差分解
式中,fi,j、fi+1,j、fi-1,j、fi,j+1、fi,j-1分别是对应网格点的低潮面值。由于海岸线是不规则的,海岸线法向量方向不易确定,可以用点(xi,yj)邻域(3×3)内的一阶导数平均值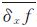 、
、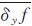 近似代替。
近似代替。
对于边界节点(xi,yj),取与该点邻域范围内最临近的采样点(xi*,yj*)的值作为近似解,即
采用超松弛迭代法求解上述方程,迭代式为
式中,w为超松弛因子,满足1<w<2。当满足max|(fi,j(k)-fi,j(k-1))|<ε时,迭代结束(ε=10-6)。通过上述过程,计算出每个网格点的低潮面值,从而构建起网格曲面形态的沿岸低潮面模型。
|
| 图 4 基于TCARI方法的沿岸低潮面模型构建 Fig. 4 The coastal low water model construction based on TCARI |
本文构建的潮滩数字高程模型和沿岸低潮面模型分别采用三角网和规则格网,由于规则格网可以转化成三角网,两模型的曲面求交的核心问题是两三角网格曲面的求交问题。设两三角网格曲面分别为S1和S2,则曲面求交为求如下集合
式中,F(Li,n)表示交线集合;Li表示两曲面的一条交线;n表示交线数量。当F(Li,n)≠∅时,表示两三角网格曲面相交于n条曲线。关于三角网格曲面求交,已有学者进行了研究[20, 21]。本文在已有算法的基础上,结合潮滩数字高程模型和沿岸低潮面模型的特点,采用以下策略对两三角网格曲面求交进行优化。具体步骤如下:
(1) 建立三角网格曲面的层次包围盒,优化曲面的碰撞检测,如图 5(a)所示。层次包围盒的构造过程为:
① 构造初始包围盒B0=B1∩B2,B1、B2分别是两个三角网格曲面的轴向包围盒。
② 确定两个曲面中与初始包围盒B0相交的三角形集合SB1、SB2。
③ 根据三角网格曲面的三角形数量,确定包围盒剖分层次(顾及算法效率,剖分层次根据经验选择5层),对初始包围盒B0进行剖分,得到子包围盒Bi。
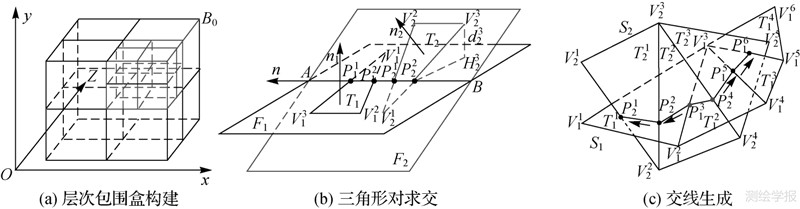
|
| 图 5 三角网格曲面求交示意图 Fig. 5 The sketch map of triangular mesh surface intersection |
(2) 对三角形集合SB1、SB2中的每个三角形,判断是否与子包围盒Bi相交,并记录子包围盒Bi中的三角形;对包含两个曲面的三角形的子包围盒标记为有效子包围盒。
(3) 以子包围盒为单元,对三角形对进行求交判断处理,并求得相交三角形对的交线段,如图 5(b)所示。
采用以下策略进行三角形对的快速求交处理:
① 利用符号距离判断三角形与另一三角形所在平面是否相交,即判断T1∩F2≠&T2∩F1≠∅是否成立。
② 利用区间投影重叠法判断两三角形T1和T2是否相交。首先计算交线向量n=n1×n2及其坐标轴投影(nx,ny,nz),确定最大投影坐标轴k=x,或y,或z轴;其次计算三角形T1边V11V12、V11V13与平面F2的交点和三角形T2边V21V22、V21V23与平面F1的交点在该轴的投影P1,k1、P1,k2、P2,k1、P2,k2。若max(P1,k1,P1,k2)<min(P2,k1,P2,k2) 或max(P2,k1,P2,k2)<min(P1,k1,P1,k2),表明线段P11P12与P21P22无重叠部分,说明两三角形不相交;否则,说明两三角形相交,进行步骤3。
③ 在T1和T2相交的情况下,计算具体的交点坐标,得到两三角形的交线段。
算法通过两步三角形相交测试处理,排除不可能相交的三角形,提高三角形对求交处理的效率。
(4) 利用拓扑关系追踪交线段,完成曲面交线的快速重构,如图 5(c)所示。
三角网格曲面间的交线是由三角形对的交线段所组成的交线链或交线环。而通过步骤1、步骤2求出的三角形对的交线段是散乱无序的,需要对其进行追踪排序形成曲面交线。由于沿着曲面上交线的行进方向,相邻交线段所在的三角形也是相邻的。根据这一特性,利用拓扑关系追踪三角形的邻接三角形,得到三角网格曲面的交线。
图 5(c)中,S1、S2为求交的两个三角网格曲面,三角形T11、T12、T13、T14∈S1,三角形T21、T22、T23∈S2,P21P22、P22P13、P13P24、P24P15、P15P16是计算的三角形对的交线段。其中
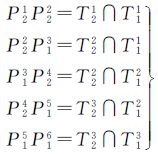
依次对两三角网格曲面的交线段进行追踪,得到最终的曲面交线。
3 试验与分析 3.1 试验数据选择南海某一较大范围沿岸区域的相关数据进行试验验证与分析,试验区域如图 6所示。潮滩高程数据由部分实测数据和相关海图数据集成融合后经过适当内插得到,潮滩DEM三维图如图 7所示。低潮面数据采用区域内的验潮站低潮面数据和基于卫星测高数据构建的网格低潮面数据,边界约束数据采用试验区域内的岸线数据,构建的沿岸低潮面模型网格分辨率为1′。将潮滩数据和低潮面数据统一到同一基准(CGCS2000平面基准,1985国家高程基准)。选择3块局部小范围数据作为一类对比区域,如图 6中A-1、B-1、C-1区域;选择3块较大范围数据作为二类对比区域,如图 6中A-2、B-2、C-2区域。

|
| 图 6 试验区域影像图 Fig. 6 The image of experimental region |
|
| 图 7 试验区域潮滩DEM Fig. 7 The DEM of experimental region |
低潮线并无明显标记,实际中难以测到其准确位置,只能采用对比试验和理论分析的方式对其精度进行评估。为方便叙述,本文提出的基于曲面求交的低潮线提取方法简称曲面求交方法。在试验区域内分别采用曲面求交方法和简单求交方法提取低潮线,并对提取结果进行对比及分析,以验证曲面求交方法提取低潮线的有效性。具体的试验设计思路如下(如图 8所示):
(1) 利用2.1节的潮滩DEM构建方法构建潮滩DEM;利用2.2节的TCARI方法构建沿岸低潮面模型;对潮滩DEM和沿岸低潮面模型进行曲面求交提取出低潮线。
(2) 建立一类对比区域,即小范围对比区域。该类区域是以各验潮站为中心,范围为±2 km的矩形区域,在区域内可以将低潮面认为是一平面。在对比区域内构建局部潮滩DEM,采用简单求交方法提取局部低潮线。
(3) 在一类对比区域内,对潮滩DEM作一系列剖面线(间隔为50 m),求得剖面线与曲面求交方法提取低潮线的交点和剖面线与简单求交方法提取低潮线的交点,计算两交点(即检查点对)之间的距离偏差;计算多个检查点对,得到统计结果。
(4) 建立二类对比区域,即较大范围对比区域;该类区域是以各验潮站为中心,范围为±5 km的矩形区域,模拟分区提取低潮线方法的分区区域。在对比区域内构建局部潮滩DEM,采用简单求交方法提取局部低潮线。
(5) 在二类对比区域内,对潮滩DEM作一系列剖面线(间隔为50 m),求得剖面线与曲面求交方法提取低潮线的交点和剖面线与简单求交方法提取低潮线的交点,计算两交点(即检查点对)之间的距离偏差;计算多个检查点对,得到统计结果。
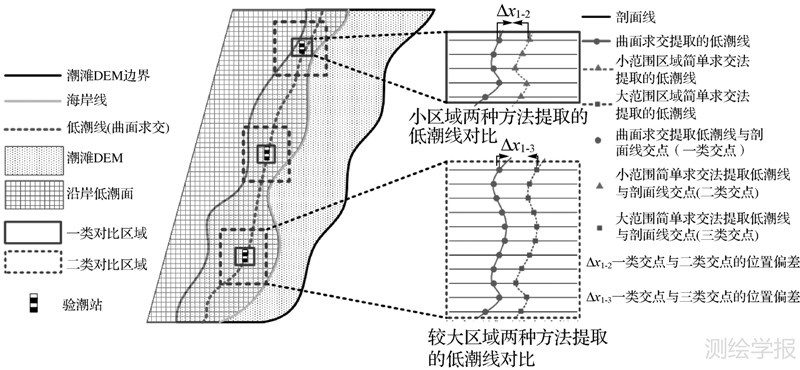
|
| 图 8 试验设计示意图 Fig. 8 The sketch map of experimental design |
分别采用曲面求交方法和简单求交方法提取6块对比区域的低潮线并沿X方向作剖面线,计算两种低潮线与每个剖面线的离散交点对(检查点对)的距离偏差Δx,得出统计结果。表 1列出了两种方法提取的低潮线位置的比较结果,通过结果对比和理论分析,可以进一步说明两种方法提取低潮线的精度差异。表中,平均低潮面差值指检查点对低潮面差值的平均值。
| 对比区域 | 两种方法检查点对的距离差Δx/m | ||||||
| 区域 | 检验点对数 | 平均低潮面差值/m | 最大值max | 平均值Δx | 中误差RMSE | ||
| 一类区域 | A-1 | 71 | -0.006 5 | 7.167 | -0.949 | 1.461 | |
| B-1 | 67 | 0.009 9 | 5.700 | 1.448 | 1.908 | ||
| C-1 | 58 | -0.010 4 | 10.600 | -1.553 | 2.586 | ||
| 二类区域 | A-2 | 264 | 0.043 0 | 131.580 | 12.938 | 21.969 | |
| B-2 | 233 | 0.094 4 | 204.681 | 40.353 | 52.167 | ||
| C-2 | 386 | 0.063 5 | 281.716 | 24.042 | 35.843 | ||
从表 1可以看出,在一类对比区域内,两种方法提取的低潮线偏差平均值和中误差都较小。这表明,在小范围区域内,曲面求交方法与简单求交方法提取的低潮线精度相当。其原因是,在小范围区域内,潮汐变化较小,低潮面可以简化为一个平面,低潮面与潮滩DEM曲面求交转换为平面与DEM求交,即前文提到的简单求交。但如果区域内潮汐变化差异较大,则需要更精细的潮汐模型。从表 1还可以看出,在二类对比区域内,两种方法提取的低潮线偏差的平均值和中误差都较大。这表明,在该类区域内,两种方法提取的低潮线偏差较大。其原因是,该类区域相当于分区提取方法的子分区,在分区范围内,潮汐变化差异仍可能较大(从表中也可以看出,此时低潮面差值较大),简单求交方法将低潮面简化为平面处理,可能不足以充分反映潮汐变化的这种差异,而曲面求交方法通过构建曲面形态的沿岸低潮面模型,并直接对潮滩DEM和低潮面模型进行曲面求交,可以更有效地提取低潮线。
图 9表示低潮线提取结果对比及局部细节图。其中,(A-2)、(B-2)、(C-2)分别表示3个较大范围对比区域内利用两种方法提取的低潮线对比图。可以看出,两种方法提取的低潮线在验潮站附近非常吻合,而在距离验潮站较远的区域偏差较大(如右侧的局部放大图)。这表明,在提取沿岸低潮线时,尤其是大范围区域内,需要构建更为精细的低潮面模型,以充分顾及区域内潮汐变化的差异。
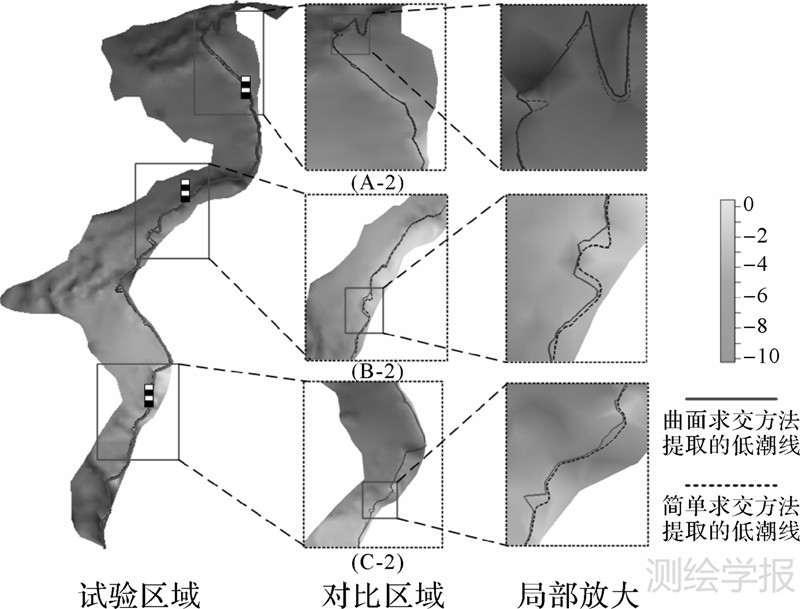
|
| 图 9 低潮线提取结果对比及局部细节图 Fig. 9 The low tidal line extraction and details |
由上述试验和分析可得,当提取低潮线的区域较大时,简单求交方法与曲面求交方法提取的低潮线偏差较大。由于曲面求交方法通过构建曲面形态的沿岸低潮面模型,直接采用曲面求交的方法提取低潮线,相比简单求交方法,更能充分顾及区域内的潮汐变化差异,因此,从理论上分析,曲面求交方法提取的低潮线精度更高。
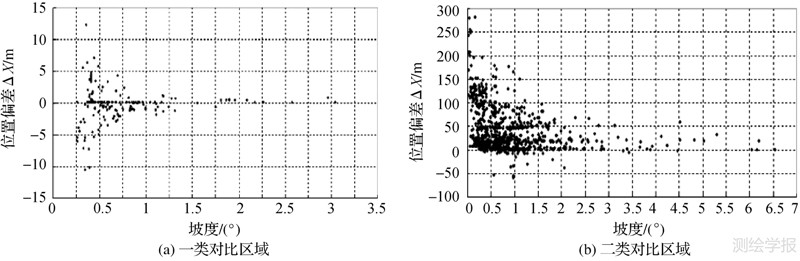
图 10表示检验点邻域坡度与低潮线位置偏差的关系图。从图中可以看出,低潮线位置偏差较大的检验点多分布于地形坡度较小的区域,而坡度较大区域的低潮线位置偏差较小。这表明,低潮线提取精度与地形坡度有密切关系,地形坡度较小的区域,提取的低潮线精度较差。其主要原因是,低潮面模型在垂直方向的误差,通过一定方式转化成水平位置误差,坡度越小,偏差的放大效应越明显。因此,对于地形平坦区域的低潮线提取,需要格外重视沿岸低潮面模型的精度。
|
| 图 10 检验点对位置偏差与坡度的关系图 Fig. 10 The relationship between position deviation and terrain slope |
针对当前常用的低潮线提取方法不能适应较大区域范围的现状,提出一种基于曲面求交的低潮线提取方法。通过分析、计算及试验比对,得出如下结论:
(1) 大范围的沿岸区域内,潮汐变化差异可能较大,相比基于简单求交的低潮线提取方法,本文所提方法通过构建曲面形态的沿岸低潮面模型,直接采用曲面求交的方法提取低潮线,能够更充分地顾及大区域内潮汐变化的差异,可以提取精度更高的沿岸低潮线。
(2) 低潮线提取精度与地形坡度有密切关系,相比坡度较大的区域,坡度较小的区域提取的低潮线精度较差。对于地形平坦区域的低潮线提取,需要格外重视沿岸低潮面模型的精度。
当然,本文只选取了一个试验区域的相关数据进行了试验,如何利用更多的数据源来论证沿岸低潮面模型精度对低潮线提取精度的具体影响,有待以后进行。同时,本文在分区构建潮滩DEM和三角网格曲面求交时所涉及的分区数、包围盒层次等参数均采用经验值,如何确定更合理的参数值以提高算法效率,有待于进一步的分析和探索。
| [1] | ZHANG Liang, MA Hongchao, WU Jianwei. Utilization of LiDAR and Tidal Gauge Data for Automatic Extracting High and Low Tide Lines[J]. Journal of Remote Sensing, 2012, 16(2): 405-416. (张良, 马洪超, 邬建伟. 联合机载LiDAR数据和潮汐数据自动提取潮位线[J]. 遥感学报, 2012, 16(2): 405-416.) |
| [2] | PARKER B B. The Difficulties in Measuring a Consistently Defined Shoreline: The Problem of Vertical Referencing[J]. Journal of Coastal Research, 2003, 38(5): 44-56. |
| [3] | United Nations. United Nations Convention on the Law of the Sea[M]. Beijing: Maritime Press,1992. (联合国. 联合国海洋法公约[M]. 北京: 海洋出版社, 1992.) |
| [4] | ZHANG Haiwen, LI Haiqing. Interpretation of “United Nations Convention on the Law of the Sea”.[M]. Beijing: Maritime Press,2006. (张海文, 李海清.《联合国海洋法公约》释义集[M]. 北京: 海洋出版社, 2006.) |
| [5] | PENG Rencan. Research and Practice of Maritime Boundary Delimitation of GIS Technology[D]. Zhengzhou: Information Engineer University, 2003. (彭认灿. 海洋划界GIS技术研究与实践[D]. 郑州: 信息工程大学, 2003.) |
| [6] | FAN Xuewei, GAO Ruiping, ZHANG Hande. Study on Extracting Method of High and Low Water Marks Based on the Imaging Hyperspectral Data[J]. Advances in Marine Science, 2006, 24(4): 561-567. (范学炜, 高瑞萍, 张汉德. 基于成像高光谱数据的高低潮潮位线提取方法研究[J]. 海洋科学进展, 2006, 24(4): 561-567.) |
| [7] | LIU Shanwei, ZHANG Jie, MA Yi, et al. Coastline Extraction Method Based on Remote Sensing and DEM[J]. Remote Sensing Technology and Application, 2011, 26(5): 613-618. (刘善伟, 张杰, 马毅, 等. 遥感与DEM相结合的海岸线高精度提取方法[J]. 遥感技术与应用, 2011, 26(5): 613-618.) |
| [8] | SHEN Fang, GAO Ang, WU Jianping, et al. A Remotely Sensed Approach on Waterline Extraction of Silty Tidal Flat for DEM Construction: A Case Study in Jiuduansha Shoal of Yangtze River[J]. Acta Geodaetica et Cartographica Sinica, 2008, 3(1): 102-107. (沈芳, 郜昂, 吴建平, 等. 淤泥质潮滩水边线提取的遥感研究及DEM构建[J]. 测绘学报, 2008, 3(1): 102-107.) |
| [9] | ZHENG Zongsheng, ZHOU Yunxuan, JIANG Xuezhong, et al. Waterline Extraction and DEM Reconstruction in Chongming Dongtan[J]. Remote Sensing Technology and Application, 2007, 22(1): 35-38. (郑宗生, 周云轩, 蒋雪中,等. 崇明东滩水边线信息提取与潮滩DEM的建立[J]. 遥感技术与应用, 2007, 22(1): 35-38.) |
| [10] | PAJAK M J, LEATHERMAN S. The High Water Line as Shoreline Indicator[J]. Journal of Coastal Research, 2002, 18(2): 329-337. |
| [11] | YAN Haibing, LI Bingbai, CHEN Mingdong. Progress of Researches in Coastline Extraction Based on RS Technique[J]. Areal Research and Development, 2009, 28(1): 101-104. (严海兵, 李秉柏, 陈敏东. 遥感技术提取海岸线的研究进展[J]. 地域研究与开发, 2009, 28(1): 101-104.) |
| [12] | SHEN Jiashuang, ZHAI Jingsheng, GUO Haitao. Study on Coastline Extraction Technology[J]. Hydrographic Surveying and Charting, 2009, 29(6): 72-77. (申家双, 翟京生, 郭海涛. 海岸线提取技术研究[J]. 海洋测绘, 2009, 29(6): 72-77.) |
| [13] | SHEN Jiashuang. Research on Technology of Equal Water Line Information Extraction and Vertical Datum Transforma-tion in Coastal Zone[D]. Zhengzhou: Information Engineer University, 2011. (申家双. 海岸带等水位线信息提取与垂直基准转换技术研究[D]. 郑州: 信息工程大学, 2011.) |
| [14] | LIU H X, SHERMAN D, GU S G. Automated Extraction of Shore-lines from Airborne Light Detection and Ranging Data and Accuracy Assessment Based on Monte Carlo Simulation[J]. Journal of Coastal Research, 2007, 23(6): 1359-1369. |
| [15] | MIRANTE A, WEINGARTEN N. The Radial Sweep Algorithm for Constructing Triangulated Irregular Networks[J]. IEEE Computer Graphics and Applications, 1982, 2(3): 11-21. |
| [16] | XU Qing, CHANG Ge, YANG Li. The Algorithm of TIN Generation Based on Self-adapt Clump Organization[J]. Journal of Image and Graphics, 2000, 5A(6): 461-465. (徐青, 常歌, 杨力. 基于自适应分块的TIN三角网建立算法[J]. 中国图象图形学报, 2000, 5A(6): 461-465.) |
| [17] | HU Jinxing, MA Zhaoting, WU Huanping, et al. Massive Data Delaunary Triangulation Based on Grid Partition Method[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 163-167. (胡金星, 马照亭, 吴焕萍, 等. 基于格网划分的海量Delaunary三角剖分[J]. 测绘学报, 2004, 33(2): 163-167.) |
| [18] | XU Jun, BAO Jingyang, LIU Yanchun, et al. A Regional Tide Model Around China Developed by POM and Blending Assimilation Method[J]. Hydrographic Surveying and Charting, 2008, 28(6): 15-17. (许军, 暴景阳, 刘雁春, 等. 基于POM模式与Blending同化法建立中国近海潮汐模型[J]. 海洋测绘, 2008, 28(6): 15-17.) |
| [19] | HESS K W. Spatial Interpolation of Tidal Data in Irregularly-shape Coastal Regions by Numerical Solution of Laplace’s Equation Estuarine[J]. Coastal and Shelf Science, 2002, 54: 175-192. |
| [20] | JIANG Qianping, TANG Jie, YUAN Chunfeng. Fast Triangle Mesh Surface Intersection Algorithm Based on Uniform Grid[J]. Computer Engineering, 2008, 36(19): 1-3. (蒋钱平, 唐杰, 袁春风. 基于平均单元格的三角网格曲面快速求交算法[J]. 计算机工程, 2008, 36(19): 1-3.) |
| [21] | ZHOU Hai. Research on Modeling Technology of Subdivision Surface[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2004. (周海. 细分曲面造型技术研究[D]. 南京: 南京航空航天大学, 2004.) |